DOCSLIB.ORG

Hydrology, Description of Computer Models, and Evaluation of Selected Water-Management Alternatives in the San Bernardino Area, California

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Hydrology, Description of Computer Models, and Evaluation of Selected Water-Management Alternatives in the San Bernardino Area, California In cooperation with the San Bernardino Valley Municipal Water District Hydrology, Description of Computer Models, and Evaluation of Selected Water-Management Alternatives in the San Bernardino Area, California U.S. Geological Survey Open-File Report 2005-1278 Pending release as USGS Professional Paper 1734 U.S. DEPARTMENT OF THE INTERIOR U.S. GEOLOGICAL SURVEY ountains rdino M erna Seven Oaks n B Y Sa Dam uc aip Crafton a B asin Mill Cr Hills Fault Redlands Andreas River San Zanja San Bernardino Ana Newmark plume Redlands plumeThe Former Santa Muscoy plume (1900) marshland Lytle Creek Cover. Oblique view showing the San Bernardino Mountains rising above the Bunker Hill and Lytle Creek basins. The area simulated with the ground-water flow model is outlined in white. Also shown are selected water-management issues including the former marshland, Seven Oaks Dam, and the Newmark, Muscoy, and Redlands plumes. Hydrology, Description of Computer Models, and Evaluation of Selected Water-Management Alternatives in the San Bernardino Area, California By Wesley R. Danskin, Kelly R. McPherson, and Linda R. Woolfenden In cooperation with the San Bernardino Valley Municipal Water District Open-File Report 2005-1278 Pending release as USGS Professional Paper 1734 U.S. Department of the Interior U.S. Geological Survey U.S. Department of the Interior Dirk Kempthorne, Secretary U.S. Geological Survey Mark D. Myers, Director U.S. Geological Survey, Reston, Virginia: 2006 For product and ordering information: World Wide Web: http://www.usgs.gov/pubprod Telephone: 1-888-ASK-USGS For more information on the USGS—the Federal source for science about the Earth, its natural and living resources, natural hazards, and the environment: World Wide Web: http://www.usgs.gov Telephone: 1-888-ASK-USGS Any use of trade, product, or firm names is for descriptive purposes only and does not imply endorsement by the U.S. Government. Although this report is in the public domain, permission must be secured from the individual copyright owners to reproduce any copyrighted materials contained within this report. Suggested citation: Danskin, W.R., McPherson, K.R., and Woolfenden, L.R., 2006, Hydrology, Description of Computer Models, and Evaluation of Selected Water-Management Alternatives in the San Bernadino Area, California: U.S. Geological Survey Open-File Report 2005-1278, 178 p. and 2 pl. iii Contents Abstract ...........................................................................................................................................................1 Introduction.....................................................................................................................................................3 Purpose and Scope ..............................................................................................................................3 Description of Study Area ...................................................................................................................7 Previous Investigations........................................................................................................................9 Acknowledgments ..............................................................................................................................14 Hydrology ......................................................................................................................................................15 Surface-Water System ......................................................................................................................15 Sources of Inflow and Outflow ................................................................................................19 Gaged Runoff .....................................................................................................................19 Ungaged Runoff ................................................................................................................24 Local Runoff .......................................................................................................................26 Imported Water .................................................................................................................29 Wastewater Discharge ....................................................................................................29 Ground-Water Discharge into Warm Creek .................................................................31 Diversions....................................................................................................................................32 Ground-Water System .......................................................................................................................32 Description of Valley-Fill Aquifer .............................................................................................33 Recharge and Natural Discharge ...........................................................................................35 Recharge from Gaged Streamflow ................................................................................35 Recharge from Ungaged Runoff .....................................................................................39 Recharge from Direct Precipitation ...............................................................................40 Recharge from Local Runoff ...........................................................................................40 Artifical Recharge from Imported Water ......................................................................41 Return Flow from Pumpage .............................................................................................41 Underflow ...........................................................................................................................42 Ground-Water Discharge into Warm Creek .................................................................46 Evapotranspiration. ...................................................................................................................46 Pumpage......................................................................................................................................47 Ground-Water Storage .............................................................................................................52 Ground-Water Budget ...............................................................................................................53 Ground-Water Movement ........................................................................................................56 Ground-Water Quality ...............................................................................................................59 Computer Models.........................................................................................................................................61 Ground-Water Flow Model ................................................................................................................61 Conceptual Model .....................................................................................................................63 Relation to Previous Flow Model ............................................................................................64 Design and Discretization ........................................................................................................64 Aquifer Parameters ...................................................................................................................69 Recharge and Discharge ..........................................................................................................70 Calibration ...................................................................................................................................76 Evaluation ....................................................................................................................................81 iv Sensitivity Analysis ....................................................................................................................81 Use and Limitations ...................................................................................................................82 Constrained Optimization Model ......................................................................................................84 General Characteristics ............................................................................................................85 Representation of the Ground-Water Flow System .............................................................89 Mathematical Form of Objectives and Constraints ..............................................................95 Objective Function ............................................................................................................96 Constraints .........................................................................................................................98 Water Supply and Water Distribution ..................................................................98 Ground-Water Level ................................................................................................98 Ground-Water Quality .............................................................................................99 Economic .................................................................................................................100 Bounds ..............................................................................................................................100
Load more

Recommended publications
  • Property Inventory Data
    Successor Agency to the Redevelopment Agency of the City of San Bernardino Long-Range Property Management Plan September 2015 Amended December 2015 II. Long Range Property Management Plan: Property Inventory Data The Successor Agency has jurisdiction over 230 parcels grouped into 46 sites (the “Properties”), all of which are located within the boundaries of the City and subject to the provisions of the Agency’s Project Area Redevelopment Plans and subsequent mergers and amendment, the Agency’s Five-Year Implementation Plan 2009/2010 through 2013/2014, the City’s General Plan, Municipal Code and land use regulations, and related Specific and Vision Plans. The Property Inventory Matrix is intended to summarize the information included within the site narratives that follow the Property Inventory Matrix within this LRPMP. The Successor Agency has endeavored to ensure that the site narratives illuminate and complement the Property Inventory Matrix and do not contain any contradictory information. However, in the outside event of any contradictions between the Property Inventory Matrix and the site narratives, the Property Inventory Matrix shall govern. Successor Agency: San Bernardino City County: San Bernardino LONG-RANGE PROPERTY MANAGEMENT PLAN: PROPERTY INVENTORY DATA Site Data Property Value/Sale Info Other Property Information HSC § HSC § HSC § HSC § SALE OF PROPERTY HSC § 34191.5 (c) (1) HSC § 34191.5 (c) HSC § 34191.5 (c) (1) (C) HSC § 34191.5 (c) (2) HSC § 34191.5 (c) (1) (A) 34191.5 (c) 34191.5 (c) HSC § 34191.5 (c) (1) (E) 34191.5 (c) 34191.5 (c) (If applicable) (C) (1) (G) (1) (B) (1) (D) (1) (F) (1)H) If Sale of Date of Est’d Prop Property, Value at Estimated Estimate of Acquisition Est’d Current Proposed Proposed Lot Size Current Site No.
    [Show full text]
  • Chapter 3 Watershed Setting
    Chapter 3 Watershed Setting Physical Setting, Hydrology, and Geomorphology Dunne and Leopold (1978) define a watershed as an area of land that drains water, sediment, and dissolved materials to a common outlet at some point along a stream channel. The Santa Ana River Watershed, depicted in Figure 3­1, drains a 2,650 square‐mile area. The watershed is home to over 6 million people and includes the major population centers of parts of Orange, Riverside, and San Bernardino Counties, as well as a sliver of Los Angeles County. The Santa Ana River flows over 100 miles and drains the largest coastal stream system in southern California. It Figure 3­1 discharges into the Pacific Ocean at the City of Santa Ana River Watershed Huntington Beach. The total length of the SAR and its major tributaries is about 700 miles. The watershed boundaries nearly match the boundaries of the Santa Ana Regional Water Quality Control Board, an organization with whom SAWPA has worked closely for many years. In addition, its boundaries match the IRWM region and the recognized Santa Ana Funding Area, as defined by the Proposition 84 IRWM program. Although there are many sub‐watershed planning efforts, OWOW attempts to bring all these efforts, as well as all different jurisdictions in the watershed, into a single watershed‐wide vision. Over the years, SAWPA has participated in the development of sub‐regional IRWM plans, with the understanding that such plans would be complementary to OWOW. Today much of the lower Santa Ana River has lost its historical character. Geologic and Hydrologic Features of the Watershed Much of the movement of materials, energy, and organisms associated with the channel environment and adjoining upland environment depend on the movement of water within the Watershed.
    [Show full text]
  • Shandin Hills Middle School
    Vermont Elementary School 3695 Vermont Street San Bernardino, CA 92407 (909) 880-6658 Fax: (909) 880-1348 Ana Maria Perez, Principal Sarah McCain, Vice Principal OFFICE STAFF Christine Ortega .......................Bil. Secretary II Leticia Salas ..............Bil. Attendance Assistant Middle Miriam Avila .....................................Bil. Clerk II Dorothy Thomas ..........Health Aide/Office Asst. TEACHING STAFF Maurea Williamson ...........................Preschool Michelle Long .................................................3 Bianca Alvarez Bautista ..................................K Nora Mendoza ................................................3 Cecilia Martinez Guzman ...............................K Nancy Reyes ..................................................3 Schools Elizabeth Schrader .........................................K Robyn Rivera ..................................................3 Laura Marruffo .................................K Bilingual Kerri Valenzuela .............................................3 Corrine Delgado .............................................1 Norma Zapata ...................................3 Bilingual Kathleen Guthrie .............................................1 Brigette Gonzales ...........................................4 Karan Kilgore ..................................................1 Tamara Rehberg .............................................4 Amanda Manjarrez .........................................1 Shelly Estrada ..................................4 Bilingual Helen Garcia .....................................1
    [Show full text]
  • San Bernardino County California, U
    ADELANTO CITY SAN BERNARDINO COUNTY CALIFORNIA, U. S. A. San Bernardino County. Condado de San Bernardino Officially the County of San Bernardino, is a county located in the Oficialmente, el Condado de San Bernardino, es un condado ubicado en la southern portion of the U.S. state of California, and is located within the parte sur del estado de California en los Estados Unidos, y se encuentra dentro Inland Empire area. As of the 2010 U.S. Census, the population was del área del Inland Empire. A partir del censo estadounidense de 2010, la 2,035,210, making it the fifth-most populous county in California and the población era de 2.035.210, lo que lo convierte en el quinto condado más 14th-most populous in the United States. The county seat is San Bernardino. poblado de California y el 14º más poblado de los Estados Unidos. La sede del condado es San Bernardino. While included within the Greater Los Angeles area, San Bernardino Si bien se incluye dentro del área metropolitana de Los Ángeles, el County is included in the Riverside–San Bernardino–Ontario metropolitan condado de San Bernardino se incluye en el área estadística metropolitana statistical area (also known as the Inland Empire), as well as the Los Riverside-San Bernardino-Ontario (también conocida como Inland Empire), así Angeles–Long Beach combined statistical area. como el área estadística combinada Los Ángeles-Long Beach. With an area of 20,105 square miles (52,070 km2), San Bernardino Con un área de 20,105 millas cuadradas (52,070 km2), el condado de San County is the largest county in the United States by area, although some of Bernardino es el condado más grande de los Estados Unidos por área, aunque Alaska's boroughs and census areas are larger.
    [Show full text]
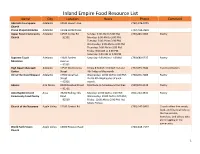
  • Inland Empire Food Resource List
    Inland Empire Food Resource List Name City Location Hours Phone Comment Adelanto Foursquare Adelanto 10931 Lawson Ave (760) 246-8445 Church Praise Chapel Adelanto Adelanto 11328 Bartlett Ave (760) 596-2839 Upper Room Community Adelanto 11555 Cortez Rd Sunday: 9:00 AM to 3:00 PM; (760)246-5066 Pantry Church -- 92301 Monday: 9:00 AM to 3:00 PM; Tuesday: 9:00 AM to 3:00 PM; Wednesday: 9:00 AM to 3:00 PM; Thursday: 9:00 AM to 3:00 PM; Friday: 9:00 AM to 3:00 PM; Saturday: 9:00 AM to 3:00 PM Supreme Touch Adelanto 11833 Barlett Saturday: 9:00AM to 11:00AM (760)680-0537 Pantry Ministries Avenue -- 92301 High Desert Outreach Adelanto 17537 Montezuma Friday 8:30AM-10:00AM 2nd and (760)953-7944 Food Distribution Center Street 4th Friday of the month Christ The Good Shepard Adelanto 17900 Jonathan Wednesday: 10:00 AM to 5:00 PM; (760)246-7083 Pantry Street 2nd & 4th Wednesday of each -- 92301 month. Adonai Alta Noma 8038 Rosebud Street Distribute to homebound families. (909)948-3438 Pantry -- 91701 Anza Baptist Church Anza 39200 Rolling Hills Monday: 10:00 AM to 2:00 PM; (951)763-4937 Pantry Community Food Pantry Road Wednesday: 10:00 AM to 2:00 PM; -- 92539 Friday: 10:00 AM to 2:00 PM; Hot Meals Fridays Church of the Nazarene Apple Valley 12935 Central Rd (760) 247-8433 Church offers free meals, food, and financial help to the low income, homeless, and others who are struggling in the community World Faith Vision Apple Valley 13600 Pawnee Road (760) 813-7177 Church 1 Inland Empire Food Resource List Name City Location Hours Phone Comment Calvary Chapel-Apple Apple Valley 13601 Del Mar Rd.
    [Show full text]
  • 555 East Hospitality Lane San Bernardino, California Capital Markets | National Retail Investment Group Marketed by NRIG-WEST
    OFFERING MEMORANDUM San Bernardino CA RENDERING 555 East Hospitality Lane San Bernardino, California CAPITAL MARKETS | NATIONAL RETAIL INVESTMENT GROUP marketed by NRIG-WEST John Read Brad Rable CBRE-Newport Beach + 1 949 725 8606 + 1 949 725 8468 3501 Jamboree Rd., Ste 100 Lic. 01359444 Lic. 01940290 Newport Beach, CA 92660 [email protected] [email protected] + 1 949 725 8500 www.cbre.com/nrigwest Megan Wood James Slusher + 1 949 725 8423 + 1 949 725 8507 Lic. 01516027 Lic. 01857569 [email protected] [email protected] Philip D. Voorhees + 1 949 725 8521 Lic. 01252096 [email protected] LEASING EXPERT Nelson Wheeler + 1 949 640 6678 Lic. 00781070 [email protected] CONTENTS Investment Highlights Area Overview Property Overview Tenant Overview Financials 1 6 20 24 28 © 2015 CBRE, Inc. The information contained in this document has been obtained from sources believed reliable. While CBRE, Inc. does not doubt its accuracy, CBRE, Inc. has not verified it and makes no guarantee, warranty or representation about it. It is your responsibility to independently confirm its accuracy and completeness. Any projections, opinions, assumptions or estimates used are for example only and do not represent the current or future performance of the property. The value of this transaction to you depends on tax and other factors which should be evaluated by your tax, financial and legal advisors. You and your advisors should conduct a careful, independent investigation of the property to determine to your satisfaction the suitability
    [Show full text]
  • 5. Environmental Analysis
    5. Environmental Analysis 5. ENVIRONMENTAL ANALYSIS 5.1 AESTHETICS Characterizing aesthetics and aesthetic impacts is highly subjective by nature. Aesthetics, as evaluated in this Section of the EIR, involves establishing the existing visual character including visual resources and scenic vistas unique to the City of San Bernardino, the SOI and the Arrowhead Springs area. Visual resources are determined by identifying existing landforms, natural features or urban characteristics; views of sensitive receptors (i.e., residential, schools, recreation areas, etc.); and existing light and glare (i.e., nighttime illumination). The aesthetic impacts of the proposed project are evaluated by determining the aesthetic compatibility of the proposed project with the surrounding area taking into consideration the visual qualities as well as the sensitivity of receptors to these features. 5.1.1 Environmental Setting 5.1.1.1 San Bernardino General Plan Update Visual Character The City of San Bernardino lies on a broad, gently sloping lowland that flanks the southwest margin of the San Bernardino Mountains. The lowland is underlain by alluvial sediments eroded from bedrock in the adjacent mountains and washed by rivers and creeks into the valley region where they have accumulated in layers of gravel, sand, silt and clay. This low lying valley is framed by the San Bernardino Mountains on the northeast and east, Blue Mountains and Box Springs Mountain abutting the Cities of Loma Linda and Redlands to the south, and the San Gabriel Mountains and the Jurupa Hills to the northwest and southwest, respectively. The Santa Ana River has a number of tributaries in the vicinity of San Bernardino that contribute flow to the main stem of the river including Lytle Creek, Cajon Creek, Warm Creek, East Creek and West Twin Creek (see Figure 3.1-2).
    [Show full text]
  • Lawsuit Planned Over Water Release from Seven Oaks Dam Near Highland; Critics Say Santa Ana River Fish Habitat Harmed – Press Enterprise
    Lawsuit planned over water release from Seven Oaks Dam near Highland; critics say Santa Ana River fish habitat harmed – Press Enterprise . LOCAL NEWS Lawsuit planned over water release from Seven Oaks Dam near Highland; critics say Santa Ana River fish habitat harmed https://www.pe.com/...armed/?utm_content=tw-pressenterprise&utm_campaign=socialflow&utm_source=twitter.com&utm_medium=social[12/12/2019 7:54:26 AM] Lawsuit planned over water release from Seven Oaks Dam near Highland; critics say Santa Ana River fish habitat harmed – Press Enterprise Slide gates are lifted below Seven Oaks Dam above Highland on Thursday, May 23, 2019 to allow water to flow into a sedimentation basin. (Photo by Will Lester, Inland Valley Daily Bulletin/SCNG) By CITY NEWS SERVICE | [email protected] | PUBLISHED: December 11, 2019 at 7:46 pm | UPDATED: December 11, 2019 at 7:47 pm Two wildlife advocacy groups Wednesday announced their intent to sue the San Bernardino County Department of Public Works, as well as other regional and federal government agencies, for allegedly putting a fish species’ habitat at risk with the release of water from the Seven Oaks Dam, which the defendants say was necessary to reduce potential public safety hazards. According to the Tucson, Ariz.-based Center for Biological Diversity, the outflows that started on May 11 and continued for several days resulted in high sediment levels that disrupted the spawning activity of Santa Ana sucker fish, which populate the Santa Ana River, coursing through Orange, Riverside S and San Bernardino counties. CBD officials allege foraging grounds were overwhelmed with muck and debris, damaging the https://www.pe.com/...armed/?utm_content=tw-pressenterprise&utm_campaign=socialflow&utm_source=twitter.com&utm_medium=social[12/12/2019 7:54:26 AM] Lawsuit planned over water release from Seven Oaks Dam near Highland; critics say Santa Ana River fish habitat harmed – Press Enterprise sucker’s food supply and smothering fishes’ eggs.
    [Show full text]
  • K-12 Construction Dates
    K-12 Construction Dates 1850s 1960s 1858 Warm Springs Elementary School (1) 1962 Cole Elementary School 1963 Belvedere Elementary School 1880s 1964 San Gorgonio High School 1885 San Bernardino High School (1) 1965 Curtis Middle School 1920s 1965 Lankershim Elementary School 1920 Lincoln Elementary School 1966 Thompson Elementary School 1928 Riley Elementary School 1967 Cajon High School (2) 1924 Cajon High School 1968 Emmerton Elementary School 1929 San Bernardino High School (2) 1968 Kimbark Elementary School 1968 Lincoln Elementary School (2) 1930s 1968 Northpark Elementary School 1935 Alessandro Elementary School 1968 Bonnie Oehl Elementary School 1935 Wilson Elementary School 1968 Riley Elementary School (2) 1936 Marshall Elementary School 1968 Serrano Middle School 1937 Arrowview Middle School 1968 Shandin Hills Middle School 1937 Burbank Elementary School* 1938 Warm Springs Elementary School (2) 1970s 1971 Anderson School 1940s 1971 Carmack School 1943 Bradley Elementary School 1972 Allred Learning Center 1943 Monterey Elementary School 1976 Harmon School 1943 Roosevelt Elementary School 1946 Muscoy Elementary School 1990s 1947 Fairfax Elementary School 1990 North Verdemont Elementary School 1948 Cypress Elementary School 1992 Palm Avenue Elementary School 1948 Del Rosa Elementary School 1994 E. Neal Roberts Elementary School 1949 Davidson Elementary School 2000s 1949 Lytle Creek Elementary School 2000 Arroyo Valley High School 1949 Mount Vernon Elementary School 2005 Anton Elementary School 1949 Newmark Elementary School 2005 Chavez
    [Show full text]
  • VISUAL IMPACT ASSESSMENT I-215/University Parkway Interchange Improvement Project
    VISUAL IMPACT ASSESSMENT I-215/University Parkway Interchange Improvement Project San Bernardino, CA 08-SBd-215-PM 11.35/11.95 EA 0E4200 Project No. 0800000083 January 2019 VISUAL IMPACT ASSESSMENT Interstate‐215/University Parkway Interchange Improvement Project PURPOSE OF STUDY AND ASSESSMENT METHOD The purpose of this visual impact assessment (VIA) is to document potential visual impacts caused by the proposed Project and propose measures to lessen any detrimental impacts that are identified. Visual impacts are demonstrated by identifying visual resources in the project area, measuring the amount of change that would occur as a result of the project, and predicting how the affected public would respond to or perceive those changes. This visual impact assessment follows the guidance outlined in the publication Visual Impact Assessment for Highway Projects published by the Federal Highway Administration (FHWA) in March 1981. PROJECT DESCRIPTION The San Bernardino County Transportation Authority (SBCTA), in cooperation with the California Department of Transportation (Caltrans) and the City of San Bernardino (City), is proposing to improve the Interstate 215 (I‐215)/University Parkway Interchange in the City of San Bernardino, California (Figure 1). Caltrans is the lead agency under the California Environmental Quality Act (CEQA). Caltrans is also the lead agency under the National Environmental Policy Act (NEPA), as assigned by the FHWA, in accordance with NEPA (42 United States Code [USC] 4321 et seq.); and the Council on Environmental Quality (CEQ) Regulations implementing NEPA (40 Code of Federal Regulations [CFR] 1500–1508). A total of two alternatives are being evaluated as part of the I‐215/University Parkway Interchange Improvement Project: Project Alternative 1 (No Build) and Alternative 2 (Diverging Diamond Interchange [DDI]).
    [Show full text]
  • 1.0 Executive Summary
    1.0 EXECUTIVE SUMMARY 1.1 INTRODUCTION This Executive Summary for the Upper Santa Ana River Wash Land Management Plan Environmental Impact Report (EIR) (State of California Clearinghouse No. 2004051023) has been prepared according to California Environmental Quality Act (CEQA) requirements. This EIR has been prepared by LSA Associates, Inc. (LSA) under contract to the San Bernardino Valley Water Conservation District (Lead Agency or District) to identify the proposed project’s potential impacts on the environment, to discuss alternatives, and to propose mitigation measures that will offset, minimize, or otherwise avoid significant environmental impacts. This EIR has been prepared in accordance with CEQA Guidelines Sections 15120 through 15132, 15161, and other applicable sections regulating the preparation of EIRs. 1.2 PROJECT BACKGROUND In 1993, representatives of numerous public and private agencies including Cemex Construction Materials Limited Partnership [LP] (Cemex) and Robertson’s Ready Mix, Ltd. (Robertson’s) formed a Wash Committee to discuss and coordinate proposals for aggregate mining in the Santa Ana River Wash (Wash). As shown in Figure 1.1 (or 3.1) the Wash Area is generally that land area between Greenspot Road on the east, Alabama Street on the west, Greenspot Road and Plunge Creek on the north, and the Santa Ana River on the south. Subsequently, Robertson’s and Cemex forged ahead and submitted applications to mine on Wash lands leased from the San Bernardino Valley Water Conservation District (District). Representatives from the California Department of Fish and Game (CDFG) and U.S. Fish and Wildlife Service (USFWS) had significant issues with the proposals, believing that the land to be mined would significantly disturb important wildlife habitat.
    [Show full text]
  • History of San Bernardino, California, Wikipedia
    History of San Bernardino, California - Wikipedia, the free encyclopedia http://en.wikipedia.org/wiki/History_of_San_Bernardino,_California History of San Bernardino, California From Wikipedia, the free encyclopedia San Bernardino, California, was named in 1810. This article relates to the present-day city of San Bernardino and its surrounding areas. Contents 1 Earliest inhabitants 2 Spanish California 3 Mission California 4 Rancho period 5 Mormon San Bernardino 6 Recall 7 1860s and 1870s 8 Rail wars, rise to local prominence 9 The dawn of the 20th Century 10 World War II and its aftermath 11 Redevelopment and decline 12 Recent history 13 Historical San Bernardino today 14 See also 15 References Earliest inhabitants San Bernardino's earliest known inhabitants were Serrano Indians (Spanish for "people of the mountains") who spent their winters in the valley, and their summers in the cooler mountains. They were known as the "Yuhaviatam" or People of the Pines. They have lived in the valley since approximately 1000 B.C. They lived in small brush covered structures. At the time the Spanish first visited the valley, approximately 1500 Serranos inhabited the area. They lived in villages of ten to thirty structures that the Spanish named rancherías. The Tongva Indians also called the San Bernardino area Wa'aach in their language.[1] Spanish California Spanish Military Commander of California Pedro Fages probably entered San Bernardino valley in 1772. Missionary priest Father Francisco Garces entered the valley in 1774, as did the de Anza Expedition, though not in present-day San Bernardino. The traditional (since there is a dispute as to the following events) founding and naming of San Bernardino is that Padre Francisco Dumetz, a Franciscan priest, made a trip from the Mission San Gabriel Arcángel to the San Bernardino Valley on May 20, 1810, the feast day of Saint Bernardino of Siena (San Bernardino in Spanish) during California's Mission Period.
    [Show full text]