Performance of the STAR Icmi Macroinvertebrate Index and Implications for Classification and Biomonitoring of Rivers
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Tipologia Ente N
07/11/2017 Protocollo Informatico Trentino Tipologia Ente n. Comuni 158 Comunità 15 Pubblica amministrazione locale 10 Società pubbliche strumentali 10 Formazione - Istituti scolastici 76 Musei & Fondazioni 12 Amministrazioni Separate dei beni di Uso 42 Civico (ASUC) Gestioni associate - Unioni 14 Altri Enti 2 TOTALE 339 pag 1 di 12 07/11/2017 Comuni Protocollo Informatico Trentino Comuni Ala Cavizzana Nave San Rocco Stenico Albiano Cembra Lisignago Nogaredo Storo Aldeno Cimone Nomi Strembo Altavalle Cinte Tesino Novaledo Telve Andalo Cis Ossana Telve di Sopra Altopiano della Vigolana Cloz Palù del Fersina Tenna Amblar Don Commezzadura Panchià Tenno Avio Contà Peio Terragnolo Baselga di Pinè Croviana Pellizzano Terzolas Bedollo Daiano Pelugo Tesero Besenello Dambel Pieve di Bono - Prezzo Tione di Trento Bieno Denno Pieve Tesino Ton Bleggio Superiore Dimaro Folgarida Pomarolo Torcegno Bocenago Faedo Porte di Rendena Trambileno Bondone Fai della Paganella Pozza di Fassa Tre Ville Borgo Chiese Fiavè Predaia Trento Borgo Lares Fierozzo Predazzo Valdaone Brentonico Folgaria Primiero San Martino di Castrozza Valfloriana Bresimo Fondo Rabbi Vallarsa Brez Fornace Revò Vallelaghi Caderzone Terme Frassilongo Romallo Varena Cagnò Garniga Terme Romeno Vermiglio Calceranica al Lago Giovo Roncegno Terme Vignola Falesina Caldes Giustino Ronchi Valsugana Vigo di Fassa Caldonazzo Imer Ronzo-Chienis Villa Lagarina Calliano Isera Ronzone Ville d'Anaunia Canazei Lavarone Roverè della Luna Volano Castello-Molina di Fiemme Ledro Ruffrè - Mendola Zambana Comano -

Pay 04.31.00 000 Rsm
Applicativo PAGHE PROJECT Paghe per Aziende, Banche ed Assicurazioni, Enti Pubblici Versione 04.31.00 del 29 Gennaio 2016 Elenco contenuti 1 - Inquadramento territoriale....................................................................................2 Versione 04.31.00 Data rilascio 29/01/2016 Pag. 1 / 3 1 - Inquadramento territoriale 1.1.1 Istituzione di nuovi comuni e comuni estinti dall'01/01/2016 (Da: Dati comuni – Tabelle – Generiche – Inquadramento territoriale) (Da: Dati comuni – Tabelle – ISTAT) Con il presente aggiornamento sono state predisposte le tabelle relative ai nuovi comuni (Città, CAP e ISTAT città) che sostituiscono i comuni estinti (a cui è stato attivato il relativo flag) come da tabella che segue. Elenco nuovi comuni dall'01/01/2016 Elenco comuni estinti sostutuiti dal nuovo comune corrispondente M349 – ALTAVALLE D516 – FAVER E150 – GRAUNO E222 – GRUMES L550 – VALDA M350 – ALTOPIANO DELLA VIGOLANA B078 – BOSENTINO C467 – CENTA SAN NICOLO' L697 – VATTARO L896 – VIGOLO VATTARO M351 – AMBLAR-DON A260 – AMBLAR D336 – DON M352 – BORGO CHIESE B185 – BRIONE C694 – CIMEGO C953 – CONDINO M353 – BORGO LARES A933 – BOLBENO M198 – ZUCLO M354 – CASTEL IVANO I889 – SPERA I979 – STRIGNO L910 – VILLA AGNEDO M355 – CEMBRA LISIGNAGO C452 – CEMBRA E614 – LISIGNAGO M356 – CONTA' D206 – CUNEVO D631 – FLAVON L137 – TERRES M357 – MADRUZZO B386 – CALAVINO E461 – LASINO M358 – PORTE DI RENDENA D250 – DARE' L903 – VIGO RENDENA M006 – VILLA RENDENA M359 – PRIMIERO SAN MARTINO DI CASTROZZA D572 – FIERA DI PRIMIERO I760 – SIROR L201 – TONADICO -

Norme Per La Raccolta Dei Funghi in Provincia Di Trento Comuni Di: Borgo Lares – Tione Di Trento – Tre Ville
NORME PER LA RACCOLTA DEI FUNGHI IN PROVINCIA DI TRENTO COMUNI DI: BORGO LARES – TIONE DI TRENTO – TRE VILLE Legge Provinciale 23 maggio 2007, n. 11; Decreto del Presidente 26 ottobre 2009, n. 23-25/Leg. L.P. 11/2007 Deliberazione della Giunta Provinciale 30 dicembre 2009 ATTENZIONE !!! La raccolta funghi è consentita alle seguenti condizioni: raccolta solo dalle ore 7.00 del mattino alle ore 19.00; quantità massima di 2 chilogrammi al giorno per persona di età superiore ai 10 anni; pulizia sommaria dei funghi sul posto di raccolta; trasporto con contenitori forati e rigidi; divieto di danneggiare o distruggere i funghi sul terreno; divieto di usare rastrelli, uncini ed altri mezzi che possano danneggiare il terreno. pagamento della “tassa raccolta funghi” commisurata al periodo di durata della raccolta (vedi retro) e tenuto conto delle seguenti specificazioni: Agevolazioni Ai soggetti sotto elencati è applicata l’agevolazione del pagamento relativo alla raccolta dei funghi, nella misura del 50 per cento degli importi prestabiliti: a) persone che soggiornano a scopi turistici in un comune della provincia per almeno tre giorni consecutivi (due pernottamenti); b) persone che sono state anagraficamente residenti per almeno cinque anni o hanno un genitore anagraficamente residente in un Comune della Provincia; c) persone che sono titolari di un diritto di proprietà o altro diritto reale su immobili adibiti ad uso abitativo ubicati in uno dei comuni del presente ambito territoriale omogeneo. Esenzioni Sono esentati dall'obbligo della presentazione della denuncia di raccolta funghi e dal pagamento: - i residenti o comunque i nati in un comune della provincia di Trento; - i cittadini iscritti all'anagrafe italiani residenti all'estero (AIRE) dei comuni della Provincia; - i proprietari o i possessori di boschi ricadenti in territorio provinciale, ancorché non residenti in un comune della provincia; - coloro che godono di diritto di uso civico, nell’ambito del territorio di proprietà o gravato dal diritto di uso civico. -

Istituti Scolastici 76
13/07/2021 Protocollo Informatico Trentino Tipologia Ente n. Comuni 151 Comunità 15 Pubblica amministrazione locale 12 Società pubbliche strumentali 13 Formazione - Istituti scolastici 76 Musei & Fondazioni 11 Amministrazioni Separate dei beni di Uso 43 Civico (ASUC) Altri Enti 10 TOTALE 331 pag 1 di 12 13/07/2021 Comuni Protocollo Informatico Trentino Comuni Ala Cavedago Moena Albiano Cavedine Molveno Aldeno Cavizzana Mori Altavalle Cembra Lisignago Nogaredo Altopiano della Vigolana Cimone Nomi Amblar Don Cinte Tesino Novaledo Andalo Cis Novella Avio Comano Terme Ossana Baselga di Pinè Commezzadura Palù del Fersina Bedollo Contà Panchià Besenello Croviana Peio Bieno Dambel Pellizzano Bleggio Superiore Denno Pelugo Bocenago Dimaro Folgarida Pergine Valsugana Bondone Fai della Paganella Pieve di Bono - Prezzo Borgo Chiese Fiavè Pieve Tesino Borgo d'Anaunia Fierozzo Pomarolo Borgo Lares Folgaria Porte di Rendena Brentonico Fornace Predaia Bresimo Frassilongo Predazzo Caderzone Terme Garniga Terme Primiero San Martino di Castrozza Calceranica al Lago Giovo Rabbi Caldes Giustino Riva del Garda Caldonazzo Imer Romeno Calliano Isera Roncegno Terme Campitello di Fassa Lavarone Ronchi Valsugana Campodenno Ledro Ronzo-Chienis Canal San Bovo Livo Ronzone Canazei Lona - Lases Roverè della Luna Capriana Luserna Ruffrè - Mendola Carisolo Madruzzo Rumo Carzano Malè Sagnon - Mis Castel Condino Massimeno Samone Castello-Molina di Fiemme Mazzin San Giovanni di Fassa - Sen Jan Castello Tesino Mezzana San Lorenzo Dorsino Castelnuovo Mezzano San Michele all'Adige -

Tabella Degli Enti (Comuni O Province) Che Riscuotono Alcuni Tributi Tramite
Tabella aggiornata al 05 dicembre 2019 Tabella degli enti (comuni o province) che riscuotono alcuni tributi tramite modello F24 IMIS, TARSU/TARIFFA, TOSAP/COSAP, imposta di scopo (ISOP), tassa/contributo di soggiorno (TDS) AVVERTENZA: la presente tabella indica esclusivamente per quali enti è possibile pagare alcuni tributi tramite modello F24. Per informazioni e chiarimenti sulla disciplina dei tributi, sul presupposto, sulle aliquote e annualità per le quali gli stessi sono dovuti (ad esempio, per l'imposta di scopo), è necessario rivolgersi ai singoli enti. CODICE CODICE DATA ATTIVAZIONE DENOMINAZIONE ENTE (Comune o Provincia, identificati dal ENTE TRIBUTO (AAAA/MM/GG) TIPO TRIBUTO codice catastale o dalla sigla automobilistica) A091 3936 2018/10/10 TDS AGROPOLI A091 3937 2018/10/10 TDS AGROPOLI A091 3938 2018/10/10 TDS AGROPOLI A116 3990 2015/06/01 IMIS ALA A116 3991 2015/06/01 IMIS ALA A116 3992 2015/06/01 IMIS ALA A116 3993 2015/06/01 IMIS ALA A116 3994 2015/06/01 IMIS ALA A116 3995 2015/06/01 IMIS ALA A116 3996 2015/06/01 IMIS ALA A121 3936 2018/07/03 TDS ALANO DI PIAVE A121 3937 2018/07/03 TDS ALANO DI PIAVE A121 3938 2018/07/03 TDS ALANO DI PIAVE A158 3990 2015/06/01 IMIS ALBIANO A158 3991 2015/06/01 IMIS ALBIANO A158 3992 2015/06/01 IMIS ALBIANO A158 3993 2015/06/01 IMIS ALBIANO A158 3994 2015/06/01 IMIS ALBIANO A158 3995 2015/06/01 IMIS ALBIANO A158 3996 2015/06/01 IMIS ALBIANO A178 3990 2015/06/01 IMIS ALDENO A178 3991 2015/06/01 IMIS ALDENO A178 3992 2015/06/01 IMIS ALDENO A178 3993 2015/06/01 IMIS ALDENO A178 3994 2015/06/01 -

L'animazione ESTIVA Per Bambini E Ragazzi Dal 3° Anno Della Scuola Dell’Infanzia Alla 2° Superiore 8
L'ANIMAZIONE ESTIVA per bambini e ragazzi dal 3° anno della scuola dell’infanzia alla 2° superiore 8 Attività organizzate da ASD Virtus Giudicariese e L’Ancora s.c.s. NLUS O società cooperativa sociale 1 BENVENUTI A 8 L’ASD Virtus Giudicariese e L’Ancora s.c.s. organizzano emozionanti settimane scandite da sport, attività ludico-educative e gite per bambini e ragazzi, residenti e ospiti, nei comuni della Busa di Tione e della Val Rendena. ATTIVITÀ Virtuo…samente KIDS Destinatari: i bambini dal terzo anno della scuola dell’infanzia (2012) alla prima media (2006) NB: Possibilità di inserimento anche dei bambini che anticiperanno l’ingresso a scuola (2013) Possibilità di inserimento dei ragazzi di prima media (2006) su richiesta nelle settimane TEEN Periodo: dal 18 giugno al 31 agosto 2018 (esclusa la settimana dal 13 al 17 agosto) Organizzazione settimanale e orari: LUNEDÌ E mARTEDÌ MERCOLEDÌ GIOVEDÌ E VENERDÌ 08:00-12:30 Attività sportive Uscita in Territorio Attività sportive 12:30-14:00 Pranzo (facoltativo) Pranzo Pranzo (facoltativo) 14:00-18:00 Attività ludico-educative Uscita in Territorio Attività ludico-educative Iscrizione: obbligatoria per un minimo di tre settimane, anche non consecutive PROGRAmmAzIONE: ATTIVITÀ SPORTIVE – VIRTUS Gli sport proposti sono: acrobatica, skateboard, baseball, nuoto, arrampicata, roller, basket, atletica, monopattino, calcio, orienteering, monociclo, criket, tiro con l’arco, bmx, golf, pingpong, kart (pedali), hockey, tennis, pallamano, badminton, rugby, volley. Proposti tenendo presente le caratteristiche evolutive dei ragazzi, in un percorso dal globale all’analitico, con incentivo alla socializzazione e all’aggregazione. Per i più piccoli, giochi sportivi finalizzati: alla strutturazione degli schemi motori di base, al miglioramento dello schema corporeo e stimolare il senso di collaborazione, condivisione e socializzazione. -

Progetto Banda Ultra Larga in Trentino
PROGETTO BANDA ULTRA LARGA IN TRENTINO La colonna “DATA INIZIO LAVORI PRESUNTA” riporta la data di inizio lavori presunta stimata da Open Fiber sulla base delle tempistiche necessarie per lo svolgimento delle attività di progettazione definitiva ed esecutiva, di approvazione dei progetti e per l'ottenimento dei permessi da parte dei Comuni. Tabella aggiornata al 1 marzo 2019 (1) = Open Fiber non ha ancora definito e comunicato una data di inizio lavori COMUNE 2014 ISTAT COMUNE 2017 ISTAT DATA INIZIO 2014 2017 LAVORI PRESUNTA Ala 22001 giugno 2019 Albiano 22002 (1) Aldeno 22003 (1) Amblar 22004 Amblar-Don 22237 (1) Andalo 22005 (1) Arco 22006 settembre 2018 Avio 22007 maggio 2019 Baselga di Pinè 22009 (1) Bedollo 22011 (1) Bersone 22012 Valdaone 22232 (1) Besenello 22013 (1) Bieno 22015 (1) Bleggio Superiore 22017 ottobre 2019 Bocenago 22018 ottobre 2019 Bolbeno 22019 Borgo Lares 22239 (1) Bondo 22020 Sella Giudicarie 22246 (1) Bondone 22021 ottobre 2019 Borgo Valsugana 22022 (1) Bosentino 22023 Altopiano della Vigolana 22236 (1) Breguzzo 22024 Sella Giudicarie 22246 (1) Brentonico 22025 ottobre 2019 Bresimo 22026 (1) Brez 22027 (1) Brione 22028 Borgo Chiese 22238 (1) Caderzone Terme 22029 (1) Cagnò 22030 (1) Calavino 22031 Madruzzo 22243 giugno 2019 Calceranica al Lago 22032 maggio 2019 Caldes 22033 (1) Caldonazzo 22034 ottobre 2019 Calliano 22035 (1) Campitello di Fassa 22036 (1) Campodenno 22037 (1) Canal San Bovo 22038 (1) Canazei 22039 (1) Capriana 22040 (1) Carano 22041 (1) Carisolo 22042 agosto 2018 Carzano 22043 ottobre 2019 Castel -

Avviso Aggiudicazione
PAT/RFS171-29/10/2019-0668659 - Allegato Utente 1 (A01) AVVISO DI AGGIUDICAZIONE AI SENSI ART. 28 L.P. 26/93 1. AMMINISTRAZIONE AGGIUDICATRICE: Provincia Autonoma di Trento – Agenzia Provinciale per gli Appalti e Contratti – Servizio appalti – Ufficio procedure telematiche di lavori pubblici – Via Dogana, 8 – 38122 – TRENTO. 2. PROCEDURA DI AGGIUDICAZIONE: procedura negoziata ai sensi dell’art. 33, comma 5 della L.P. 26/1993. 3. DATA DI AGGIUDICAZIONE DELL’APPALTO: 30 agosto 2019. 4. CRITERIO DI AGGIUDICAZIONE: criterio del prezzo più basso determinato mediante offerta a prezzi unitari ai sensi dell’art. 16, comma 3 della L.P. 2/2016. 5. NUMERO OFFERTE RICEVUTE: 7. 6. AGGIUDICATARIA: A.T.I. COSTRUZIONI I.C.E.S. SRL con sede in Spormaggiore (TN), Via Trento, 7 – GEOTRENTINA SRL con sede in Borgo Valsugana (TN), Via Mercato, 9. 7. OGGETTO DELL’APPALTO: AFFIDAMENTO DEI LAVORI DI “COSTRUZIONE DEL COLLETTORE INTERCOMUNALE DI FOGNATURA NERA CASTELFONDO, BREZ, CLOZ E DAMBEL: TRATTO DI CASTELFONDO – LOTTO 1: EDIFICIO DELLA VASCA IMHOFF.” per l'importo a base d'appalto di € 452.000,00.=. 8. IMPORTO DI AGGIUDICAZIONE: ribasso percentuale del 23,786% (ventitre virgola settecentottantasei per cento) pari ad € 350.991,57.= comprensivo degli oneri per la sicurezza. 9. Il subappalto sarà consentito per i lavori che l’aggiudicataria ha espressamente indicato in sede di offerta, nei limiti di legge. 10. IMPRESE INVITATE ALLA GARA: 1) COSTRUZIONI I.C.E.S. SRL di Spormaggiore (TN) (partecipa alla gara in associazione temporanea con l'impresa GEOTRENTINA SRL di Borgo Valsugana (TN); 2) CO.GI. SARL di Salorno (BZ) (partecipa alla gara in associazione temporanea con l'impresa REGGELBERGBAU di Nova Ponente (BZ); 3) MAK COSTRUZIONI SRL di Lavis (TN) (partecipa alla gara in associazione temporanea con l'impresa DELTA PERFORAZIONI ROCCE SAS di Lavis (TN); 4) EURO SCAVI SRL di Lavis (TN) (partecipa alla gara in associazione temporanea con l'impresa G.T.E. -

Tipologia Ente N. Comuni 158 Comunità 15 Pubblica Amministrazione Locale 10 Società Pubbliche Strumentali 14 Formazione
30/04/2019 Protocollo Informatico Trentino Tipologia Ente n. Comuni 158 Comunità 15 Pubblica amministrazione locale 10 Società pubbliche strumentali 14 Formazione - Istituti scolastici 74 Musei & Fondazioni 11 Amministrazioni Separate dei beni di Uso 43 Civico (ASUC) Altri Enti 5 TOTALE 330 pag 1 di 10 30/04/2019 Comuni Protocollo Informatico Trentino Comuni Ala Cavizzana Nogaredo Sporminore Albiano Cembra Lisignago Nomi Stenico Aldeno Cimone Novaledo Storo Altavalle Cinte Tesino Ossana Strembo Andalo Cis Palù del Fersina Telve Altopiano della Vigolana Cloz Panchià Telve di Sopra Amblar Don Commezzadura Peio Tenna Avio Contà Pellizzano Tenno Baselga di Pinè Croviana Pelugo Terragnolo Bedollo Daiano Pieve di Bono - Prezzo Terre d'Adige Besenello Dambel Pieve Tesino Terzolas Bieno Denno Pomarolo Tesero Bleggio Superiore Dimaro Folgarida Porte di Rendena Tione di Trento Bocenago Faedo Predaia Ton Bondone Fai della Paganella Predazzo Torcegno Borgo Chiese Fiavè Primiero San Martino di Castrozza Trambileno Borgo Lares Fierozzo Rabbi Tre Ville Brentonico Folgaria Revò Trento Bresimo Fondo Riva del Garda Valdaone Brez Fornace Romallo Valfloriana Caderzone Terme Frassilongo Romeno Vallarsa Cagnò Garniga Terme Roncegno Terme Vallelaghi Calceranica al Lago Giovo Ronchi Valsugana Varena Caldes Giustino Ronzo-Chienis Vermiglio Caldonazzo Imer Ronzone Vignola Falesina Calliano Isera Roverè della Luna Villa Lagarina Canazei Lavarone Ruffrè - Mendola Ville d'Anaunia Castello-Molina di Fiemme Ledro Rumo Volano Comano Terme Livo Sagnon - Mis Ziano di Fiemme -

Enti Attivi Aderenti Al Servizio
04/01/2019 Protocollo Informatico Trentino Tipologia Ente n. Comuni 158 Comunità 15 Pubblica amministrazione locale 10 Società pubbliche strumentali 14 Formazione - Istituti scolastici 74 Musei & Fondazioni 11 Amministrazioni Separate dei beni di Uso 43 Civico (ASUC) Altri Enti 5 TOTALE 330 pag 1 di 10 04/01/2019 Comuni Protocollo Informatico Trentino Comuni Ala Cavizzana Nave San Rocco Sporminore Albiano Cembra Lisignago Nogaredo Stenico Aldeno Cimone Nomi Storo Altavalle Cinte Tesino Novaledo Strembo Andalo Cis Ossana Telve Altopiano della Vigolana Cloz Palù del Fersina Telve di Sopra Amblar Don Commezzadura Panchià Tenna Avio Contà Peio Tenno Baselga di Pinè Croviana Pellizzano Terragnolo Bedollo Daiano Pelugo Terzolas Besenello Dambel Pieve di Bono - Prezzo Tesero Bieno Denno Pieve Tesino Tione di Trento Bleggio Superiore Dimaro Folgarida Pomarolo Ton Bocenago Faedo Porte di Rendena Torcegno Bondone Fai della Paganella Predaia Trambileno Borgo Chiese Fiavè Predazzo Tre Ville Borgo Lares Fierozzo Primiero San Martino di Castrozza Trento Brentonico Folgaria Rabbi Valdaone Bresimo Fondo Revò Valfloriana Brez Fornace Romallo Vallarsa Caderzone Terme Frassilongo Romeno Vallelaghi Cagnò Garniga Terme Roncegno Terme Varena Calceranica al Lago Giovo Ronchi Valsugana Vermiglio Caldes Giustino Ronzo-Chienis Vignola Falesina Caldonazzo Imer Ronzone Villa Lagarina Calliano Isera Roverè della Luna Ville d'Anaunia Canazei Lavarone Ruffrè - Mendola Volano Castello-Molina di Fiemme Ledro Rumo Zambana Comano Terme Livo Sagnon - Mis Ziano di Fiemme -
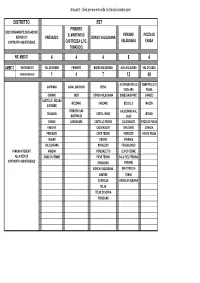
SCHEMA RIORGANIZZAZIONE C a Versione Definitiva
Allegato1 - Sedi permanenti della Continuità assistenziale DISTRETTO EST PRIMIERO SEDE PERMANENTE EROGAZIONE S. MARTINO DI PERGINE POZZA DI SERVIZIO DI PREDAZZO BORGO VALSUGANA CONTINUITA' ASSISTENZIALE CASTROZZA (LOC. VALSUGANA FASSA TONADICO) NR. MEDICI 4 4 4 8 4 AMBITO GEOGRAFICO VAL DI FIEMME PRIMIERO BASSA VALSUGANA ALTA VALSUGNA VAL DI FASSA Ambito Numero 1 4 7 12 49 ALTOPIANO DELLA CAMPITELLO DI CAPRIANA CANAL SAN BOVO BIENO VIGOLANA FASSA CARANO IMER BORGO VALSUGANA BASELGA DI PINE' CANAZEI CASTELLO - MOLINA MEZZANO CARZANO BEDOLLO MAZZIN DI FIEMME PRIMIERO SAN CALCERANICA AL CAVALESE CASTEL IVANO MOENA MARTINO DI LAGO DAIANO SAGRON MIS CASTELLO TESINO CALDONAZZO POZZA DI FASSA PANCHIA' CASTENUOVO CIVEZZANO SORAGA PREDAZZO CINTE TESINO FIEROZZO VIGO DI FASSA TESERO GRIGNO FORNACE VALFLORIANA NOVALEDO FRASSILONGO COMUNI AFFERENTI VARENA OSPEDALETTO LEVICO TERME ALLA SEDE DI ZIANO DI FIEMME PIEVE TESINO PALU' DEL FERSINA CONTINUITA' ASSISTENZIALE RONCENGO PERGINE RONCHI VALSUGANA SANT'ORSOLAVALSUGANA SAMONETERME TENNA SCURELLE VIGNOLA-FALESINA TELVE TELVE DI SOPRA TORCEGNO Allegato1 - Sedi permanenti della Continuità assistenziale DISTRETTO OVEST SEDE PERMANENTE EROGAZIONE CEMBA- SERVIZIO DI LISIGNAGO MEZZOLOMBARDO TAIO FONDO PELLIZZANO CONTINUITA' ASSISTENZIALE (LOC. CEMBRA) NR. MEDICI 4 4 4 4 4 AMBITO GEOGRAFICO ROTALIANA, PAGANELLA, VAL DI CEMBRA VAL DI NON VAL DI SOLE Ambito Numero 16 19 24 25 30 ALBIANO ANDALO CLES AMBLAR-DON CALDES ALTA VALLE CAMPODENNO CONTA' BRESIMO CAVIZZANA COMMEZZADUR CEMBRA-LISIGNAGO CAVEDAGO DENNO BREZ -

Aree Critiche in Media E Bassa Tensione
DELIBERA AEEG 125/10 Allegato A - art. 4.2 comma C Aree critiche in media e bassa tensione CAMPITELLO DI FASSA CAMPITELLO DI FASSA BORGO D'ANAUNIA MAZZIN BORGO D'ANAUNIA CANAZEI RONZONE RUMO NOVELLA BORGO D'ANAUNIA BORGO D'ANAUNIA SAN GIOVANNI DI FASSA-SEN JAN RONZONERUFFRE'-MENDOLA SAN GIOVANNI DI FASSA-SEN JAN LIVO NOVELLA BRESIMO SARNONICO SAN GIOVANNI DI FASSA-SEN JAN CAVARENO NOVELLA SORAGA SORAGA RABBI DAMBEL CIS NOVELLANOVELLA AMBLAR-DON ROMENO CALDES AMBLAR-DON MOENA SANZENO PEIO CAVIZZANA TERZOLAS PREDAIA PREDAZZO MALE' CLES PELLIZZANO PREDAIA SFRUZ PREDAZZO VILLE D'ANAUNIA VILLE DI FIEMME VILLE D'ANAUNIA PREDAIA CROVIANA PRIMIERO SAN MARTINO DI CASTROZZA MEZZANA PREDAIA DIMARO FOLGARIDA VILLE DI FIEMME VILLE D'ANAUNIA PREDAZZO COMMEZZADURA VILLE D'ANAUNIA CONTA' PREDAIA VILLE DI FIEMME PELLIZZANO PREDAIA CONTA' TESERO DIMARO FOLGARIDA CONTA' ZIANO DI FIEMME CAPRIANA DENNO VERMIGLIO TON PRIMIERO SAN MARTINO DI CASTROZZA VILLE D'ANAUNIA ROVERE' DELLA LUNA PANCHIA' OSSANA CAVALESE CAMPODENNO ALTAVALLE PRIMIERO SAN MARTINO DI CASTROZZA IMER MEZZOCORONA ALTAVALLE CASTELLO-MOLINA DI FIEMME VALFLORIANA CARISOLO SPORMINORE MEZZOCORONA SOVER CANAL SAN BOVO PINZOLO ALTAVALLE SAN MICHELE ALL'ADIGE CANAL SAN BOVO SAGRON MIS MEZZOLOMBARDO ALTAVALLE TRE VILLE LONA-LASES PIEVE TESINO SPORMAGGIORE SEGONZANO PRIMIERO SAN MARTINO DI CASTROZZA SAN MICHELE ALL'ADIGE GIUSTINO CEMBRA LISIGNAGO PRIMIERO SAN MARTINO DI CASTROZZA SPIAZZO CAVEDAGO GIOVO STREMBO CARISOLO FAI DELLA PAGANELLA CEMBRA LISIGNAGO BASELGA DI PINE' TERRE D'ADIGE BEDOLLO ANDALO