Planning Skip-Stop Transit Service Under Heterogeneous Demands
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Union Station Conceptual Engineering Study
Portland Union Station Multimodal Conceptual Engineering Study Submitted to Portland Bureau of Transportation by IBI Group with LTK Engineering June 2009 This study is partially funded by the US Department of Transportation, Federal Transit Administration. IBI GROUP PORtlAND UNION STATION MultIMODAL CONceptuAL ENGINeeRING StuDY IBI Group is a multi-disciplinary consulting organization offering services in four areas of practice: Urban Land, Facilities, Transportation and Systems. We provide services from offices located strategically across the United States, Canada, Europe, the Middle East and Asia. JUNE 2009 www.ibigroup.com ii Table of Contents Executive Summary .................................................................................... ES-1 Chapter 1: Introduction .....................................................................................1 Introduction 1 Study Purpose 2 Previous Planning Efforts 2 Study Participants 2 Study Methodology 4 Chapter 2: Existing Conditions .........................................................................6 History and Character 6 Uses and Layout 7 Physical Conditions 9 Neighborhood 10 Transportation Conditions 14 Street Classification 24 Chapter 3: Future Transportation Conditions .................................................25 Introduction 25 Intercity Rail Requirements 26 Freight Railroad Requirements 28 Future Track Utilization at Portland Union Station 29 Terminal Capacity Requirements 31 Penetration of Local Transit into Union Station 37 Transit on Union Station Tracks -

Trimet SE Service Enhancement Plan
Presentation to the Clackamas County Board of County Commissioners September 22, 2015 Schedule Westside: Completed in 2014 Southwest: Completed in 2015 Eastside: Completion in 2016 Southeast: Completion in 2016 North/Central: Completion in 2016 Annual Service Plan Optimize & Maintain Restore Increase Capacity & Restore Frequent Increase spans & Reliability Service Levels frequencies Schedule & detail Add new lines tweaks Optimize routes & schedules Reconfigure lines Hillsboro Beaverton Gresham Portland Forest Grove/ Cornelius Tigard Happy Milwaukie King Valley City Lake Oswego Tualatin Legend Sherwood West Job center Linn Oregon City Downtown trips Hillsboro Beaverton Gresham Portland Forest Grove/ Cornelius Tigard Happy Milwaukie King Valley City Lake Oswego Tualatin Legend Sherwood West Job center Linn Oregon City Downtown trips Hillsboro Beaverton Gresham Portland Forest Grove/ Cornelius Tigard Happy Milwaukie King Valley City Lake Oswego Legend Tualatin Sherwood West Job center Linn Oregon City Downtown trips Outreach efforts: More service to Sunnyside Rd. Clackamas Industrial Area OC to Tualatin service Service to S. Oregon City trimet.org/southeast SOUTHEAST Help make transit better in your community Making Transit Better in Southeast Draft Vision We’ve been talking with riders What we heard from the community and community members We learned from Southeast riders and residents about the about improving bus service in challenges they face today and how the region will grow in the future. Based on this, we’re proposing more and better Southeast Portland, Estacada, bus service to help people get to jobs, education, health Gladstone, Happy Valley, care, affordable housing and essential services. Proposed Milwaukie, Oregon City and bus service improvements include route changes and extensions, new bus lines, adjusted frequency and better Clackamas County. -

Coordinated Transportation Plan for Seniors and Persons with Disabilities I Table of Contents June 2020
Table of Contents June 2020 Table of Contents 1. Introduction .................................................................................................... 1-1 Development of the CTP .......................................................................................................... 1-3 Principles of the CTP ................................................................................................................ 1-5 Overview of relevant grant programs ..................................................................................... 1-7 TriMet Role as the Special Transportation Fund Agency ........................................................ 1-8 Other State Funding ................................................................................................................. 1-9 Coordination with Metro and Joint Policy Advisory Committee (JPACT) .............................. 1-11 2. Existing Transportation Services ...................................................................... 2-1 Regional Transit Service Providers .......................................................................................... 2-6 Community-Based Transit Providers ..................................................................................... 2-18 Statewide Transit Providers ................................................................................................... 2-26 3. Service Guidelines ........................................................................................... 3-1 History ..................................................................................................................................... -

Portland-Milwaukie Light Rail Project Profile, Oregon
Portland-Milwaukie Light Rail Project Portland, Oregon (January 2015) The Tri-County Metropolitan Transportation District of Oregon (TriMet) is constructing a double-track light rail transit (LRT) extension of the existing Yellow Line from the downtown Portland transit mall across the Willamette River, to southeast Portland, the city of Milwaukie, and urbanized areas of Clackamas County. The project includes construction of a new multimodal bridge across the Willamette River, one surface park-and ride lot facility with 320 spaces, one park-and-ride garage with 355 spaces, expansion of an existing maintenance facility, bike and pedestrian improvements and the acquisition of 18 light rail vehicles. Service will operate at 10-minute peak period frequencies during peak periods on weekdays. The project is expected to serve 22,800 average weekday trips in 2030. The project will increase transit access to and from employment and activity centers along the Portland and Milwaukie transportation corridor. It will link Downtown Portland with educational institutions, dense urban neighborhoods, and emerging growth areas in East Portland and Milwaukie. The Willamette River separates most of the corridor from Downtown Portland and the South Waterfront. The corridor’s only north-south highway (Highway 99E), which provides access to Downtown Portland via the existing Ross Island, Hawthorne, Morrison, and Burnside bridges, is limited to two through-lanes in each direction for much of the segment between Milwaukie and central Portland, most of which is congested. Existing buses have slow operating speeds due to congestion, narrow clearances and frequent bridge lift span openings. None of the existing river crossings provide easy access to key markets. -

MAKING HISTORY 50 Years of Trimet and Transit in the Portland Region MAKING HISTORY
MAKING HISTORY 50 Years of TriMet and Transit in the Portland Region MAKING HISTORY 50 YEARS OF TRIMET AND TRANSIT IN THE PORTLAND REGION CONTENTS Foreword: 50 Years of Transit Creating Livable Communities . 1 Setting the Stage for Doing Things Differently . 2 Portland, Oregon’s Legacy of Transit . 4 Beginnings ............................................................................4 Twentieth Century .....................................................................6 Transit’s Decline. 8 Bucking National Trends in the Dynamic 1970s . 11 New Institutions for a New Vision .......................................................12 TriMet Is Born .........................................................................14 Shifting Gears .........................................................................17 The Freeway Revolt ....................................................................18 Sidebar: The TriMet and City of Portland Partnership .......................................19 TriMet Turbulence .....................................................................22 Setting a Course . 24 Capital Program ......................................................................25 Sidebar: TriMet Early Years and the Mount Hood Freeway ...................................29 The Banfield Project ...................................................................30 Sidebar: The Transportation Managers Advisory Committee ................................34 Sidebar: Return to Sender ..............................................................36 -

Transit Technical Report for the Final Environmental Impact Statement
I N T E R S TAT E 5 C O L U M B I A R I V E R C ROSSING Transit Technical Report for the Final Environmental Impact Statement December 2010 Title VI The Columbia River Crossing project team ensures full compliance with Title VI of the Civil Rights Act of 1964 by prohibiting discrimination against any person on the basis of race, color, national origin or sex in the provision of benefits and services resulting from its federally assisted programs and activities. For questions regarding WSDOT’s Title VI Program, you may contact the Department’s Title VI Coordinator at (360) 705-7098. For questions regarding ODOT’s Title VI Program, you may contact the Department’s Civil Rights Office at (503) 986- 4350. Americans with Disabilities Act (ADA) Information If you would like copies of this document in an alternative format, please call the Columbia River Crossing (CRC) project office at (360) 737-2726 or (503) 256-2726. Persons who are deaf or hard of hearing may contact the CRC project through the Telecommunications Relay Service by dialing 7-1-1. ¿Habla usted español? La informacion en esta publicación se puede traducir para usted. Para solicitar los servicios de traducción favor de llamar al (503) 731-4128. Cover Sheet Transit Technical Report Columbia River Crossing Submitted By: Elizabeth Mros-O’Hara, AICP Kelly Betteridge Theodore Stonecliffe, P.E. This page left blank intentionally. Interstate 5 Columbia River Crossing i Transit Technical Report for the Final Environmental Impact Statement TABLE OF CONTENTS 1. INTRODUCTION ..................................................................................................................................... 1-1 1.1 Background .................................................................................................................................................. -

Southwest-Final-Report.Pdf
SOUTHWEST Service Enhancement Plan Final Report December 2015 Dear Reader, I am proud to present the Southwest Service Enhancement Plan, with recommendations to get you and your fellow community members where you need to go. This report provides a vision for future TriMet service in the Southwest portion of the region (for other areas, see www.trimet.org/future). The vision for future service in the Southwest Service Enhancement Plan is the culmination of many hours of meetings with our customers, neighborhood groups, employers, social service providers, educational institutions and stakeholders. Community members provided input through open house meetings, surveys, focus groups, and individual discussions. Extra effort was put into getting input from the entire community, especially youth, seniors, minorities, people with low incomes, and non-English speakers. Demographic research was used to map common trips, and cities and counties provided input on future growth areas. Lastly, TriMet staff coordinated closely with Metro’s South- west Corridor Plan process to ensure that both efforts complement one A note from another and expand transit in the southwest part of our region. TriMet The final result is a plan that calls for bus service that connects people to more places, more often, earlier, and later. The plan also recommends GeneralManager, improvements to the sidewalks and street crossings to support transit service and new community-job shuttles to serve areas that lack transit service because the demand is too low for traditional TriMet service to Neil McFarlane be economically viable. The service enhancement plans are not just visions of the future, but commitments to grow TriMet’s system. -

Transport Regional Its Architecture and Operational Concept Report
Regional ITS Architecture & Operational Concept Plan for the Portland Metro Region prepared for Oregon Department TransPort of Transportation INTERSTATE 5 Clark County Vancouver INTERSTATE 205 Banks North Plains Camas Multnomah County Washougal Maywood Park INTERSTATE 26 84 Fairview INTERSTATE 405 Wood Troutdale Forest Hillsboro Village Grove Cornelius Portland Gresham Beaverton 217 INTERSTATE Washington County 5 Milwaukie Happy Valley Gaston Tigard Lake Oswego Johnson King City City Durham Sandy Gladstone Rivergrove Tualatin West INTERSTATE Linn 205 Sherwood Clackamas County Oregon City Yamhill County Wilsonville Newberg Carlton Estacada Dundee INTERSTATE 5 Canby Barlow Lafayette Dayton prepared by December 2016 TRANSPORT REGIONAL ITS ARCHITECTURE AND OPERATIONAL CONCEPT REPORT ACKNOWLEDGMENTS Metro Project Manager Chris Myers Metro TransPort Committee Jabra Khasho City of Beaverton Aszita Mansor City of Beaverton Tina Nguyen City of Beaverton Jim Gelhar City of Gresham Dan Hazel City of Hillsboro Tegan Enloe City of Hillsboro Amanda Owings City of Lake Oswego Willie Rotich City of Portland Peter Koonce City of Portland Mike Ward City of Wilsonville Bikram Raghubansh Clackamas County Nathaniel Price Federal Highway Administration Caleb Winter Metro Andrew Dick Oregon Department of Transportation Kate Freitag Oregon Department of Transportation Galen McGill Oregon Department of Transportation Dennis Mitchell Oregon Department of Transportation Kristin Tufte Portland State University Mike Coleman Port of Portland Phil Healy Port of Portland -

Facts About Trimet
Facts about TriMet Ridership TriMet is a national leader in providing transit service. TriMet carries more people than nearly every other U.S. transit system its size. Weekly ridership on buses and MAX has increased for all but one year in the past 23 years. TriMet ridership has outpaced population growth and daily vehicle miles traveled for more than a decade. During fiscal year 2011 Residents and visitors boarded a bus, MAX or WES train 100 million times: • 58.4 million were bus trips • 41.2 million were MAX trips • 370,800 were WES trips TriMet’s service area covers 570 square miles within the tri-county region with a Weekday boardings averaged population of 1.5 million people. 318,500 trips: • 190,300 were bus trips Portland is the 24th-largest metro easing traffic congestion and helping • 126,800 were MAX trips area in the U.S., but transit ridership keep our air clean. That adds up to • 1,450 were WES trips is 7th per capita. 28.6 million fewer car trips each year. Weekend ridership: More people ride TriMet than transit TriMet’s MAX and buses combined systems in larger cities, such as eliminate 207,300 daily car trips, or • Bus and MAX ridership averaged Dallas, Denver and San Diego. 65 million trips each year. 343,900 trips. For each mile taken on TriMet, 53% Maintaining livability less carbon is emitted compared to Easing traffic congestion driving alone. MAX carries 26% of evening rush- Annual Ridership Growth Bus, MAX & WES hour commuters traveling from 105 downtown on the Sunset Hwy. -
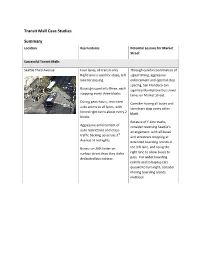
Transit Mall Case Studies Summary
Transit Mall Case Studies Summary Location Key Features Potential Lessons for Market Street Successful Transit Malls Seattle Third Avenue Four lanes, all transit‐only. Through careful coordination of Right lane is used for stops, left signal timing, aggressive lane for passing. enforcement and optimal stop spacing, San Francisco can Buses grouped into three, each significantly improve bus travel stopping every three blocks. times on Market Street. During peak hours, restricted Consider having all buses and auto access to all lanes, with streetcars stop every other forced right turns about every 2 block. blocks. Because of F‐Line tracks, Aggressive enforcement of consider reversing Seattle’s auto restrictions and cross‐ arrangement, with all buses rd traffic backing up across 3 and streetcars stopping at Avenue at red lights. extended boarding islands in Buses run 26% faster on the left lane, and using the surface street than they did in right lane to allow buses to dedicated bus subway. pass. For wider boarding islands and to bypass cars queued to turn right, consider moving boarding islands midblock. Vancouver Granville Mall Older transit mall, with two For retail and pedestrian transit‐only lanes. success, a high level of investment in materials, To revitalize retail along mall, finishing, storefronts and some community members programming is critical. urged opening the mall to vehicle traffic. City decided to maintain current configuration but refresh materials and finishes. One block to be built without curbs as a pedestrian priority space. Portland Mall Even with Portland’s small Consider auto restrictions only (200’) blocks, the previous at peak hours in order to transit‐only mall was maintain the “urban energy” considered to be a failure for associated with sufficient pedestrians and retail. -

20190204 Tip Sheet 4
PBOT GLOSSARY OCTOBER 2019 cut-through (n. and adj.) FEMA Acronym for the Federal reference to lanes sometimes referred write alone. Otherwise, note ODOT Acronym for the Oregon PPP Internal abbreviation for the Policy, runoff (n.) speed hump NACTO term for what the Transit Mall Capitalize in reference to Style guide for writing common terms, acronyms, and programs for public communications. Emergency Management Agency. Write to as carpool lanes by the public, but capitalization in MAX Light Rail. Department of Transportation. Write out Planning & Projects group. Do not use in Portland public is most likely to see on the Portland Transit Mall whether or not DEI Increasingly common abbreviation out on first usage. which are also used by transit, vanpools, on first usage. public communications. rush hour (n.), rush-hour (adj.) local streets and call speed bumps, often the word Portland appears. for diversity, equity, and inclusion in Lowercase generally when alone. etc. Write out on first usage, note mayor indicated by signage that says “bump.” describing training, courses, and other Capitalize only in formal titles with the predesignated Safe Routes to School PBOT program. FHWA Acronym for the Federal Highway hyphen in high-occupancy. Avoid OMF Abbreviation for city’s Office of Define on first usage and use pictures to TransitTracker Written as one word, This glossary is the work of the PBOT Communications team, with guidance from the 2018 Associated Press Stylebook, consultation with opportunities to engage on these topics. person’s name. Also: mayoral, mayor’s Note capitalization. Do not use Administration. Write out on first usage. -
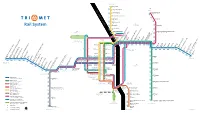
Rail System Map with Bus Transfers
N PORTLAND Expo Center 11 Delta Park/Vanport WILLAMETTE RIVER 6 - AIRPORT Kenton/Denver Portland Airport 4 - N Lombard Transit Center 4 75 14 min 19 min Rosa Parks Mt Hood 44 N Killingsworth 72 NE Rail System N Prescott PORTLAND Cascades Overlook Park NW Albina/Mississippi Parkrose/Sumner Transit Center PORTLAND 35 85 12 21 71 73 - Broadway Northrup Weidler 23rd Interstate Lovejoy 15 19 22 23 24 25 87 UNION Rose Quarter 4 8 44 77 85 - 66 75 77 71 72 77 35 Rose Quarter Convention Transit6 Center CenterNE 7th Lloyd8 70Center/NEHollywood 11th TransitNE 60th Center NE 82nd Gateway/NETransit Center 99th NW Portland to STATION South Waterfront: 32 min 15 min 73 NW Hoyt NW Glisan 7th 25 87 E 102nd15 20 E 122nd E 148th E 162nd74 E 172nd E 181st Rockwood/E 188th 6th 5th Old Town 20 25 11th 10th Ruby Junction/E 197th NW Davis NW Couch Chinatown Convention Center/NE 7th 25 min to OMSI: 13 min Civic Dr 2 21 82 1st Gresham City Hall2 9 20 21 80 81 82 84 x/Hillsboro Airport Skidmore Gresham Central Transit Center SW Pine SW Oak Fountain Cleveland o Galleria Pioneer Oak/SW 1st Morrison SW 10th Square N SW 3rd SE Main Hatfield GovernmentHillsboro 46 Center47 Centra 48 Tuality57 l/SE Hospita 3rd TransitWashingtol/SE Center 8th n/SEFair 12th Comple 46 Hawthorn Farm 15 Orenc 47 GRESHAM a/SW 170th Martin Luther King Jr Martin Luther 17 min Quatama Providence Park 18th Pioneer Courthouse Pioneer Place Willow Creek/SW 185th TransitSW 158th Center 52 59 88 / 15 18 24 51 63 Grand HILLSBORO Elmonic 20 48 50 59 62 SE Division 2 Merlo 63 Yamhill 67 Library