Unbounded Color Engines
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Cielab Color Space
Gernot Hoffmann CIELab Color Space Contents . Introduction 2 2. Formulas 4 3. Primaries and Matrices 0 4. Gamut Restrictions and Tests 5. Inverse Gamma Correction 2 6. CIE L*=50 3 7. NTSC L*=50 4 8. sRGB L*=/0/.../90/99 5 9. AdobeRGB L*=0/.../90 26 0. ProPhotoRGB L*=0/.../90 35 . 3D Views 44 2. Linear and Standard Nonlinear CIELab 47 3. Human Gamut in CIELab 48 4. Low Chromaticity 49 5. sRGB L*=50 with RGB Numbers 50 6. PostScript Kernels 5 7. Mapping CIELab to xyY 56 8. Number of Different Colors 59 9. HLS-Hue for sRGB in CIELab 60 20. References 62 1.1 Introduction CIE XYZ is an absolute color space (not device dependent). Each visible color has non-negative coordinates X,Y,Z. CIE xyY, the horseshoe diagram as shown below, is a perspective projection of XYZ coordinates onto a plane xy. The luminance is missing. CIELab is a nonlinear transformation of XYZ into coordinates L*,a*,b*. The gamut for any RGB color system is a triangle in the CIE xyY chromaticity diagram, here shown for the CIE primaries, the NTSC primaries, the Rec.709 primaries (which are also valid for sRGB and therefore for many PC monitors) and the non-physical working space ProPhotoRGB. The white points are individually defined for the color spaces. The CIELab color space was intended for equal perceptual differences for equal chan- ges in the coordinates L*,a* and b*. Color differences deltaE are defined as Euclidian distances in CIELab. This document shows color charts in CIELab for several RGB color spaces. -

Harlequin RIP OEM Manual
0RIPMate for Windows operating systems Harlequin PLUS Server RIP v9.0 June 2011 AG12325 Rev. 13 Copyright and Trademarks Harlequin PLUS Server RIP June 2011 Part number: HK‚9.0‚ÄìOEM‚ÄìWIN Document issue: 106 Copyright ¬© 2011 Global Graphics Software Ltd. All rights reserved. Certificate of Computer Registration of Computer Software. Registration No. 2006SR05517 No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, elec- tronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of Global Graphics Software Ltd. The information in this publication is provided for information only and is subject to change without notice. Global Graphics Software Ltd and its affiliates assume no responsibility or liability for any loss or damage that may arise from the use of any information in this publication. The software described in this book is furnished under license and may only be used or cop- ied in accordance with the terms of that license. Harlequin is a registered trademark of Global Graphics Software Ltd. The Global Graphics Software logo, the Harlequin at Heart Logo, Cortex, Harlequin RIP, Harlequin ColorPro, EasyTrap, FireWorks, FlatOut, Harlequin Color Management System (HCMS), Harlequin Color Production Solutions (HCPS), Harlequin Color Proofing (HCP), Harlequin Error Diffusion Screening Plugin 1-bit (HEDS1), Harlequin Error Diffusion Screening Plugin 2-bit (HEDS2), Harlequin Full Color System (HFCS), Harlequin ICC Profile Processor (HIPP), Harlequin Standard Color System (HSCS), Harlequin Chain Screening (HCS), Harlequin Display List Technology (HDLT), Harlequin Dispersed Screening (HDS), Harlequin Micro Screening (HMS), Harlequin Precision Screening (HPS), HQcrypt, Harlequin Screening Library (HSL), ProofReady, Scalable Open Architecture (SOAR), SetGold, SetGoldPro, TrapMaster, TrapWorks, TrapPro, TrapProLite, Harlequin RIP Eclipse Release and Harlequin RIP Genesis Release are all trademarks of Global Graphics Software Ltd. -

NEC Multisync® PA311D Wide Gamut Color Critical Display Designed for Photography and Video Production
NEC MultiSync® PA311D Wide gamut color critical display designed for photography and video production 1419058943 High resolution and incredible, predictable color accuracy. The 31” MultiSync PA311D is the ultimate desktop display for applications where precise color is essential. The innovative wide-gamut LED backlight provides 100% coverage of Adobe RGB color space and 98% coverage of DCI-P3, enabling more accurate colors to be displayed on screen. Utilizing a high performance IPS LCD panel and backed by a 4 year warranty with Advanced Exchange, the MultiSync PA311D delivers high quality, accurate images simply and beautifully. Impeccable Image Performance The wide-gamut LED LCD backlight combined with NEC’s exclusive SpectraView Engine deliver precise color in every environment. • True 4K resolution (4096 x 2160) offers a high pixel density • Up to 100% coverage of Adobe RGB color space and 98% coverage of DCI-P3 • 10-bit HDMI and DisplayPort inputs display up to 1.07 billion colors out of a palette of 4.3 trillion colors Ultimate Color Management The sophisticated SpectraView Engine provides extensive, intuitive control over color settings. • MultiProfiler software and on-screen controls provide access to thousands of color gamut, gamma, white point, brightness and contrast combinations • Internal 14-bit 3D lookup tables (LUTs) work with optional SpectraViewII color calibration solution for unparalleled color accuracy A Perfect Fit for Your Workspace A Better Workflow Future-proof connectivity, great ergonomics, and VESA mount Exclusive, -

Evaluating Gamut Coverage Metrics for ICC Color Profiles
International Journal of Chaotic Computing (IJCC), Volume 4, Issue 2, December 2016 Evaluating Gamut Coverage Metrics for ICC Color Profiles Radu Velea1, Noel Gordon2 1Technical Military Academy of Bucharest, Romania 2Google Inc Abstract The color handling characteristics of computer the input media. The objective is to maintain color monitors and other display devices can significantly accuracy across heterogeneous displays. alter the way an image is perceived by the human eye. Modern cameras and software applications can create vibrant color scenes, and can specify the color range (or gamut) of the scene with an embedded ICC profile [1]. During presentation, differences in the color gamut of the image and the display device require color management to help preserve the color Figure 1. ICC v2 color profile transform. fidelity of the image when shown on different displays. Measurements of the color characteristics However, since gamut is a physical device of display devices is thus a topic of interest. This property, if an input color can not be physically paper evaluates the ability of gamut measures, reproduced by the destination gamut, unavoidable including those commonly used in industry, to color distortion results [2], which may be perceived classify display gamuts using a user-contributed by users. It is therefore important to know (a priori, dataset of ICC display color profiles, and if possible) the end-user viewing conditions in which recommends the use of relative metrics for gamut the input media will be displayed. comparison tasks. Motivation- Gamut classification of display 1. Introduction profiles can yield valuable information on the way color is perceived in end-user systems. -

How to Use the Engine in Your Applications 2.12
How to use the engine in your applications 2.12 https://www.littlecms.com Copyright © 2020 Marti Maria Saguer, all rights reserved. Introduction 2 Table of Contents Introduction ........................................................................................................................ 4 Documentation ............................................................................................................... 5 Requeriments ................................................................................................................. 6 Include files .................................................................................................................... 6 Basic Concepts .............................................................................................................. 7 Source code conventions ............................................................................................... 7 The const keyword ......................................................................................................... 7 The register keyword ...................................................................................................... 7 Basic Types.................................................................................................................... 8 Step-by-step Example ........................................................................................................ 9 Open the profiles ......................................................................................................... -

Ecma TC46 Issues List
Ecma TC46 Issues List February 2008 A B C D E F Reference (major) Reference Issue Type Comment Status Change (clause) (Editorial/ Applied Technical/ Other 1 Editorial Throughout Technical Change ―may‖ to ―can‖ or ―might‖, as appropriate. ―may‖ is a particularly problematic term when used in the negative. Of course, if the use of "may" is intended to be Accepted WD1.1 normative, "COULD" or "SHOULD" should be used instead. 2 Editorial Throughout Editorial Various on-going editorial tasks: Add non-breaking spaces, as appropriate, so that certain line breaks look better. Add forward references, as appropriate. 3 Editorial Throughout Editorial Mark all defining entries in the cross-reference index so they appear in bold in the index. 4 Normative References & Throughout Editorial Check all RFCs and other specs referenced in the text to see if they are in the normative references list or bibliography, as appropriate. Accepted WD1.1 Bibliography 5 Normative References & Electronic annexes Editorial Add text mentioning the electronic versions of schemas and their normative status. Accepted WD1.1 Bibliography 6 Editorial Throughout Editorial Consider replacing cross-references of the form ‗see §s, ―xxx,‖ on page pp‘ with ‗see §s‘. Page number references are not really relevant in an electronic document, and it's not Accepted WD1.1 clear that having the clause name as well as number is useful. 7 Normative References & Draft 1.0.1, 9.3 Technical Resolve references to .NET and Windows Presentation Foundation. Bibliography 8 Colour Draft 1.0.1, 15.1.8-Technical Decide what, if anything, to do about private Microsoft ICC and ―MS00‖ signature. -

Specification ICC.1:2004-10 (Profile Version 4.2.0.0)
ICC.1:2004-10 International Color Consortium® Specification ICC.1:2004-10 (Profile version 4.2.0.0) Image technology colour management — Architecture, profile format, and data structure [REVISION of ICC.1:2003-09] With errata incorporated, 5/22/2006 © ICC 2004 – All rights reserved i ICC.1:2004-10 Copyright notice Copyright © 2004 International Color Consortium® Permission is hereby granted, free of charge, to any person obtaining a copy of this Specification (the “Specifi- cation”) to exploit the Specification without restriction including, without limitation, the rights to use, copy, mod- ify, merge, publish, distribute, and/or sublicense, copies of the Specification, and to permit persons to whom the Specification is furnished to do so, subject to the following conditions: Elements of this Specification may be the subject of intellectual property rights of third parties throughout the world including, without limitation, patents, patent application, utility, models, copyrights, trade secrets or other proprietary rights (“Third Party IP Rights”). Although no Third Party IP Rights have been brought to the atten- tion of the International Color Consortium (the “ICC”) by its members, or as a result of the publication of this Specification in certain trade journals, the ICC has not conducted any independent investigation regarding the existence of Third Party IP Rights. The ICC shall not be held responsible for identifying Third Party IP Rights that may be implicated by the practice of this Specification or the permissions granted above, for conducting inquiries into the applicability, existence, validity, or scope of any Third Party IP Rights that are brought to the ICC’s attention, or for obtaining licensing assurances with respect to any Third Party IP Rights. -

Working with Wide Color Gamut in Final Cut Pro X New Workflows for Editing
Working with Wide Color Gamut in Final Cut Pro X New Workflows for Editing White Paper October 2016 Contents Page 3 Introduction Page 4 Background Page 6 Sources of Wide-Gamut Video Page 7 Wide Color Gamut in Final Cut Pro X Setting Up Rec. 2020 in Final Cut Pro Changing a Project’s Color Space Exporting a Wide-Gamut Project About Displays and ColorSync Monitoring a Wide-Gamut Project Page 12 Delivery to Multiple Color Spaces Matching colors in Rec. 2020 and Rec. 709 masters Preparing for Export Page 14 Key Takeaways Page 15 Conclusion Working with Wide Color Gamut in Final Cut Pro X | October 2016 2 Introduction In 2015, Apple began introducing devices that record and display more colors than ever before. Final Cut Pro X 10.3 supports not only these new cameras and displays, but also a new industry standard that delivers more colorful photo and video content across a wide range of professional devices. This white paper discusses the concepts behind these new capabilities, and describes recommended workflows. Working with Wide Color Gamut in Final Cut Pro X | October 2016 3 Background Since the introduction of high-definition television in the 1990s, HDTV displays have been limited to a standard range of colors defined by an industry specification for HDTV broadcasts called Rec. 709 (ITU-R Recommendation BT.709). This range of colors, or color gamut, is a subset of all the colors visible to the human eye. The Rec. 709 color gamut was based on the color characteristics of cathode-ray tube (CRT) displays in use around 1990. -

Colour Vision Deficiency Transforms Using ICC Profiles
©2016 Society for Imaging Science and Technology Colour vision deficiency transforms using ICC profiles Phil Green, Peter Nussbaum, Norwegian Colour & Visual Computing Laboratory, Gjøvik University College, Norway Abstract or Daltonization transform to reflect the degree of deficiency experienced by the anomalous observer. Finally, it may be desired We show how ICC profiles can be used to handle a variety of to apply the matching functions of the CVD observer to spectral data transforms intended to either simulate the appearance of a colour in order to estimate the spectral response of the observer. image to an observer with a colour vision deficiency (CVD), or Both simulation and Daltonization algorithms typically take adjust the image to improve the discriminability of colours to the the form of a conversion from XYZ to LMS, followed by a linear CVD observer. In ICC v4, the different profile classes transform conversion to a modified LMS space that corresponds to the type between a data encoding and the ICC Profile Connection Space and degree of colour deficiency, and finally a transform back to (with the exception of the DeviceLink profile, which is a transform XYZ from modified LMS. In a Daltonization algorithm, a further between two data encodings). Some simulation and Daltonization operation is performed on the modified LMS data to shift those algorithms can be concatenated into a single matrix, which can be spectra that are difficult for the CVD observer to discriminate into encoded as a v4 LUT-based profile or a matrix/curve profile. the visible range, based on the magnitude of the difference between Alternatively a more complex transform can be encoded in the the original and CVD-simulated image. -

Recording Devices, Image Creation Reproduction Devices
11/19/2010 Early Color Management: Closed systems Color Management: ICC Profiles, Color Management Modules and Devices Drum scanner uses three photomultiplier tubes aadnd typica lly scans a film negative . A fixed transformation for the in‐house system Dr. Michael Vrhel maps the recorded RGB values to CMYK separations. Print operator adjusts final ink amounts. RGB CMYK Note: At‐home, camera film to prints and NTSC television. TC 707 Basis of modern techniques for color specification, measurement, control and communication. 11/17/2010 1 2 Reproduction Devices Recording Devices, Image Creation 3 4 1 11/19/2010 Modern Color Modern Color Communication: Communication: Open systems. Open systems. Profile Connection Space (PCS) e.g. CIELAB, CIEXYZ or sRGB 5 6 Modern Color Communication: Open Standards, Standards, Standards.. Systems. Printing Industry: ICC profile as an ISO standard Postscript color management was the first adopted solution providing a connection ISO 15076‐1:2005 Image technology colour management Space 1990 in PostScript Level 2. Architecture, profile format and data structure ‐‐ Part 1: Based on ICC.1:2004‐10 Apple ColorSync was a competing solution introduced in 1993. Camera characterization standards ISO 22028‐1 specifies the image state architecture and encoding requirements. International Color Consortium (ICC) developed a standard that has now been widely ISO 22028‐3 specifies the RIMM, ERIMM (and soon the FP‐RIMM) RGB color encodings. adopted at least by the print industry. Organization founded in 1993 by Adobe, Agfa, IEC/ISO 61966‐2‐2 specifies the scRGB, scYCC, scRGB‐nl and scYCC‐nl color encodings. Kodak, Microsoft, Silicon Graphics, Sun Microsystems and Taligent. -
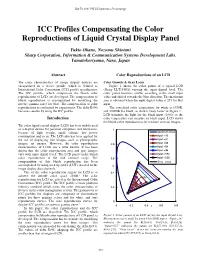
ICC Profiles Compensating the Color Reproductions of Liquid Crystal Display Panel
IS&T©s 2001 PICS Conference Proceedings ICC Profiles Compensating the Color Reproductions of Liquid Crystal Display Panel Yukio Okano, Nozomu Shiotani Sharp Corporation, Information & Communication Systems Development Labs. Yamatokoriyama, Nara, Japan Abstract Color Reproductions of an LCD The color characteristics of image display devices are Color Gamuts & Gray Locus encapsulated in a device profile, which is defined as Figure 1 shows the color gamut of a typical LCD International Color Consortium (ICC) profile specification. (Sharp LLT1510A) varying the input digital level. The The ICC profiles, which compensate the bluish color color gamut becomes smaller according to the small input reproductions of LCD, are developed. The compensation of value and shifted towards the blue direction. The maximum bluish reproduction is accomplished by modifying the area is obtained when the input digital value is 255 for 8bit inverse gamma curve for blue. The compensation of color input. reproductions is confirmed by experiments. The delta E(94) The correlated color temperature for white is 6729K, becomes smaller by using the ICC profile. and 29000K for black, as shown “Gray locus” in Figure 1. LCD transmits the light for the black input (0,0,0) so the Introduction color temperature can measure in black input. LCD shows the bluish color reproductions for medium contrast images. The color liquid crystal display (LCD) has been widely used as a display device for personal computers and televisions, 1 because of light weight, small volume, low power spectrum locus consumption and so on. The LCD also has been applied for Input =16 the use of displaying fine images, such as photographic Input =32 images, art images. -

Color in PDF/A-1
PDF/A Competence Center TechNote 0002: Color in PDF/A-1 The PDF/A-1 requirements related to color handling may be confusing to users and developers who are not familiar with color management concepts and ICC profiles. This TechNote describes the affected objects in PDF, details the require- ments of PDF/A-1 with respect to color handling, and provides recommenda- tions for color strategies in common situations. Contrary to popular belief, specifying an RGB value for, say, black does not accu- rately specify any color, but merely instructs a particular device to render the darkest possible color – which will be different on different devices. Similarly, 50% red in RGB may look like a clearly specified color, but it fails to define the red base color to use. Again, the visual results will be different on multiple out- put devices. These problems can be solved by using device-independent color specifications. Since PDF/A-1 is targeted at long-time preservation of the document’s visual appearance, device-independent color specification methods are required. PDF/A-1 makes use of several PDF concepts for specifying color without any de- pendency on actual output devices. 2008-03-14 page 1 PDF/A Competence Center 1 PDF Color Concepts 1.1 Color Spaces in PDF PDF supports various color spaces which can be grouped as follows: • Device color spaces refer to a specific output technology, and cannot be used to specify color values such that colors are reproducible in a predictable way across a range of output devices: DeviceGray, DeviceRGB, DeviceCMYK.