DOCSLIB.ORG

A Dynamical Interpretation of the Wind Field in Tropical Cyclones with the Consideration of Orographic Factors

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Dynamical Interpretation of the Wind Field in Tropical Cyclones with the Consideration of Orographic Factors Vol.16 No.2 JOURNAL OF TROPICAL METEOROLOGY June 2010 Article ID: 1006-8775(2010) 02-0125-09 A DYNAMICAL INTERPRETATION OF THE WIND FIELD IN TROPICAL CYCLONES WITH THE CONSIDERATION OF OROGRAPHIC FACTORS 1 1 2 3 HAO Shi-feng (郝世峰) , PAN Jin-song (潘劲松) , YUE Cai-jun (岳彩军) , CUI Xiao-peng (崔晓鹏) , YANG 1 Shi-fang (杨诗芳) (1. Zhejiang Meteorology Observatory, Hangzhou 310017 China; 2. Shanghai Typhoon Institute of China Meteorological Administration, Shanghai 200030 China; 3. LACS, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029 China) Abstract: Based on the barotropic primitive equation in the polar coordinate system and the appropriate assumption, we obtained the mathematical equation of orographic forcing on unit mass air parcel. With the consideration of the frictional stress of the sea and land, supposing that parcel velocity in tropical cyclones is in linear variation and that the distribution of surface pressure is circular, a set of equations are derived, which describe the impact of orographic slope error, the central pressure error and position error of tropical cyclones on the wind field in the tropical cyclone. Typhoon Wipha (2007) is selected to verify the above interpretation method. The results show that the orographic slope, the frictional coefficient, the intensity and position of the cyclone are the important factors which have great influence on the interpretation of wind information about tropical cyclones. The dynamic interpretation method gives very good results, especially for the coastal area. It is applicable to improving the forecasts of the wind field in tropical cyclones. Key words: tropical cyclone; orographic slope; frictional stress; strong wind; dynamic interpretation CLC number: P444 Document code: A doi: 10.3969/j.issn.1006-8775.2010.02.004 1 INTRODUCTION cyclones. In order to improve numerical forecasts, a lot of efforts have been made to refine model capability, Tropical cyclones are intense synoptic systems enhance initial fields, etc. However, forecast errors are which occur over the tropical ocean. Since the inevitable since the permanent existence of data errors conventional synoptic observations over the ocean are and model errors. Then how to interpret products of rare and unreliable, it is difficult to know the true numerical forecasts and lessen the influence of the structure of tropical cyclones and associated above mentioned errors becomes an important task. characteristics. Although there exist plenty of satellite Presently, methods for interpretation of products of observations, it is still difficult to get very good results numerical forecasts mainly include statistical due to some reasons, such as difficulties in assimilation interpretation (such as MOS, PP and Kalman filter), technology. They are the most important reasons that synoptic interpretation, artificial intelligence lead to the difficulties of forecasts of tracks, intensities, interpretation, etc. While no matter which method to wind and rainfall associated with tropical cyclones. select, the key factors influencing the errors must be The disasters caused by tropical cyclones are taken into account. According to the particularity of mainly induced by strong wind and heavy rainfall. typhoons’ structure, some reasonable typhoon models Torrential rainfall, especially typhoon-induced are set up by incorporating the main factors which torrential rainfall, has been studied extensively by [1-5] influence the wind and pressure field of tropical many scholars at home and abroad , but few studies cyclones, such as the Fujita formula, Myers formula have been carried out on the strong wind of tropical and a tangential wind velocity profile scheme by Received date: 2009-12-11; revised date: 2010-03-02 Foundation item: National Basic Research Program of China (973 Program) (2009CB421505); major projects for science and technology development of Zhejiang province (2007C13G1610002); major promoting projects for new technology of China Meteorologycal Administration (09A13) Biography: HAO Shi-feng, senior engineer, M.S., mainly undertaking the research on numerical predication. E-mail for corresponding author: [email protected] PDF created with pdfFactory trial version www.pdffactory.com 126 Journal of Tropical Meteorology Vol.16 Williams in 1987, and applied to practical operations. 2 [6] [7] ìdvr vq ¶f Zou and Xiao and Pu and Braun constructed ï-fvFq-=-+r Bogus schemes by using typhoon models and ïdtrr¶ assimilated them into initial fields, which improved ïdvvv 1 ¶f qq+r+fvF=-+, (1) forecasts. These simplified typhoon models could í r q ï dtrr¶q describe the main characteristics of typhoons since they ï¶f ® have the key factors. While the wind fields of these ï+Ñ·(f -=ghv)0 typhoon models are mainly symmetric, which are î¶t different from those of actual typhoons with apparent in which Fr and Fq are the frictional stress, h is asymmetric features, Lei and Chen [8] showed that the the height of terrain, and all other notations here are distributions of the physical fields associated with conventional in the meteorological context. The typhoons are often asymmetric due to the influences of subscripts “q ” and “ r ” indicate the tangential and the moving speed, frictional stress and environmental radial directions, respectively. Supposing that the synoptic systems. Many researches have focused on the geopotential equation of Eq.(1) is for stationary motion, asymmetric structures of typhoons at home and abroad. [9] ¶f Zhang and Sui put forward a model of wind fields of = 0 , and the distribution of geopotential height in typhoons by considering frictions in stable state in ¶t 1989, and discussed it under ideal conditions. Hu et al. tropical cyclones is circular, namely the zero order [10] and Huang et al. [11] further studied the model, ¶f approximation[13, 14], = 0 , the geopotential verified it by using wind fields of real typhoon cases r¶q and pointed out that this model was applicable in equation can be expressed as: describing the asymmetric distribution of wind fields of ¶f ®® tropical cyclones. vr =v·Ñgh-()f -Ñhgv. (2) In the previous work, researches are mainly ¶r restricted to the wind field of tropical cyclones on the By introducing the equation of continuity, Eq.(2) sea level. Hao et al[12] studied the dynamical can be further written as interpretation of wind field of tropical cyclones over ¶f ® v=v·Ñ+ghgw (3) the sea. Due to not considering the orographical factors, rs¶r their researches show that the interpretation effect is where w is the vertical velocity over the surface, not good on land, and the wind field on islands was not s which is the sum of vertical velocity caused by improved after the tropical cyclone landfalling. In this [15] paper, a dynamical interpretation method of wind fields orographic uplift and frictional effect , C ® of tropical cyclones, in which orographical factors wx=d +vh·Ñ , where x is the vorticity over were considered, is proposed by combining the method s f proposed by Hao with operational forecasts and by the surface, and C is the drag coefficient. By analyzing the key factors influencing wind fields in d tropical cyclones. substituting ws into Eq.(3) we obtain ¶f gCg¶¶hh =d x ++2()vv v ¹ 0 . (4) 2 DYNAMICAL INTERPRETATION ¶rvfvq rr¶¶q r r METHOD OF WIND FIELDS IN TROPICAL rr CYCLONES In Eq.(4), the second term expresses the radial orographic forcing on unit mass air parcel in tropical 2.1 Correction equation of numerical forecasts of cyclones on the condition that the atmosphere is wind fields in tropical cyclones barotropic, which is associated with the orographic slope, wind speed, and the angle between the wind By setting the center of tropical cyclones as the direction and orographic slope. Set the second term of origin of polar coordinates, the barotropical primitive Eq.(4) as equations of any air parcel in tropical cyclones could g¶¶hh be expressed as: frr=+2()vvq . (5) vrrr¶¶q Because the direction of forcing caused by the orographic slope and the orographic gradient are collinear, the tangential forcing caused by the orographic slope is PDF crea126t ed with pdfFactory trial version www.pdffactory.com No.2 HAO Shi-feng (郝世峰), PAN Jin-song (潘劲松) et al. 127 g¶h¶¶hh suitable to study the wind field over land surface f=+2[vv()21()]- . (6) qqvr¶qq¶¶rrr directly, they were introduced into the primitive r equation as modified terms as follows: As Eqs. (5 & 6) were obtained on the condition that the atmosphere is barotropic, which are not 2 ìdvrvq12¶pg¶¶hh ï-fvqq-=--d ()v++vFrr ïdtrrq¶rvrr¶¶ í r (7) dvvv 12¶pg¶h¶¶hh ïqq+r+fv=--d[v()21()]-++vF ï rrqq îdtrr¶qvrr¶qq¶¶rr 1 ¶p tropical cyclones is circular, -=0 , considering where d is the modified coefficient. r ¶q Supposing that parcel velocity takes on linear the influence of the speed of movement of tropical variation in tropical cyclones, that is, [16] cyclones, vs , on the cyclonic curvature radius r , dvr dvq = Cr , =-Cq are constants, further and setting the counter-clockwise direction to be dt dt positive, the frictional stress to be proportional to the supposing that the distribution of sea level pressure in square of wind speed and k to be frictional coefficient. Eq.(7) could be further written as: 2 ìvqqvvscosa 12¶pg¶¶hh 22 ï ++fvq=+d ()vqq+vr+kvrv++vCrr ïrrrq¶rvrr¶¶ í r (8) vvvv cosa2g¶h¶¶hh ïrq+rs +fv=-d[v()2()]-1+v-kvv22++vC ï rqrrqqq îrrvrr¶qq¶¶rr where a is the angle between the moving direction of ¶h Ng= 2d , and Q=+vv22, Eq.(8) can be tropical cyclones and the tangential direction of parcels. ¶r q r 1 ¶p ¶h By setting p = , Mg= 2d , expressed alternatively as: r ¶r r¶q 2 ìvqqvvscosa 1 ï++fvqq=p +()vM+vrN++kvrrQC ïrrv í r . (9) vvvv cosa 1 ïqr+rs +fv=-()vM21N- +vM-+kvQC ï rrqqq îrrvr Since the orographic slope is constant, obtain the influence of the error of the orographic slope ¶NM on wind speed as follows: MN22+=const , we can obtain =- .
Load more

Recommended publications
  • Secessionist Activity Behind Solo Travel
    CHINA DAILY | HONG KONG EDITION Friday, August 2, 2019 | 3 TOP NEWS 7th Military Secessionist Games torch rally lauds activity behind PLA birth By ZHAO LEI solo travel ban [email protected] A torch relay for the upcoming 7th International Military Sports Individual permits to visit Taiwan Council Military World Games first allowed on trial basis in June 2011 began on Thursday in Nanchang, Jiangxi province. The flame was lit at a ceremony on By ZHANG YI “The launch of individual travel Thursday morning in front of a [email protected] permits in 2011 was a positive meas­ sculpture of Communist Party of ure to expand exchanges across the China revolutionaries inside the Ma Xiaoguang, spokesman for Straits in the climate of the peaceful The bed of Hongze Lake is exposed as water recedes due to the worst drought in decades in Nanchang August 1st Memorial Hall. the State Council’s Taiwan Affairs development of cross­Straits rela­ Huai’an, Jiangsu province, on Wednesday. PROVIDED TO CHINA DAILY Fang Minglu, the great­grand­ Office, said on Thursday that it is the tions,” Ma said. daughter of Fang Zhimin, a revolu­ island’s ruling Democratic Progres­ For years, mainland residents tionary martyr, lit the torch with a sive Party’s “Taiwan independence” visiting Taiwan played a positive concave mirror using the sun’s rays. secessionist activities that led to the role in promoting the development Business dries up for fishermen, Later, she passed the flame to a PLA suspension of individual travel per­ of Taiwan's tourism and related soldier who transferred it to a carrier.
    [Show full text]
  • Sigma 1/2008
    sigma No 1/2008 Natural catastrophes and man-made disasters in 2007: high losses in Europe 3 Summary 5 Overview of catastrophes in 2007 9 Increasing flood losses 16 Indices for the transfer of insurance risks 20 Tables for reporting year 2007 40 Tables on the major losses 1970–2007 42 Terms and selection criteria Published by: Swiss Reinsurance Company Economic Research & Consulting P.O. Box 8022 Zurich Switzerland Telephone +41 43 285 2551 Fax +41 43 285 4749 E-mail: [email protected] New York Office: 55 East 52nd Street 40th Floor New York, NY 10055 Telephone +1 212 317 5135 Fax +1 212 317 5455 The editorial deadline for this study was 22 January 2008. Hong Kong Office: 18 Harbour Road, Wanchai sigma is available in German (original lan- Central Plaza, 61st Floor guage), English, French, Italian, Spanish, Hong Kong, SAR Chinese and Japanese. Telephone +852 2582 5691 sigma is available on Swiss Re’s website: Fax +852 2511 6603 www.swissre.com/sigma Authors: The internet version may contain slightly Rudolf Enz updated information. Telephone +41 43 285 2239 Translations: Kurt Karl (Chapter on indices) CLS Communication Telephone +41 212 317 5564 Graphic design and production: Jens Mehlhorn (Chapter on floods) Swiss Re Logistics/Media Production Telephone +41 43 285 4304 © 2008 Susanna Schwarz Swiss Reinsurance Company Telephone +41 43 285 5406 All rights reserved. sigma co-editor: The entire content of this sigma edition is Brian Rogers subject to copyright with all rights reserved. Telephone +41 43 285 2733 The information may be used for private or internal purposes, provided that any Managing editor: copyright or other proprietary notices are Thomas Hess, Head of Economic Research not removed.
    [Show full text]
  • October 2013 Global Catastrophe Recap 2 2
    October 2013 Global Catastrophe Recap Table of Contents Executive0B Summary 3 United2B States 4 Remainder of North America (Canada, Mexico, Caribbean, Bermuda) 4 South4B America 4 Europe 4 6BAfrica 5 Asia 5 Oceania8B (Australia, New Zealand and the South Pacific Islands) 6 8BAAppendix 7 Contact Information 14 Impact Forecasting | October 2013 Global Catastrophe Recap 2 2 Executive0B Summary . Windstorm Christian affects western and northern Europe; insured losses expected to top USD1.35 billion . Cyclone Phailin and Typhoon Fitow highlight busy month of tropical cyclone activity in Asia . Deadly bushfires destroy hundreds of homes in Australia’s New South Wales Windstorm Christian moved across western and northern Europe, bringing hurricane-force wind gusts and torrential rains to several countries. At least 18 people were killed and dozens more were injured. The heaviest damage was sustained in the United Kingdom, France, Belgium, the Netherlands and Scandinavia, where a peak wind gust of 195 kph (120 mph) was recorded in Denmark. More than 1.2 million power outages were recorded and travel was severely disrupted throughout the continent. Reports from European insurers suggest that payouts are likely to breach EUR1.0 billion (USD1.35 billion). Total economic losses will be even higher. Christian becomes the costliest European windstorm since WS Xynthia in 2010. Cyclone Phailin became the strongest system to make landfall in India since 1999, coming ashore in the eastern state of Odisha. At least 46 people were killed. Tremendous rains, an estimated 3.5-meter (11.0-foot) storm surge, and powerful winds led to catastrophic damage to more than 430,000 homes and 668,000 hectares (1.65 million) acres of cropland.
    [Show full text]
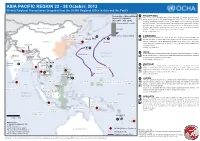
  • Pdf | 431.12 Kb
    ASIA PACIFIC REGION 22 - 28 October, 2013 Weekly Regional Humanitarian Snapshot from the OCHA Regional Office in Asia and the Pacific 1 PHILIPPINES Probability of Above/Below As of 21 Oct, the 7.2M earthquake in Bohol had killed 186 people, affected some 3 Normal Precipitation r" million, and left nearly 381,000 people displaced of whom 70% or 271,000 were staying (Nov 2013 - Jan 2014) outside of established evacuation centers. These people were in urgent need of shelter Above normal rainfall and WASH support. Psycho-social support was identified as an urgent need for children traumatized by the earthquake, which has produced well over 2,000 aftershocks so far. Recently repaired bridges and roads have opened greater access to affected locations M O N G O L I A normal in Bohol. The Government has welcomed international assistance. Source: OCHA Sitrep No. 4 DPR KOREA Below normal rainfall 2 CAMBODIA 5 Floods across Cambodia have claimed 168 lives, displaced almost 145,000 and 5 RO KOREA JAPAN r" p" u" affected more than 1.7 million. Waters have begun to recede across the country with the worst affected provinces being Battambang and Banteay Meanchey, where many parts C H I N A LEKIMA KOBE remain flooded. Communities are in urgent need of clean water, basic sanitation and BHUTAN emergency shelter. NEPAL p" 5 Source: HRF Sitrep No. 4 KATHMANDU 3 INDIA PA C I F I C Heavy rainfall has been affecting the states of Andhra Pradesh and Odisha, SE India, in BANGLADESH FRANCISCO I N D I A u" the last few days.
    [Show full text]
  • Downloaded 10/05/21 02:09 PM UTC 1426 WEATHER and FORECASTING VOLUME 29
    DECEMBER 2014 W E I 1425 Surface Wind Nowcasting in the Penghu Islands Based on Classified Typhoon Tracks and the Effects of the Central Mountain Range of Taiwan CHIH-CHIANG WEI Department of Digital Content Designs and Management, Toko University, Pu-Tzu City, Chia-Yi County, Taiwan (Manuscript received 5 March 2014, in final form 21 September 2014) ABSTRACT The purposes of this study were to forecast the hourly typhoon wind velocity over the Penghu Islands, and to discuss the effects of the terrain of the Central Mountain Range (CMR) of Taiwan over the Penghu Islands based on typhoon tracks. On average, a destructive typhoon hits the Penghu Islands every 15–20 yr. As a typhoon approaches the Penghu Islands, its track and intensity are influenced by the CMR topography. Therefore, CMR complicates the wind forecast of the Penghu Islands. Six main typhoon tracks (classes I–VI) are classified based on typhoon directions, as follows: (I) the direction of direct westward movement across the CMR of Taiwan, (II) the direction of northward movement along the eastern coast of Taiwan, (III) the direction of northward movement traveling through Taiwan Strait, (IV) the direction of westward movement traveling through Luzon Strait, (V) the direction of westward movement traveling through the southern East China Sea (near northern Taiwan), and (VI) the irregular track direction. The adaptive network-based fuzzy inference system (ANFIS) and multilayer perceptron neural network (MLPNN) were used as the forecasting technique for predicting the wind velocity. A total of 49 typhoons from 2000 to 2012 were analyzed. Results showed that the ANFIS models provided high-reliability predictions for wind velocity, and the ANFIS achieved more favorable performance than did the MLPNN.
    [Show full text]
  • Global 7-Km Mesh Nonhydrostatic Model Intercomparison
    Geosci. Model Dev. Discuss., doi:10.5194/gmd-2016-184, 2016 Manuscript under review for journal Geosci. Model Dev. Published: 2 August 2016 c Author(s) 2016. CC-BY 3.0 License. Global 7-km mesh nonhydrostatic Model Intercomparison Project for improving TYphoon forecast (TYMIP-G7): Experimental design and preliminary results Masuo Nakano1, Akiyoshi Wada2, Masahiro Sawada2, Hiromasa Yoshimura2, Ryo Onishi1, Shintaro 5 Kawahara1, Wataru Sasaki1, Tomoe Nasuno1, Munehiko Yamaguchi2, Takeshi Iriguchi2, Masato Sugi2, and Yoshiaki Takeuchi2 1Japan Agency for Marine-Earth Science and Technology, 3173-25 Showa-machi, Kanazawa-ku, Yokohama, Kanagawa 236-0001, Japan 2Meteorological Research Institute, Japan Meteorological Agency, 1-1 Nagamine, Tsukuba, Ibaraki 305-0052, Japan 10 Correspondence to: Masuo Nakano ([email protected]) Abstract. Recent advances in high-performance computers facilitate operational numerical weather prediction by global hydrostatic atmospheric models with horizontal resolution ~10 km. Given further advances in such computers and the fact that the hydrostatic balance approximation becomes invalid for spatial scales < 10 km, development of global nonhydrostatic models with high accuracy is urgently needed. 15 The Global 7-km mesh nonhydrostatic Model Intercomparison Project for improving TYphoon forecast (TYMIP-G7) is designed to understand and statistically quantify the advantage of high-resolution nonhydrostatic global atmospheric models for improvement of tropical cyclone (TC) prediction. The 137 sets of 5-day simulations using three next-generation nonhydrostatic global models with horizontal resolution 7 km, and conventional hydrostatic global model with horizontal resolution 20 km are run on the Earth Simulator. The three 7-km mesh nonhydrostatic models are the nonhydrostatic global 20 spectral atmospheric Model using Double Fourier Series (DFSM), Multi-Scale Simulator for the Geoenvironment (MSSG), and Nonhydrostatic ICosahedral Atmospheric Model (NICAM).
    [Show full text]
  • Environmental Change and Its Impacts on National Security Changement Environnemental Et Ses Impacts Sur La Sécurité Nationale
    Environmental Change and its impacts on National Security Changement environnemental et ses impacts sur la sécurité nationale Cleo Paskal Associate Fellow, Chatham House, UK Laureate Trudeau Fellow, Centre d'études et de recherches internationales de l'Université de Montréal (CÉRIUM) Centre for National Security Studies, Toronto, 12 February 2018 Geography makes history / La géographie fait l'histoire Edinburgh Castle, Scotland Meherangarh Fort, India Halifax Citadel, Canada Rakvere Catle, Estonia Chatham House | The Royal Institute of International Affairs 2 River trade / Commerce fluvial Chatham House | The Royal Institute of International Affairs 3 Montréal 1851 (avec/with Fort Sainte-Helene 1820s ) Chatham House | The Royal Institute of International Affairs 4 Montréal 2018 Chatham House | The Royal Institute of International Affairs 5 Hong Kong & La Guardia airports/aéroports Chatham House | The Royal Institute of International Affairs 6 Port or airport? Port ou aéroport? Nepal, 2017 La Guardia, Sandy, 2012 Australia, 2017 Aberdeen, 2015 Acapulco, 2013 Delhi, 2013 Dallas-Fort Worth, 2015 Bangkok, 2011 Queensland, 2012 Chatham House | The Royal Institute of International Affairs 7 Rapport du ministère de la Défense sur les risques liés au climat pour l’infrastructure DoD Chatham House | The Royal Institute 8 of International Affairs Rapport: La moitié des sites militaires américains sont vulnérables au changement climatique Homested AFB, 1992 Keesler AFB, 2005 Millington, Tenn, 2010 Chatham House | The Royal Institute 9 of International
    [Show full text]
  • 7.2 AWG Membersreportssummary 2019.Pdf
    ESCAP/WMO Typhoon Committee FOR PARTICIPANTS ONLY 2nd Video Conference INF/TC.52/3.2 Fifty-Second Session 05 June 2020 10 June 2020 ENGLISH ONLY Guangzhou, China SUMMARY OF MEMBERS’ REPORTS 2019 (submitted by AWG Chair) Summary and Purpose of Document: This document presents an overall view of the progress and issues in meteorology, hydrology and DRR aspects among TC Members with respect to tropical cyclones and related hazards in 2019 Action Proposed The Committee is invited to: (a) take note of the major progress and issues in meteorology, hydrology and DRR activities in support of the 21 Priorities detailed in the Typhoon Committee Strategic Plan 2017-2021; and (b) Review the Summary of Members’ Reports 2019 in APPENDIX B with the aim of adopting a “Executive Summary” for distribution to Members’ governments and other collaborating or potential sponsoring agencies for information and reference. APPENDICES: 1) Appendix A – DRAFT TEXT FOR INCLUSION IN THE SESSION REPORT 2) Appendix B – SUMMARY OF MEMBERS’ REPORTS 2019 APPENDIX A: DRAFT TEXT FOR INCLUSION IN THE SESSION REPORT 3.2 SUMMARY OF MEMBERS’ REPORTS 1. The Committee took note of the Summary of Members’ Reports 2019 highlighting the key tropical cyclone impacts on Members in 2019 and the major activities undertaken by Members under the TC Priorities and components during the year. 2. The Committee expressed its sincere appreciation to AWG Chair for preparing the Summary of Members’ Reports and the observations made with respect to the progress of Members’ activities in support of the 21 Priorities identified in the TC Strategic Plan 2017-2021.
    [Show full text]
  • MWL Aug 2014 Draft 1A BOX
    MarinersMariners WEATHER LOGWEATHER LOG Volume 58, Number 2 August 2014 From the Editor Greetings! Welcome to another edition of the Mariners Weather Log. We are smack dab in the middle of hurricane season and our first named storm of the season, Arthur, occurred on July 1st. Tropical Storm Arthur reached hurricane strength on July 3rd off the coast of Mariners Weather Log South Carolina making for a very soggy 4th of July Independence ISSN 0025-3367 Day celebration. Hurricane Arthur has become the first hurricane to make landfall in the continental U.S. since hurricane Isaac struck U.S. Department of Commerce Louisiana on August 28/29th in 2012. With this, I want to remind you Dr. Kathryn D. Sullivan that your marine weather observations really do matter. The data we Under Secretary of Commerce for Oceans and Atmosphere & Acting NOAA Administrator receive from you gets ingested directly into the models, thus you give Acting Administrator the National Weather Service a much better confidence in forecasts National Weather Service and analysis…thank you in advance and we count on your participa- Dr. Louis Uccellini tion. For a full complement of hurricane information you can always NOAA Assistant Administrator for Weather Services go to the National Hurricane Center. For a full explanation on how Editorial Supervisor the Climate Prediction Center in collaboration with the hurricane Paula M. Rychtar experts from the National Hurricane Center and the Hurricane Research Division produce their seasonal outlook you can go to: Layout and Design Stuart Hayes http://www.cpc.ncep.noaa.gov/products/outlooks/hurricane.shtml.
    [Show full text]
  • MEMBER REPORT Japan
    MEMBER REPORT ESCAP/WMO Typhoon Committee 8th Integrated Workshop/2nd TRCG Forum Japan Macao, China 2 ‐ 6 December 2013 CONTENTS I. Overview of tropical cyclones which have affected/impacted Member’s area since the last Typhoon Committee Session II. Summary of progress in Key Result Areas 2 I. Overview of tropical cyclones which have affected/impacted Member’s area in 2013 (Free format) 1. Meteorological Assessment (highlighting forecasting issues/impacts) In 2013, 14 tropical cyclones (TCs) of tropical storm (TS) intensity or higher had come within 300 km of the Japanese islands as of the end of October. Japan was affected by 13 of these, with 2 making landfall. These 13 TCs are described below, and their tracks are shown in Figure 1. (1) TS Leepi (1304) Leepi was upgraded to TS intensity east of the Philippines at 00 UTC on 18 June. Moving northward, it reached its peak intensity with maximum sustained winds of 40 kt and a central pressure of 994 hPa 18 hours later. Leepi passed near Miyakojima Island the next day and transformed into an extratropical cyclone over the East China Sea at 00 UTC on 21 June, and a 24‐hour precipitation total of 222.0 mm was recorded at Ishigakijima (47918). Damage to houses and cancellations of flights and ship departures were reported in Okinawa Prefecture. (2) TY Soulik (1307) Soulik was upgraded to TS intensity around the Mariana Islands at 00 UTC on 8 July, and was further upgraded to TY intensity west of the islands at 00 UTC the next day. Turning west‐northwestward, it developed rapidly and reached its peak intensity with maximum sustained winds of 100 kt and a central pressure of 925 hPa north of Okinotorishima Island at 00 UTC on 10 July.
    [Show full text]
  • The Impact of Typhoon Danas (2013) on the Torrential Rainfall Associated with Typhoon Fitow (2013) in East China
    Hindawi Publishing Corporation Advances in Meteorology Volume 2015, Article ID 383712, 11 pages http://dx.doi.org/10.1155/2015/383712 Research Article The Impact of Typhoon Danas (2013) on the Torrential Rainfall Associated with Typhoon Fitow (2013) in East China Hongxiong Xu1 and Bo Du2 1 State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081, China 2ChinaMeteorologicalAdministrationMeteorologicalObservationCenter,Beijing100081,China Correspondence should be addressed to Hongxiong Xu; [email protected] Received 30 September 2014; Revised 20 January 2015; Accepted 20 January 2015 Academic Editor: Hann-Ming H. Juang Copyright © 2015 H. Xu and B. Du. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. When typhoon Danas (2013) was located at northeast of Taiwan during 6–8 October 2013, a torrential rainfall brought by typhoon Fitow (2013) occurred over the east of China. Observations show that the rainband of Fitow, which may be impacted by Danas, caused the rainfall over north of Zhejiang. The Advanced Research version of the Weather Research and Forecast (ARW-WRF) model was used to investigate the possible effects of typhoon Danas (2013) on this rainfall event. Results show that the model captured reasonably well the spatial distribution and evolution of the rainband of Fitow. The results of a sensitivity experiment removing Danas vortex, which is conducted to determine its impact on the extreme rainfall, show that extra moist associated with Danas plays an important role in the maintenance and enhancement of the north rainband of Fitow, which resulted in torrential rainfall over the north of Zhejiang.
    [Show full text]
  • Report for Typhoon
    Country Report ( 2007 ) For the 40th Session of the Typhoon Committee ESCAP/WMO Macao, China 21–26 November 2007 People’s Republic of China 1 I. Overview of Meteorological and Hydrological Conditions 1. Meteorological Assessment From Oct. 1st 2006 to Sep. 30th 2007, altogether 23 tropical cyclones (including tropical storms, severe tropical storms, typhoons, severe typhoons and super typhoons) formed over the Western North Pacific and the South China Sea (Fig. 1.1). Among them, 8 TCs formed from Oct. 1st to Dec. 31st in 2006 and 4 of them affected China’s coastal waters but didn’t land on China’s coastal areas. They were super typhoon Cimaron (0619), super typhoon Chebi 0620), super typhoon Durian (0621) and severe typhoon Utor (0622). In 2007, 15 tropical cyclones formed over the Western North Pacific and the South China Sea. The number was obviously less than the average (19.7) during the corresponding period from 1949 to 2006. And 9 of them developed into typhoons or beyond, which accounted for 60.0% of the total. The percentage was higher than the average (58.6%). During the same period, 4 TCs formed over the South China Sea. The number was slightly less than the average (4.7). Moreover, 6 TCs made landfalls over China coastal areas, all of them exceed tropical storm category. They were tropical storm Toraji (0703), severe tropical storm Pabuk 0706), tropical storm Wupit 0707), super typhoon Sepat (0708), super typhoon Wipha 0712) and tropical storm Francisco (0713). The total landed TC number was slightly less than the average (about 6.79), but the percentage of landed TCs (40.0%) was obviously above the average (30.8%).
    [Show full text]