An Algorithm for Tracking Eyes of Tropical Cyclones
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Dependence of Probabilistic Quantitative Precipitation Forecast Performance on Typhoon Characteristics and Forecast Track Error in Taiwan
APRIL 2020 T E N G E T A L . 585 Dependence of Probabilistic Quantitative Precipitation Forecast Performance on Typhoon Characteristics and Forecast Track Error in Taiwan HSU-FENG TENG AND JAMES M. DONE National Center for Atmospheric Research, Boulder, Colorado CHENG-SHANG LEE Department of Atmospheric Sciences, National Taiwan University, Taipei, Taiwan YING-HWA KUO National Center for Atmospheric Research, and University Corporation for Atmospheric Research, Boulder, Colorado (Manuscript received 15 August 2019, in final form 7 January 2020) ABSTRACT This study investigates the probabilistic quantitative precipitation forecast (PQPF) performance of ty- phoons that affected Taiwan during 2011–16. In this period, a total of 19 typhoons with a land warning issued by the Central Weather Bureau (CWB) are analyzed. The PQPF is calculated using the ensemble precipi- tation forecast data from the Taiwan Cooperative Precipitation Ensemble Forecast Experiment (TAPEX), and the verification data, verification thresholds, and typhoon characteristics are obtained from the CWB. The overall PQPF performance of TAPEX has an acceptable reliability and discrimination ability, and the higher probability error is distributed at the mountainous area of Taiwan. The PQPF performance is significantly influenced by typhoon characteristics (e.g., typhoon tracks, sizes, and forward speeds). The PQPFs for westward-moving, large, or slow typhoons have higher reliability and discrimination ability, and lower- probability error than those for northward-moving, small, or fast typhoons, except for similar reliability between fast and slow typhoons. Because northward-moving or small typhoons have larger forecast track error, and their PQPF performance is sensitive to the accuracy of the forecast track, a higher probability error occurs than that for westward-moving or large typhoons. -

Secessionist Activity Behind Solo Travel
CHINA DAILY | HONG KONG EDITION Friday, August 2, 2019 | 3 TOP NEWS 7th Military Secessionist Games torch rally lauds activity behind PLA birth By ZHAO LEI solo travel ban [email protected] A torch relay for the upcoming 7th International Military Sports Individual permits to visit Taiwan Council Military World Games first allowed on trial basis in June 2011 began on Thursday in Nanchang, Jiangxi province. The flame was lit at a ceremony on By ZHANG YI “The launch of individual travel Thursday morning in front of a [email protected] permits in 2011 was a positive meas sculpture of Communist Party of ure to expand exchanges across the China revolutionaries inside the Ma Xiaoguang, spokesman for Straits in the climate of the peaceful The bed of Hongze Lake is exposed as water recedes due to the worst drought in decades in Nanchang August 1st Memorial Hall. the State Council’s Taiwan Affairs development of crossStraits rela Huai’an, Jiangsu province, on Wednesday. PROVIDED TO CHINA DAILY Fang Minglu, the greatgrand Office, said on Thursday that it is the tions,” Ma said. daughter of Fang Zhimin, a revolu island’s ruling Democratic Progres For years, mainland residents tionary martyr, lit the torch with a sive Party’s “Taiwan independence” visiting Taiwan played a positive concave mirror using the sun’s rays. secessionist activities that led to the role in promoting the development Business dries up for fishermen, Later, she passed the flame to a PLA suspension of individual travel per of Taiwan's tourism and related soldier who transferred it to a carrier. -

Understanding Disaster Risk ~ Lessons from 2009 Typhoon Morakot, Southern Taiwan
Understanding disaster risk ~ Lessons from 2009 Typhoon Morakot, Southern Taiwan Wen–Chi Lai, Chjeng-Lun Shieh Disaster Prevention Research Center, National Cheng-Kung University 1. Introduction 08/10 Rainfall 08/07 Rainfall started & stopped gradually typhoon speed decrease rapidly 08/06 Typhoon Warning for Inland 08/03 Typhoon 08/05 Typhoon Morakot warning for formed territorial sea 08/08 00:00 Heavy rainfall started 08/08 12:00 ~24:00 Rainfall center moved to south Taiwan, which triggered serious geo-hazards and floodings Data from “http://weather.unisys.com/” 1. Introduction There 4 days before the typhoon landing and forecasting as weakly one for norther Taiwan. Emergency headquarters all located in Taipei and few raining around the landing area. The induced strong rainfalls after typhoon leaving around southern Taiwan until Aug. 10. The damages out of experiences crush the operation system, made serious impacts. Path of the center of Typhoon Morakot 1. Introduction Largest precipitation was 2,884 mm Long duration (91 hours) Hard to collect the information High intensity (123 mm/hour) Large depth (3,000 mm-91 hour) Broad extent (1/4 of Taiwan) The scale and type of the disaster increasing with the frequent appearance of extreme weather Large-scale landslide and compound disaster become a new challenge • Area:202 ha Depth:84 meter Volume: 24 million m3 2.1 Root Cause and disaster risk drivers 3000 Landslide Landslide (Shallow, Soil) (Deep, Bedrock) Landslide dam break Flood Debris flow Landslide dam form Alisan Station ) 2000 -

Sigma 1/2008
sigma No 1/2008 Natural catastrophes and man-made disasters in 2007: high losses in Europe 3 Summary 5 Overview of catastrophes in 2007 9 Increasing flood losses 16 Indices for the transfer of insurance risks 20 Tables for reporting year 2007 40 Tables on the major losses 1970–2007 42 Terms and selection criteria Published by: Swiss Reinsurance Company Economic Research & Consulting P.O. Box 8022 Zurich Switzerland Telephone +41 43 285 2551 Fax +41 43 285 4749 E-mail: [email protected] New York Office: 55 East 52nd Street 40th Floor New York, NY 10055 Telephone +1 212 317 5135 Fax +1 212 317 5455 The editorial deadline for this study was 22 January 2008. Hong Kong Office: 18 Harbour Road, Wanchai sigma is available in German (original lan- Central Plaza, 61st Floor guage), English, French, Italian, Spanish, Hong Kong, SAR Chinese and Japanese. Telephone +852 2582 5691 sigma is available on Swiss Re’s website: Fax +852 2511 6603 www.swissre.com/sigma Authors: The internet version may contain slightly Rudolf Enz updated information. Telephone +41 43 285 2239 Translations: Kurt Karl (Chapter on indices) CLS Communication Telephone +41 212 317 5564 Graphic design and production: Jens Mehlhorn (Chapter on floods) Swiss Re Logistics/Media Production Telephone +41 43 285 4304 © 2008 Susanna Schwarz Swiss Reinsurance Company Telephone +41 43 285 5406 All rights reserved. sigma co-editor: The entire content of this sigma edition is Brian Rogers subject to copyright with all rights reserved. Telephone +41 43 285 2733 The information may be used for private or internal purposes, provided that any Managing editor: copyright or other proprietary notices are Thomas Hess, Head of Economic Research not removed. -

October 2013 Global Catastrophe Recap 2 2
October 2013 Global Catastrophe Recap Table of Contents Executive0B Summary 3 United2B States 4 Remainder of North America (Canada, Mexico, Caribbean, Bermuda) 4 South4B America 4 Europe 4 6BAfrica 5 Asia 5 Oceania8B (Australia, New Zealand and the South Pacific Islands) 6 8BAAppendix 7 Contact Information 14 Impact Forecasting | October 2013 Global Catastrophe Recap 2 2 Executive0B Summary . Windstorm Christian affects western and northern Europe; insured losses expected to top USD1.35 billion . Cyclone Phailin and Typhoon Fitow highlight busy month of tropical cyclone activity in Asia . Deadly bushfires destroy hundreds of homes in Australia’s New South Wales Windstorm Christian moved across western and northern Europe, bringing hurricane-force wind gusts and torrential rains to several countries. At least 18 people were killed and dozens more were injured. The heaviest damage was sustained in the United Kingdom, France, Belgium, the Netherlands and Scandinavia, where a peak wind gust of 195 kph (120 mph) was recorded in Denmark. More than 1.2 million power outages were recorded and travel was severely disrupted throughout the continent. Reports from European insurers suggest that payouts are likely to breach EUR1.0 billion (USD1.35 billion). Total economic losses will be even higher. Christian becomes the costliest European windstorm since WS Xynthia in 2010. Cyclone Phailin became the strongest system to make landfall in India since 1999, coming ashore in the eastern state of Odisha. At least 46 people were killed. Tremendous rains, an estimated 3.5-meter (11.0-foot) storm surge, and powerful winds led to catastrophic damage to more than 430,000 homes and 668,000 hectares (1.65 million) acres of cropland. -

On the Extreme Rainfall of Typhoon Morakot (2009)
JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 116, D05104, doi:10.1029/2010JD015092, 2011 On the extreme rainfall of Typhoon Morakot (2009) Fang‐Ching Chien1 and Hung‐Chi Kuo2 Received 21 September 2010; revised 17 December 2010; accepted 4 January 2011; published 4 March 2011. [1] Typhoon Morakot (2009), a devastating tropical cyclone (TC) that made landfall in Taiwan from 7 to 9 August 2009, produced the highest recorded rainfall in southern Taiwan in the past 50 years. This study examines the factors that contributed to the heavy rainfall. It is found that the amount of rainfall in Taiwan was nearly proportional to the reciprocal of TC translation speed rather than the TC intensity. Morakot’s landfall on Taiwan occurred concurrently with the cyclonic phase of the intraseasonal oscillation, which enhanced the background southwesterly monsoonal flow. The extreme rainfall was caused by the very slow movement of Morakot both in the landfall and in the postlandfall periods and the continuous formation of mesoscale convection with the moisture supply from the southwesterly flow. A composite study of 19 TCs with similar track to Morakot shows that the uniquely slow translation speed of Morakot was closely related to the northwestward‐extending Pacific subtropical high (PSH) and the broad low‐pressure systems (associated with Typhoon Etau and Typhoon Goni) surrounding Morakot. Specifically, it was caused by the weakening steering flow at high levels that primarily resulted from the weakening PSH, an approaching short‐wave trough, and the northwestward‐tilting Etau. After TC landfall, the circulation of Goni merged with the southwesterly flow, resulting in a moisture conveyer belt that transported moisture‐laden air toward the east‐northeast. -

Capital Adequacy (E) Task Force RBC Proposal Form
Capital Adequacy (E) Task Force RBC Proposal Form [ ] Capital Adequacy (E) Task Force [ x ] Health RBC (E) Working Group [ ] Life RBC (E) Working Group [ ] Catastrophe Risk (E) Subgroup [ ] Investment RBC (E) Working Group [ ] SMI RBC (E) Subgroup [ ] C3 Phase II/ AG43 (E/A) Subgroup [ ] P/C RBC (E) Working Group [ ] Stress Testing (E) Subgroup DATE: 08/31/2020 FOR NAIC USE ONLY CONTACT PERSON: Crystal Brown Agenda Item # 2020-07-H TELEPHONE: 816-783-8146 Year 2021 EMAIL ADDRESS: [email protected] DISPOSITION [ x ] ADOPTED WG 10/29/20 & TF 11/19/20 ON BEHALF OF: Health RBC (E) Working Group [ ] REJECTED NAME: Steve Drutz [ ] DEFERRED TO TITLE: Chief Financial Analyst/Chair [ ] REFERRED TO OTHER NAIC GROUP AFFILIATION: WA Office of Insurance Commissioner [ ] EXPOSED ________________ ADDRESS: 5000 Capitol Blvd SE [ ] OTHER (SPECIFY) Tumwater, WA 98501 IDENTIFICATION OF SOURCE AND FORM(S)/INSTRUCTIONS TO BE CHANGED [ x ] Health RBC Blanks [ x ] Health RBC Instructions [ ] Other ___________________ [ ] Life and Fraternal RBC Blanks [ ] Life and Fraternal RBC Instructions [ ] Property/Casualty RBC Blanks [ ] Property/Casualty RBC Instructions DESCRIPTION OF CHANGE(S) Split the Bonds and Misc. Fixed Income Assets into separate pages (Page XR007 and XR008). REASON OR JUSTIFICATION FOR CHANGE ** Currently the Bonds and Misc. Fixed Income Assets are included on page XR007 of the Health RBC formula. With the implementation of the 20 bond designations and the electronic only tables, the Bonds and Misc. Fixed Income Assets were split between two tabs in the excel file for use of the electronic only tables and ease of printing. However, for increased transparency and system requirements, it is suggested that these pages be split into separate page numbers beginning with year-2021. -
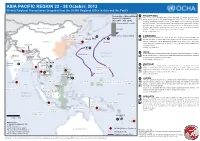
Pdf | 431.12 Kb
ASIA PACIFIC REGION 22 - 28 October, 2013 Weekly Regional Humanitarian Snapshot from the OCHA Regional Office in Asia and the Pacific 1 PHILIPPINES Probability of Above/Below As of 21 Oct, the 7.2M earthquake in Bohol had killed 186 people, affected some 3 Normal Precipitation r" million, and left nearly 381,000 people displaced of whom 70% or 271,000 were staying (Nov 2013 - Jan 2014) outside of established evacuation centers. These people were in urgent need of shelter Above normal rainfall and WASH support. Psycho-social support was identified as an urgent need for children traumatized by the earthquake, which has produced well over 2,000 aftershocks so far. Recently repaired bridges and roads have opened greater access to affected locations M O N G O L I A normal in Bohol. The Government has welcomed international assistance. Source: OCHA Sitrep No. 4 DPR KOREA Below normal rainfall 2 CAMBODIA 5 Floods across Cambodia have claimed 168 lives, displaced almost 145,000 and 5 RO KOREA JAPAN r" p" u" affected more than 1.7 million. Waters have begun to recede across the country with the worst affected provinces being Battambang and Banteay Meanchey, where many parts C H I N A LEKIMA KOBE remain flooded. Communities are in urgent need of clean water, basic sanitation and BHUTAN emergency shelter. NEPAL p" 5 Source: HRF Sitrep No. 4 KATHMANDU 3 INDIA PA C I F I C Heavy rainfall has been affecting the states of Andhra Pradesh and Odisha, SE India, in BANGLADESH FRANCISCO I N D I A u" the last few days. -

Indigenous Knowledge and Endogenous Actions for Building Tribal Resilience After Typhoon Soudelor in Northern Taiwan
sustainability Article Indigenous Knowledge and Endogenous Actions for Building Tribal Resilience after Typhoon Soudelor in Northern Taiwan Su-Hsin Lee 1 and Yin-Jen Chen 2,* 1 Department of Geography, National Taiwan Normal University, 162, Section 1, Heping E. Rd., Taipei City 10610, Taiwan; [email protected] 2 Graduate Institute of Earth Science, Chinese Culture University, 55, Hwa-Kang Road, Yang-Ming-Shan, Taipei City 11114, Taiwan * Correspondence: [email protected] Abstract: Indigenous peoples often face significant vulnerabilities to climate risks, yet the capacity of a social-ecological system (SES) to resilience is abstracted from indigenous and local knowledge. This research explored how the Tayal people in the Wulai tribes located in typhoon disaster areas along Nanshi River used indigenous knowledge as tribal resilience. It applied empirical analysis from secondary data on disaster relief and in-depth interviews, demonstrating how indigenous people’s endogenous actions helped during post-disaster reconstructing. With the intertwined concepts of indigenous knowledge, SESs, and tribes’ cooperation, the result presented the endogenous actions for tribal resilience. In addition, indigenous knowledge is instigated by the Qutux Niqan of mutual assistance and symbiosis among the Wulai tribes, and there is a need to build joint cooperation through local residence, indigenous people living outside of their tribes, and religious or social groups. The findings of tribal resilience after a typhoon disaster of co-production in the Wulai, Lahaw, and Fushan tribes include the importance of historical context, how indigenous people turn to their local knowledge rather than just only participating in disaster relief, and how they produce indigenous tourism for indigenous knowledge inheritance. -

The Impact of Dropwindsonde on Typhoon Track Forecasts in DOTSTAR and T-PARC
1 Eyewall Evolution of Typhoons Crossing the Philippines and Taiwan: An 2 Observational Study 3 Kun-Hsuan Chou1, Chun-Chieh Wu2, Yuqing Wang3, and Cheng-Hsiang Chih4 4 1Department of Atmospheric Sciences, Chinese Culture University, Taipei, Taiwan 5 2Department of Atmospheric Sciences, National Taiwan University, Taipei, Taiwan 6 3International Pacific Research Center, and Department of Meteorology, University of 7 Hawaii at Manoa, Honolulu, Hawaii 8 4Graduate Institute of Earth Science/Atmospheric Science, Chinese Culture University, 9 Taipei, Taiwan 10 11 12 13 14 Terrestrial, Atmospheric and Oceanic Sciences 15 (For Special Issue on “Typhoon Morakot (2009): Observation, Modeling, and 16 Forecasting Applications”) 17 (Accepted on 10 May, 2011) 18 19 ___________________ 20 Corresponding Author’s address: Kun-Hsuan Chou, Department of Atmospheric Sciences, 21 National Taiwan University, 55, Hwa-Kang Road, Yang-Ming-Shan, Taipei 111, Taiwan. 22 ([email protected]) 1 23 Abstract 24 This study examines the statistical characteristics of the eyewall evolution induced by 25 the landfall process and terrain interaction over Luzon Island of the Philippines and Taiwan. 26 The interesting eyewall evolution processes include the eyewall expansion during landfall, 27 followed by contraction in some cases after re-emergence in the warm ocean. The best 28 track data, advanced satellite microwave imagers, high spatial and temporal 29 ground-observed radar images and rain gauges are utilized to study this unique eyewall 30 evolution process. The large-scale environmental conditions are also examined to 31 investigate the differences between the contracted and non-contracted outer eyewall cases 32 for tropical cyclones that reentered the ocean. -

Downloaded 10/05/21 02:09 PM UTC 1426 WEATHER and FORECASTING VOLUME 29
DECEMBER 2014 W E I 1425 Surface Wind Nowcasting in the Penghu Islands Based on Classified Typhoon Tracks and the Effects of the Central Mountain Range of Taiwan CHIH-CHIANG WEI Department of Digital Content Designs and Management, Toko University, Pu-Tzu City, Chia-Yi County, Taiwan (Manuscript received 5 March 2014, in final form 21 September 2014) ABSTRACT The purposes of this study were to forecast the hourly typhoon wind velocity over the Penghu Islands, and to discuss the effects of the terrain of the Central Mountain Range (CMR) of Taiwan over the Penghu Islands based on typhoon tracks. On average, a destructive typhoon hits the Penghu Islands every 15–20 yr. As a typhoon approaches the Penghu Islands, its track and intensity are influenced by the CMR topography. Therefore, CMR complicates the wind forecast of the Penghu Islands. Six main typhoon tracks (classes I–VI) are classified based on typhoon directions, as follows: (I) the direction of direct westward movement across the CMR of Taiwan, (II) the direction of northward movement along the eastern coast of Taiwan, (III) the direction of northward movement traveling through Taiwan Strait, (IV) the direction of westward movement traveling through Luzon Strait, (V) the direction of westward movement traveling through the southern East China Sea (near northern Taiwan), and (VI) the irregular track direction. The adaptive network-based fuzzy inference system (ANFIS) and multilayer perceptron neural network (MLPNN) were used as the forecasting technique for predicting the wind velocity. A total of 49 typhoons from 2000 to 2012 were analyzed. Results showed that the ANFIS models provided high-reliability predictions for wind velocity, and the ANFIS achieved more favorable performance than did the MLPNN. -

Tropical Cyclones 2019
<< LINGLING TRACKS OF TROPICAL CYCLONES IN 2019 SEP (), !"#$%&'( ) KROSA AUG @QY HAGIBIS *+ FRANCISCO OCT FAXAI AUG SEP DANAS JUL ? MITAG LEKIMA OCT => AUG TAPAH SEP NARI JUL BUALOI SEPAT OCT JUN SEPAT(1903) JUN HALONG NOV Z[ NEOGURI OCT ab ,- de BAILU FENGSHEN FUNG-WONG AUG NOV NOV PEIPAH SEP Hong Kong => TAPAH (1917) SEP NARI(190 6 ) MUN JUL JUL Z[ NEOGURI (1920) FRANCISCO (1908) :; OCT AUG WIPHA KAJIK() 1914 LEKIMA() 1909 AUG SEP AUG WUTIP *+ MUN(1904) WIPHA(1907) FEB FAXAI(1915) JUL JUL DANAS(190 5 ) de SEP :; JUL KROSA (1910) FUNG-WONG (1927) ./ KAJIKI AUG @QY @c NOV PODUL SEP HAGIBIS() 1919 << ,- AUG > KALMAEGI OCT PHANFONE NOV LINGLING() 1913 BAILU()19 11 \]^ ./ ab SEP AUG DEC FENGSHEN (1925) MATMO PODUL() 191 2 PEIPAH (1916) OCT _` AUG NOV ? SEP HALONG (1923) NAKRI (1924) @c MITAG(1918) NOV NOV _` KALMAEGI (1926) SEP NAKRI KAMMURI NOV NOV DEC \]^ MATMO (1922) OCT BUALOI (1921) KAMMURI (1928) OCT NOV > PHANFONE (1929) DEC WUTIP( 1902) FEB 二零一 九 年 熱帶氣旋 TROPICAL CYCLONES IN 2019 2 二零二零年七月出版 Published July 2020 香港天文台編製 香港九龍彌敦道134A Prepared by: Hong Kong Observatory 134A Nathan Road Kowloon, Hong Kong © 版權所有。未經香港天文台台長同意,不得翻印本刊物任何部分內容。 © Copyright reserved. No part of this publication may be reproduced without the permission of the Director of the Hong Kong Observatory. 本刊物的編製和發表,目的是促進資 This publication is prepared and disseminated in the interest of promoting 料交流。香港特別行政區政府(包括其 the exchange of information. The 僱員及代理人)對於本刊物所載資料 Government of the Hong Kong Special 的準確性、完整性或效用,概不作出 Administrative Region