Compared with Other Externalities the Study of the Noise Impact on The
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Calendario Mano Parejas
XXVI. BIZKAIKO KLUBEN ARTEKO TXAPELKETA XXVI CAMPEONATO DE BIZKAIA DE CLUBES GRAN PREMIO EL CORTE INGLES MANO PAREJAS CADETE 1º ESKUZ BINAKA KADETE 1ª 25 Septiembre-Iraila LEA-ATXONDO DANOK LAGUNAK-OLGETAN “S” LAGUN ONAK-OLGETAN “M” OLGETAN “U”-IURRETA OLGETAN “A”-UPO MENDI “M” TXUMULUXUETA-KURENE UPO MEDI “I”-ERDU 2 Octubre-Urria UPO MENDI “M”-TXUMULUXUETA IURRETA-OLGETAN “A” OLGETAN “M”-OLGETAN “U” OLGETAN “S”-LAGUN ONAK ATXONDO-DANOK LAGUNAK ERDU-LEA KURENE-UPO MENDI “I” 9 Octubre-Urria DANOK LAGUNAK-ERDU LAGUN ONAK-ATXONDO OLGETAN “U”-OLGETAN “S” OLGETAN “A”-OLGETAN “M” TXUMULUXUETA-IURRETA KURENE-UPO MENDI “M” UPO MEDNI “I”-LEA 12 Octubre-Urria IURRETA-KURENE OLGETAN “M”-TXUMULUXUETA OLGETAN “S”-OLGETAN “A” ATXONDO-OLGETAN “U” ERDU-LAGUN ONAK LEA-DANOK LAGUNAK UPO MEDI “M”-UPO MENDI “I” 16 Octubre-Urria LAGUN ONAK-LEA OLGETAN “U”-ERDU OLGETAN “A”-ATXONDO TXUMULUXUETA-OLGETAN “S” KURENE-OLGETAN “M” UPO MENDI “M”-IURRETA UPO MEDNI “I”-DANOK LAGUNAK 23 Octubre-Urria OLGETAN “M”-UPO MENDI “M” OLGETAN “S”-KURENE ATXONDO-TXUMULUXUETA ERDU-OLGETAN “A” LEA-OLGETAN “U” DANOK LAGUNAK-LAGUN ONAK IURRETA-UPO MENDI “I” 30 Octubre-Urria OLGETAN “U”-DANOK LAGUNAK OLGETAN “A”-LEA TXUMULUXUETA-ERDU KURENE-ATXONDO UPO MENDI “M”-OLGETAN “S” IURRETA-OLGETAN “M” UPO MEDI “I”-LAGUN ONAK 2 Noviembre-Azaroa OLGETAN “S”-IURRETA ATXONDO-UPO MENDI “M” ERDU-KURENE LEA-TXUMULUXUETA DANOK LAGUNAK-OLGETAN “A” LAGUN ONAK-OLGETAN “U” OLGETAN “M”-UPO MENDI “I” 6 Noviembre-Azaroa OLGETAN “A”-LAGUN ONAK TXUMULUXUETA-DANOK LAGUNAK KURENE-LEA UPO MENDI “M”-ERDU IURRETA-ATXONDO -

Adobe Photoshop
plandeacción territorial deabastecimiento de laReservade laBiosfera deUrdaibai documento nº4: estudio de las directrices de organización y gestión de la ejecución enero2018ko urtarrila Índice de documentos Documento nº 1: Memoria informativa y justificativa Documento nº 2: Planos de información Documento nº 3: Planos de ordenación de las nuevas infraestructuras Documento nº 4: Estudio de las directrices de organización y gestión de la ejecución Documento nº 5: Normativa Documento nº 6: Estudio de viabilidad económico-financiera Documento nº 7: Estudio de afección al paisaje y regulación para la implantación Índice de documetos 1 DOCUMENTO Nº 4 Estudio de las directrices de organización y gestión de la ejecución Índice 1 Introducción 1 2 Situación actual 2 3 Escenario a corto plazo 4 4 Escenario a medio plazo 6 5 Escenario a largo plazo 8 Estudio de las directrices de organización y gestión de la ejecución i 1 Introducción En el presente Plan de Acción Terrritorial de Abastecimiento de la Reserva de la Biosfera de Urdaibai se proponen una serie de actuaciones dirigidas a solucionar los problemas de falta de caudales ecológicos por escasez de recurso en momentos de estiaje, así como una falta de garantía en el suministro al abastecimiento y una situación de vulnerabilidad extrema del sistema por problemas de contaminación. Las actuaciones propuestas se pueden agrupar del siguiente modo: Actuaciones relacionadas con una mejora de la gestión Otras actuaciones ya previstas por la Administración competente Actuaciones necesarias para reducir definitivamente el déficit y aumentar el recurso disponible Para el tercer grupo de actuaciones se ha desarrollado un análisis multicriterio de varias alternativas. -

Bizkaiko Foru Aldundiaren Eta Durangoko
Bizkaiko Foru Aldundiaren eta Durangoko Convenio de colaboración entre la Diputación Foral Merinaldearen Amakomunazgoaren eta Abadiño, de Bizkaia, la Mancomunidad de la Merindad de Amorebieta Etxano, Atxondo, Berriz, Durango, Durango y los Ayuntamientos de Abadiño, Elorrio, Ermua, Garai, Iurreta, Izurtza, Mallabia, Amorebieta Etxano, Atxondo, Berriz, Durango, Mañaria eta Zaldibarko Udalen arteko lankidetza- Elorrio, Ermua, Garai, Iurreta, Izurtza, Mallabia, hitzarmena, 2020 urterako, gazteriaren arloko Mañaria y Zaldibar para la implantación, impulso y politika integrala ezarri, bultzatu eta garatzeko. desarrollo de políticas integrales de juventud, durante el año 2020. HAUEK BILTZEN DIRA SE REUNEN Alde batetik, Unai Rementeria Maiz jauna, De una parte, D. Unai Rementeria Maiz, Diputado Bizkaiko Ahaldun Nagusia, Bizkaiko Foru General de Bizkaia, en nombre y representación Aldundiaren izenean jarduten duena, Bizkaiko de la misma, en virtud de las facultades atribuidas Kondaira Lurraldeko Foru Erakundeen Hautapen, por la Norma Foral 3/1987 de 13 de febrero, de Antolaketa, Erregimen eta Funtzionamenduari Elección, Organización, Régimen y buruzko otsailaren 13ko 1987/3 Foru Arauaren Funcionamiento de las Instituciones Forales del 23.1. artikuluan xedaturikoa eta foru arau Territorio Histórico de Bizkaia. horretako 28 c) artikuluan emandako ahalmenak direla bide. Bestetik, De otra parte, Mireia Elkoroiribe Zenikaonandia andrea, Dña. Mireia Elkoroiribe Zenikaonandia Presidenta Durangoko Merinaldearen Amakomunazgoko de la Mancomunidad de la Merindad de Durango, presidentea (IFZ: P 4800001 B), haren izenean eta en nombre y representación de la misma, NIF P ordezkaritzan, helbidea Abadiñoko Astola Kaleko 4800001 B, con domicilio en Abadiño, calle Astola, 26 zk.an duena, Mankomunitateko estatutuetan 26 en virtud de las competencias atribuidas en los emandako eskumenak direla bide. -

Corpus Based Prosodic Variation in Basque: Y/N Questions Marked with the Particle Al
CORPUS BASED PROSODIC VARIATION IN BASQUE: Y/N QUESTIONS MARKED WITH THE PARTICLE AL VARIACIÓN PROSÓDICA EN VASCO BASADA EN CORPUS: PREGUNTAS SÍ/NO MARCADAS CON LA PARTÍCULA AL GOTZON AURREKOETXEA Universidad del País Vasco [email protected] IÑAKI GAMINDE Universidad del País Vasco [email protected] AITOR IGLESIAS Universidad del País Vasco [email protected] Artículo recibido el día: 8/11/2010 Artículo aceptado definitivamente el día: 13/07/2011 Estudios de Fonética Experimental, ISSN 1575-5533, XX, 2011, pp. 11-31 Corpus based prosodic variation in Basque: Y/N questions... 13 ABSTRACT This paper describes the intonational variation between two generations in three different localities of the Basque Country, using data recorded and organized in the EDAK corpus (Dialectal Oral Corpus of the Basque Language) and analysing the usage of just one type of sentence, namely y/n questions. In the selected localities, there are two morphological ways of constructing this type of sentence: using the morphological marker al before the verb (or between the verb and the auxiliary) or not using it. First, we identify the phonological patterns that exist in these localities. Then, we analyse intergenerational variation, according to the five different phonological patterns found. Finally, we study the geo-prosodic variation which exists between older and younger people from these localities. Keywords: linguistic corpus, Basque language, prosody, socio-prosodic variation, geo-prosodic variation. RESUMEN El artículo trata la variación entonacional entre dos generaciones en tres localidades distintas situadas en el centro del espacio lingüístico vasco en frases interro-gativas absolutas con datos del EDAK (Corpus dialectal oral del euskera). -

Enpresa-Ideien Lehiaketa / Concurso De Ideas De Negocio
Enpresa-ideien lehiaketa / Concurso de ideas de negocio 1. Sarrera 1. Introducción Bizkaiko Foru Aldundiak, bere helburuen artean, La Diputación Foral de Bizkaia tiene entre sus gazteei zuzendutako zerbitzuak eta jarduerak objetivos el de promocionar los servicios y sustatzea eta gazte politika integralak gauzatzeko actuaciones dirigidas a los jóvenes y posibilitar la aukerak ahalbidetzea ditu, «Gaztedi Bizkaia ejecución de políticas integrales de juventud, 2020» proiektuan jasotako konpromisoak lortzera llevando a efecto las medidas tendentes a la bideratutako neurriak aurrera eramanez. consecución de los compromisos recogidos en el Aipatutako helburua kontuan hartuta, Aldundiak «Proyecto Gaztedi Bizkaia». Teniendo presente Tokiko Erakundeen bitartez hiritarrengana heltzea dicho objetivo la Diputación ha creído beharrezkoa ikusten du, erakunde hauek direlako imprescindible incidir en el ámbito local, puesto hurbilenak. que sus instituciones son las que más cerca se encuentran de la ciudadanía. Testuinguru honetan, kasu bakoitzean En este contexto surge en el «Proyecto Gaztedi beharrezko zerbitzuak emanez, tokiko eremuan Bizkaia» de la Diputación Foral de Bizkaia que gaztedi politikak abian jarri nahi duen Bizkaiko busca poner en marcha políticas de juventud en Foru aldundiaren “Bizkaiko Gaztedi Plana” el ámbito local proporcionando los servicios agertzen da. Esku-hartzeko arlo nagusiak zortzi necesarios en cada caso. Las principales áreas dira: hezkuntza eta prestakuntza, enplegua eta de actuación son ocho: educación y formación, ekintzailetza, gizarte esku-hartzea, parte-hartzea empleo y emprendimiento, intervención social, eta nazioartekotzea. salud y bienestar, cultura y creatividad, compromiso social, participación e internacionalización. Proiektu hau koordinatutako era batean Para poder gestionar de manera coordinada este kudeatzeko Foru aldundiak gazte-eremuan proyecto la Diputación Foral de Bizkaia creó Bizkaiko udalak biltzen duen “Udal Gaztedi” sortu «Udal Gaztedi» que reúne en el ámbito juvenil a zuen. -

Spain-France Electricity Interconnection Across the Bay of Biscay
Spain-France electricity interconnection across the Bay of Biscay The sole responsibility of this publication lies with the author. The European Union is not responsible for any use that may be made of the information contained therein. Contents Electricity interconnection across the Bay of Biscay 2 • Project presentation 2 • What are the international interconnections? 3 - Advantages of interconnections 4 - Interconnections in Spain 5 • Energy planning 7 - Energy Plan 2015-2020 7 - Strategic environmental assessment 8 • Companies involved 10 • Main project characteristics 10 - Converter station (CS) 11 - Connecting power lines 12 - Underground cable 14 - Submarine cable 15 • Project timetable 15 The territory 16 • Scope of land study 16 • Scope of marine study 18 Description of alternative solutions 19 • Converter Station (CS) site 19 • Location of the beach joint 20 • Converter-landfall point connecting power lines 20 • Underwater cable 22 Significant impacts 23 Public participation 27 Additional information 33 2 Spain-France electricity interconnection across the Bay of Biscay www.ree.es 3 Electricity The new submarine interconnection between interconnection Spain and France across the across the Bay Bay of Biscay was designated as a “Project of Common of Biscay Interest”, due to its strategic nature, by the European Project presentation Commission and Parliament on 14 October 2013. This project consists of creating an electricity interconnection across the Bay of Biscay between the French electricity grid, from one of its substations, located to the north of the city of Bordeaux, and the Spanish electricity grid, through the Gatika substation, located in Biscay. system, as well as being considered one of the most important means for integrating the ambitious plans for renewable energy. -

Adaptación Antenas Colectivas De La
Últimas semanas para realizar la adaptación en Vizcaya CUENTA ATRÁS PARA FINALIZAR LA ADAPTACIÓN DE LAS ANTENAS COLECTIVAS DE TDT EN 112 MUNICIPIOS El próximo 11 de febrero algunos canales de TDT dejarán de emitir en sus antiguas frecuencias en 7 municipios, mientras que en el resto de la provincia cesarán las emisiones el 3 de marzo. Solo en el *51% de los edificios comunitarios de la provincia se han realizado ya las adaptaciones necesarias para seguir disfrutando de la oferta completa de TDT a partir de estas fechas Los administradores de fincas o presidentes de comunidades de propietarios deben contactar lo antes posible con una empresa instaladora registrada Además, a partir de la fecha de cese de emisiones de cada municipio, todos los ciudadanos de Vizcaya deberán resintonizar el televisor con su mando a distancia Toda la información sobre el cambio de frecuencias de la TDT está disponible en la página web www.televisiondigital.es y a través de los números de atención telefónica 901 20 10 04 y 91 088 98 79 Vitoria-Gasteiz, 21 de enero de 2020. Cuenta atrás para el cambio de frecuencias de la Televisión Digital Terrestre (TDT) en Vizcaya. A partir del próximo 11 de febrero, algunos canales estatales y autonómicos dejarán de emitir a través de sus antiguas frecuencias en Amoroto, Berriatua, Ea, Ispaster, Lekeitio, Mendexa y Ondarroa, mientras que en otros 105 municipios del resto de la provincia, incluida la capital, lo harán el 3 de marzo. Solo en el *51% de los aproximadamente 27.300 edificios comunitarios de tamaño mediano y grande de la provincia -que deben adaptar su instalación de antena colectiva- se ha realizado esta adaptación. -

Natural Beauty Spots Paradises to Be Discovered
The Active OUTDOORS Natural Beauty Spots Paradises to be discovered Walking and biking in Basque Country Surfing the waves Basque Coast Geopark Publication date: April 2012 Published by: Basquetour. Basque Tourism Agency for the Basque Department of Industry, Innovation, Commerce and Tourism Produced by: Bell Communication Photographs and texts: Various authors Printed by: MCC Graphics L.D.: VI 000-2011 The partial or total reproduction of the texts, maps and images contained in this publication without the San Sebastián express prior permission of the publisher and the Bilbao authors is strictly prohibited. Vitoria-Gasteiz All of the TOP experiences detailed in TOP in this catalogue are subject to change and EXPE RIEN may be updated. Therefore, we advise you CE to check the website for the most up to date prices before you book your trip. www.basquecountrytourism.net The 24 Active OUT- DOORS 20 28LOCAL NATURE SITES 6 Protected Nature Reserves Your gateway to Paradise 20 Basque Country birding Bird watching with over 300 species 24 Basque Coast Geopark Explore what the world way 6 34 like 60 million years ago ACTIVITIES IN THE BASQUE COUNTRY 28 Surfing Surfing the Basque Country amongst the waves and mountains 34 Walking Walking the Basque Country Cultural Landscape Legacy 42 42 Biking Enjoy the Basque Country's beautiful bike-rides 48 Unmissable experiences 51 Practical information Gorliz Plentzia Laredo Sopelana THE BASQUE Castro Urdiales Kobaron Getxo ATXURI Pobeña ITSASLUR Muskiz GREENWAY GREENWAY Portugalete ARMAÑÓN Sondika COUNTRY'S MONTES DE HIERRO Gallarta Sestao NATURAL PARK GREENWAY Ranero BILBAO La Aceña-Atxuriaga PROTECTED Traslaviña Balmaseda PARKS AND AP-68 Laudio-Llodio RESERVES Amurrio GORBEIA NATURAL PARK Almost 25% of Basque Country Orduña territory comprises of protected nature areas: VALDEREJO A Biosphere Reserve, nine AP-68 NATURAL PARK Natural Parks, the Basque Lalastra Coast Geopark, more than Angosto three hundred bird species, splendid waves for surfing and Zuñiga Antoñana numerous routes for walking or biking. -

Basques in the Americas from 1492 To1892: a Chronology
Basques in the Americas From 1492 to1892: A Chronology “Spanish Conquistador” by Frederic Remington Stephen T. Bass Most Recent Addendum: May 2010 FOREWORD The Basques have been a successful minority for centuries, keeping their unique culture, physiology and language alive and distinct longer than any other Western European population. In addition, outside of the Basque homeland, their efforts in the development of the New World were instrumental in helping make the U.S., Mexico, Central and South America what they are today. Most history books, however, have generally referred to these early Basque adventurers either as Spanish or French. Rarely was the term “Basque” used to identify these pioneers. Recently, interested scholars have been much more definitive in their descriptions of the origins of these Argonauts. They have identified Basque fishermen, sailors, explorers, soldiers of fortune, settlers, clergymen, frontiersmen and politicians who were involved in the discovery and development of the Americas from before Columbus’ first voyage through colonization and beyond. This also includes generations of men and women of Basque descent born in these new lands. As examples, we now know that the first map to ever show the Americas was drawn by a Basque and that the first Thanksgiving meal shared in what was to become the United States was actually done so by Basques 25 years before the Pilgrims. We also now recognize that many familiar cities and features in the New World were named by early Basques. These facts and others are shared on the following pages in a chronological review of some, but by no means all, of the involvement and accomplishments of Basques in the exploration, development and settlement of the Americas. -

Dossier WC2020 EUS V1
2020 ABENTURA ERRELEBOAK 226KM EGUNA Challenge GAUA NONSTOP BILBAO ERRELEBO EKAINAKJUNIO LASTERKETA ITZELA TALDE MIXTOAK wopchallenge.comBIZKAIAN ZEHAR 6- Gainera neuroendekapenezko gaixotasunen aurka borrokatzeko minutuak GEOLOCALIZAZIOA 7 ORIENTAZIOA ASFALTOA sortuko ditugu The Walk On Project Fundazioaren bidez IZEN EMATEA ETA INFO GUZTIA TRAIL RUNNING TEAM BUILDING TALDE ERRONKA @wopchallenge ALGORTAKO PORTU ARMINTZA ZAHARRA GALDAMES BARRIKA GALLARTA BAKIO ChallengeBILBAO ZORROTZA BILBAO BERMEO MURUETA SODUPE KORTEZUBI ARRIGORRIAGA AULESTI OIZ MENDIA LEGENDA ERMITABARRI Distantzia DIMA Zailtasuna Igoera desnibela MATIENA Jaitsiera desnibela Asfaltoa Trail URKIOLA Mixtoa Etapa Mota Interes puntua 1 ARRIGORRIAGA ChallengeBILBAO BUIA BILBAO ARRIGORRIAGA LA PEÑA 11Km Erraza 194 m GUGGENHEIM BILBAO MUSEOA 142 m 0m 200m 2 ERMITABARRI ChallengeBILBAO ARRIGORRIAGA ERMITABARRI 11,5Km Oso Gogorra 486 m 388 m ARRIGORRIAGA 0m 500m 3 DIMA IGORRE ChallengeBILBAO ERMITABARRI ARÁNZAZU DIMA 9,2Km Gogorra 185 m 221 m ERMITABARRI 0m 300m URKIOLAKO 4 SANTUTEGIA URKIOLA ChallengeBILBAO DIMA URKIOLA BALTZOLAKO KOBAZULOAK 14,8Km INDUSI Oso Gogorra 791 m 191 m DIMA 0m 900m 5 MATIENA ChallengeBILBAO URKIOLA MATIENA MENDIOLA 15,6Km ANBOTO HIRU GURUTZEN Erraza BEGIRATOKIA 206 m 808 m URKIOLA 900m 0m 6 MATIENA OIZ MENDIA OIZ MENDIA ChallengeBILBAO 13,1Km Gogorra GARAI 708 m 46 m MATIENA 800m 0m 7 AULESTI ChallengeBILBAO OIZ MENDIA AULESTI MUNITIBAR 13,8KmMUNITIBAR Erraza 100 m 793 m OIZ MENDIA 800m 0m 8 KORTEZUBI SANTIMAMIÑEKO KOBAZULOA ChallengeBILBAO OMAKO -

Excursiones 2020 Domingos
EXCURSIONES 2020 DOMINGOS Nº Día Recorrido GPS Km Hora SALIDA EUSCALDUNA-ZORROZA-SODUPE-LA HERRERA-BALMASEDA-LA HERBOSA-ARTZENTALES-SOPUERTA-MUSKIZ-EL HAYA-COBARON-POBEÑA-BIDEGORRI- 1 1 FEBRERO GPS 83 9:00 SABADO TRAPAGA-ZORROZA-BILBAO SALIDA AYUNTAMIENTO BILBAO-GALDAKAO-ERLETXES-LARRABETZU-MORGA-GEREKIZ-MUNGIA-MARURI-ANDRAKAS-LEMONIZ-GORLIZ-URDULIZ-UPV- 2 2 FEBRERO GPS 83 9:00 DOMINGO ASTRABUDUA-BILBAO- 3 8 FEBRERO SALIDA-EUSKALDUNA-LUTXANA-LAURO-MUNGIA-ARRIETA-RIGOITIA-GERNIKA-MUGICA-GEREKIZ-MORGA-LARRABETZU-LEZAMA-ASUA-BILBAO GPS 82 9:00 SABADO SALIDA AYUNTAMIENTO BILBAO-GALDAKAO-ARKOTXA-ZARATAMO-ARRIGORRIAGA-UGAO-ZEBERIO-SARASOLA-ARTEA-IGORRE-LEMOA-AMOREBIETA-ERLETXES-EL 4 9 FEBRERO GPS 81 9:00 DOMINGO GALLO-SUBIDA GANGUREN-ARTXANDA-ENEKURI-DEUSTO-BILBAO 5 15 FEBRERO SALIDA-EUSKALDUNA-ZORROZA-ZALLA-OTXARAN-LA HERBOSA-SOPUERTA-SAN ESTEBAN-HUMARAN-GUEÑES-SODUPE-BILBAO GPS 76 9:00 SABADO SALIDA AYUNTAMIENTO BILBAO-ZORROZA-SODUPE-GORDEXOLA-SAN COSME-ARANGUREN-ZALLA-AVELLANEDA-MERCADILLO-EL VENTORRO-SANTE LICES-CENTRO 6 16 FEBRERO GPS 84 9:00 DOMINGO INTERPRETACION DE PEÑAS NEGRAS -TRIANO-SAN MIGUEL-EL CASAL-ORTUELLA-TRAPAGA-ZORROZA-BILBAO- 22 FEBRERO GPS 9:00 SABADO MARCHA CLONICA OTXOA 7 22 FEBRERO SALIDA-EUSKALDUNA-LUTXANA-LAURO-GATIKA-ANDRAKAS-ARMINTZA-JATA-BAKIO-EMERALDO-MUNGIA-ARTEBAKARRA-ASUA-LUTXNA BILBO GPS 80 9:00 SABADO SALIDA AYUNTAMIENTO BILBAO-APERRIBAI-ARRIGORRIAGA-UGAO-ZEBERIO-SARASOLA-ARTEA-IGORRE-LEMOA-BEDIA-EL GALLO-ERLETXES-LARRETZU-ASTOREKA- 8 23 FEBRERO GPS 95 9:00, DOMINGO GAMIZ FIKA-MUNGIA-GATIKA-BUTRON-URDULIZ-UNBE-ASUA-LUTXANA-BILBAO -
Cadenza Document
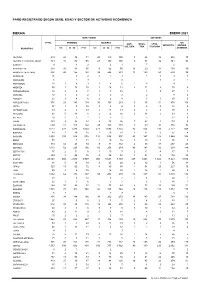
PARO REGISTRADO SEGÚN SEXO, EDAD Y SECTOR DE ACTIVIDAD ECONÓMICA BIZKAIA ENERO 2021 SEXO Y EDAD SECTORES TOTAL HOMBRES MUJERES SIN AGRI- INDUS- CONS- SERVICIOS EMPLEO CULTURA TRIA TRUCCIÓN MUNICIPIOS <25 25 - 44 >=45 <25 25 - 44 >=45 ANTERIOR ABADIÑO 414 24 74 71 25 115 105 3 96 18 258 39 ABANTO Y CIERVANA-ABANT 744 41 142 185 28 150 198 9 84 92 461 98 AJANGIZ 9 4 2 2 1 7 2 ALONSOTEGI 238 10 44 58 9 62 55 16 20 18 145 39 AMOREBIETA-ETXANO 898 44 155 188 34 246 231 13 149 50 592 94 AMOROTO 16 3 2 1 7 3 1 3 9 3 ARAKALDO 6 1 3 2 3 2 1 ARANTZAZU 18 1 4 3 1 4 5 1 8 9 AREATZA 56 1 15 10 1 18 11 2 11 5 30 8 ARRANKUDIAGA 38 3 4 7 1 7 16 3 5 27 3 ARRATZU 12 1 2 2 1 4 2 2 8 2 ARRIETA 21 3 4 6 2 2 4 3 3 10 5 ARRIGORRIAGA 737 28 143 154 36 157 219 9 95 51 478 104 ARTEA 37 1 5 16 3 6 6 3 6 4 18 6 ARTZENTALES 49 2 8 13 2 11 13 2 3 8 30 6 ATXONDO 61 5 18 8 2 12 16 3 18 3 33 4 AULESTI 18 4 4 1 1 4 4 3 11 4 BAKIO 149 3 32 43 2 33 36 7 23 4 110 5 BALMASEDA 604 17 100 122 24 150 191 9 69 36 395 95 BARAKALDO 7.013 273 1.293 1.624 277 1.692 1.854 94 604 710 4.777 828 BARRIKA 89 2 19 25 2 19 22 2 11 5 67 4 BASAURI 2.950 109 524 638 116 656 907 43 347 228 1.944 388 BEDIA 55 7 11 2 19 16 3 10 3 36 3 BERANGO 333 12 45 74 9 81 112 2 30 18 257 26 BERMEO 1.010 52 225 196 42 256 239 49 143 66 608 144 BERRIATUA 37 2 11 6 1 10 7 2 11 4 17 3 BERRIZ 204 8 44 38 4 56 54 3 51 5 116 29 BILBAO 25.341 986 4.656 5.909 950 5.651 7.189 488 1.948 1.926 17.423 3.556 BUSTURIA 88 5 16 19 3 25 20 2 12 4 56 14 DERIO 323 13 62 72 8 80 88 1 54 25 227 16 DIMA 55 3 6 15 16 15 1 12 1 36