Quantized Melodic Contours in Indian Art Music Perception: Application to Transcription
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
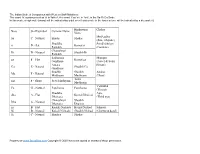
Note Staff Symbol Carnatic Name Hindustani Name Chakra Sa C
The Indian Scale & Comparison with Western Staff Notations: The vowel 'a' is pronounced as 'a' in 'father', the vowel 'i' as 'ee' in 'feet', in the Sa-Ri-Ga Scale In this scale, a high note (swara) will be indicated by a dot over it and a note in the lower octave will be indicated by a dot under it. Hindustani Chakra Note Staff Symbol Carnatic Name Name MulAadhar Sa C - Natural Shadaj Shadaj (Base of spine) Shuddha Swadhishthan ri D - flat Komal ri Rishabh (Genitals) Chatushruti Ri D - Natural Shudhh Ri Rishabh Sadharana Manipur ga E - Flat Komal ga Gandhara (Navel & Solar Antara Plexus) Ga E - Natural Shudhh Ga Gandhara Shudhh Shudhh Anahat Ma F - Natural Madhyam Madhyam (Heart) Tivra ma F - Sharp Prati Madhyam Madhyam Vishudhh Pa G - Natural Panchama Panchama (Throat) Shuddha Ajna dha A - Flat Komal Dhaivat Dhaivata (Third eye) Chatushruti Shudhh Dha A - Natural Dhaivata Dhaivat ni B - Flat Kaisiki Nishada Komal Nishad Sahsaar Ni B - Natural Kakali Nishada Shudhh Nishad (Crown of head) Så C - Natural Shadaja Shadaj Property of www.SarodSitar.com Copyright © 2010 Not to be copied or shared without permission. Short description of Few Popular Raags :: Sanskrut (Sanskrit) pronunciation is Raag and NOT Raga (Alphabetical) Aroha Timing Name of Raag (Karnataki Details Avroha Resemblance) Mood Vadi, Samvadi (Main Swaras) It is a old raag obtained by the combination of two raags, Ahiri Sa ri Ga Ma Pa Ga Ma Dha ni Så Ahir Bhairav Morning & Bhairav. It belongs to the Bhairav Thaat. Its first part (poorvang) has the Bhairav ang and the second part has kafi or Så ni Dha Pa Ma Ga ri Sa (Chakravaka) serious, devotional harpriya ang. -

1. Father's Name of Acharya KCD Brihaspati
A 1 1. Father's name of Acharya K.C.D. Brihaspati was : (1) Pt. Datt Ram (2) Shri Niwas (3) Pt. Ayodhya Prasad (4) Shri Govind Ram vkpk;Z dSyk'k panz nso c`gLifr ds firk uke Fkk % (1) iafMr nÙk jke (2) Jhfuokl (3) iafMr v;ks/;k izlkn (4) iafMr xksfoan jke 2. How many Talis are in Teental ? (1) 4 (2) 2 (3) 3 (4) 5 rhurky eas fdruh rkyh gS % (1) 4 (2) 2 (3) 3 (4) 5 3. Who is the writer of Sangeet Chintamani ? (1) Pt. Bhatkhande (2) K.C.D. Brihaspati (3) V. D. Paluskar (4) None of them laxhr fparkef.k iqLrd ds ys[kd dkSu gS \ (1) iafMr Hkkr[kaMs (2) dSyk'k panz nso c`gLifr (3) oh0 Mh0 iyqLdj (4) buesa ls dksbZ ugha 4. Which is birth place of Lal Mani Mishra ? (1) Kanpur (2) Delhi (3) Jaipur (4) Agra ykyef.k feJ dk tUe LFkku dkSu&lk gS \ (1) dkuiqj (2) fnYyh (3) t;iqj (4) vkxjk 94466/(A) P. T. O. 2 A 5. Which is Sandhiprakash Raga ? (1) Puriya Dhanashree (2) Bhimplasi (3) Todi (4) None of them dkSu&lk laf/kizdk'k jkx gS \ (1) iwfj;k /kukJh (2) Hkheiyklh (3) rksM+h (4) buesa ls dksbZ ugha 6. Who created Raga Todi ? (1) Amir Khusrao (2) Tansen (3) Baiju Bawara (4) Lal Mani Mishra jkx rksM+h dh jpuk fdlus dh \ (1) vehj [kqljks (2) rkulsu (3) cStw ckojk (4) ykyef.k feJ 7. Ashrya Raga of Todi Thata is : (1) Multani (2) Todi (3) Gujari Todi (4) Bhupal Todi rksM+h FkkV dk vkJ; jkx gS % (1) eqYrkuh (2) rksM+h (3) xqtjh rksM+h (4) Hkksiky rksM+h 8. -

Track Name Singers VOCALS 1 RAMKALI Pt. Bhimsen Joshi 2 ASAWARI TODI Pt
Track name Singers VOCALS 1 RAMKALI Pt. Bhimsen Joshi 2 ASAWARI TODI Pt. Bhimsen Joshi 3 HINDOLIKA Pt. Bhimsen Joshi 4 Thumri-Bhairavi Pt. Bhimsen Joshi 5 SHANKARA MANIK VERMA 6 NAT MALHAR MANIK VERMA 7 POORIYA MANIK VERMA 8 PILOO MANIK VERMA 9 BIHAGADA PANDIT JASRAJ 10 MULTANI PANDIT JASRAJ 11 NAYAKI KANADA PANDIT JASRAJ 12 DIN KI PURIYA PANDIT JASRAJ 13 BHOOPALI MALINI RAJURKAR 14 SHANKARA MALINI RAJURKAR 15 SOHONI MALINI RAJURKAR 16 CHHAYANAT MALINI RAJURKAR 17 HAMEER MALINI RAJURKAR 18 ADANA MALINI RAJURKAR 19 YAMAN MALINI RAJURKAR 20 DURGA MALINI RAJURKAR 21 KHAMAJ MALINI RAJURKAR 22 TILAK-KAMOD MALINI RAJURKAR 23 BHAIRAVI MALINI RAJURKAR 24 ANAND BHAIRAV PANDIT JITENDRA ABHISHEKI 25 RAAG MALA PANDIT JITENDRA ABHISHEKI 26 KABIR BHAJAN PANDIT JITENDRA ABHISHEKI 27 SHIVMAT BHAIRAV PANDIT JITENDRA ABHISHEKI 28 LALIT BEGUM PARVEEN SULTANA 29 JOG BEGUM PARVEEN SULTANA 30 GUJRI JODI BEGUM PARVEEN SULTANA 31 KOMAL BHAIRAV BEGUM PARVEEN SULTANA 32 MARUBIHAG PANDIT VASANTRAO DESHPANDE 33 THUMRI MISHRA KHAMAJ PANDIT VASANTRAO DESHPANDE 34 JEEVANPURI PANDIT KUMAR GANDHARVA 35 BAHAR PANDIT KUMAR GANDHARVA 36 DHANBASANTI PANDIT KUMAR GANDHARVA 37 DESHKAR PANDIT KUMAR GANDHARVA 38 GUNAKALI PANDIT KUMAR GANDHARVA 39 BILASKHANI-TODI PANDIT KUMAR GANDHARVA 40 KAMOD PANDIT KUMAR GANDHARVA 41 MIYA KI TODI USTAD RASHID KHAN 42 BHATIYAR USTAD RASHID KHAN 43 MIYA KI TODI USTAD RASHID KHAN 44 BHATIYAR USTAD RASHID KHAN 45 BIHAG ASHWINI BHIDE-DESHPANDE 46 BHINNA SHADAJ ASHWINI BHIDE-DESHPANDE 47 JHINJHOTI ASHWINI BHIDE-DESHPANDE 48 NAYAKI KANADA ASHWINI -

Scheme of Exmination for the Session 2012-13 Ba-I (Music
1 SCHEME OF EXMINATION FOR THE SESSION 2012-13 BA-I (MUSIC VOCAL) Semester-I for the session 2012-13 M.M.100 20% Internal Assessment 5% for attendance 10% for unannounced test 5% for assignment Paper-I Theory- Fundamental Study of Music M.M.30 3hrs. Semester-II Semester-I for the session 2012-13 M.M.100 20% Internal Assessment 5% for attendance 5% for unannounced test 10% for assignment Paper-II Theory- - Fundamental Study of Music M.M.30 3hrs Paper-III Practical (Stage-Performance & Viva-Voce) M.M.100 2 Scheme of Examination of BA-I (Vocal) for semester system w.e.f. academic year 2012-13 Ist Semester 20% Internal Assessment 5% for attendance 10% for unannounced test 5% for assignment Theory Paper-I Theory MM.30 Note: 1 Que. 1 consisting of 6 Numbers of short type question (having no internal choice) spread over the whole syllabus should be compulsory. Note: 2 1. Question I consisting of (preferably 6 question having no internal choice) spread over the whole syllabi should be compulsory. 2. The Syllabus is divided into 3 units. Candidate is required to attempt three questions selecting one question from each unit and fourth question can be selected from any unit. The Examiner should set 8 questions (Unit 1-3 questions, Unit 2- 3questions and Unit 3- 2questions) from the 3 unit and the candidate will be required to attempt 4 questions from the three units. 3. The candidate should attempt 5 questions in all including 1 compulsory question. Section –A 1. Notation of three Drut Khayals in the following Ragas: a) Yaman b) Alhaiya Bilawal c) Kafi 2. -

Sitar) Course Subject Papers Papers Code Time Credits External Internal Total (Hours/Week) Category Marks L+T+P
Kurukshetra University, Kurukshetra M. A. Music Credits According to CBCS in the Course Structure w.e.f 2016-17 1 credit =25 marks , the value of L+T+P is = 1+1+2 1 lecture = 1 credit, 1 Tutorial = 1 Credit, 2 Practical = 1 Credit M.A. Ist SEMESTER (Sitar) Course Subject Papers papers Code Time Credits External Internal Total (Hours/Week) Category Marks L+T+P M.A. Sitar Core-1 General and MMU411 3 hours 4 80 20 100 4+0+0 Applied Music Theory Core-2 History of Indian MMU412 3 hours 4 80 20 100 4+0+0 music Core-3 Stage performance MMUS413 35 to 45 min 4 80 20 100 0+0+8 Core-4 Viva –Voce & MMUS414 35 to 45 min 4 80 20 100 0+0+8 Comparative Study of Raga Core-5 Lecture MMUS415 35 to45 min 4 80 20 100 0+0+8 Elective Demonstration Total 20 400 100 500 32 1 M.A. IInd SEMESTER Course Subject Papers Papers Code Time Credits External Internal Total L+T+P Category Marks M.A. Sitar Core-1 General and Applied MMU421 3 hours 4 80 20 100 4+0+0 Music Theory Core-2 History of Indian MMU422 3 hours 4 80 20 100 4+0+0 music Core-3 Stage performance MMUS423 35 to 45 4 80 20 100 0+0+8 min Core-4 Viva –Voce & MMUS424 35 to 45 4 80 20 100 0+0+8 Comparative Study min of Raga Core Lecture MMUS425 35 to45 4 80 20 100 0+0+8 Elective Demonstration min Open Open elective OE 426 3 hours 2 40 10 50 2+0+0 Elective Total 22 440 110 550 34 2 M.A.IIIrd SEMESTER. -

Sangit-Bhavana, Visva Bharati Department of Hindusthani Classical Music
Sangit-Bhavana, Visva Bharati Department of Hindusthani Classical Music CURRICULUM FOR UNDERGRADUATE COURSE CHOICE BASED CREDIT SYSTEM S.No. COURSE SEMESTER CREDITS MARKS FULL MARKS Core Course 1 14 Courses I –VI 14X6=84 14X75 1050 08 Courses Practical 06 Courses Theoretical Discipline Specific Elective Course (DSE) 2 04 Courses V- VI 4X6=24 4X75 300 03Courses Practical 01 course Theoretical Generic Elective Course (GEC) 04 Courses I-IV 4X6=24 4X75 300 3 03 Courses Practical 01 Course Theoretical Skill Enhancement Compulsory Course (SECC) 4 III-IV 2X2=4 2X25 50 02 Courses Theoretical Ability Enhancement I-II 2X2=4 2X25 50 Compulsory Course (AECC) 5 02 Courses Theoretical 6 Foundation Course I-II 2X4=8 2X50 100 (Tagore Studies) 02 Courses Theoretical Total: 26+2=28 Courses - - - 1850 1 CHOICE BASED CREDIT SYSTEM B.MUS (HONS) IN HINDUSTHANI CLASSICAL MUSIC (VOCAL) COURSE AND MARKS DISTRIBUTION STRUCTURE Core course AECC SECC DSE GEC TS SEM Total Prac Theo Prac Theo Prac Theo Prac Theo Prac Theo Theo I 75 75 - 25 - - - - 75 - 50 300 II 75 75 - 25 - - - - 75 - 50 300 III 150 75 - - - 25 - - 75 - - 325 IV 150 75 - - - 25 - - - 75 - 325 V 75 75 - - - - 150 - - - - 300 VI 75 75 - - - - 75 75 - - - 300 Total 600 450 - 50 - 50 225 75 225 75 100 1850 2 Sangit-Bhavana, Visva Bharati Department of Hindusthani Classical Music CURRICULUM FOR UNDERGRADUATE COURSE CHOICE BASED CREDIT SYSTEM B.MUS (HONS) IN HINDUSTHANI CLASSICAL MUSIC TABLE OF CONTENTS HINDUSTHANI CLASSICAL MUSIC (VOCAL) 4 HINDUSTHANI CLASSICAL MUSIC INSTRUMENTAL (SITAR) 21 HINDUSTHANI -

Vocal Grade 2 Introduction
Vocal Grade 2 Introduction Welcome to Vocal Grade 2 Hope you are enjoying this wonderful journey of music, having learnt quite a bit in the first level about the different types of Swars, Varnas, Alankars , Saptaks, and a lot many other singing techniques and melodious songs! Taking this journey forward into the next level, let us dive deep into learning few more concepts of singing and many more songs!! WHAT WILL YOU LEARN ? Grade 2 covers the following topics : • Introduction to Thaat . Characteristics / Rules of Thaat. Names of the ten Thaats and its swars. • Introduction to Raag. Characteristics / Rules of Raag. Comparison between Thaat and Raag. • Geet and its types • Raag Bhoopali • Raag Yaman • Laya • Alankars • Teen Taal and Rupak Taal • Brief note on the Harmonium • Concepts of Dhwani, Naad, Shruti, Vivadi Swar, Nyas Swar, Alap, Anuvadi Swar. • Properties of Naad • Many new songs • Harmonium / Synthesizer • Electronic Tabla / Tabla App How to Practice At Home Apart from the Booklet for grade 2, there will be video clippings shown for each topic in all the lessons. During practise at home, please follow the method shown in the Videos. Practice each lesson several times before meeting for the next lesson. A daily practice regime of a minimum of 30 minutes will suffice. Practising with the harmonium and the digital Tabla will certainly have an added advantage. Digital Tabla machines and Tabla software / apps are easily available and ideally should be used for daily practise. LESSON 1 In this lesson you will be learning about: • The Introduction to Thaat • Characteristics/Rules of Thaat • Names of Ten Thaats and its swars Concepts Introduction to Thaat Definition – Thaat is a concept which was developed to organise and classify the different ragas. -

Department of Music Online Class Plan from 30.3.2020 to 4.4.2020 Dr
Department of Music Online Class Plan from 30.3.2020 to 4.4.2020 Dr.Gurinder H.Singh Name of the course: (CBCS) BA Prog. Part 1, Sem 2, Hindustani Music Name of paper: Basics of Indian Musicology. (62444201) Name of unit: 1 and 2 Primary study material: Practical -Raga Jaunpuri - Reference Book, Pt. Bhatkhande, Kramik Pustak Mallika, Vol-4, starting from Pg. 604 a) Parichey b) Aroha, Avaroha, Pakad. Ability to sing and play on the Harmonium. b)Writing of the Notation in the Bandish in chota khayal (Theory) c) Learning to sing the Sthai d) Learning to sing the Antara. e) learning to sing 2 alaaps i ) Mandra to Madhya Saptak ii) Madhya Saptak to Taar Saptak. iii) learning to sing 3 Taans in 8 beats iv) learning to sing one Taan in 12 beats v) learning to sing one Taan in 16 beats. Raag Jaunpuri You Tube Links:- https://youtu.be/9FNv8CZAuA4 https://youtu.be/Ruqu6DPL6PI https://youtu.be/RPPMHvXciNA Dr. Gurinder H. Singh 7.4.2020 to 11.4.2020 Raga Kafi - Reference Book, Pt. Bhatkhande, Kramik Pustak Mallika. a) Parichey b) Aroha, Avaroha, Pakad. Ability to sing and play on the Harmonium. b)Writing of the Notation in the Bandish in chota khayal (Theory) c) Learning to sing the Sthai e) learning to sing 2 alaaps i ) Mandra to Madhya Saptak ii) Madhya Saptak to Taar Saptak. iii) learning to sing 3 Taans in 8 beats Theory Learning the Biographies of the following musicians. 1)Jaidev 2)Pt. Bhatkhande YouTube links. https://youtu.be/TLwO-2E9HGo Dr. -

Ustad Amir Khan, S
THE RECORD NEWS ============================================================= The journal of the ‘Society of Indian Record Collectors’, Mumbai ------------------------------------------------------------------------ ISSN 0971-7942 Volume - Annual: TRN 2006 ------------------------------------------------------------------------------------------------------------ S.I.R.C. Branches: Mumbai, Pune, Solapur, Nanded, Tuljapur, Baroda, Amravati ============================================================= Feature Article in this Issue: Gramophone Celebrities Master Ashraf Khan Gauhar Jan of Calcutta (C.1870-1930) Keshavrao Bhosle & Bal Gandharva Other articles: Ustad Amir Khan, S. D. Burman, Smt. Saraswati Rane 1 ‘The Record News’ - Annual magazine of ‘Society of Indian Record Collectors’ [SIRC] {Established: 1990} -------------------------------------------------------------------------------------------- President Narayan Mulani Hon. Secretary Suresh Chandvankar Hon. Treasurer Krishnaraj Merchant ==================================================== Patron Member: Mr. Michael S. Kinnear, Australia -------------------------------------------------------------------------------------------- Honorary Members V. A. K. Ranga Rao, Chennai Harmandir Singh Hamraz, Kanpur -------------------------------------------------------------------------------------------- Membership Fee: [Inclusive of the journal subscription] Annual Membership Rs. 1000 Overseas US $ 100 Life Membership Rs. 10000 Overseas US $ 1000 Annual term: July to June Members joining -

Scheme of Examinations and Syllabus of M.A
Kurukshetra University, Kurukshetra M. A. Music Credits According to CBCS in the Course Structure w.e.f 2016-17 1 credit =25 marks , the value of L+T+P is = 1+1+2 1 lecture = 1 credit, 1 Tutorial = 1 Credit, 2 Practical = 1 Credit M.A. Ist SEMESTER (Vocal) Course Subject Papers papers Code Time Credits External Internal Total (Hours/Week) Category Marks L+T+P M.A. Vocal Core-1 General and MMU 411 3 hours 4 80 20 100 4+0+0 Applied Music Theory Core-2 History of Indian MMU 412 3 hours 4 80 20 100 4+0+0 music Core-3 Stage performance MMUV413 35 to 45 min 4 80 20 100 0+0+8 Core-4 Viva –Voce & MMUV414 35 to 45 min 4 80 20 100 0+0+8 Comparative Study of Raga Core-5 Lecture MMUV415 35 to45 min 4 80 20 100 0+0+8 Elective Demonstration Total 20 400 100 500 32 1 M.A. IInd SEMESTER Course Subject Papers Papers Code Time Credits External Internal Total L+T+P Category Marks M.A. Vocal Core-1 General and Applied MMU421 3 hours 4 80 20 100 4+0+0 Music Theory Core-2 History of Indian MMU422 3 hours 4 80 20 100 4+0+0 music Core-3 Stage performance MMUV423 35 to 45 4 80 20 100 0+0+8 min Core-4 Viva –Voce & MMUV424 35 to 45 4 80 20 100 0+0+8 Comparative Study min of Raga Core Lecture MMUV425 35 to45 4 80 20 100 0+0+8 Elective Demonstration min Open General History and OE426 3 hours 2 40 10 50 2+0+0 Elective Basics of Indian Music (Inter-Disciplinary)* Total 22 440 110 550 34 2 M.A.IIIrd SEMESTER Course Subject Papers Papers Code Time Credits External Internal Total L+T+P Category Marks M.A. -

Sridhar Parsekar - in Memoriam
Sridhar Parsekar - In Memoriam Sridhar Parsekar (1920-1964) of Goa was the finest Hindustani violinist of the 20th century. He was a musician and a composer of the highest class. But his life was one of tragedy wrought by a wanton love of alcohol. That dissolute habit exacted from him a heavy price, drawing and quartering with withering efficiency every ounce of his mind, body and spirit (pardon the pun). Sridhar Parsekar perished in the late 1960s at the age of 44. Awhile back I requested Ravi Shankar to share some memories of Sridhar-bab. He sent this reply: "I knew Sridhar. He was a wonderful violinist, a disciple of Gajananrao Joshi. Sridhar Parsekar was a staff artist at AIR Bombay when Alla Rakha was also a staff member there. This is the period I knew him in the early forties. He was a smart young fellow, dark and very good looking. He came to hear me a lot and I also heard him a lot. I played one duet with him as I did with his Guru in the late 40's in Bombay. It was a wonderful duet I played with him and Alla Rakha accompanied us. Along with many other musicians Kishen Maharaj was sitting in the front. I admired him as a musician and I have always felt very sad how he ruined his life and killed himself with his addiction to alcohol." In 1993, the violinist V.G. Jog sent a message to the Usenet newsgroup rec.music.indian.classical (RMIC) in response to my query regarding Parsekar: "Sridhar Parsekar was a tayyar and sweet violinist. -

Bridging Chasms in Hindustani Music Retrieval
Bridging Chasms in Hindustani Music Retrieval A thesis submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy by Joe Cheri Ross (Roll No. 114050001) Under the guidance of Prof. Preeti Rao and Prof. Pushpak Bhattacharyya Department of Computer Science & Engineering, INDIAN INSTITUTE OF TECHNOLOGY BOMBAY December 2017 Declaration I declare that this written submission represents my ideas in my own words and where others ideas or words have been included I have adequately cited and referenced the original sources. I also declare that I have adhered to all principles of academic honesty and integrity and have not misrepresented or fabricated or falsified any idea/data/fact/source in my submission. I un- derstand that any violation of the above will be cause for disciplinary action by the Institute and can also evoke penal action from the sources which have thus not been properly cited or from whom proper permission has not been taken when needed. Joe Cheri Ross (Roll No: 114050001) Date: 22nd December 2017 Abstract Development of a music recommender system, one of the key applications of Music Informa- tion Retrieval (MIR), necessitates research into methods to represent and retrieve music infor- mation efficiently. Considering the specific characteristics of each music culture and the diverse requirements thereof, the methods must be culture-aware with many of the associated tasks be- ing culture-specific. This research is motivated by the importance of a music recommendation system for Hindustani music. The investigated tasks focus primarily on information extraction from melodic audio and text content, realizing the significance of information from multi-modal sources.