DOCSLIB.ORG

Statistical Properties of the Returns of Stock Prices of International Markets

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Statistical Properties of the Returns of Stock Prices of International Markets Statistical Properties of the Returns of Stock Prices of International Markets GabJin Oh∗ and Seunghwan Kim† Asia Pacific Center for Theoretical Physics, National Core Research Center for Systems Bio-Dynamics and Department of Physics, Pohang University of Science and Technology, Pohang, Gyeongbuk 790-784 Cheol-Jun Um‡ Department of Healthcare Management, Catholic University of Pusan, Busan 609-757 (Received 16 September 2005) We investigate statistical properties of daily international market indices of seven countries, and high-frequency S&P 500 and KOSDAQ data, by using the detrended fluctuation method and the surrogate test. We have found that the returns of international stock market indices of seven countries follow a universal power-law distribution with an exponent of ζ ≈ 3, while the Korean stock market follows an exponential distribution with an exponent of β ≈ 0.7. The Hurst exponent analysis of the original return, and its magnitude and sign series, reveal that the long-term-memory property, which is absent in the returns and sign series, exists in the magnitude time series with 0.7 ≤ H ≤ 0.8. The surrogate test shows that the magnitude time series reflects the non-linearity of the return series, which helps to reveal that the KOSDAQ index, one of the emerging markets, shows higher volatility than a mature market such as the S&P 500 index. PACS numbers: 02.50.-r, 89.90.+n, 05.40.-a, 05.45.TP. Keywords: Scaling, Long-term-Memory, Non-linearity, Volatility, DFA I. INTRODUCTION KOSDAQ 1-minute index from 1997 to 2004, to investi- gate diverse time characteristics of financial market in- dices. Up to now, numerous studies analyzing financial time series have been carried out to understand the complex economic systems made up of diverse and complicated We found that the returns of international stock mar- agents [1]. The statistical analysis of economic or fi- ket indices of seven countries follow a universal power-law nancial time series exhibits features different from the distribution with an exponent of ζ ≈ 3, while the Korean random-walk model based on the efficient market hy- stock market follows an exponential distribution with an pothesis (EMH), which are called stylized facts [2-15]. exponent of β ≈ 0.7. For a more detailed statistical anal- Previous studies showed that the returns of both stocks ysis, the original return time series is divided into mag- and foreign exchange rate have a variety of stylized facts. nitude and sign time series, and the corresponding Hurst For example, the distribution of financial time series fol- exponents are computed. The Hurst exponent analysis lows a universal power-law distribution with an exponent of the original return, and its magnitude and sign time ζ ≈ 3 [3-7]. While the temporal correlation of returns fol- series, reveal that the long-term-memory property, which lows the process of random walks, the volatility of returns is absent in the return and sign time series, exists in the shows a long-term-memory property [12-15]. However, magnitude time series with 0.7 ≤ H ≤ 0.8. recent work has revealed that the distribution function of returns in emerging markets follows an exponential dis- tribution, while the mature markets follow a power-law In order to test the nonlinearity of the time series, the distribution with an exponent ζ ≈ 3 [11]. surrogate test is performed for all time series. We find In this paper, we use Detrended Fluctuation Analysis that the magnitude time series reflects the non-linearity (DFA), which was introduced by Peng et al. to find the of the return series, which helps to reveal that the KOS- long-term-memory property of time series data [16] and DAQ index, one of the emerging markets, shows higher arXiv:physics/0601126v1 [physics.data-an] 18 Jan 2006 utilizes the surrogate test method proposed by Theiler et volatility than a mature market such as the S&P 500 al. to measure the non-linearity of time series [17]. We index. study daily international market indices of seven coun- tries from 1991 to 2005, the high-frequency S&P 500 5- minute index from 1995 to 2004, and the high-frequency In the next section, we explain the market data used in our investigations. In Section III., we introduce the methods of the surrogate test and detrended fluctuation analysis (DFA). In Section IV., the results of the statis- ∗Electronic address: [email protected] tical analysis for various time series of the market data †Electronic address: [email protected] are presented. Finally, we end with a summary of our ‡Electronic address: [email protected] findings. 2 II. DATA Then, rk is multiplied by random phases, We use the return series in eight daily international iφk market indices of seven countries from 1991 to 2005, the r˜k = rke , (4) S&P 500 index (5 minutes) from 1995 to 2004, and the φ π KOSDAQ index (1 minute) from 1997 to 2004. The seven where k is uniformly distributed in [0, 2 ]. The inverse r countries are France (CAC40), Germany (DAX), United FFT of ˜k gives the surrogate data retaining the linearity Kingdom (FTSE100), Hong Kong (HangSeng), KOREA in the original time series, (KOSPI), America (NASDAQ), Japan (Nikkei225), and America (S&P 500). We make use of the normalized N ′ 1 return often used in the financial time series analysis in- r = r˜ e−i2πnk/N . (5) n N X k stead of the stock prices. Let y1,y2, ....yn, be the daily k=1 stock prices. The normalized return Rt at a given time t is defined by In the third step, non-linear measurements with the en- tropy, the dimension, and Lyapunov exponents are per- formed for the original data and the surrogate data, re- r y y , t = ln t+1 − ln t spectively. Finally, the difference in measurements of the ln yt+1 − ln yt original data and the surrogate data is tested for signifi- Rt ≡ , (1) σ(rt) cance. If significant, the hypothesis will be rejected and the original data are regarded as having non-linearity. where σ(rt) is the standard deviation of the return. The normalized returns Rt are divided into magnitude and sign series by using the following relation: B. Detrended Fluctuation Analysis R R Sign , k,t = | k,t|× k,t (2) The typical methods to analyze the long-term-memory where Rk,t is the return series of the k-th market index property in the time series data are largely classified into calculated by the log-difference, |Rk,t| the magnitude se- three types: the re-scaled range analysis (R/S) method ries of the returns of the k-th market index, and Signk,t proposed by Mandelbrot and Wallis [19], the modified the sign series with +1 for the upturn and −1 for the R/S analysis by Lo et al. [18], and the DFA (detrended et al. downturn. Note that the magnitude series |Rt| from tak- fluctuation analysis) method by Peng [20]. In this ing the absolute value of the return measures the size of paper, the DFA method is used due to its effectiveness the return change, and the sign series Signt measures the even for the absence of long-term memory. The Hurst direction of the change. The volatility of the returns can exponent can be calculated by the DFA method through be studied though the magnitude series |Rt|. the following process. Step (1): The time series after the subtraction of the mean are accumulated as follows: III. METHODS N A. Surrogate Test y(i)= [x(i) − x¯], (6) X i=1 The surrogate test method was first proposed by Theiler et al. to prove the non-linearity contained in where x(i) are the i-th time series, andx ¯ is the mean of the time series [17]. The surrogate data test can be ex- the whole time series. This accumulation process is one plained by the following four steps [16]. First, a null that changes the original data into a self-similar process. hypothesis is made and the features of the linear pro- Step (2): The accumulated time series are divided into cess following the hypothesis are defined. In general, the boxes of the same length n. In each box of length n, linearity uses the mean, the variance, and the autocorre- the trend is estimated through the ordinary least square lation of the original time series. The surrogate data are method, called DFA(m), where m is the order of fitting. randomly generated but retain the autocorrelation func- In each box, the ordinary least square line is expressed as tion, the mean, and the variance of the original data. In yn(i). By subtracting yn(i) from the accumulated y(i) in the second step, the surrogate data are created through each box, the trend is removed. This process is applied the Fast Fourier Transform(FFT) method. Let rn be the to every box and the fluctuation magnitude is calculated original time series. The Fourier Transform rk of rn is by using given by N 1 N 1 i2πnk/N v 2 r = r e . (3) F (n)= u [y(i) − yn(k)] . (7) k N X n uN X n=1 t i=1 3 (a) 1.1 CAC40 r e t u r n s DAX m a g n i t u d e −1 FTSE100 HangSeng 1 s i g n NASDAQ r e t u r n s ( s u r r o ) Nikkei225 m a g n i t u d e ( s u r r o ) S&P500 s i g n ( s u r r o ) Power Law(3.3) 0.9 −1.5 3.3 CDF 0.8 −2 0.7 0.6 −2.5 0.5 log R 10 0.5 (b) Exponential ( 0.7 ) kospi 0.4 −1 1 2 3 4 5 6 7 8 Country −2 0.7 −3 FIG.
Load more

Recommended publications
  • Download Download
    The Journal of Applied Business Research – September/October 2017 Volume 33, Number 5 The Effect Of Corporate Governance On Unfaithful Disclosure Designation And Unfaithful Disclosure Penalty Points Bo Young Moon, Dankook University, South Korea Soo Yeon Park, Korea University, South Korea ABSTRACT This paper investigates the relation between Unfaithful Disclosure Corporations (“UDC”) and corporate governance using listed firm (KOSPI and KOSDAQ) data in Korea. Prior literature reports that corporate governance has an impact on the level of disclosure and the quality of disclosure provided by companies. However, it is hard to find the studies about corporate governance and UDC at the term of disclosure quality. Compare to some financially advanced countries, Korea established corporate governance in a relatively short period of time; hence concerns have been raised the corporate governance have not played effective role to monitor management. We question how corporate governance affects companies’ unfaithful disclosure by using several corporate governance proxy variables and UDC data which is unique system in Korea. From the empirical tests, we find a negative association between the proportion of outside directors, an indicator of the board’s independence, and UDC designation, among companies listed on both KOSPI and KOSDAQ. On the other hand, there is a significant positive association between the proportion of outside directors and UDCs’ imposed and accumulated penalty points among KOSDAQ-listed companies. This implies that outside director system effectively play a monitoring role however due to different natures of members included in outside directors, the system often fails to control regarding based reasons for penalty points imposition. In addition, we find the percentage of foreign equity ownership showed statistically significant positive association with UDC designation and a significant positive association with the imposed and accumulated penalty points among KOSPI-listed companies.
    [Show full text]
  • Does the Market React Differently to Chaebol Firms?
    The Journal of Applied Business Research – September/October 2014 Volume 30, Number 5 Does The Market React Differently To Chaebol Firms? Heejin Park, Hanyang University, South Korea Jinsoo Kim, Hanyang University, South Korea Mihye Ha, Hanyang University, South Korea Sambock Park, Hanyang University, South Korea ABSTRACT Based on a sample of Korean firms listed on the KOSPI and KOSDAQ from 2001 to 2011, we examined whether the affiliation of a firm with a Chaebol group affects the sensitivity of stock prices to earnings surprises. We found that the market response to positive (negative) earnings surprises is more positive (negative) for Chaebol firms than for non-Chaebol firms. In addition, we investigated how intra-group transactions affect the ERCs of Chaebol firms by comparing with those of non-Chaebol firms. Our results show that the intra-group transactions of Chaebol firms are positively related to ERCs under both positive and negative earnings surprises. However, we did not find the same results from the analyses of non-Chaebol firms. Keywords: Chaebol Firms; Earnings Response Coefficient (ERC); Earnings Surprises; KOSPI; KOSDAQ 1. INTRODUCTION he aim of this study is to examine how differently the market reacts to earnings surprises of Chaebol firms compared to those of non-Chaebol firms. Although there is no official definition of Chaebol, T firms are perceived as Chaebol if they consist of a large group and operate in many different industries, maintain substantial business ties with other firms in their group, and are controlled by the largest shareholder as a whole. The definition used to identify Chaebol firms is that of a large business group established by the Korea Fair Trade Commission (KFTC) and a group of companies of which more than 30% of the shares are owned by the group’s controlling shareholders and its affiliated companies.
    [Show full text]
  • For Additional Information
    April 2015 Attached please find the updated Foreign Listed Stock Index Futures and Options Approvals Chart, current as of April 2015. All prior versions are superseded and should be discarded. Please note the following developments since we last distributed the Approvals Chart: (1) The CFTC has approved the following contracts for trading by U.S. Persons: (i) Singapore Exchange Derivatives Trading Limited’s futures contract based on the MSCI Malaysia Index; (ii) Osaka Exchange’s futures contract based on the JPX-Nikkei Index 400; (iii) ICE Futures Europe’s futures contract based on the MSCI World Index; (iv) Eurex’s futures contracts based on the Euro STOXX 50 Variance Index, MSCI Frontier Index and TA-25 Index; (v) Mexican Derivatives Exchange’s mini futures contract based on the IPC Index; (vi) Australian Securities Exchange’s futures contract based on the S&P/ASX VIX Index; and (vii) Moscow Exchange’s futures contract based on the MICEX Index. (2) The SEC has not approved any new foreign equity index options since we last distributed the Approvals Chart. However, the London Stock Exchange has claimed relief under the LIFFE A&M and Class Relief SEC No-Action Letter (Jul. 1, 2013) to offer Eligible Options to Eligible U.S. Institutions. See note 16. For Additional Information The information on the attached Approvals Chart is subject to change at any time. If you have questions or would like confirmation of the status of a specific contract, please contact: James D. Van De Graaff +1.312.902.5227 [email protected] Kenneth M.
    [Show full text]
  • Mr. Alp Eroglu International Organization of Securities Commissions (IOSCO) Calle Oquendo 12 28006 Madrid Spain
    1301 Second Avenue tel 206-505-7877 www.russell.com Seattle, WA 98101 fax 206-505-3495 toll-free 800-426-7969 Mr. Alp Eroglu International Organization of Securities Commissions (IOSCO) Calle Oquendo 12 28006 Madrid Spain RE: IOSCO FINANCIAL BENCHMARKS CONSULTATION REPORT Dear Mr. Eroglu: Frank Russell Company (d/b/a “Russell Investments” or “Russell”) fully supports IOSCO’s principles and goals outlined in the Financial Benchmarks Consultation Report (the “Report”), although Russell respectfully suggests several alternative approaches in its response below that Russell believes will better achieve those goals, strengthen markets and protect investors without unduly burdening index providers. Russell is continuously raising the industry standard for index construction and methodology. The Report’s goals accord with Russell’s bedrock principles: • Index providers’ design standards must be objective and sound; • Indices must provide a faithful and unbiased barometer of the market they represent; • Index methodologies should be transparent and readily available free of charge; • Index providers’ operations should be governed by an appropriate governance structure; and • Index providers’ internal controls should promote efficient and sound index operations. These are all principles deeply ingrained in Russell’s heritage, practiced daily and they guide Russell as the premier provider of indices and multi-asset solutions. Russell is a leader in constructing and maintaining securities indices and is the publisher of the Russell Indexes. Russell operates through subsidiaries worldwide and is a subsidiary of The Northwestern Mutual Life Insurance Company. The Russell Indexes are constructed to provide a comprehensive and unbiased barometer of the market segment they represent. All of the Russell Indexes are reconstituted periodically, but not less frequently than annually or more frequently than monthly, to ensure new and growing equities and fixed income securities are reflected in its indices.
    [Show full text]
  • Thomson One Quick Reference Guide
    THOMSON ONE QUICK REFERENCE GUIDE Thomson ONE (www.thomsonone.com) provides integrated access to comprehensive market and company information. All of the intelligence you need to power your knowledge gathering and drive smarter decision-making. This Quick Reference Card offers some quick tips on customizing your workspace, setting up alerts, searching and more. LOOKING UP A COMPANY To add a service to your Favorites, open the page, click , and then select Add to Favorites. PUBLIC COMPANIES: To organize your favorites 1. If the company symbol is not known, click the 1. Click , and select Organize Favorites. Search icon. 2. If you want to create and name folders, click 2. Select either Contains or Begins With, then type all or Create Folder, and type in a name. part of the company name. 3. Drag a favorite into any folder, or click up or down 3. (Optional) Click the Home Listing Only check box to arrows to move it to a different place in the list. limit results to a company’s primary (Home) exchange. 4. Click OK. 4. Click Search. 5. Select the company symbol to display content related To set any page as your Home Page to that company. Click , and select Set as Home. PRIVATE COMPANIES: To return to your home page at any time, click . 1. Click the Symbol drop-down, and select Private Co. FLEX MONITOR: MONITORING A 2. Type the private company name (use , if needed), and click Go. COVERAGE LIST 3. Select the private company name to display content Flex Monitor allows you to create and save an unlimited related to that company.
    [Show full text]
  • List of Approved Regulated Stock Exchanges
    Index Governance LIST OF APPROVED REGULATED STOCK EXCHANGES The following announcement applies to all equity indices calculated and owned by Solactive AG (“Solactive”). With respect to the term “regulated stock exchange” as widely used throughout the guidelines of our Indices, Solactive has decided to apply following definition: A Regulated Stock Exchange must – to be approved by Solactive for the purpose calculation of its indices - fulfil a set of criteria to enable foreign investors to trade listed shares without undue restrictions. Solactive will regularly review and update a list of eligible Regulated Stock Exchanges which at least 1) are Regulated Markets comparable to the definition in Art. 4(1) 21 of Directive 2014/65/EU, except Title III thereof; and 2) provide for an investor registration procedure, if any, not unduly restricting foreign investors. Other factors taken into account are the limits on foreign ownership, if any, imposed by the jurisdiction in which the Regulated Stock Exchange is located and other factors related to market accessibility and investability. Using above definition, Solactive has evaluated the global stock exchanges and decided to include the following in its List of Approved Regulated Stock Exchanges. This List will henceforth be used for calculating all of Solactive’s equity indices and will be reviewed and updated, if necessary, at least annually. List of Approved Regulated Stock Exchanges (February 2017): Argentina Bosnia and Herzegovina Bolsa de Comercio de Buenos Aires Banja Luka Stock Exchange
    [Show full text]
  • FTSE Global Equity Index Series Ground Rules Visit Or E-Mail [email protected]
    Ground Rules FTSE Global Equity Index Series v10.9 ftserussell.com An LSEG Business September 2021 Contents 1.0 Introduction .................................................................... 3 2.0 Management Responsibilities ....................................... 5 3.0 FTSE Russell Index Policies ......................................... 7 4.0 Country Inclusion Criteria ............................................. 9 5.0 Inclusion Criteria .......................................................... 11 6.0 Eligible Security Screens ............................................ 12 7.0 Periodic Review of Constituents ................................ 16 8.0 Additions Outside of a Review ................................... 21 9.0 Corporate Actions and Events .................................... 24 10.0 Treatment of Dividends ............................................... 26 11.0 Industry Classification Benchmark (ICB)................... 27 12.0 Algorithm and Calculation Method ............................. 28 Appendix A: Eligible Exchanges and Market Segments .... 29 Appendix B: Eligible Classes of Securities ......................... 34 Appendix C: Calculation Schedule ...................................... 39 Appendix D: Country Additions and Deletions ................... 41 Appendix E: Country Classification ..................................... 43 Appendix F: Country Indices ................................................ 44 Appendix G: FTSE Russell China Share Descriptions ....... 45 Appendix H: Further Information ........................................
    [Show full text]
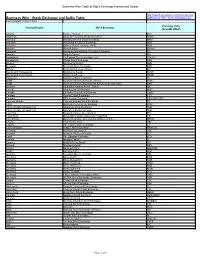
  • Stock Exchange and Suffix Table Ml/Business Wire Stock Exchanges.Pdf Last Updated 12 March 2021
    Business Wire Table of Stock Exchange Names and Usage http://www.businesswire.com/schema/news Business Wire - Stock Exchange and Suffix Table ml/Business_Wire_Stock_Exchanges.pdf Last Updated 12 March 2021 Exchange Value Country/Region Stock Exchange (NewsML ONLY) Albania Bursa e Tiranës BET Argentina Bolsa de Comercio de Buenos Aires BCBA Armenia Nasdaq Armenia Stock Exchange ARM Australia Australian Securities Exchange ASX Australia Sydney Stock Exchange (APX) APX Austria Wiener Börse WBAG Bahamas Bahamas International Securities Exchange BS Bahrain Bahrain Bourse BH Bangladesh Chittagong Stock Exchange, Ltd. CSEBD Bangladesh Dhaka Stock Exchange DSE Belgium Euronext Brussels BSE Bermuda Bermuda Stock Exchange BSX Bolivia Bolsa Boliviana de Valores BO Bosnia and Herzegovina Banjalucka Berza BLSE Bosnia and Herzegovina Sarajevska Berza SASE Botswana Botswana Stock Exchange BT Brazil Bolsa de Valores do Rio de Janeiro BVRJ Brazil Bolsa de Valores, Mercadorias & Futuros de Sao Paulo SAO Bulgaria Balgarska fondova borsa - Sofiya BB Canada Aequitas NEO Exchange NEO Canada Canadian Securities Exchange CNSX Canada Toronto Stock Exchange TSX Canada TSX Venture Exchange TSX VENTURE Cayman Islands Cayman Islands Stock Exchange KY Chile Bolsa de Comercio de Santiago SGO China, People's Republic of Shanghai Stock Exchange SHH China, People's Republic of Shenzhen Stock Exchange SHZ Colombia Bolsa de Valores de Colombia BVC Costa Rica Bolsa Nacional de Valores de Costa Rica CR Cote d'Ivoire Bourse Regionale Des Valeurs Mobilieres S.A. BRVM Croatia
    [Show full text]
  • List of Asian Stock Exchanges
    List of Asian stock exchanges This is a list of Asian stock exchanges. In the Asian region, there are multiple stock exchanges. As per data from World Federation of Exchanges, below are top 10 selected in 2019:[1][2] Tokyo Stock Exchange, Japan Shanghai Stock Exchange, China Hong Kong Stock Exchange, Hong Kong Shenzhen Stock Exchange, China Bombay Stock Exchange, India National Stock Exchange, India Korea Exchange, South Korea Taiwan Exchange, Taiwan Singapore Exchange, Singapore The Stock Exchange of Thailand, Thailand Asia Contents Stock exchanges Central Asian East Asian North Asia South Asian Southeast Asian West Asian See also References External links Stock exchanges Central Asian Operating Economy Exchange Location Founded Listings Link Technology MIC KASE (http Kazakhstan Stock Almaty 1993 127 s://kase.k Exchange z/en/) Kazakhstan Astana AIX (http Nasdaq Nur- International 2018 25 s://www.ai Matching AIXK Sultan Exchange x.kz/) Engine[3] KSE (htt Kyrgyz Stock Bishkek 1994 p://www.ks Kyrgyzstan Exchange (KSE) e.kg/) CASE (http Central Asian s://www.ca Dushanbe 2015 Tajikistan Stock Exchange se.com.tj/e n/) SRCMET State Commodity (https://ww and Raw Material Ashgabat 1994 w.exchang Exchange of Turkmenistan e.gov.tm/?l Turkmenistan ang=en) UZSE (http Tashkent Stock Tashkent 1994 104 s://uzse.u Uzbekistan Exchange z/) East Asian Economy Exchange Location Founded Listings Link Shanghai Stock SSE (http://www.sse.com. Shanghai 1990 Exchange cn) Shenzhen Stock SZSE (http://www.szse.cn/ Shenzhen 1991 2,375 (Jan 2021) Mainland Exchange main/) China Dalian Commodity DCE (http://www.dce.com. Dalian 1993 Exchange cn/DCE/) SEHK (https://web.archive.
    [Show full text]
  • Information Transmission Between NASDAQ and Asian Secondary
    Information Transmission between NASDAQ and Asian Second Board Markets Bong-Soo Lee∗, Oliver Meng Rui!, and Steven Shuye Wang! Abstract In Asia, NASDAQ's success has helped prompt Singapore (SESDAQ), Japan (JASDAQ), Taiwan (TAISDAQ) and South Korea (KOSDAQ) to set up or formalize their own second board markets in the 1980s and early 1990s. In 1999, Malaysia (MESDAQ) and Hong Kong (GEM) also set up their second board markets. Given the growing importance of these second board markets, we examine whether there is any evidence of spillovers from NASDAQ returns and volatilities to Asian second board market returns and volatilities and whether the cross-country spillovers are strong relative to domestic spillovers from the corresponding main board markets. For this purpose, we employ EGARCH models, dynamic causality tests, and VAR-based forecast error decompositions using daily data of a recent sample period that includes the Asian financial crisis of 1997 and up to April 20, 2001. We find that, first, there is strong evidence of lagged returns and volatility spillovers from the NASDAQ market to the Asian second board markets when we exclude contemporaneous main board market returns. Second, there is strong evidence of contemporaneous and lagged returns and volatility spillovers from the local main board markets to the corresponding second board markets. However, even in the presence of contemporaneous main board market returns, there remain substantial spillovers from the lagged NASDAQ returns and volatilities to Asian second board market returns and volatilities. These findings are not sensitive to whether we use U.S. dollar-based data or local currency-based data.
    [Show full text]
  • SBI Holdings, Inc. Financial Results for the Six-Month Period Ended Sept
    Strategic Business Innovator SBI Holdings, Inc. Financial Results for the Six-Month Period Ended Sept. 30, 2011 (Fiscal Year Ending March 31, 2012) October 26, 2011 The items in this document are provided as information related to the business strategy of the SBI Group companies and not as an invitation to invest in the stock or securities issued by each company. None of the Group companies guarantees the completeness of this document in terms of information and future business strategy. The content of this document is subject to revision or cancellation without warning. Note: Fiscal Year (“FY”) ends March 31 of the following year 1 1. Overall Summary of 1H FY2011 2. Measures to Realize Continuous Growth in Anticipation of a More Difficult Business Environment 2 1. Overall Summary of 1H FY2011 (1) The operating environment is ever more challenging due to the Great East Japan Earthquake, delay in the US economic recovery, European debt crisis and slowdown in emerging economies. But the SBI Group achieved a growth in ordinary and net income in the 1H of FY2011 (2) The Group promoted cost reduction and reorganization on a group-wide basis in anticipation of the worsening business environment 3 (1) The operating environment is ever more challenging due to the Great East Japan Earthquake, delay in the US economic recovery, European debt crisis and slowdown in emerging economies. But the SBI Group achieved a growth in ordinary and net income in the 1H of FY2011 4 Business Environment Worsening Owing to the Great East Japan Earthquake and the Continuance of the Debt Crisis of the Euro Zone Stock prices fell around the world, even in emerging countries Rates of decline from the highest prices since the Lehman Shock (Sept.
    [Show full text]
  • Comparative Analysis of Indian Stock Market with International Markets
    Comparative Analysis of Indian Stock Market with International Markets Debjiban Mukherjee T. A. Pai Management Institute, Manipal, India Abstract The stock market is witnessing heightened activities and is increasingly gaining importance. In the current context of globalization and the subsequent integration of the global markets this paper captures the trends, similarities and patterns in the activities and movements of the Indian Stock Market in comparison to its international counterparts. This study covers New York Stock Exchange (NYSE), Hong Kong Stock exchange (HSE), Tokyo Stock exchange (TSE), Russian Stock exchange (RSE), Korean Stock exchange (KSE) from various socio- politico-economic backgrounds. Both the Bombay Stock exchange (BSE) and the National Stock Exchange of Indian Limited (NSE) have been used in the study as a part of Indian Stock Market. The time period has been divided into various eras to test the correlation between the various exchanges to prove that the Indian markets have become more integrated with its global counterparts and its reaction are in tandem with that are seen globally. Keywords: Stock Market, Comparative Analysis, Statistical analysis, Efficiency Test. 39 ©Great Lakes Herald – April 2007 Volume 1, Issue 1 by Great Lakes Institute of Management, Chennai 1. Introduction The Indian stock exchanges hold a place of prominence not only in Asia but also at the global stage. The Bombay Stock Exchange (BSE) is one of the oldest exchanges across the world, while the National Stock Exchange (NSE) is among the best in terms of sophistication and advancement of technology. The Indian stock market scene really picked up after the opening up of the economy in the early nineties.
    [Show full text]