Spatial Variability of Levees As Measured Using the CPT
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Physical Geography of Southeast Asia
Physical Geography of Southeast Asia Creating an Annotated Sketch Map of Southeast Asia By Michelle Crane Teacher Consultant for the Texas Alliance for Geographic Education Texas Alliance for Geographic Education; http://www.geo.txstate.edu/tage/ September 2013 Guiding Question (5 min.) . What processes are responsible for the creation and distribution of the landforms and climates found in Southeast Asia? Texas Alliance for Geographic Education; http://www.geo.txstate.edu/tage/ September 2013 2 Draw a sketch map (10 min.) . This should be a general sketch . do not try to make your map exactly match the book. Just draw the outline of the region . do not add any features at this time. Use a regular pencil first, so you can erase. Once you are done, trace over it with a black colored pencil. Leave a 1” border around your page. Texas Alliance for Geographic Education; http://www.geo.txstate.edu/tage/ September 2013 3 Texas Alliance for Geographic Education; http://www.geo.txstate.edu/tage/ September 2013 4 Looking at your outline map, what two landforms do you see that seem to dominate this region? Predict how these two landforms would affect the people who live in this region? Texas Alliance for Geographic Education; http://www.geo.txstate.edu/tage/ September 2013 5 Peninsulas & Islands . Mainland SE Asia consists of . Insular SE Asia consists of two large peninsulas thousands of islands . Malay Peninsula . Label these islands in black: . Indochina Peninsula . Sumatra . Label these peninsulas in . Java brown . Sulawesi (Celebes) . Borneo (Kalimantan) . Luzon Texas Alliance for Geographic Education; http://www.geo.txstate.edu/tage/ September 2013 6 Draw a line on your map to indicate the division between insular and mainland SE Asia. -

Imaging Laurentide Ice Sheet Drainage Into the Deep Sea: Impact on Sediments and Bottom Water
Imaging Laurentide Ice Sheet Drainage into the Deep Sea: Impact on Sediments and Bottom Water Reinhard Hesse*, Ingo Klaucke, Department of Earth and Planetary Sciences, McGill University, Montreal, Quebec H3A 2A7, Canada William B. F. Ryan, Lamont-Doherty Earth Observatory of Columbia University, Palisades, NY 10964-8000 Margo B. Edwards, Hawaii Institute of Geophysics and Planetology, University of Hawaii, Honolulu, HI 96822 David J. W. Piper, Geological Survey of Canada—Atlantic, Bedford Institute of Oceanography, Dartmouth, Nova Scotia B2Y 4A2, Canada NAMOC Study Group† ABSTRACT the western Atlantic, some 5000 to 6000 State-of-the-art sidescan-sonar imagery provides a bird’s-eye view of the giant km from their source. submarine drainage system of the Northwest Atlantic Mid-Ocean Channel Drainage of the ice sheet involved (NAMOC) in the Labrador Sea and reveals the far-reaching effects of drainage of the repeated collapse of the ice dome over Pleistocene Laurentide Ice Sheet into the deep sea. Two large-scale depositional Hudson Bay, releasing vast numbers of ice- systems resulting from this drainage, one mud dominated and the other sand bergs from the Hudson Strait ice stream in dominated, are juxtaposed. The mud-dominated system is associated with the short time spans. The repeat interval was meandering NAMOC, whereas the sand-dominated one forms a giant submarine on the order of 104 yr. These dramatic ice- braid plain, which onlaps the eastern NAMOC levee. This dichotomy is the result of rafting events, named Heinrich events grain-size separation on an enormous scale, induced by ice-margin sifting off the (Broecker et al., 1992), occurred through- Hudson Strait outlet. -

LIESSE Où Klaxonner Pour Faire Chier P. 17 LA POSTE Schwaller De Rien P. 16 DÉCROISSANCE Un Art Consommé P. 7 FOOT Bilan Et P
Vendredi 22 juin 2018 // No 369 // 9e année CHF 4.– // Abonnement annuel CHF 160.– // www.vigousse.ch FOOT DÉCROISSANCE LA POSTE LIESSE Bilan et perspectives Un art consommé Schwaller Où klaxonner pour PP. 2, 3, 4, 14 P. 7 de rien P. 16 faire chier P. 17 JAA – 1001 Lausanne P.P./Journal – Poste CH SA – Poste Lausanne P.P./Journal JAA – 1001 2 C’EST PAS POUR DIRE ! POINT V 3 opposants se font mystérieusement empoisonner, un Etat qui inonde le Y a faute, ou bien ? reste du monde de fake news, de faits Parité bien alternatifs, de théories du complot et FOOT NEWS On nous cache tout, on nous dit rien ! La vérité est de désinformation stupide, une clique malmenée de partout, sauf, heureusement, dans le seul domaine qui truque toutes les élections depuis qui compte : le football. des années, bref, le royaume du faux ordonnée… et de la magouille. Mais pour le foot, faut pas déconner quand même : on Séverine André Ce lundi, tandis que les petits Suisses mais y a hors-jeu là ! » ; « Hé ! Quel peut parfaitement faire confiance à se remettaient à peine de la nuit de connard, il l’a poussé ! » ; ou « Quel ces mythos. Car le football, c’est la t soudain, dimanche 17 juin, après des folie faisant suite au glorieux match enculé, il s’est laissé tomber ! » Très vérité. nul contre le Brésil, les élèves fran- clairement, c’est le cas que p si, et siècles d’iniquité, la Suisse s’enthousiasme çais gambergeaient sec devant leur seulement si, il y a effectivement Autre preuve que la vérité, c’est pour l’égalité. -

Groundwater Issues in the Paleozoic Plateau a Taste of Karst, a Modicum of Geology, and a Whole Lot of Scenery
GGroundwaterroundwater IssuesIssues inin tthehe PaleozoicPaleozoic PlateauPlateau A Taste of Karst, a Modicum of Geology, and a Whole Lot of Scenery Iowa Groundwater Association Field Trip Guidebook No. 1 Iowa Geological and Water Survey Guidebook Series No. 27 Dunning Spring, near Decorah in Winneshiek County, Iowa September 29, 2008 In Conjunction with the 53rd Annual Midwest Ground Water Conference Grand River Center, Dubuque, Iowa, September 30 – October 2, 2008 Groundwater Issues in the Paleozoic Plateau A Taste of Karst, a Modicum of Geology, and a Whole Lot of Scenery Iowa Groundwater Association Field Trip Guidebook No. 1 Iowa Geological and Water Survey Guidebook Series No. 27 In Conjunction with the 53rd Annual Midwest Ground Water Conference Grand River Center, Dubuque, Iowa, September 30 – October 2, 2008 With contributions by M.K. Anderson Robert McKay Iowa DNR-Water Supply Engineering Iowa DNR-Geological and Water Survey Bruce Blair Jeff Myrom Iowa DNR-Forestry Iowa DNR-Solid Waste Michael Bounk Eric O’Brien Iowa DNR-Geological and Water Survey Iowa DNR-Geological and Water Survey Karen Osterkamp Lora Friest Iowa DNR-Fisheries Northeast Iowa Resource Conservation and Development Jean C. Prior Iowa DNR-Geological and Water Survey James Hedges Luther College James Ranum Natural Resources Conservation Service John Hogeman Winneshiek County Landfi ll Operator Robert Rowden Iowa DNR-Geological and Water Survey Claire Hruby Iowa DNR-Geographic Information Systems Joe Sanfi lippo Iowa DNR-Manchester Field Offi ce Bill Kalishek Gary Siegwarth Iowa DNR-Fisheries Iowa DNR-Fisheries George E. Knudson Mary Skopec Luther College Iowa DNR-Geological and Water Survey Bob Libra Stephanie Surine Iowa DNR-Geological and Water Survey Iowa DNR-Geological and Water Survey Huaibao Liu Paul VanDorpe Iowa DNR-Geological and Water Survey Iowa DNR-Geological and Water Survey Iowa Department of Natural Resources Richard Leopold, Director September 2008 CONTENTS INTRODUCTION . -

Part 629 – Glossary of Landform and Geologic Terms
Title 430 – National Soil Survey Handbook Part 629 – Glossary of Landform and Geologic Terms Subpart A – General Information 629.0 Definition and Purpose This glossary provides the NCSS soil survey program, soil scientists, and natural resource specialists with landform, geologic, and related terms and their definitions to— (1) Improve soil landscape description with a standard, single source landform and geologic glossary. (2) Enhance geomorphic content and clarity of soil map unit descriptions by use of accurate, defined terms. (3) Establish consistent geomorphic term usage in soil science and the National Cooperative Soil Survey (NCSS). (4) Provide standard geomorphic definitions for databases and soil survey technical publications. (5) Train soil scientists and related professionals in soils as landscape and geomorphic entities. 629.1 Responsibilities This glossary serves as the official NCSS reference for landform, geologic, and related terms. The staff of the National Soil Survey Center, located in Lincoln, NE, is responsible for maintaining and updating this glossary. Soil Science Division staff and NCSS participants are encouraged to propose additions and changes to the glossary for use in pedon descriptions, soil map unit descriptions, and soil survey publications. The Glossary of Geology (GG, 2005) serves as a major source for many glossary terms. The American Geologic Institute (AGI) granted the USDA Natural Resources Conservation Service (formerly the Soil Conservation Service) permission (in letters dated September 11, 1985, and September 22, 1993) to use existing definitions. Sources of, and modifications to, original definitions are explained immediately below. 629.2 Definitions A. Reference Codes Sources from which definitions were taken, whole or in part, are identified by a code (e.g., GG) following each definition. -

Documentation of Design Deficiencies Santa Clara River Levee System (Scr-1) 1
DOCUMENTATION OF DESIGN DEFICIENCIES SANTA CLARA RIVER LEVEE SYSTEM (SCR-1) 1. Project Description and Watershed Characteristics The Santa Clara River Levee (SCR-1) system is located in the city of Oxnard, in Ventura County, California. It is approximately 4.72 miles long, extending along the southeast bank of the Santa Clara River from Highway 101, at its downstream terminus, to the community of Saticoy, at its upstream terminus (see Figure 1). SCR-1 was originally designed in 1958 by the U.S. Army Corps of Engineers (Corps) to control the Corps’ predicted Standard Project Flood peak discharge of 225,000 cubic feet per second (cfs), a peak emanating from a partially regulated 1,600-square-mile Santa Clara River watershed. The height of SCR-1 varies from approximately 4 feet to 13 feet. The compacted fill embankment that forms SCR-1 has a top width of 18 feet. The levee embankment slopes are 2 horizontal to 1 vertical (2H:1V), on both the landward side and the riverward side. The riverward side of the embankment has a 1.5- to 2- foot-thick rock revetment, with a concrete facing at and near highway bridges. The rock revetment extends from the top of the embankment to varying depths. The lowest depth of the rock revetment is hereinafter referred to as the “toedown.” Construction of the SCR-1 project was completed in 1961. The levee was constructed adjacent to the active channel of the Santa Clara River. A review of historical aerial photography, dating as far back as 1927, indicates that before construction of the SCR-1, there were numerous locations along the project reach where the primary braid of the Santa Clara River impinged directly on the east and west banks of the river at rather abrupt flow angles. -

Hogback Is Ridge Formed by Near- Vertical, Resistant Sedimentary Rock
Chapter 16 Landscape Evolution: Geomorphology Topography is a Balance Between Erosion and Tectonic Uplift 1 Topography is a Balance Between Erosion and Tectonic Uplift 2 Relief • The relief in an area is the maximum difference between the highest and lowest elevation. – We have about 7000 feet of relief between Boulder and the Continental divide. Relief 3 Mountains and Valleys • A mountain is a large mass of rock that projects above surrounding terrain. • A mountain range is a continuous area of high elevation and high relief. • A valley is an area of low relief typically formed by and drained by a single stream. • A basin is a large low-lying area of low relief. In arid areas basins commonly have closed topography (no river outlet to the sea). Mountains • Typically occur in ranges. • Glaciated forms –Horn –Arête • Desert Mountains – Vertical Cliffs – Alluvial Fans 4 Mountain Landforms: Horn Deserts: Vertical Cliffs and Alluvial Fans 5 Valleys and Basins • River Valleys – U-shape (Glacial) – V-shape (Active Water erosion) – Flat-floored (depositional flood plain) • Tectonic (Fault) Valleys (Basins) – Tectonic origin – San Luis Valley – Jackson Hole – Great Basin U-shaped Valley: Glacial Erosion 6 V-shaped Valley: Active water erosion Flat-floored Valley: Depositional Flood Plain 7 Desert and Semi-arid Landforms • A plateau is a broad area of uplift with relatively little internal relief. • A mesa is a small (<10 km2)plateau bounded by cliffs, commonly in an area of flat-lying sedimentary rocks. • A butte is a small (<1000m2) hill bounded by cliffs Plateau, Mesa, Butte 8 Colorado National Monument Canyonlands 9 Desert and Semi-arid Landforms • A cuesta is an asymmetric ridge in dipping sedimentary rocks as the Flatirons. -

Corte Madera
CORTE MADERA Community Profile: Corte Madera Corte Madera is a primarily residential community IMPACTS AT-A-GLANCE: SCENARIO 6 with several large commercial areas that take advantage of the highway corridor. These 1,500+ living units 9,500+ people commercial areas serve the entire region and include outdoor malls, auto dealerships, restaurants, 994 acres exposed 79 commercial and other local business. In the near-term, 230 16 miles of roads parcels acres could be exposed to sea level rise. By the long-term, 906 acres could be exposed to sea level Storm, tidal, and Corte Madera rise and 994 acres could be exposed with an subsidence impacts Caltrans additional 100-year storm surge. Key vulnerabilities already occur Central Marin PD in Corte Madera include: Corte Madera Fire $1.4 billion worth of CHP Homes along the tributaries to Corte Madera assessed property value; Larkspur-Corte Creek may be vulnerable in the near-term. assets vulnerable; $1.5 Madera School Commercial areas on Paradise Drive may be billion in single family District vulnerable to sea level rise in the near-term, and market value189 HOAs storm surges sooner. Property Owners Segments of the 101 could be vulnerable to seasonal storm surges in the near-term, and sea level rise in the medium to long-terms. Access to the community from the US Highway 101 Map 77. Corte Madera Sea Level Rise and corridor may become increasingly difficult with 100-year Storm Surge Scenarios chronic flooding. Marin Country Day School, Marin Montessori, Cove Elementary, and Neil Cummins elementary could be vulnerable across the scenarios. -

Sutter Butte Flood Control Agency Strategic Plan April 2018 1.0
Sutter Butte Flood Control Agency Strategic Plan April 2018 1.0 Introduction The Sutter-Butte Basin (Basin) covers 300 square miles bordered by the Cherokee Canal to the north, the Sutter Buttes to the west, the Sutter Bypass to the southwest and the 44-mile long Feather River to the east—see Figure 1. The Basin is home to 95,000 residents and encompasses $7 billion of damageable assets (as estimated by the U.S. Army Corps of Engineers, or USACE). The region has sustained numerous floods, including the 1955 levee failure on the Feather River, which resulted in the deaths of at least 38 people. The personal safety and economic stability of large segments of the population are reliant on flood management systems that, until recent efforts, did not begin to meet modern engineering standards. Numerous projects and programs have been implemented in the Basin over the years to reduce flood risk, including the Feather River West Levee Project, which is nearing completion. The Sutter Butte Flood Control Agency (SBFCA) leads the planning and implementation efforts in the Basin to reduce the risk of catastrophic, riverine flooding. In this role, SBFCA collaborates with local, regional, state, tribal and federal agencies and organizations. On January 13, 2016 the SBFCA Board of Directors adopted the Strategic Plan to guide these efforts. This version is the first update to the Strategic Plan. 2.0 Purpose of the Strategic Plan The purpose of the Strategic Plan is to help formulate and articulate a vision for flood management within the Basin and to describe an approach to achieve this vision. -

2019 Pleasure-Way Brochure 1
FROM THE CEO My name is Dean Rumpel and I am CEO of Pleasure-Way At Pleasure-Way, we recognize the extraordinary Industries Ltd. I have been involved with Pleasure-Way people who build our motorhomes. It is the incredible from the very beginning and I am proud to say I have efforts of our employees that have made Pleasure- worked my way up through the ranks over the years. Way unsurpassed in the industry. Their dedication and My family has been invested in the RV industry since commitment to quality is evident in every detail of our 1968 when my father, Merv Rumpel, opened his own coaches and in our incomparable customer service. RV dealership. In 1986, he decided that he could build a better, higher-quality camper van than what he was We strive to build the perfect coach for our owners seeing in the market and Pleasure-Way was born. Merv’s so they can rest easy knowing they made the right vision of a luxury product with innovative features and purchasing decision. Whether you are a current or superior quality led to the company’s humble beginnings. potential owner, you know we have a vested interest in your satisfaction, and providing you with the best The cornerstone of Pleasure-Way is my father’s old- ownership experience possible. fashioned work ethic, pride in craftsmanship and a “customer comes first” approach to business. We remain committed to follow these principles today. I am proud to say that Pleasure-Way is still a family-owned Dean Rumpel and operated company with three generations involved CEO, Pleasure-Way Industries Ltd. -
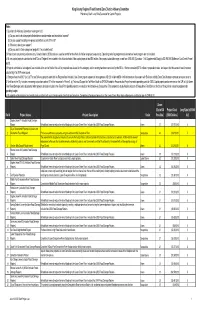
Preliminary Draft Levy Rate Scenarios for Capital Projects
King County Regional Flood Control Zone District Advisory Committee Preliminary Draft: Levy Rate Scenarios for Capital Projects Notes: 1. Questions for Advisory Committee meeting on 6/22: (a) Do you want to include projects that address coastal erosion and inundation hazards? (b) Do you support including new project submittals as part of this list? (c) What levy rate do you support? (d) Do you want to fund subregional projects? If so, at what level? 2. Project costs are planning estimates only. Constant dollar (2006) costs are used to control for the effect of inflation on project sequencing. Operating costs for programmatic elements of work program are not included. 3. All new capital projects submitted to the BTCs as 'Regional' are included in this list and shaded. New capital projects total $55 million. New project submittals range in cost from $100,000 (Carnation - Tolt Supplemental Study) to $21,900,000 (Bellevue- Coal Creek Phase 1 and 2). 4. Projects submitted as 'subregional' are included at the end of this list. No call for proposals was issued for this category, and no scoring has been conducted by the BTCs. We have received $57.8 million in proposals to date, and expect that this amount would increase substantially if an RFP were issued. 5. Changes from the 6/8/07 List: (a) The two Bellevue projects submitted as 'Regional' are included. Coal Creek project sequenced in two phases of $12.5 million and $9.4 million based on discussions with Bellevue staff (b) Dorre Don Meanders phased to reduce costs to $7.5 million in the 10-yr window, remaining acquisition costs of $7 million assumed in Phase 2. -

A Geomorphic Classification System
A Geomorphic Classification System U.S.D.A. Forest Service Geomorphology Working Group Haskins, Donald M.1, Correll, Cynthia S.2, Foster, Richard A.3, Chatoian, John M.4, Fincher, James M.5, Strenger, Steven 6, Keys, James E. Jr.7, Maxwell, James R.8 and King, Thomas 9 February 1998 Version 1.4 1 Forest Geologist, Shasta-Trinity National Forests, Pacific Southwest Region, Redding, CA; 2 Soil Scientist, Range Staff, Washington Office, Prineville, OR; 3 Area Soil Scientist, Chatham Area, Tongass National Forest, Alaska Region, Sitka, AK; 4 Regional Geologist, Pacific Southwest Region, San Francisco, CA; 5 Integrated Resource Inventory Program Manager, Alaska Region, Juneau, AK; 6 Supervisory Soil Scientist, Southwest Region, Albuquerque, NM; 7 Interagency Liaison for Washington Office ECOMAP Group, Southern Region, Atlanta, GA; 8 Water Program Leader, Rocky Mountain Region, Golden, CO; and 9 Geology Program Manager, Washington Office, Washington, DC. A Geomorphic Classification System 1 Table of Contents Abstract .......................................................................................................................................... 5 I. INTRODUCTION................................................................................................................. 6 History of Classification Efforts in the Forest Service ............................................................... 6 History of Development .............................................................................................................. 7 Goals