DOCSLIB.ORG

Chemistry 192 Problem Set 11 Spring, 2020

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chemistry 192 Problem Set 11 Spring, 2020 Chemistry 192 Problem Set 11 Spring, 2020 1. In problem set 10 we found the reaction 2N2O5(g) −! 4NO2(g) + O2(g) −1 to be first order in N2O5 with a rate constant 0.174 min at 298K. If the concentration of N2O5 is 0.357 M at time t = 0, determine that time at which the concentration of N2O5 would be 0.100 M. 2. Problem 23, page 968, textbook. 3. The gas-phase decomposition of sulfuryl chloride into sulfur dioxdie and chlorine gas proceeds according to the reaction SO2Cl2(g) −! SO2(g) + Cl2(g) and is first order in SO2Cl2. At time t = 0 pure SO2Cl2 is placed in a reaction vessel, and the total pressure is measured to be 1.107 bar. As a function of time the following data are obtained for the total pressure as a function of time Time (hours) 0 3.00 Pressure (bar) 1.107 1.479 Calculate the rate constant for the reaction. 4. Nitrogen pentoxide decomposes according to the reaction 2N2O5(g) −! 4NO2(g) + O2(g) This reaction is found to be first order with respect to N2O5(g) with a rate constant k = 4:8 × 10−4s−1. (a) What is the half-life of the reaction? 1 (b) Initially, 1.0 bar of pure N2O5(g) are introduced into a reaction vessel. Calculate the total pressure in the vessel after 1000 seconds. 5. In the gas phase at 470.K, acetic anhydride [(CH3CO)2O] decomposes into ethenone (C2H2O) and acetic acid (CH3COOH) according to the balanced reaction (CH3CO)2O(g) −! C2H2O(g) + CH3COOH(g): The decomposition of acetic anhydride obeys first-order kinetics with a rate constant k = 2:90 × 10−4 s−1 at 470.K. Pure gas-phase acetic anhydride is placed in a container of fixed volume at 470.K and the initial pressure is measured to be 2.25 bar. Calculate the total pressure in the container after 1000. seconds has elapsed. 6. The gas-phase decomposition of ethylene oxide into gas-phase methane and carbon monoxide C2H4O(g) −! CH4(g) + CO(g) −4 −1 is found to be first order in C2H4O with a rate constant k = 2:05×10 s at 298K. A container of fixed volume is filled with pure C2H4O. After the decomposition reaction proceeds for 1253. seconds the total pressure in the container is found to be PT =3.09 bar. Calculate the initial pressure in the container before the reaction has begun. 7. The gas-phase decomposition reaction of nitrous oxide (laughing gas) 1 N O −! N + O 2 (g) 2(g) 2 2(g) is first-order in N2O; i.e. R = k[N2O], where R is the rate. At 1000.K, pure nitrous oxide is placed in a container of fixed volume with an initial total pressure of 1.00 bar. After 2.00 seconds, the total pressure rises to 1.39 bar. Calculate the first-order rate constant for the decomposition of nitrous oxide at 1000.K. 8. The reaction CH3CH(OH)CHCH2 −! H2O + CH3CHCHCH2 is found to be first order in CH3CH(OH)CHCH2 with an activation energy of 241 kJ mol−1. By what factor is the rate of this reaction increased if the temperature is raised from 25◦C to 100◦C? 9. The decomposition of ethylene oxide into methane and carbon dioxide in the gas phase (CH2)2O(g) −! CH4(G) + CO(g) 3 is found to follow first-order kinetics with a half life of t1=2 = 3:38 × 10 s at 688. K 2 and a half life of t1=2 = 1:53 × 10 s at 750.K. Assuming Arrhenius behavior calculate the activation energy and the pre-exponential for the reaction. 2 10. For the reaction at 508K HI(g) −! 1=2H2(g) + 1=2I2(g) the half-life is 135 minutes when the initial HI pressure is .1 bar and 13.5 minutes when the pressure is 1.0 bar. Show that the reaction is second order. 11. The gas-phase reaction NO2(g) + CO(g) −! NO(g) + CO2(g) obeys second-order kinetics d[NO ] − 2 = k[NO ]2: dt 2 At 298.K the half life of nitrogen dioxide is measured to be 0.198 minutes when the initial concentration is 2.00 M and the half life is measured to be 7.00 ×10−2 minutes at 310.K when the initial concentration is 3.00 M. Calculate the activation energy of the reaction and determine the pre-exponential. 12. The decomposition of sulfuryl chloride in the gas phase SO2Cl2(g) −! SO2(g) + Cl2(g) 5 ◦ 2 is first order in SO2Cl2 with measured half lives of 2:3 × 10 s at 600. K and 5:4 × 10 s at 700.◦K. Calculate the activation energy for the reaction. 13. The rate law for the gas-phase reaction NO2(g) + CO(g) −! NO(g) + CO2(g) is d[NO ] − 2 = k[NO ]2: dt 2 At 350K the rate constant for the reaction is measured to be 29.0 M−1min−1 and at −1 −1 375K the rate constant is found to be 73.7 M min . Calculate the half life of NO2 for the reaction at T =362K when the initial concentration of NO2 is 2.75 M. 14. The gas-phase reaction N2O4(g) −! 2NO2(g) is first order in dinitrogen tetroxide, N2O4. The half life of dinitrogen tetroxide is 1.36 ×10−7 s at 303K and 3:61 × 10−8 s at 323 K. A container is filled with pure dinitrogen tetroxide gas at 315 K with an initial concentration of 2.50 M. Calculate −7 the concentration of NO2(g) at 315 K, 1:00 × 10 s after the pure N2O4 gas has been placed in the container. 3 15. What activation energy implies a reaction rate to be doubled for a 10◦C temperature rise from 25◦C to 35◦C? 16. The reaction 2O3(g) −! 3O2(g) is believed to follow the following mechanism: k1 O3(g) −! O2(g) + Og k−1 O2(g) + Og −! O3(g) k O3(g) + O(g) −! 2O2(g) (slow) Use the steady-state approximation for the concentration of O to determine the rate law implied by this mechanism. What is the order of the reaction and the molecularity of the slow step? 17. The proposed mechanism for the gas-phase reaction 2NO(g) + H2(g) −! N2O(g) + H2O(g) is k1 fast 2NO(g) −! N2O2(g) k−1 fast N2O2(g) −! 2NO(g) k2 slow N2O2(g) + H2(g) −! N2O(g) + H2O(g): Derive the rate law associated with the mechanism, and simplify the rate law using the relation k−1 >> k2[H2]. Give the order of the reaction and the molecularity of the slow step. 18. The gas-phase reaction 1 N O −! 2NO + O 2 5(g) 2(g) 2 2(g) is believed to occur by the following mechanism: k1 N2O5(g) −! NO2(g) + NO3(g) (fast) k−1 NO2(g) + NO3(g) −! N2O5(g) (fast) k2 NO2(g) + NO3(g) −! NO2(g) + O2(g) + NO(g) (slow) k3 NO(g) + N2O5(g) −! 3NO2(g) (fast): Derive the rate law associated with this mechanism. 4 19. A proposed mechanism for the balanced gas-phase reaction 2NO(g) + O2(g)) −! 2NO2(g) is k1 NO(g) + O2(g) −! NO3(g) fast k−1 NO3(g) −! NO(g) + O2(g) fast k2 NO(g) + NO3(g) −! 2NO2(g) slow Use the steady-state approximation on the reactive intermediate to deduce the rate law implied by the proposed mechanism. 5.
Load more

Recommended publications
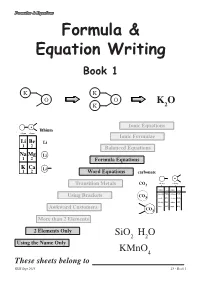
  • Formula & Equation Writing
    Formulae & Equations Formula & Equation Writing Book 1 K K O O K O K 2 Ionic Equations lithium column column 1 2 Ionic Formulae Li Be Li 1 2 Balanced Equations Na Mg Li 1 2 Formula Equations K Ca Li 1 2 Word Equations carbonate valency valency Transition Metals CO3 1 2 name formula name formula ammonium NH4 carbonate CO3 Using Brackets CO 3 cyanide CN chromate CrO4 hydroxide OH sulphate SO4 nitrate NO sulphite SO Awkward Customers 3 3 CO3 More than 2 Elements 2 Elements Only SiO2 H2O Using the Name Only KMnO4 These sheets belong to KHS Sept 2013 page 1 S3 - Book 1 Formulae & Equations What is a Formula ? The formula of a compound tells you two things about the compound :- SiO H O i) which elements are in the compound 2 2 using symbols, and KMnO4 ii) how many atoms of each element are in the compound using numbers. Test Yourself What would be the formula for each of the following? Br H Cl K H C S Al Br O H Cl K H Br Using the Name Only Some compounds have extra information in their carbon monoxide names that allow people to work out and write CO the correct formula. carbon dioxide CO2 The names of the elements appear as usual but dinitrogen tetroxide N O this time the number of each type of atom is 2 4 included using mono- = 1 di- = 12 tri- = 3 tetra- = 4 penta- = 5 hexa- =46 Test Yourself 1 What would be the formula for each of the following? 1.
    [Show full text]
  • Nitric Acid Plants (PDF)
    Office of Air and Radiation December 2010 AVAILABLE AND EMERGING TECHNOLOGIES FOR REDUCING GREENHOUSE GAS EMISSIONS FROM THE NITRIC ACID PRODUCTION INDUSTRY Available and Emerging Technologies for Reducing Greenhouse Gas Emissions from the Nitric Acid Production Industry Prepared by the Sector Policies and Programs Division Office of Air Quality Planning and Standards U.S. Environmental Protection Agency Research Triangle Park, North Carolina 27711 December 2010 Table of Contents Abbreviations and Acronyms p.1 I Introduction /Purpose of this Document p.2 II. Description of the Nitric Acid Production Process p.3 A. Weak Nitric Acid Production p.3 B. High-Strength Nitric Acid Production p.6 III. N2O Emissions and Nitric Acid Production Process p. 7 IV. Summary of Control Measures p.9 A. Primary Controls p.10 B. Secondary Control p.11 C. Tertiary Controls p.13 D. Selective Catalytic Reduction p.16 V. Other Greenhouse Gas Emissions p.16 VI. Energy Efficiency Improvements p.17 VII. EPA Contacts p.19 VIII. References p.20 Appendix A – Southeast Idaho Energy p.23 Appendix B - US Nitric Acid Plants p.24 Appendix C – CDM Monitoring Reports p.25 Abbreviations and Acronyms atm Pressure in atmospheres BACT Best Available Control Technologies Btu British Thermal Unit Btu/lb Btu per lb of 100% nitric acid CAR Climate Action Reserve CDM Clean Development Mechanism CHP Combined Heat and Power CO2 Carbon dioxide CO2e Carbon dioxide equivalent EU European Union GHG Greenhouse Gases H2 Hydrogen IPCC Intergovernmental Panel on Climate Change IPPC Industrial Pollution Prevention and Control JI Joint Implementation kg N2O/tonne kilograms of N2O per tonne of 100% nitric acid kg CO2e/tonne kilograms of CO2e per tonne of 100% nitric acid lb N2O/ton pounds of N2O per ton of 100% nitric acid N2 Nitrogen NH3 Ammonia NO Nitric oxide NO2 Nitrogen dioxide NOx Nitrogen oxides NSCR Nonselective Catalytic Reduction N2 O4 Nitrogen tetraoxide N2O Nitrous oxide O2 Oxygen PSD Prevention of Significant Deterioration SCR Selective Catalytic Reduction TPD Tons per day 1 I.
    [Show full text]
  • Binary Covalent Common Names
    Binary Covalent Common Names – H2O, water – NH3, ammonia – CH4, methane – C2H6, ethane – C3H8, propane – C4H10, butane – C5H12, pentane – C6H14, hexane Naming Binary Covalent CompounDs • If the subscript for the first element is greater than one, inDicate the subscript with a prefix. – We Do not write mono- on the first name. – Leave the "a" off the enD of the prefixes that enD in "a" anD the “o” off of mono- if they are placeD in front of an element that begins with a vowel (oxygen or ioDine). Prefixes mon(o) hex(a) di hept(a) tri oct(a) tetr(a) non(a) pent(a) dec(a) Nitrogen OxiDe Names • N2O3 – name starts with di • N2O5 – name starts with di • NO2 – no initial prefix • NO – no initial prefix Naming Binary Covalent CompounDs • Follow the prefix with the name of the first element in the formula. – N2O3 – dinitrogen – N2O3 – dinitrogen – NO2 – nitrogen – NO – nitrogen Naming Binary Covalent CompounDs • Write a prefix to inDicate the subscript for the seconD element. (Remember to leave the “o” off of mono- anD the “a” off of the prefixes that enD in “a” when they are placeD in front of a name that begins with a vowel.) – N2O3 – dinitrogen tri – N2O5 – dinitrogen pent – NO2 – nitrogen di – NO – nitrogen mon Naming Binary Covalent CompounDs • Write the root of the name of the seconD symbol in the formula. (See the next sliDe.) – N2O3 – dinitrogen triox – N2O5 – dinitrogen pentox – NO2 – nitrogen diox – NO – nitrogen monox Roots of Nonmetals H hydr- F fluor- C carb- Cl chlor- N nitr- Br brom- P phosph- I iod- O ox- S sulf- Se selen- Naming Binary Covalent CompounDs • AdD -ide to the enD of the name.
    [Show full text]
  • Modeling the Vapor – Liquid Equilibrium and Association
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Open Archive Toulouse Archive Ouverte MODELING THE VAPOR – LIQUID EQUILIBRIUM AND ASSOCIATION OF NITROGEN DIOXIDE / DINITROGEN TETROXIDE AND ITS MIXTURES WITH CARBON DIOXIDE A. Belkadi 1,2 , F. Llovell 3, V. Gerbaud 1*, L. F. Vega 2,3*,+ 1Université de Toulouse, LGC (Laboratoire de Génie Chimique), CNRS, INP, UPS, 5 rue Paulin Talabot, F-31106 Toulouse Cedex 01 – France 2MATGAS Research Center, Campus UAB. 08193 Bellaterra, Barcelona Spain 3Institut de Ciència de Materials de Barcelona, (ICMAB-CSIC), Consejo Superior de Investigaciones Científicas, Campus de la UAB, 08193 Bellaterra, Barcelona, Spain * Corresponding authors: [email protected], [email protected]. +Present address: Carburos Metálicos-Grup Air Products. C/ Aragón 300. 08009 Barcelona. Spain. 1 Abstract We have used in this work the crossover soft-SAFT equation of state to model nitrogen dioxide/dinitrogen tetraoxide (NO 2/N 2O4), carbon dioxide (CO 2) and their mixtures. The prediction of the vapor – liquid equilibrium of this mixture is of utmost importance to correctly assess the NO 2 monomer amount that is the oxidizing agent of vegetal macromolecules in the CO 2 + NO 2 / N 2O4 reacting medium under supercritical conditions. The quadrupolar effect was explicitly considered when modeling carbon dioxide, enabling to obtain an excellent description of the vapor-liquid equilibria diagrams. NO 2 was modeled as a self associating molecule with a single association site to account for the strong associating character of the NO 2 molecule. Again, the vapor- liquid equilibrium of NO 2 was correctly modeled.
    [Show full text]
  • Nitrogen Oxides (Nox), Why and How They Are Controlled
    United States Office of Air Quality EPA 456/F-99-006R Environmental Protection Planning and Standards November 1999 Agency Research Triangle Park, NC 27711 Air EPA-456/F-99-006R November 1999 Nitrogen Oxides (NOx), Why and How They Are Controlled Prepared by Clean Air Technology Center (MD-12) Information Transfer and Program Integration Division Office of Air Quality Planning and Standards U.S. Environmental Protection Agency Research Triangle Park, North Carolina 27711 DISCLAIMER This report has been reviewed by the Information Transfer and Program Integration Division of the Office of Air Quality Planning and Standards, U.S. Environmental Protection Agency and approved for publication. Approval does not signify that the contents of this report reflect the views and policies of the U.S. Environmental Protection Agency. Mention of trade names or commercial products is not intended to constitute endorsement or recommendation for use. Copies of this report are available form the National Technical Information Service, U.S. Department of Commerce, 5285 Port Royal Road, Springfield, Virginia 22161, telephone number (800) 553-6847. CORRECTION NOTICE This document, EPA-456/F-99-006a, corrects errors found in the original document, EPA-456/F-99-006. These corrections are: Page 8, fourth paragraph: “Destruction or Recovery Efficiency” has been changed to “Destruction or Removal Efficiency;” Page 10, Method 2. Reducing Residence Time: This section has been rewritten to correct for an ambiguity in the original text. Page 20, Table 4. Added Selective Non-Catalytic Reduction (SNCR) to the table and added acronyms for other technologies. Page 29, last paragraph: This paragraph has been rewritten to correct an error in stating the configuration of a typical cogeneration facility.
    [Show full text]
  • The Chemistry of Solvated Nitric Oxide
    The Chemistry of Solvated Nitric Oxide: As the Free Radical and as Super-saturated Dinitrogen Trioxide Solutions By Kristopher A. Rosadiuk March, 2015 A thesis submitted to McGill University in partial fulfillment of the requirements in the degree of: DOCTORATE OF PHILOSOPHY Department of Chemistry, Faculty of Science McGill University Montreal, Quebec, Canada © Kristopher Rosadiuk, 2015. Abstract The unusual behaviour of the mid-oxidation state nitrogen oxides, nitric oxide (NO) and dinitrogen trioxide (N2O3), are explored in solution. Nitric oxide is shown to catalyze the cis-trans isomerizations of diazo species in aqueous and organic solutions, and a model is presented by which this proceeds by spin catalysis, making use of the unpaired electron of NO to permit access to triplet patways. Five diazo compounds are tested and compared to stilbene, which is not found to isomerize under these conditions. Dinitrogen trioxide is found to form easily in organic solvents, which stabilize the molecule even above room temperature. Solutions can be formed at chemically useful concentrations and levels of purity, and this result is compared with the sparse literature concerning this phenomenon. The chemistry of these solutions at 0˚C is surveyed extensively, with 23 distinct organic reactions and 15 inorganic reactions being described. The first reported room temperature adduct of dinitrogen trioxide is presented, as well as novel syntheses for nitrosyl chloride and nitrosylsulfuric acid. X-ray structures are also given for a previously reported benzoquinone-phenol adduct, as well as a new mixed valent-mercury nitride salt of the form Hg4N4O9. Résumé Le comportement inhabituel des oxydes d'azote aux états d’oxydations moyens, comme l’oxyde nitrique (NO) et le trioxyde dinitrique (N2O3), est exploré en solution.
    [Show full text]
  • The Weakly Bound Dinitrogen Tetroxide Molecule: High Level Single Reference Wavefunctions Are Good Enough
    The weakly bound dinitrogen tetroxide molecule: High level single reference wavefunctions are good enough Cite as: J. Chem. Phys. 106, 7178 (1997); https://doi.org/10.1063/1.473679 Submitted: 18 November 1996 . Accepted: 23 January 1997 . Published Online: 04 June 1998 Steve S. Wesolowski, Justin T. Fermann, T. Daniel Crawford, and Henry F. Schaefer III ARTICLES YOU MAY BE INTERESTED IN Reinvestigation of the Structure of Dinitrogen Tetroxide, N2O4, by Gaseous Electron Diffraction The Journal of Chemical Physics 56, 4541 (1972); https://doi.org/10.1063/1.1677901 The gas-phase structure of the asymmetric, trans-dinitrogen tetroxide (N2O4), formed by dimerization of nitrogen dioxide (NO2), from rotational spectroscopy and ab initio quantum chemistry The Journal of Chemical Physics 146, 134305 (2017); https://doi.org/10.1063/1.4979182 The Infrared Absorption Spectra of NO2 and N2O4 The Journal of Chemical Physics 1, 507 (1933); https://doi.org/10.1063/1.1749324 J. Chem. Phys. 106, 7178 (1997); https://doi.org/10.1063/1.473679 106, 7178 © 1997 American Institute of Physics. The weakly bound dinitrogen tetroxide molecule: High level single reference wavefunctions are good enough Steve S. Wesolowski, Justin T. Fermann,a) T. Daniel Crawford, and Henry F. Schaefer III Center for Computational Quantum Chemistry, University of Georgia, Athens, Georgia 30602 ~Received 18 November 1996; accepted 23 January 1997! Ab initio studies of dinitrogen tetroxide ~N2O4! have been performed to predict the equilibrium geometry, harmonic vibrational frequencies, and fragmentation energy ~N2O4 2NO2!. The structure was optimized at the self-consistent field, configuration interaction, and→ coupled-cluster levels of theory with large basis sets.
    [Show full text]
  • Safety Data Sheet
    SDS – Copper and Nickel Base Bare Wire and Strip Electrodes and Rods Revision 11 Issue Date – July, 2013 SAFETY DATA SHEET SECTION 1: PRODUCT AND COMPANY IDENTIFICATION Manufacturer/Supplier Name: Sandvik Wire and Heating Technologies Address: P.O. Box 1220, Scranton, PA 18501-1220 Phone Number: (570) 585-7500 Trade Name: SANDVIK Classification: AWS A5.14/ASME SFA 5.14, ASME SFA 5.14 Section III, MIL-E-21562, AWS A5.7/ASME SFA 5.7, ASME SFA 5.7 Section III. Product Type: Copper and Nickel Alloyed Bare Wire, Strip Electrodes and Rod for Manual, Semi-automatic, and Automatic Welding Processes. Product Identifiers: NiCr3H, NiCr-3, NiCrMo-3, NiCu-7, NiCrMo-4, NiCrMo-11, NiCrMo-10 SECTION 2: HAZARDS IDENTIFICATION Copper and Nickel alloyed bare wire and strip electrodes and rod are welding consumables which are either solid wire or strip. EMERGENCY OVERVIEW Effects of Over-exposure: Electric arc welding may create one or more of the following health hazards: FUMES AND GASES can be dangerous to your health. SHORT-TERM (acute) OVEREXPOSURE to welding fumes may result in discomfort, such as dizziness, nausea, or dryness or irritation of nose, throat, or eyes. LONG-TERM (chronic) OVEREXPOSURE to welding fumes can lead to siderosis (iron deposits in lungs), central nervous system, liver or kidney damage, skin and respiratory sensitization (allergic reaction), and is believed by some investigators to affect pulmonary function. PRIMARY ROUTE OF ENTRY is the respiratory system. MEDICAL CONDITIONS AGGRAVATED BY EXPOSURE: Pre-existing eye, respiratory or allergic conditions. ARC RAYS can injure eyes and burn skin.
    [Show full text]
  • Nitrogen Dioxide NO2 and N2O4 Safety Data Sheet SDS P4633
    Dinitrogen Tetroxide (Nitrogen dioxide) Safety Data Sheet P-4633 This SDS conforms to U.S. Code of Federal Regulations 29 CFR 1910.1200, Hazard Communication. Date of issue: 01/01/1979 Revision date: 10/21/2016 Supersedes: 01/07/2016 SECTION: 1. Product and company identification 1.1. Product identifier Product form : Substance Name : Dinitrogen Tetroxide (Nitrogen dioxide) CAS No : 10102-44-0 Formula : NO2 Other means of identification : Nitrito, Nitrogen oxide, Nitrogen peroxide, nitrogen tetroxide, NTO, red oxide of nitrogen 1.2. Relevant identified uses of the substance or mixture and uses advised against Use of the substance/mixture : Industrial use. Use as directed. 1.3. Details of the supplier of the safety data sheet Praxair, Inc. 10 Riverview Drive Danbury, CT 06810-6268 - USA T 1-800-772-9247 (1-800-PRAXAIR) - F 1-716-879-2146 www.praxair.com 1.4. Emergency telephone number Emergency number : Onsite Emergency: 1-800-645-4633 CHEMTREC, 24hr/day 7days/week — Within USA: 1-800-424-9300, Outside USA: 001-703-527-3887 (collect calls accepted, Contract 17729) SECTION 2: Hazard identification 2.1. Classification of the substance or mixture GHS-US classification Ox. Gas 1 H270 Liquefied gas H280 Acute Tox. 1 (Inhalation:gas) H330 Skin Corr. 1B H314 Eye Dam. 1 H318 2.2. Label elements GHS-US labeling Hazard pictograms (GHS-US) : GHS03 GHS04 GHS05 GHS06 Signal word (GHS-US) : DANGER Hazard statements (GHS-US) : H270 - MAY CAUSE OR INTENSIFY FIRE; OXIDIZER H280 - CONTAINS GAS UNDER PRESSURE; MAY EXPLODE IF HEATED H314 - CAUSES SEVERE SKIN
    [Show full text]
  • 7-N2O4 Tank Cleaning Work Plan
    Imagine the result and MISSISSIPPI BLUFFS INDUSTRIAL PARK, LLC Dinitrogen Tetroxide Tank Cleaning Work Plan Former Vicksburg Chemical Company Vicksburg, Mississippi 13 January 2009 Dinitrogen Tetroxide Tank Cleaning Work Plan Former Vicksburg Chemical Craig A. Derouen, P.E. Company Senior Engineer Vicksburg, Mississippi David R. Escudé, P.E. Vice President/Principal Engineer Prepared for: Mississippi Department of Environmental Quality and Mississippi Bluffs Industrial Park, LLC Prepared by: ARCADIS 10352 Plaza Americana Drive Baton Rouge Louisiana 70816 Tel 225 292 1004 Fax 225 218 9677 Our Ref.: LA002656.0001.00026 Date: 13 January 2009 This document is intended only for the use of the individual or entity for which it was prepared and may contain information that is privileged, confidential, and exempt from disclosure under applicable law. Any dissemination, distribution, or copying of this document is strictly prohibited. Table of Contents 1. Introduction and Work Plan Rationale 1 1.1 Objectives/Rationale 1 1.2 Background 1 1.2.1 Property Location 1 1.2.2 Dinitrogen Tetroxide Site History 1 1.3 Work Plan Approach 2 F 2. Properties of Dinitrogen Tetroxide 2 2.1 Physical Properties 3 2.2 Chemical Properties 3 2.3 Toxicity Characteristics 3 I 2.4 Regulatory Considerations 3 3. Health and Safety Precautions 4 4. Treatment Process 4 N 4.1 N2O4 and NO2 Treatment 4 4.2 Tank Cleaning 6 5. Tank Cleaning Derived Wastes 6 A Figures 1 Site Location Map 2 Former Plant Process Areas 3 Conceptualized Treatment Schematic L Appendices A USEPA Pollution Reports B USEPA Tank List (Partial) C NTSB Hazardous Materials Accident Brief D Selected Published Guidance on N2O4 Mississippi Bluffs/2656.1.26/R/7/egp i Dinitrogen Tetroxide Tank Cleaning Work Plan Former Vicksburg Chemical Company Vicksburg, Mississippi 1.
    [Show full text]
  • Adsorption Equilibrium of Nitrogen Dioxide and Dinitrogen
    Electronic Supplementary Material (ESI) for Physical Chemistry Chemical Physics. This journal is © the Owner Societies 2018 ADSORPTION EQUILIBRIUM OF NITROGEN DIOXIDE AND DINITROGEN TETROXIDE IN POROUS MATERIALS I. Matito-Martosa, A. Rahbarib, A. Martin-Calvoc, D. Dubbeldamd, T.J.H. Vlugtb, and S. Calero*a aDepartment of Physical, Chemical and Natural Systems, University Pablo de Olavide, Sevilla 41013, Spain bProcess and Energy Department, Delft University of Technology, Leeghwaterstraat 39, 2628CB Delft, The Netherlands cDepartment of Chemical Engineering, Vrije Universiteit Brussel, Brussels, 1050, Belgium dVan ’t Hoff Institute for Molecular Sciences, University of Amsterdam, Science Park 904, 1098XH Amsterdam, The Netherlands Supporting Information Table S1 Structural and topological properties of the zeolites under study. Pore Surface Density Channel Channel Channel Channel Ring Zeolite Volume area (kgm3) System Diameter Diameter Diameter sizes (cm3g) (m^2/g) FER 0.066 235.07 1837.87 2D (1D) 4.69 3.4 - 10 8 6 5 TON 0.091 301.41 1968.716 1D 5.11 - - 10 6 5 MOR 0.15 477.92 1711.056 1D 6.45 - - 12 8 5 4 MFI 0.164 547.67 1796.342 3D 4.7 4.46 4.46 10 6 5 4 FAU 0.332 1020.88 1342.047 3D - Cages 7.35 7.35 7.35 12 6 4 Table S2 Mole fraction of NO2 and N2O4 for the bulk phase reaction dimerization over a temperature range of 273-404 K and a pressure range of 0.1-5 atm. The table shows the results obtained in this work from RxMC simulations in the NPT ensemble and calculated data from Chao et al.32 for direct comparison.
    [Show full text]
  • Ionic & Covalent Compound Naming Race
    Name __________________________ Date ___________ Period _________ Ionic & Covalent Compound Naming Race First, identify whether these compounds are ionic or covalent. Then, use the correct formula writing rules to write the correct chemical formulas for each compound. Type of Compound: Compound Name Chemical Formula Ionic or Covalent 1) copper (II) chlorite 2) sodium hydroxide 3) nitrogen dioxide 4) cobalt (III) oxalate 5) ammonium sulfide 6) aluminum cyanide 7) carbon disulfide 8) tetraphosphorous pentoxide 9) potassium permanganate 10) manganese (III) chloride Type of Compound: Compound Name Chemical Formula Ionic or Covalent 11) calcium bromate 12) carbon monoxide 13) potassium oxide 14) antimony tribromide 15) zinc phosphate 16) copper (II) bicarbonate 17) dinitrogen tetroxide 18) manganese (IV) carbonate 19) lead (IV) nitride 20) pentacarbon decahydride Ionic_Covalent Names: Chapter 9 Honors Chemistry Name __________________________ Date ___________ Period _________ Ionic & Covalent Compound Naming First, identify whether these compounds are ionic or covalent. Then, use the correct naming rules to write the correct names for each compound. Chemical Formula Type of Compound: Compound Name Ionic or Covalent 21) CdBr2 22) Cr(Cr2O7)3 23) SBr2 24) (NH4)2CrO4 25) CuO 26) Pt3(PO3)4 27) Al(ClO4)3 28) NH3 29) Ca(C2H3O2)2 30) N2O Type of Compound: Chemical Formula Compound Name Ionic or Covalent 31) V(SO4)2 32) Ag2CO3 33) N2S3 34) FeSO3 35) Zn(NO2)2 36) C6H12O6 37) PCl3 38) Mn(OH)7 39) Ni(NO3)2 40) O2 Ionic_Covalent Names: Chapter 9 Honors Chemistry Name __________________________ Date ___________ Period _________ Compound Naming Race - Solutions Be the first team in the room to correctly get all the names on this sheet right.
    [Show full text]