Variation in Recombination Rate and Its Genetic Determinism in Sheep Populations
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Microarray-Based Analysis of Genes, Transcription Factors, and Epigenetic Modifications in Lung Cancer Exposed to Nitric Oxide
CANCER GENOMICS & PROTEOMICS 17 : 401-415 (2020) doi:10.21873/cgp.20199 Microarray-based Analysis of Genes, Transcription Factors, and Epigenetic Modifications in Lung Cancer Exposed to Nitric Oxide ARNATCHAI MAIUTHED 1, ORNJIRA PRAKHONGCHEEP 2,3 and PITHI CHANVORACHOTE 2,3 1Department of Pharmacology, Faculty of Pharmacy, Mahidol University, Bangkok, Thailand; 2Cell-based Drug and Health Product Development Research Unit, Faculty of Pharmaceutical Sciences, Chulalongkorn University, Bangkok, Thailand; 3Department of Pharmacology and Physiology, Faculty of Pharmaceutical Sciences, Chulalongkorn University, Bangkok, Thailand Abstract. Background/Aim: Nitric oxide (NO) is recognized NO exposure of lung cancer cells resulted in a change in as an important biological mediator that exerts several transcription factors (TFs) and epigenetic modifications human physiological functions. As its nature is an aqueous (histone modification and miRNA). Interestingly, NO soluble gas that can diffuse through cells and tissues, NO treatment was shown to potentiate cancer stem cell-related can affect cell signaling, the phenotype of cancer and modify genes and transcription factors Oct4, Klf4, and Myc. surrounding cells. The variety of effects of NO on cancer cell Conclusion: Through this comprehensive approach, the biology has convinced researchers to determine the defined present study illustrated the scheme of how NO affects mechanisms of these effects and how to control this mediator molecular events in lung cancer cells. for a better understanding as well as for therapeutic gain. Materials and Methods: We used bioinformatics and Lung cancer is one of the leading causes of cancer-related pharmacological experiments to elucidate the potential deaths worldwide (1, 2). Since the aggressive phenotypes regulation and underlying mechanisms of NO in non-small and treatment failures have been frequently observed in lung a lung cancer cell model. -

Chr CNV Start CNV Stop Gene Gene Feature 1 37261312 37269719
chr CNV start CNV stop Gene Gene feature 1 37261312 37269719 Tmem131 closest upstream gene 1 37261312 37269719 Cnga3 closest downstream gene 1 41160869 41180390 Tmem182 closest upstream gene 1 41160869 41180390 2610017I09Rik closest downstream gene 1 66835123 66839616 1110028C15Rik in region 2 88714200 88719211 Olfr1206 closest upstream gene 2 88714200 88719211 Olfr1208 closest downstream gene 2 154840037 154846228 a in region 3 30065831 30417157 Mecom closest upstream gene 3 30065831 30417157 Arpm1 closest downstream gene 3 35476875 35495913 Sox2ot closest upstream gene 3 35476875 35495913 Atp11b closest downstream gene 3 39563408 39598697 Fat4 closest upstream gene 3 39563408 39598697 Intu closest downstream gene 3 94246481 94410611 Celf3 in region 3 94246481 94410611 Mrpl9 in region 3 94246481 94410611 Riiad1 in region 3 94246481 94410611 Snx27 in region 3 104311901 104319916 Lrig2 in region 3 144613709 144619149 Clca6 in region 3 144613709 144619149 Clca6 in region 4 108673 137301 Vmn1r2 closest downstream gene 4 3353037 5882883 6330407A03Rik in region 4 3353037 5882883 Chchd7 in region 4 3353037 5882883 Fam110b in region 4 3353037 5882883 Impad1 in region 4 3353037 5882883 Lyn in region 4 3353037 5882883 Mos in region 4 3353037 5882883 Penk in region 4 3353037 5882883 Plag1 in region 4 3353037 5882883 Rps20 in region 4 3353037 5882883 Sdr16c5 in region 4 3353037 5882883 Sdr16c6 in region 4 3353037 5882883 Tgs1 in region 4 3353037 5882883 Tmem68 in region 4 5919294 6304249 Cyp7a1 in region 4 5919294 6304249 Sdcbp in region 4 5919294 -

Genetics of Arthrogryposis and Macroglossia in Piemontese Cattle Breed
animals Article Genetics of Arthrogryposis and Macroglossia in Piemontese Cattle Breed Liliana Di Stasio 1,* , Andrea Albera 2, Alfredo Pauciullo 1 , Alberto Cesarani 3 , Nicolò P. P. Macciotta 3 and Giustino Gaspa 1 1 Department of Agricultural, Forest and Food Sciences, University of Torino, Largo Baccini 2, 10095 Grugliasco (TO), Italy; [email protected] (A.P.); [email protected] (G.G.) 2 Associazione Nazionale Allevatori Bovini di Razza Piemontese, strada provinciale Trinita’ 31/A, 12061 Carrù (CN), Italy; [email protected] 3 Department of Agriculture, University of Sassari, Via De Nicola 9, 07100 Sassari, Italy; [email protected] (A.C.); [email protected] (N.P.P.M.) * Correspondence: [email protected] Received: 7 September 2020; Accepted: 18 September 2020; Published: 24 September 2020 Simple Summary: The study was carried out in order to investigate the genetic background of arthrogryposis and macroglossia in the Piemontese cattle breed, for which limited information is available so far. The genotyping of affected and healthy animals with a high-density chip and the subsequent genome-wide association study did not evidence a single strong association with the two pathologies. Therefore, for arthrogryposis, the results do not support the existence of a single-gene model, as reported for other breeds. Rather, 23 significant markers on different chromosomes were found, associated to arthrogryposis, to macroglossia, or to both pathologies, suggesting a more complex genetic mechanism underlying both diseases in the Piemontese breed. The significant single nucleotide polymorphisms (SNPs) allowed the identification of some genes (NTN3, KCNH1, KCNH2, and KANK3) for which a possible role in the pathologies can be hypothesized. -

The Hypothalamus As a Hub for SARS-Cov-2 Brain Infection and Pathogenesis
bioRxiv preprint doi: https://doi.org/10.1101/2020.06.08.139329; this version posted June 19, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC-ND 4.0 International license. The hypothalamus as a hub for SARS-CoV-2 brain infection and pathogenesis Sreekala Nampoothiri1,2#, Florent Sauve1,2#, Gaëtan Ternier1,2ƒ, Daniela Fernandois1,2 ƒ, Caio Coelho1,2, Monica ImBernon1,2, Eleonora Deligia1,2, Romain PerBet1, Vincent Florent1,2,3, Marc Baroncini1,2, Florence Pasquier1,4, François Trottein5, Claude-Alain Maurage1,2, Virginie Mattot1,2‡, Paolo GiacoBini1,2‡, S. Rasika1,2‡*, Vincent Prevot1,2‡* 1 Univ. Lille, Inserm, CHU Lille, Lille Neuroscience & Cognition, DistAlz, UMR-S 1172, Lille, France 2 LaBoratorY of Development and PlasticitY of the Neuroendocrine Brain, FHU 1000 daYs for health, EGID, School of Medicine, Lille, France 3 Nutrition, Arras General Hospital, Arras, France 4 Centre mémoire ressources et recherche, CHU Lille, LiCEND, Lille, France 5 Univ. Lille, CNRS, INSERM, CHU Lille, Institut Pasteur de Lille, U1019 - UMR 8204 - CIIL - Center for Infection and ImmunitY of Lille (CIIL), Lille, France. # and ƒ These authors contriButed equallY to this work. ‡ These authors directed this work *Correspondence to: [email protected] and [email protected] Short title: Covid-19: the hypothalamic hypothesis 1 bioRxiv preprint doi: https://doi.org/10.1101/2020.06.08.139329; this version posted June 19, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. -

Us 2018 / 0305689 A1
US 20180305689A1 ( 19 ) United States (12 ) Patent Application Publication ( 10) Pub . No. : US 2018 /0305689 A1 Sætrom et al. ( 43 ) Pub . Date: Oct. 25 , 2018 ( 54 ) SARNA COMPOSITIONS AND METHODS OF plication No . 62 /150 , 895 , filed on Apr. 22 , 2015 , USE provisional application No . 62/ 150 ,904 , filed on Apr. 22 , 2015 , provisional application No. 62 / 150 , 908 , (71 ) Applicant: MINA THERAPEUTICS LIMITED , filed on Apr. 22 , 2015 , provisional application No. LONDON (GB ) 62 / 150 , 900 , filed on Apr. 22 , 2015 . (72 ) Inventors : Pål Sætrom , Trondheim (NO ) ; Endre Publication Classification Bakken Stovner , Trondheim (NO ) (51 ) Int . CI. C12N 15 / 113 (2006 .01 ) (21 ) Appl. No. : 15 /568 , 046 (52 ) U . S . CI. (22 ) PCT Filed : Apr. 21 , 2016 CPC .. .. .. C12N 15 / 113 ( 2013 .01 ) ; C12N 2310 / 34 ( 2013. 01 ) ; C12N 2310 /14 (2013 . 01 ) ; C12N ( 86 ) PCT No .: PCT/ GB2016 /051116 2310 / 11 (2013 .01 ) $ 371 ( c ) ( 1 ) , ( 2 ) Date : Oct . 20 , 2017 (57 ) ABSTRACT The invention relates to oligonucleotides , e . g . , saRNAS Related U . S . Application Data useful in upregulating the expression of a target gene and (60 ) Provisional application No . 62 / 150 ,892 , filed on Apr. therapeutic compositions comprising such oligonucleotides . 22 , 2015 , provisional application No . 62 / 150 ,893 , Methods of using the oligonucleotides and the therapeutic filed on Apr. 22 , 2015 , provisional application No . compositions are also provided . 62 / 150 ,897 , filed on Apr. 22 , 2015 , provisional ap Specification includes a Sequence Listing . SARNA sense strand (Fessenger 3 ' SARNA antisense strand (Guide ) Mathew, Si Target antisense RNA transcript, e . g . NAT Target Coding strand Gene Transcription start site ( T55 ) TY{ { ? ? Targeted Target transcript , e . -

Expression Pattern of Olfactory Receptor Genes in Human Cumulus Cells As an Indicator for Competent Oocyte Selection
Turkish Journal of Biology Turk J Biol (2020) 44: 371-380 http://journals.tubitak.gov.tr/biology/ © TÜBİTAK Research Article doi:10.3906/biy-2003-79 Expression pattern of olfactory receptor genes in human cumulus cells as an indicator for competent oocyte selection 1 2 1,3 4 5 Neda DAEI-FARSHBAF , Reza AFLATOONIAN , Fatemeh-Sadat AMJADI , Sara TALEAHMAD , Mahnaz ASHRAFI , 3,1, Mehrdad BAKHTIYARI * 1 Department of Anatomy, Faculty of Medicine, Iran University of Medical Sciences, Tehran, Iran 2 Department of Endocrinology and Female Infertility, Reproductive Biomedicine Research Center, Royan Institute for Reproductive Biomedicine, Academic Center for Education, Culture and Research, Tehran, Iran 3 Cellular and Molecular Research Center, Faculty of Medicine, Iran University of Medical Sciences, Tehran, Iran 4 Department of Molecular Systems Biology, Cell Science Research Center, Royan Institute for Stem Cell Biology and Technology (RI-SCBT), Academic Center for Education, Culture and Research, Tehran, Iran 5 Department of Obstetrics and Gynecology, Faculty of Medicine, Iran University of Medical Sciences, Tehran, Iran Received: 26.03.2020 Accepted/Published Online: 09.09.2020 Final Version: 14.12.2020 Abstract: Odorant or olfactory receptors are mainly localized in the olfactory epithelium for the perception of different odors. Interestingly, many ectopic olfactory receptors with low expression levels have recently been found in nonolfactory tissues to involve in local functions. Therefore, we investigated the probable role of the olfactory signaling pathway in the surrounding microenvironment of oocyte. This study included 22 women in intracytoplasmic sperm injection cycle. The expression of olfactory target molecules in cumulus cells surrounding the growing and mature oocytes was evaluated by Western blotting and real-time polymerase chain reaction. -
Integrated Functional Genomic Analysis Enables Annotation of Kidney Genome-Wide Association Study Loci
BASIC RESEARCH www.jasn.org Integrated Functional Genomic Analysis Enables Annotation of Kidney Genome-Wide Association Study Loci Karsten B. Sieber,1 Anna Batorsky,2 Kyle Siebenthall,2 Kelly L. Hudkins,3 Jeff D. Vierstra,2 Shawn Sullivan,4 Aakash Sur,4,5 Michelle McNulty,6 Richard Sandstrom,2 Alex Reynolds,2 Daniel Bates,2 Morgan Diegel,2 Douglass Dunn,2 Jemma Nelson,2 Michael Buckley,2 Rajinder Kaul,2 Matthew G. Sampson,6 Jonathan Himmelfarb,7,8 Charles E. Alpers,3,8 Dawn Waterworth,1 and Shreeram Akilesh3,8 Due to the number of contributing authors, the affiliations are listed at the end of this article. ABSTRACT Background Linking genetic risk loci identified by genome-wide association studies (GWAS) to their causal genes remains a major challenge. Disease-associated genetic variants are concentrated in regions con- taining regulatory DNA elements, such as promoters and enhancers. Although researchers have previ- ously published DNA maps of these regulatory regions for kidney tubule cells and glomerular endothelial cells, maps for podocytes and mesangial cells have not been available. Methods We generated regulatory DNA maps (DNase-seq) and paired gene expression profiles (RNA-seq) from primary outgrowth cultures of human glomeruli that were composed mainly of podo- cytes and mesangial cells. We generated similar datasets from renal cortex cultures, to compare with those of the glomerular cultures. Because regulatory DNA elements can act on target genes across large genomic distances, we also generated a chromatin conformation map from freshly isolated human glomeruli. Results We identified thousands of unique regulatory DNA elements, many located close to transcription factor genes, which the glomerular and cortex samples expressed at different levels. -

High-Resolution Characterization of the Leukemic Cutaneous T-Cell Lymphoma Genome William Lin
Yale University EliScholar – A Digital Platform for Scholarly Publishing at Yale Yale Medicine Thesis Digital Library School of Medicine January 2011 High-Resolution Characterization Of The Leukemic Cutaneous T-Cell Lymphoma Genome William Lin Follow this and additional works at: http://elischolar.library.yale.edu/ymtdl Recommended Citation Lin, William, "High-Resolution Characterization Of The Leukemic Cutaneous T-Cell Lymphoma Genome" (2011). Yale Medicine Thesis Digital Library. 1573. http://elischolar.library.yale.edu/ymtdl/1573 This Open Access Thesis is brought to you for free and open access by the School of Medicine at EliScholar – A Digital Platform for Scholarly Publishing at Yale. It has been accepted for inclusion in Yale Medicine Thesis Digital Library by an authorized administrator of EliScholar – A Digital Platform for Scholarly Publishing at Yale. For more information, please contact [email protected]. Lin et al. Yale University School of Medicine Thesis High-resolution characterization of the leukemic cutaneous T cell lymphoma genome A Thesis Submitted to the Yale University School of Medicine in Partial Fulfillment of the Requirements for the Degree of Doctor of Medicine by William Michael Lin 2011 1 Lin et al. Yale University School of Medicine Thesis ACKNOWLEDGMENTS This study was supported by the following grants and awards: 1) Argall and Anna Hull Cancer Research Award from the Yale Cancer Center 2) Skin Cancer Foundation Research Grant 3) American Skin Association Medical Student Award 4) Etta S. Chidsey Award in Cancer Research 5) Yale School of Medicine Student Fellowship. 6) This study was also supported in part by research funding from Affymetrix, Inc. -

Supplementary Tables
Supplementary Tables Supplementary Table 1. Differentially methylated genes in correlation with their expression pattern in the A4 progression model A. Hypomethylated–upregulated Genes (n= 76) ALOX5 RRAD RTN4R DSCR6 FGFR3 HTR7 WNT3A POGK PLCD3 ALPPL2 RTEL1 SEMA3B DUSP5 FOSB ITGB4 MEST PPL PSMB8 ARHGEF4 BST2 SEMA7A SLC12A7 FOXQ1 KCTD12 LETM2 PRPH PXMP2 ARNTL2 CDH3 SHC2 SLC20A2 HSPA2 KIAA0182 LIMK2 NAB1 RASIP1 ASRGL1 CLDN3 DCBLD1 SNX10 SSH1 KREMEN2 LIPE NDRG2 ATF3 CLU DCHS1 SOD3 ST3GAL4 MAL LRRC1 NR3C2 ATP8B3 CYC1 DGCR8 EBAG9 SYNGR1 TYMS MCM2 NRG2 RHOF DAGLA DISP2 FAM19A5 TNNI3 UNC5B MYB PAK6 RIPK4 DAZAP1 DOCK3 FBXO6 HSPA4L WHSC1 PNMT PCDH1 B. Hypermethylated-downregulated Genes (n= 31) ARHGAP22 TNFSF9 KLF6 LRP8 NRP1 PAPSS2 SLC43A2 TBC1D16 ASB2 DZIP1 TPM1 MDGA1 NRP2 PIK3CD SMARCA2 TLL2 C18orf1 FBN1 LHFPL2 TRIO NTNG2 PTGIS SOCS2 TNFAIP8 DIXDC1 KIFC3 LMO1 NR3C1 ODZ3 PTPRM SYNPO Supplementary Table 2. Genes enriched for different histone methylation marks in A4 progression model identified through ChIP-on-chip a. H3K4me3 (n= 978) AATF C20orf149 CUL3 FOXP1 KATNA1 NEGR1 RAN SPIN2B ABCA7 C20orf52 CWF19L1 FRK KBTBD10 NEIL1 RANBP2 SPPL2A ABCC9 C21orf13-SH3BGR CXCL3 FSIP1 KBTBD6 NELF RAPGEF3 SPRY4 ABCG2 C21orf45 CYC1 FUK KCMF1 NFKB2 RARB SPRYD3 ABHD7 C22orf32 CYorf15A FXR2 KCNH7 NGDN RASAL2 SPTLC2 ACA15 C2orf18 DAXX FZD9 KCNMB4 NKAP RASD1 SRFBP1 ACA26 C2orf29 DAZ3 G6PD KCTD18 NKTR RASEF SRI ACA3 C2orf32 DBF4 GABPB2 KDELR2 NNT RASGRF1 SRM ACA48 C2orf55 DBF4B GABRA5 KIAA0100 NOL5A RASSF1 SSH2 ACAT1 C3orf44 DBI GADD45B KIAA0226 NOLC1 RASSF3 SSH3 ACSL5 -

Whole-Exome Sequencing Validates a Preclinical Mouse Model for the Prevention and Treatment of Cutaneous Squamous Cell Carcinoma Elena V
Published OnlineFirst December 6, 2016; DOI: 10.1158/1940-6207.CAPR-16-0218 Research Article Cancer Prevention Research Whole-Exome Sequencing Validates a Preclinical Mouse Model for the Prevention and Treatment of Cutaneous Squamous Cell Carcinoma Elena V. Knatko1, Brandon Praslicka2, Maureen Higgins1, Alan Evans3, Karin J. Purdie4, Catherine A. Harwood4, Charlotte M. Proby1, Aikseng Ooi2, and Albena T. Dinkova-Kostova1,5,6 Abstract Cutaneous squamous cell carcinomas (cSCC) are among the detected in 15 of 18 (83%) cases, with 20 of 21 SNP mutations most common and highly mutated human malignancies. Solar located in the protein DNA-binding domain. Strikingly, multiple UV radiation is the major factor in the etiology of cSCC. Whole- nonsynonymous SNP mutations in genes encoding Notch family exome sequencing of 18 microdissected tumor samples (cases) members (Notch1-4) were present in 10 of 18 (55%) cases. The derived from SKH-1 hairless mice that had been chronically histopathologic spectrum of the mouse cSCC that develops in this exposed to solar-simulated UV (SSUV) radiation showed a medi- model resembles very closely the spectrum of human cSCC. We an point mutation (SNP) rate of 155 per Mb. The majority conclude that the mouse SSUV cSCCs accurately represent the (78.6%) of the SNPs are C.G>T.A transitions, a characteristic histopathologic and mutational spectra of the most prevalent UVR-induced mutational signature. Direct comparison with tumor suppressors of human cSCC, validating the use of this human cSCC cases showed high overlap in terms of both fre- preclinical model for the prevention and treatment of human quency and type of SNP mutations. -
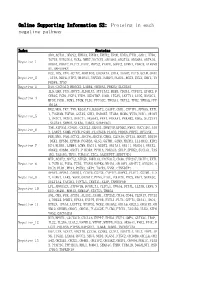
Online Supporting Information S2: Proteins in Each Negative Pathway
Online Supporting Information S2: Proteins in each negative pathway Index Proteins ADO,ACTA1,DEGS2,EPHA3,EPHB4,EPHX2,EPOR,EREG,FTH1,GAD1,HTR6, IGF1R,KIR2DL4,NCR3,NME7,NOTCH1,OR10S1,OR2T33,OR56B4,OR7A10, Negative_1 OR8G1,PDGFC,PLCZ1,PROC,PRPS2,PTAFR,SGPP2,STMN1,VDAC3,ATP6V0 A1,MAPKAPK2 DCC,IDS,VTN,ACTN2,AKR1B10,CACNA1A,CHIA,DAAM2,FUT5,GCLM,GNAZ Negative_2 ,ITPA,NEU4,NTF3,OR10A3,PAPSS1,PARD3,PLOD1,RGS3,SCLY,SHC1,TN FRSF4,TP53 Negative_3 DAO,CACNA1D,HMGCS2,LAMB4,OR56A3,PRKCQ,SLC25A5 IL5,LHB,PGD,ADCY3,ALDH1A3,ATP13A2,BUB3,CD244,CYFIP2,EPHX2,F CER1G,FGD1,FGF4,FZD9,HSD17B7,IL6R,ITGAV,LEFTY1,LIPG,MAN1C1, Negative_4 MPDZ,PGM1,PGM3,PIGM,PLD1,PPP3CC,TBXAS1,TKTL2,TPH2,YWHAQ,PPP 1R12A HK2,MOS,TKT,TNN,B3GALT4,B3GAT3,CASP7,CDH1,CYFIP1,EFNA5,EXTL 1,FCGR3B,FGF20,GSTA5,GUK1,HSD3B7,ITGB4,MCM6,MYH3,NOD1,OR10H Negative_5 1,OR1C1,OR1E1,OR4C11,OR56A3,PPA1,PRKAA1,PRKAB2,RDH5,SLC27A1 ,SLC2A4,SMPD2,STK36,THBS1,SERPINC1 TNR,ATP5A1,CNGB1,CX3CL1,DEGS1,DNMT3B,EFNB2,FMO2,GUCY1B3,JAG Negative_6 2,LARS2,NUMB,PCCB,PGAM1,PLA2G1B,PLOD2,PRDX6,PRPS1,RFXANK FER,MVD,PAH,ACTC1,ADCY4,ADCY8,CBR3,CLDN16,CPT1A,DDOST,DDX56 ,DKK1,EFNB1,EPHA8,FCGR3A,GLS2,GSTM1,GZMB,HADHA,IL13RA2,KIR2 Negative_7 DS4,KLRK1,LAMB4,LGMN,MAGI1,NUDT2,OR13A1,OR1I1,OR4D11,OR4X2, OR6K2,OR8B4,OXCT1,PIK3R4,PPM1A,PRKAG3,SELP,SPHK2,SUCLG1,TAS 1R2,TAS1R3,THY1,TUBA1C,ZIC2,AASDHPPT,SERPIND1 MTR,ACAT2,ADCY2,ATP5D,BMPR1A,CACNA1E,CD38,CYP2A7,DDIT4,EXTL Negative_8 1,FCER1G,FGD3,FZD5,ITGAM,MAPK8,NR4A1,OR10V1,OR4F17,OR52D1,O R8J3,PLD1,PPA1,PSEN2,SKP1,TACR3,VNN1,CTNNBIP1 APAF1,APOA1,CARD11,CCDC6,CSF3R,CYP4F2,DAPK1,FLOT1,GSTM1,IL2 -

Identifying Drug Sensitivity Subnetworks with NETPHIX
bioRxiv preprint doi: https://doi.org/10.1101/543876. this version posted February 8, 2019. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. It is made available under a CC-BY-NC-ND 4.0 International license. Identifying Drug Sensitivity Subnetworks with NETPHLIX Yoo-Ah Kim *† Rebecca Sarto Basso *†‡ Damian Wojtowicz † Dorit S. Hochbaum ‡ Fabio Vandin §¶ Teresa M. Prztycka †¶ Abstract Phenotypic heterogeneity in cancer is often caused by different patterns of genetic alterations. Under- standing such phenotype-genotype relationships is fundamental for the advance of personalized medicine. One of the important challenges in the area is to predict drug response on a personalized level. The pathway- centric view of cancer significantly advanced the understanding of genotype-phenotype relationships. How- ever, most of network identification methods in cancer focus on identifying subnetworks that include gen- eral cancer drivers or are associated with discrete features such as cancer subtypes, hence cannot be applied directly for the analysis of continuous features like drug response. On the other hand, existing genome wide association approaches do not fully utilize the complex proprieties of cancer mutational landscape. To ad- dress these challenges, we propose a computational method, named NETPHLIX (NETwork-to-PHenotpe mapping LeveragIng eXlusivity), which aims to identify mutated subnetworks that are associated with drug response (or any continuous cancer phenotype). Utilizing properties such as mutual exclusivity and interac- tions among genes, we formulate the problem as an integer linear program and solve it optimally to obtain a set of genes satisfying the constraints. NETPHLIX identified gene modules significantly associated with many drugs, including interesting response modules to MEK1/2 inhibitors in both directions (increased and decreased sensitivity to the drug) that the previous method, which does not utilize network informa- tion, failed to identify.