Table of Contents 1
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Content Moderation Help Card
Content Moderation Help Card Content Moderation Content Moderation allows you to approve or decline content before it is posted to your website. Click Content Moderation and select Moderated Groups to begin the setup process. You can configure Content Moderation two ways. 1. Choose workspaces that are always moderated (e.g., sections, site homepages). Content added to workspaces specified in a Content Group will require approval for all editors when you activate the Moderate All Editors checkbox for the Content Group. 2. Set combinations of workspaces and editors requiring moderation (e.g., the PTO section and user Eric Sparks). Creating Content Groups Adding Moderated Users You use Content Groups to define workspaces subject to Content Moderation. If you only wish to moderate some editors, you will need to add them as To create a Content Group... Moderated Users. Whenever a moderated user edits content in a workspace 1. In Site Manager, select Content Moderation from the Content Browser. specified in any of the Content Groups, that user will only be able to send 2. Select Moderated Groups. content for approval. 3. On the Content Groups tab, click New Content To add Moderated Users... Group. 1. In the Moderated Groups workspace, click Moderated Users. 4. Add a Name and a Description for your group and click 2. Click Add Group or Add User. Save. 3. Use Search to locate groups or users you wish to moderate. You can To add workspaces and moderators... filter groups by category. 1. Click on the name of your Content Group. 4. Click Select to the right of each group or user name. -

Eclipse Project Briefing Materials
[________________________] Eclipse project briefing materials. Copyright (c) 2002, 2003 IBM Corporation and others. All rights reserved. This content is made available to you by Eclipse.org under the terms and conditions of the Common Public License Version 1.0 ("CPL"), a copy of which is available at http://www.eclipse.org/legal/cpl-v10.html The most up-to-date briefing materials on the Eclipse project are found on the eclipse.org website at http://eclipse.org/eclipse/ 200303331 1 EclipseEclipse ProjectProject 200303331 3 Eclipse Project Aims ■ Provide open platform for application development tools – Run on a wide range of operating systems – GUI and non-GUI ■ Language-neutral – Permit unrestricted content types – HTML, Java, C, JSP, EJB, XML, GIF, … ■ Facilitate seamless tool integration – At UI and deeper – Add new tools to existing installed products ■ Attract community of tool developers – Including independent software vendors (ISVs) – Capitalize on popularity of Java for writing tools 200303331 4 Eclipse Overview Another Eclipse Platform Tool Java Workbench Help Development Tools JFace (JDT) SWT Team Your Tool Plug-in Workspace Development Debug Environment (PDE) Their Platform Runtime Tool Eclipse Project 200303331 5 Eclipse Origins ■ Eclipse created by OTI and IBM teams responsible for IDE products – IBM VisualAge/Smalltalk (Smalltalk IDE) – IBM VisualAge/Java (Java IDE) – IBM VisualAge/Micro Edition (Java IDE) ■ Initially staffed with 40 full-time developers ■ Geographically dispersed development teams – OTI Ottawa, OTI Minneapolis, -

1400.0 Nrcs Minnesota Workspaces And
NRCS MINNESOTA WORKSPACES AND CUSTOMIZATION 1400.0 The Civil 3D software utilizes workspaces to control the display of the work area, including drop-down menus, placement of toolbars and commands included in toolbars. Available Workspaces are selected from the drop-down list on the Workspaces toolbar. Several standard workspaces will be provided when the program is installed, and the procedure for configuring customized workspaces is covered below. 1. Customizing workspaces a. To make changes to a workspace, select the Customize command from the drop-down menu on the workspaces toolbar. b. This will bring up the Customize User Interface window. Selecting a workspace from the available list in the top left hand pane will display all of the setting that can be modified in the Workspace Contents pane in the upper right hand side of the window. A listing of all of the available commands is included in the lower left hand pane. Click on the Customize Workspace button in the Workspace Contents pane to begin modifying the selected workspace. Civil 3D 2012 1 Rev. 1/2013 1400.0 WORKSPACES AND CUSTOMIZATION NRCS MINNESOTA 2. Partial customization files a. Additional customization files can be loaded as partial customization files, which gives you access to additional commands and menus. You can add partial customization files by clicking on the Load partial customization file icon next to the customization file drop-down list. This icon will be inactivated if you are in the process of customizing a workspace, so you will need to click on the Done button in the Workspace Contents frame (see above) to exit the customization mode before you can load a partial customization file. -

Workspace Desktop Edition
Workspace Desktop Edition 8.5.124.08 9/27/2021 8.5.124.08 8.5.124.08 Workspace Desktop Edition Release Notes Release Date Release Type Restrictions AIX Linux Solaris Windows 02/28/18 Update X Contents • 1 8.5.124.08 • 1.1 Helpful Links • 1.2 What's New • 1.3 Resolved Issues • 1.4 Upgrade Notes Workspace Desktop Edition 2 8.5.124.08 What's New Helpful Links This release contains the following new features and enhancements: Releases Info • The rich text email editor Font menu now displays the full list of fonts • List of 8.5.x Releases available on the agent workstation. Previously, only one font per font family was displayed. • 8.5.x Known Issues • Screen Reader applications can now read the names of colors inside the email Rich Text Editor color Picker control. • Agents can now press the Enter key to insert a selected standard Product Documentation response into an email, chat, or other text-based interaction. Workspace Desktop Edition • It is now possible to sort the content of an 'auto-update' workbin based on a column containing integer values. For that purpose, the key-value pair 'interaction-workspace/display-type'='int' must be specified in the annex of Genesys Products the Business Attribute Value corresponding to that column in the Business Attribute "Interaction Custom Properties". Previously those columns were List of Release Notes sorted as strings. • On an Alcatel 4400 / OXE switch, a Supervisor can now fully log out of the voice channel when exiting Workspace if the value of the logout.voice.use-login-queue-on-logout option is set to true. -

Citrix Workspace
Citrix Workspace Citrix Product Documentation | docs.citrix.com July 13, 2020 Citrix Workspace Contents Citrix Workspace 3 What’s New 6 Get Started with Citrix Workspace 7 Citrix Workspace app and Citrix Receiver 11 Configure workspaces 16 Aggregate on-premises virtual apps and desktops in workspaces 36 Enable single sign-on for workspaces with Citrix Federated Authentication Service 46 Optimize connectivity to workspaces with Direct Workload Connection 57 Secure workspaces 66 Manage your workspace experience 73 Citrix Assistant 80 © 1999-2020 Citrix Systems, Inc. All rights reserved. 2 Citrix Workspace Citrix Workspace May 28, 2020 Citrix Workspace is a complete digital workspace solution that allows you to deliver secure access to the information, apps, and other content that are relevant to a person’s role in your organization. Users subscribe to the services you make available and can access them from anywhere, on any de- vice. Citrix Workspace helps you organize and automate the most important details your users need to collaborate, make better decisions, and focus fully on their work. For a complete description of each Citrix Workspace edition and included features, see the Citrix Workspace Feature Matrix. Get started Citrix Workspace includes a step-by-step walkthrough to help you deliver workspaces quickly. Each step guides you through the Citrix Cloud console with simple instructions for tasks like configuring your identity provider, selecting your workspace authentication, and enabling the other services that come with Workspace. The walkthrough also provides quick access to the technical information you’ll need when you’re assembling your deployment team and configuring your infrastructure and resources. -

Get to Know Grants.Gov Workspace
GET TO KNOW GRANTS.GOV WORKSPACE This guide provides an overview and some tips for using Grants.gov Workspace. It is not intended to be a step-by- step walkthrough that covers all aspects of submitting an application. Though switching from Coeus to agency systems marks a new business process for JHU, Workspace is not a new system. Once you’ve logged it to check Workspace out yourself, you’ll be surprised by how familiar the forms are and how intuitive the system is. In this guide, “Workspace” refers to the system and “workspace” refers to your workspace application. If have questions and want to learn more, we’ve added a list of resources and a FAQ to the end of this document. OVERVIEW GENERAL • Only use for Workspace for submissions to agencies that do not have a dedicated submission portal (e.g. CDC, HRSA, DOD, etc.) • Files cannot exceed 200MB. • Do not use the Adobe attachment function (the paper clip in the taskbar) to upload files. You must use the in-form “Add Attachment” option. Not using the in-form options will cause errors. • Disable pop-up blockers for the Grants.gov site. Some confirmation boxes appear in pop- up windows. • Available and required forms vary by FOA and agency. Always read the application instructions carefully. • Like the Adobe Legacy forms, completing the SF424 R&R form will populate some fields in the rest of the package. ACCESS AND OWNERSHIP • You can only create a workspace if you have a Grants.gov account with the “Manage Workspace” role. • The person who creates the workspace is workspace owner and can grant other users access to the workspace. -

CSC245 - Web Technologies and Programming Homework Assignment 5: Baby Names
CSC245 - Web Technologies and Programming Homework Assignment 5: Baby Names This assignment tests your understanding of fetching data from files and web services using Ajax requests. You must match in appearance and behavior the following web page: Background Information: Every 10 years, the Social Security Administration provides data about the 1000 most popular boy and girl names for children born in the US, at http://www.ssa.gov/OACT/babynames/ . Your task for this assignment is to write the JavaScript code for a web page to display the baby names, popularity rankings, and meanings. You do not need to submit any HTML or CSS file. You will be provided with the HTML (names.html) and CSS (names.css) code to use. Turn in only the following file: ◦ names.Js, the JavaScript code for your Baby Names web page Data: Your program will get its data from a web service located at the following URL: https://cs.berry.edu/webdev/scripts/labs/babynames/babynames.php This web service has three “modes,” each of which provides a different type of data. Specify which type of data you want from it by changing a query parameter named type. Each query returns either plain text or JSON as its output. If you make a malformed request, such as one missing a necessary parameter, the service will respond with an HTTP error code of 400 rather than the default 200. If you request data for a name the server doesn't have data for, the service will respond with an error code of 404. (Hint: You can test queries by typing the URL of the web service, along with the appropriate query string parameters, in your web browser's address bar and seeing the result. -

Getting Started with Workspace
Mobi Setup Install the Software Check to see if the software has been loaded on the computer: o Go to Start > Programs > eInstruction > Interwrite Workspace If the software is not loaded, you or your lab assistant can install the software (use the provided CD) DO NOT connect the Bluetooth receiver before installing the software Note: At least once a semester, be sure to click the Interwrite icon in the bottom taskbar and select “check for updates” Connect the Mobi 1. Insert the hub into the USB port on the computer. The blue LED will light up on the hub when plugged in. 2. Press the lighted activation button on the hub. The light should start blinking. 3. Turn on the Mobi. 4. Turn the Mobi over and press the blue button next to the battery opening to activate the Mobi’s signal. NOTE: This is a one time set up – future connects will be automatic. When not in use, store the hub in the storage area on the back of the Mobi. Charge the Mobi Make sure pen is secure and plug the Mobi tablet into the docking station Battery icon indicates charging status Full charge is 12 hours Mobi Status Indicators Parts of the Mobi Workspace Software Launch Workspace 1. Go to Start > Programs > eInstruction > Interwrite Workspace - a blank screen will appear. 2. From the toolbar, select blank page. Four Parts of Workspace I. Main Toolbar (right) – (defaults to Intermediate toolbar) o To Change the Toolbar Button Shape and Size 1. Click the down arrow on the toolbar and choose Preferences. -

Navigation Patterns and Usability of Zoomable User Interfaces with and Without an Overview
Navigation Patterns and Usability of Zoomable User Interfaces with and without an Overview KASPER HORNBÆK University of Copenhagen and BENJAMIN B. BEDERSON and CATHERINE PLAISANT University of Maryland The literature on information visualization establishes the usability of interfaces with an overview of the information space, but for zoomable user interfaces, results are mixed. We compare zoomable user interfaces with and without an overview to understand the navigation patterns and usability of these interfaces. Thirty-two subjects solved navigation and browsing tasks on two maps. We found no difference between interfaces in subjects’ ability to solve tasks correctly. Eighty percent of the subjects preferred the interface with an overview, stating that it supported navigation and helped keep track of their position on the map. However, subjects were faster with the interface without an overview when using one of the two maps. We conjecture that this difference was due to the organization of that map in multiple levels, which rendered the overview unnecessary by providing richer navigation cues through semantic zooming. The combination of that map and the interface without an overview also improved subjects’ recall of objects on the map. Subjects who switched between the overview and the detail windows used more time, suggesting that integration of overview and detail windows adds complexity and requires additional mental and motor effort. Categories and Subject Descriptors: H.5.2 [Information Interfaces and Presentation]: User Interfaces—evaluation/methodology; interaction styles (e.g., commands, menus, forms, direct ma- nipulation); I.3.6 [Computer Graphics]: Methodology and Techniques—interaction techniques General Terms: Experimentation, Human Factors, Measurement, Performance Additional Key Words and Phrases: Information visualization, zoomable user interfaces (ZUIs), overviews, overview+detail interfaces, navigation, usability, maps, levels of detail 1. -
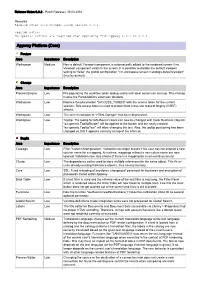
Appway 6.3.2 Release Notes
Release Notes 6.3.2 - Patch Release | 30.03.2016 Remarks Release notes with changes since version 6.3.1. Upgrade Notes: No special actions are required when upgrading from Appway 6.3.1 to 6.3.2. Appway Platform (Core) Feature Area Importance Description Workspace Medium Now a default Viewport component is automatically added to the rendered screen if no Viewport component exists in the screen. It is possible to disable the default viewport setting to "false" the global configuration "nm.workspace.screen.metatags.defaultviewport" (true by default). Change Area Importance Description Process Engine Low Pre-populating the workflow token lookup cache with local content on start-up. This change makes the PortalAddOns extension obsolete. Workspace Low Replace the placeholder "{ACCESS_TOKEN}" with the access token for the current session. This access token is used to protect from cross-site request forgery (CSRF) attacks. Workspace Low The screen component "HTML Doctype" has been deprecated. Workspace Low Tooltip: The tooltip for Info Boxes' colors can now be changed with Color Business Objects: "aw.generic.TooltipBorder" will be applied to the border and the newly created "aw.generic.TooltipText" will allow changing the text. Also, the tooltip positioning has been changed so that it appears correctly on top of the info icon. Bugfix Area Importance Description Catalogs Low Filter "Column Manipulation": Validation no longer breaks if the user has not entered a new column name for a mapping. At runtime, mappings without a new colum name are now ignored. Validation now also checks if there is a mapping for a non-existing column. -

IBM Cognos Workspace Version 10.2.2: User Guide Chapter 4
IBM Cognos Workspace Version 10.2.2 User Guide Note Before using this information and the product it supports, read the information in “Notices” on page 137. Product Information This document applies to IBM Cognos Business Intelligence Version 10.2.2 and may also apply to subsequent releases. Licensed Materials - Property of IBM © Copyright IBM Corporation 2010, 2014. US Government Users Restricted Rights – Use, duplication or disclosure restricted by GSA ADP Schedule Contract with IBM Corp. Contents Introduction ..................................ix Chapter 1. What's new in Cognos Workspace ...................1 New features in Cognos Workspace version 10.2.2 .......................1 Button filter widgets................................1 Specification of the orientation of filter widgets .......................1 Report widgets .................................2 Filters that are based on visualizations..........................2 New features in Cognos Workspace version 10.2.1.1 ......................2 Extensible visualizations ..............................2 Embedding and customizing workspaces .........................3 Cutting, copying, and pasting widgets and duplicating tabs ..................3 Support for IBM Cognos Theme Designer ........................3 Sort function in widgets is available for users with the Consume capability .............3 New features in Cognos Workspace version 10.2.1 .......................3 Filtering on multiple related data items in select value filter and slider filter widgets ..........4 Automatically -

Chapter 2. Graphical User Interface (GUI)
Chapter 2. Graphical User Interface (GUI) The FLUENT graphical interface consists of a menu bar to access the menus, a toolbar, a navigation pane, a task page, a graphics toolbar, graphics windows, and a console, which is a textual command line interface (described in Chapter 3: Text User Interface (TUI)). You will have access to the dialog boxes via the task page or the menus. • Section 2.1: GUI Components • Section 2.2: Customizing the Graphical User Interface (UNIX Systems Only) • Section 2.3: Using the GUI Help System 2.1 GUI Components The graphical user interface (GUI) is made up of seven main components: the menu bar, toolbars, a navigation pane, task pages, a console, dialog boxes, and graphics windows. When you use the GUI, you will be interacting with one of these components at all times. Figure 2.1.1 is a sample screen shot showing all of the GUI components. The seven GUI components are described in detail in the subsequent sections. On Linux/UNIX systems, the attributes of the GUI (including colors and text fonts) can be customized to better match your platform environment. This is described in Section 2.2: Customizing the Graphical User Interface (UNIX Systems Only). 2.1.1 The Menu Bar The menu bar organizes the GUI menu hierarchy using a set of pull-down menus. A pull-down menu contains items that perform commonly executed actions. Figure 2.1.2 shows the FLUENT menu bar. Menu items are arranged to correspond to the typical sequence of actions that you perform in ANSYS FLUENT (i.e., from left to right and from top to bottom).