Size Elasticity on Housing Rent of Informal Housing Market
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A/Tw/516 A-1
°Ñ¦Ò ø REFERENCE No. DRAWING A/TW/516 A-1 ¡]¨Ó·½¡ Ia¡ (Source : Appendix Ia) °Ñ¦Ò ø REFERENCE No. DRAWING A/TW/516 A-2 ¡]¨Ó·½¡ Ia¡ (Source : Appendix Ia) °Ñ¦Ò ø REFERENCE No. DRAWING A/TW/516 A-3 ¡]¨Ó·½¡ Ia¡ (Source : Appendix Ia) °Ñ¦Ò ø REFERENCE No. DRAWING A/TW/516 A-4 ¡]¨Ó·½¡ Ia¡ (Source : Appendix Ia) °Ñ¦Ò ø REFERENCE No. DRAWING A/TW/516 A-5 ¡]¨Ó·½¡ Ia¡ (Source : Appendix Ia) °Ñ¦Ò ø REFERENCE No. DRAWING A/TW/516 A-6 ¡]¨Ó·½¡ Ia¡ (Source : Appendix Ia) °Ñ¦Ò ø REFERENCE No. DRAWING A/TW/516 A-7 ¡]¨Ó·½¡ Ic¡ (Source : Appendix Ic) °Ñ¦Ò ø REFERENCE No. DRAWING A/TW/516 A-8 ¡]¨Ó·½¡ Ic¡ (Source : Appendix Ic) °Ñ¦Ò ø REFERENCE No. DRAWING A/TW/516 A-9 ¡]¨Ó·½¡ Ia¡ (Source : Appendix Ia) G/IC B R(A) G/IC(5) G GB V G/IC(8) 509 (13.12.19) 路口 (有待詳細設計) ROAD JUNCTION (SUBJECT TO DETAILED DESIGN) G/IC 508 (17.01.20) R(B)4 4 W an g L ung 514 (29.05.20) St ¥Ó½Ð ¹Ï LEGEND APPLICATION SITE Àò§å•ã ¥ý«e 505 (01.11.19) APPROVED APPLICATION PREVIOUS APPLICATION 505 (01.11.19) ³Q©Úµ´ 415 (05.08.11) 415 (05.08.11) REJECTED APPLICATION 505 (01.11.19) ·|ij DATE OF MEETING ¥Ó½Ð APPLICATION NUMBER ¹ê¦a·Ó¤ù 4 VIEWING POINT OF SITE OU PHOTO ¥Ó½Ð¦aÂI¬É½ APPLICATION SITE BOUNDARY R(A)8 美化市容地帶 FOR IDENTIFICATION PURPOSE ONLY AMENITY AREA ¦ì¸ LOCATION PLAN ³W¹ 擬議略為放寬地積比率限制 ¥»ºK•n¹Ï©ó2020¦~5¤ë29¤éÀ 以作准許的工業用途 ¬°©ó2017¦~4¤ë11¤é®Ö•ãªº¤ 荃灣灰窰角街24-32號 PLANNING DEPARTMENT S/TW/33 PROPOSED MINOR RELAXATION OF PLOT RATIO RESTRICTION EXTRACT PLAN PREPARED ON 29.5.2020 FOR PERMITTED INDUSTRIAL USE BASED ON OUTLINE ZONING PLAN No. -

New Territories
Branch ATM District Branch / ATM Address Voice Navigation ATM 1009 Kwai Chung Road, Kwai Chung, New Kwai Chung Road Branch P P Territories 7-11 Shek Yi Road, Sheung Kwai Chung, New Sheung Kwai Chung Branch P P P Territories 192-194 Hing Fong Road, Kwai Chung, New Ha Kwai Chung Branch P P P Territories Shop 102, G/F Commercial Centre No.1, Cheung Hong Estate Commercial Cheung Hong Estate, 12 Ching Hong Road, P P P P Centre Branch Tsing Yi, New Territories A18-20, G/F Kwai Chung Plaza, 7-11 Kwai Foo Kwai Chung Plaza Branch P P Road, Kwai Chung, New Territories Shop No. 114D, G/F, Cheung Fat Plaza, Cheung Fat Estate Branch P P P P Cheung Fat Estate, Tsing Yi, New Territories Shop 260-265, Metroplaza, 223 Hing Fong Metroplaza Branch P P Road, Kwai Chung, New Territories 40 Kwai Cheong Road, Kwai Chung, New Kwai Cheong Road Branch P P P P Territories Shop 115, Maritime Square, Tsing Yi Island, Maritime Square Branch P P New Territories Maritime Square Wealth Management Shop 309A-B, Level 3, Maritime Square, Tsing P P P Centre Yi, New Territories ATM No.1 at Open Space Opposite to Shop No.114, LG1, Multi-storey Commercial /Car Shek Yam Shopping Centre Park Accommodation(also known as Shek Yam Shopping Centre), Shek Yam Estate, 120 Lei Muk Road, Kwai Chung, New Territories. Shop No.202, 2/F, Cheung Hong Shopping Cheung Hong Estate Centre No.2, Cheung Hong Estate, 12 Ching P Hong Road, Tsing Yi, New Territories Shop No. -

LCQ15-Annex2 (2010)
Annex 2 Record of Train Service Delays of 8 Minutes or More from 01/01/2010 to 31/12/2010 Incident Railway Line Delay Incident Time Cause of Incidents / Findings of Investigation Remedial Action Taken Date Affected (min.) 3-Jan-10 8:25 PM Light Rail A Light Rail Vehicle (LRV) was withdrawn from service after it was hit by a New Territories taxi at the No injuries were reported. Light Rail service resumed at 8:59 p.m. after the site was cleared. 35 junction between Tai Fong Street and Tai Hing Bus Terminus egress. The left-hand-side of the LRV car body was damaged. 4-Jan-10 6:30 PM Light Rail A LRV was withdrawn from service after a pair of doors failed to close after platform duties at Tin Shui Investigation found a faulty door component which was immediately replaced. 12 Wai Stop. The concerned LRV was pushed away from the site. 8-Jan-10 7:32 AM Tsuen Wan Line A Central-bound train was withdrawn from service at Tsuen Wan Station because the left-hand-side Investigation found a coin was jammed in the doors. It was immediately removed. 8 driving cab door failed to close after platform duties. 8-Jan-10 8:42 AM Tung Chung Line A Tung Chung- bound train was delayed at Tsing Yi Station because a points failed to detect its position. Investigation found faulty components of points equipment which were immediately replaced. 20 The train had to work in Restricted Manual Mode at a speed not more than 22 kph to pass the affected area. -
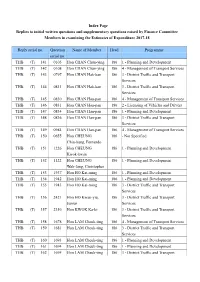
Index Page Replies to Initial Written Questions and Supplementary Questions Raised by Finance Committee Members in Examining the Estimates of Expenditure 2017-18
Index Page Replies to initial written questions and supplementary questions raised by Finance Committee Members in examining the Estimates of Expenditure 2017-18 Reply serial no. Question Name of Member Head Programme serial no. THB (T) 141 0105 Hon CHAN Chun-ying 186 1 - Planning and Development THB (T) 142 0108 Hon CHAN Chun-ying 186 4 - Management of Transport Services THB (T) 143 0797 Hon CHAN Hak-kan 186 3 - District Traffic and Transport Services THB (T) 144 0811 Hon CHAN Hak-kan 186 3 - District Traffic and Transport Services THB (T) 145 0830 Hon CHAN Han-pan 186 4 - Management of Transport Services THB (T) 146 0831 Hon CHAN Han-pan 186 2 - Licensing of Vehicles and Drivers THB (T) 147 0834 Hon CHAN Han-pan 186 1 - Planning and Development THB (T) 148 0836 Hon CHAN Han-pan 186 3 - District Traffic and Transport Services THB (T) 149 0984 Hon CHAN Han-pan 186 4 - Management of Transport Services THB (T) 150 0655 Hon CHEUNG 186 - Not Specified Chiu-hung, Fernando THB (T) 151 1226 Hon CHEUNG 186 1 - Planning and Development Kwok-kwan THB (T) 152 1122 Hon CHEUNG 186 1 - Planning and Development Wah-fung, Christopher THB (T) 153 1937 Hon HO Kai-ming 186 1 - Planning and Development THB (T) 154 1942 Hon HO Kai-ming 186 1 - Planning and Development THB (T) 155 1943 Hon HO Kai-ming 186 3 - District Traffic and Transport Services THB (T) 156 2421 Hon HO Kwan-yiu, 186 3 - District Traffic and Transport Junius Services THB (T) 157 2356 Hon KWOK Ka-ki 186 3 - District Traffic and Transport Services THB (T) 158 1678 Hon LAM Cheuk-ting 186 4 -

OFFICIAL RECORD of PROCEEDINGS Wednesday, 6
LEGISLATIVE COUNCIL ― 6 November 2019 1031 OFFICIAL RECORD OF PROCEEDINGS Wednesday, 6 November 2019 The Council met at Eleven o'clock MEMBERS PRESENT: THE PRESIDENT THE HONOURABLE ANDREW LEUNG KWAN-YUEN, G.B.S., J.P. THE HONOURABLE LEUNG YIU-CHUNG THE HONOURABLE ABRAHAM SHEK LAI-HIM, G.B.S., J.P. THE HONOURABLE TOMMY CHEUNG YU-YAN, G.B.S., J.P. PROF THE HONOURABLE JOSEPH LEE KOK-LONG, S.B.S., J.P. THE HONOURABLE JEFFREY LAM KIN-FUNG, G.B.S., J.P. THE HONOURABLE WONG TING-KWONG, G.B.S., J.P. THE HONOURABLE STARRY LEE WAI-KING, S.B.S., J.P. THE HONOURABLE CHAN HAK-KAN, B.B.S., J.P. THE HONOURABLE CHAN KIN-POR, G.B.S., J.P. DR THE HONOURABLE PRISCILLA LEUNG MEI-FUN, S.B.S., J.P. THE HONOURABLE WONG KWOK-KIN, S.B.S., J.P. THE HONOURABLE MRS REGINA IP LAU SUK-YEE, G.B.S., J.P. 1032 LEGISLATIVE COUNCIL ― 6 November 2019 THE HONOURABLE PAUL TSE WAI-CHUN, J.P. THE HONOURABLE CLAUDIA MO THE HONOURABLE MICHAEL TIEN PUK-SUN, B.B.S., J.P. THE HONOURABLE STEVEN HO CHUN-YIN, B.B.S. THE HONOURABLE FRANKIE YICK CHI-MING, S.B.S., J.P. THE HONOURABLE WU CHI-WAI, M.H. THE HONOURABLE YIU SI-WING, B.B.S. THE HONOURABLE MA FUNG-KWOK, S.B.S., J.P. THE HONOURABLE CHARLES PETER MOK, J.P. THE HONOURABLE CHAN CHI-CHUEN THE HONOURABLE CHAN HAN-PAN, B.B.S., J.P. THE HONOURABLE LEUNG CHE-CHEUNG, S.B.S., M.H., J.P. -

Annual Report for Session 2020/2021
Attachment 2 Annual Report for Session 2020/2021 1. Chairlady’s Statement It is my great honour to be the first Chairlady of the Division. With the Covid-19 pandemic bringing massive challenges to learned society activities, we have expedited all our efforts to keep up the continuous professional development for our members through application of the latest technologies. With the unconditional support of my fellow committee members, we have made our mission “Adapt to challenges and innovate to thrive for a sustainable future!” come true. Virtual Site Visits – Due to the pandemic it is almost impossible to arrange any physical site visits for our members, but with application of the latest technologies, we have successfully arranged more than 3 virtual site visits, each attracting more than 500 participants. I would like to take this opportunity to send my appreciation to all our partners who have worked together with us to achieve this successful milestone. Geotechnical Pioneer – Following on with the vision from the last Session, our “Geotechnical Pioneer” group has made a constant effort to arrange online workshops for our young engineers. After a year, we have finally completed the whole series of workshops on various geotechnical subjects that are commonly covered in the Professional Assessments for MHKIE(G). We will review the arrangement and re-run the workshops in suitable timing. Technical Competent Person (TCP) grade T3 Online Course and Examination – Following the arrangement from the last Session, we were once again able to obtain approval from the Buildings Department (BD) for arranging the TCP grade T3 top-up course using e-LMS and online exam. -

Xian Lu Green Tea Is Available at Wellcome Supermarket
Xian Lu green tea is available at Wellcome supermarket: District Location Tel Shop Address Hong Kong CENTRAL 25291357 Basement, Wah Kwong Regent Centre, Central, HK WAH FU ESTATE 25506795 Town Centre 2 at Level 120, 140 Wah Fu Estate, HK WESTWOOD 25427174 3/F The Westwood, 8 Belcher's Street, HK VICTORIA ROAD 28172502 Shop 3-7, Block 2, Centenary Mansion, 1 Victoria Road, Kennedy Town, HK CHONG YIP 21102067 Shop No. G21-G43 Ground Floor, Chong Yip Centre,402 – 404 Des Voeux Road West, HK BELCHER'S STREET 28185277 G/F, Lungga Mansion, 46A Belcher's Street, HK WATFORD ROAD 28497576 1/F, 2-4 Watford Road, The Peak, HK MAY ROAD 2530 9876 UG/F, Clovelly Court, 12 May Road, Peak, HK SEYMOUR TERRACE 25171036 LG/F & G/F, 1 Seymour Terrace, Mid-levels, HK CITY GARDEN 3580 7319 G/F Commerial Podiums Below Block , 7-14 City Garden , No. 233 Electrial Road , H.K TIN HAU TEMPLE ROAD 28071456 Shop A, G/F, Magnolia Mansion, 4 Tin Hau Temple Road, HK CAUSEWAY BAY 25773215 25-29 Great George Street, Causeway Bay, HK WAN CHAI 28930215 Basement, 194-204, Johnston Road, HK JAFFE ROAD 25746437 Portion of G/F, 503-505, Jaffe Road, Causeway Bay, HK LUCKY CENTRE 3188 4047 The Basement of Lucky Centre, 165-167 Wan Chai Road, HK HENNESSY ROAD 28382145 Basement (portion), 418-428 Hennessy Road, Wanchai, HK JOHNSTON ROAD 21104454 Basement & G/F Portion, Everwin Mansion, No. 18 Johnston Road, HK TAI KOO SHING 28853230 Shop G501, G/F, On Shing Terrace (Stage V), Tai Koo Shing, Tai Yue Avenue, HK RITZ GARDEN 2811 0478 Shop E, Basement, King's View Court, 901-907 King's Road, Quarry Bay, HK KORNHILL 2885 0337 Shop 1, G/F, 18 Hong Shing Street, Kornhill, HK METROPOLE SUPERSTORE 2564 0803 Portion of Basement, Metropole Building, No. -

Circle K Convenience Stores
Address(English) Kowloon Shop 3C, G/F., Fu Shun Hse, Fu Shan Est, Kln. Kowloon Shop no. 27-30, G/F., Amoy Plaza Phase 1, Ngau Tau Kok Rd, Kln. Kowloon Shop No. L110, Lok Fu Plaza, Wang Tau Hom, Kowloon Kowloon Shop 105, Tsui Lam Shopping Ctr, Tsui Lam Est, Tseung Kwan O, Kln. Kowloon Shop 110-112, Po Kan Hse, Po Lam Est, Tsueng Kwan O, Kln. Kowloon Shop 1, G/F., Carpark Bldg., Yan Ming Court Tseung Kwan O, Kln. Kowloon Shop 6, Tsui Ping Shopping Circuit, Kwun Tong, Kln. Kowloon Shop 3 & 4, Ka Yee Lau, Ka Wai Chuen, Hung Hom, Kln. Kowloon Shop 11, Chuk Yuen Shopping Ctr, Chuk Yuen Est, Kln. Kowloon G/F., Cheong Shing Court, 669 Gillies Rd, Tokwawan, Hunghom, Kln. Kowloon G/F., Kam Pik Hse, Choi Hung Est, Kwun Tong, Kln. Kowloon G/F., Nam Shan Est Comm. Bldg., Nam Shan Est, Shek Kip Mei, Kln. Kowloon Shop 101, Lung Poon Court Comm. Ctr, Lung Poon Court, Wong Tai Sin, Kln. Kowloon Shop 43 & 44, G/F., Hunghom Comm. Square, 37-39 Ma Tau Wai Rd., Hung Hom, Kln. Kowloon Shop 1, Carpark Bldg., Ko Chun Court, Yau Tong, Kln. Kowloon G/F., 273 Tokwawan Rd, Tokwawan, Kln. Kowloon Shop 1 Tsz Ching Shopping, Centre 1 Tsz Ching Est., Kln. Kowloon Shop no. 19, Ming Tak Shopping Ctr, Ming Tak Est, Tseung Kwan O, Kln. Kowloon Shop no. 8, G/F., Sheung Tak Shopping Centre, Tseung Kwan O, Kowloon. Kowloon G/F., Li Fung Tower, No. 868 Cheung Sha Wan Road, Kowloon. -

GN 7023 Roads
G.N. 7023 Roads (Works, Use and Compensation) Ordinance (Chapter 370) (Notice under section 8(2)) PWP ITEM NO. 6190TB PROPOSED RETROFITTING OF ESCALATORS FOR FOOTBRIDGE ACROSS CASTLE PEAK ROAD—KWAI CHUNG NEAR MTR TAI WO HAU STATION EXIT B Notice is hereby given that under powers delegated by the Secretary for Transport and Housing under section 3(3) of the Roads (Works, Use and Compensation) Ordinance (Chapter 370), the Permanent Secretary for Transport and Housing (Transport) proposes to execute the road works within the limit of works area as shown on Plan No. HWDKS145B-GZ0001 (‘the Plan’) and described in the scheme annexed thereto, which the Plan and scheme have been deposited in the Land Registry. The general nature of the proposed works is as follows:— (i) construction of covered two-way escalators of approximately 1 metre (m) in clear width at the existing footbridge No. NF77 across Castle Peak Road—Kwai Chung near MTR Tai Wo Hau Station Exit B; (ii) construction of covered staircase, walkway cover and footpath; (iii) permanent closure and conversion of sections of the existing footpath into the proposed covered two-way escalators in (i), the proposed covered staircase in (ii) and amenity area; (iv) permanent closure and conversion of sections of the existing amenity areas into the proposed covered two-way escalators in (i), the proposed covered staircase in (ii) and footpath; (v) permanent closure and demolition of the existing covered staircase; (vi) demolition of a section of the existing walkway cover; (vii) temporary closure of sections of the existing carriageway, footpath, footbridge and amenity areas; and (viii) ancillary works including drainage, utilities, landscaping, public lighting and electrical and mechanical works, as well as installation of street furniture and traffic aids. -

Tsuen Wan East
- 1 - CAVERN MASTER PLAN – INFORMATION NOTE STRATEGIC CAVERN AREA NO. 15 – TSUEN WAN EAST This Information Note describes the characteristics, key development opportunities and constraints of Strategic Cavern Area No. 15 - Tsuen Wan East (the SCVA). It indicates the potential land uses suitable for cavern development within the area, but would not pre-empt other possible land uses put forward by the project proponents with justifications. It also denotes the extent of potential portal locations. The spatial context of the SCVA is illustrated in the Reference Drawing appended to this Information Note. Reference should be made to the Explanatory Statement of the Cavern Master Plan for its background and purposes, as well as the definition and delineation criteria of SCVAs. 1. Location Plan Information Note (SCVA15 – Tsuen Wan East) - 2 - 2. Strategic Cavern Area Details Outline Zoning Plan (OZP): Approved Tsuen Wan OZP No. S/TW/33 Area: 67.7 ha Maximum elevation in the SCVA: +440 mPD Minimum elevation in the SCVA: +103 mPD 3. District Context Location The SCVA is located at the northeastern part of Tsuen Wan, which is geographically at the south of the New Territories. The SCVA covers the foothill area of Tai Mo Shan in Tsuen Wan. Fu Yung Shan is to the west of the SCVA, Tsuen Wan is to the southwest, Kwai Chung is to the southeast, and Tai Mo Shan Country Park and Shing Mun Country Park are to the north. The SCVA is generally hilly with a maximum elevation of about +440 mPD. A majority of the SCVA, including its central and northern portions, encroaches onto Tai Mo Shan Country Park and Shing Mun Country Park. -

Minutes of 673Rd Meeting of the Rural and New Town Planning
TOWN PLANNING BOARD Minutes of 673rd Meeting of the Metro Planning Committee held at 9:00 a.m. on 11.6.2021 Present Director of Planning Chairman Mr Ivan M.K. Chung Mr Wilson Y.W. Fung Vice-chairman Dr Frankie W.C. Yeung Dr Lawrence W.C. Poon Mr Alex T.H. Lai Professor T.S. Liu Ms Sandy H.Y. Wong Mr Franklin Yu Mr Stanley T.S. Choi Mr Daniel K.S. Lau Ms Lilian S.K. Law Professor John C.Y. Ng Professor Jonathan W.C. Wong - 2 - Dr Roger C.K. Chan Assistant Commissioner for Transport (Urban), Transport Department Mr Patrick K.H. Ho Chief Engineer (Works), Home Affairs Department Mr Gavin C.T. Tse Principal Environmental Protection Officer (Metro Assessment), Environmental Protection Department Dr Sunny C.W. Cheung Assistant Director (Regional 1), Lands Department Mr Albert K.L. Cheung Deputy Director of Planning/District Secretary Miss Fiona S.Y. Lung Absent with Apologies Mr Thomas O.S. Ho Mr C.H. Tse In Attendance Assistant Director of Planning/Board Ms Lily Y.M. Yam Chief Town Planner/Town Planning Board Ms Caroline T.Y. Tang Town Planner/Town Planning Board Ms Andrea W. Y. Yan - 3 - Opening Remarks 1. The Chairman said that the meeting would be conducted with video conferencing arrangement. Agenda Item 1 Confirmation of the Draft Minutes of the 672nd MPC Meeting held on 28.5.2021 [Open Meeting] 2. The draft minutes of the 672nd MPC meeting held on 28.5.2021 were confirmed without amendments. Agenda Item 2 Matter Arising [Open Meeting] 3. -

Location/Activities Address Nearest MTR Line Travel from the Dorsett Hotel Hotel
Location/Activities Address Nearest MTR Line Travel from the Dorsett Hotel Hotel Dorsett Tsuen Wan Hotel 28 Kin Chuen Street, Kwai Tai Wo Hau Station Tsuen Wan Line (Red) N/A Chung, Kowloon, Hong Kong Link to street map Cultural Activities Disneyland Lantau Island, Hong Kong (to Disneyland Resort Station Disneyland Resort Line MTR meet at the park entrance) Link to street map (Pink) - Tai Wo Hau Station - Tsuen Wan Line (Red) - Change at Lai King (platform 3 towards Tung Chung) - Tung Chung Line (Orange) - Change at Sunny Bay (platform 3) - Disneyland Resort Line (Pink) Evening Harbour Cruise Tsim Sha Tsui Public Pier 1, Tsim Sha Tsui Station Tsuen Wan Line (Red) MTR Tsim Sha Tsui, Hong Kong Link to street map - Tai Wo Hau Station - Tsuen Wan Line (Red) Walking from Tsim Sha Tsui Station - Make your way to exit L6 - Cross Salisbury Road - Pier 1 is right behind the Cultural Centre on your right (close to the Clock Tower) Guide map Po Lin Monastery & Big Buddha Ngong Ping Cable Car, 11 Tat Tung Chung Station Tung Chung Line MTR Tung Rd, Lantau Island, Hong Link to street map (Orange) - Tai Wo Hau Station Kong (to meet at Ngong Ping - Tsuen Wan Line (Red) Cable Car Tung Chung) - Change at Lai King (platform 3 towards Tung Chung) - Tung Chung Line (Orange) Walking from Tung Chung Station - Leave the station through Exit B - Tung Chung Cable Car Terminal is adjacent to the Exit B Guide Map Victoria Peak & Tram The Peak Tram Lower Central Station Tung Chung Line MTR Terminus, Garden Road, Link to street map (Orange) - Tai Wo Hau Station Central