DOCSLIB.ORG

C O L L E C T I V E N U C L E a R S T R U C T U R E STUDIES in T H E O S M I U M NUCLEI by Richard F. Casten B. S. , College Of

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
C O L L E C T I V E N U C L E a R S T R U C T U R E STUDIES in T H E O S M I U M NUCLEI by Richard F. Casten B. S. , College Of COLLECTIVE NUCLEAR STRUCTURE STUDIES IN THE OSMIUM NUCLEI by Richard F. Casten B. S. , College of the Holy Cross, 1963 M. S. , Yale University , 1964 A Dissertation Presented to the Faculty of the Graduate School of Yale University in Candidacy for the Degree of Doctor of Philosophy 1967 T o m y father, m y mother, and to Jo-Ann ABSTRACT Collective nuclear structure studies on the four even-even isotopes of o^gaiuxn, Os'®8 . 188, 190, 192 have been pursued using Co u l o m b excitation induced by O ions with incident energies between 42 and 80 M e V obtained from the Yale M P T a n d e m V a n de Graaff accelerator. The o s m i u m isotopes span the important transition region from highly deformed to nearly spherical nuclei located at the high mass extremity of the rare earth region of collectivity and they have therefore long been the center of mu c h theoretical and experimental interest. The deexcitation radiation has been observed singly, in coincidence with o'6 ions backscattered from the target, and in coincidence with other y-rays representing the 2+ -* 0+ and 4+ -* 2+ transitions in each isotope. In Os'®8 ’ '®®> '®8 all levels through the 6+ state of the ground state rotational band as well as the 2+I and 4 ' levels of the so-called y-vibrational band have been excited. In Os'®® an additional 0+ level at 1086 kev w a s observed while in Os'®^ all kn o w n states except the unnatural parity 3+ level were detected. Furthermore, in Os'®®, Os'®®, and Os'®^ ne w states at 780, 840, and 855 kev, respectively, are tentatively proposed with J71-assignments of 2+ or 3~ ascribed as likely and not inconsistent with any of our measurements. The m ain emphasis has been on the extraction of absolute reduced transition probabilities (B(E2) values). These have been obtained, for the excitation of all states previously known, by both model-dependent and model-independent analyses. The results have been compared with several macroscopic and microscopic nuclear models, with particular attention to that of Ku m a r and Baranger. The latter has proved the most complete and successful of any in predicting both absolute B(E2) values and the variations of these with neutron nu m b e r in the o s m i u m isotopes. The trend toward the spherical or vibrational limit in Os'®2 is calculated to be somewhat sharper than is observed experimentally. Suggestions are made for possible improvements in the pairing-plus-quadrupole model of these authors. A n interpretation of the o s m i u m isotopes as typified by shallow potential m i n i m a for moderately prolate deformations (and slightly axially asymmetric equilibrium configurations in Os'®®> '®^) and by extreme softness to vibrations in both /3 and y em e r g e s from this comparison and is actually confirmed by both the successes and failures of the other models with which comparisons are made. Discussion is also m a d e of the possible existence and implications of finite excited state quadrupole moments predicted in osmium by Ku m a r and Baranger and in other spherical nuclei by other authors. Finally, suggestions for future experimental tests of the theoretical calculations in this transition region are offered. ACKNOWLEDGEMENTS It is a great pleasure to acknowledge m y appreciation to Dr. J. S. Greenberg and to Prof. D. A. B r o m l e y wh o supervised the research performed here. I would like to thank Dr. Greenberg for his advice and participation in all phases of this work and for the guidance in the data analysis provided by his probing questions and suggestions. I a m very deeply indebted to Prof. B r o m l e y not only for making available the facilities of the A. W . Wright Nuclear Structure Laboratory of Yale University but also especially for numerous invaluable discussions concerning this work and for his generous support and counsel in so many matters. I a m indebted to Dr. K. K u m a r for discussions concerning his calculations and for communication of certain results of those calculations prior to their publication. I a m grateful to Dr. G. A. Burginyon for his extensive cooperation and advice in the collection and analysis of the data presented herein, for his help with the c o m ­ puter pr o g r a m s and for innumerable discussions concerning ma n y facets of this work. Thanks are also extended to S. Sie for help in the later phases of data acquisition. I would like to thank the entire faculty of the Nuclear Structure Laboratory, as well as m y fellow graduate students there, for the m a n y interesting discussions dealing with all aspects of nuclear physics. I would also like to express m y appreciation to the entire operating and support staffs of the accelerator for their continual assistance and ready cooperation during the course of these measurements and during the preparation of this final manuscript. I would like to thank m y wife, Jo-Ann, for her constant encouragement and, in particular, for typing the various drafts and the final manuscript of this thesis. N o aspect of this work would have been even remotely possible were it not for the singularly unfailing lifelong support, encouragement, guidance and stim­ ulation of m y father to w h o m I can in no wa y express sufficient gratitude and appreciation. T h e inspiration and example he has provided will never be forgotten. I a m indebted to the Danforth Foundation for its abiding interest in all aspects of m y graduate education and for its grants which supported that education in particularly tangible fashion. Finally, I would like to thank the United States Atomic Energy Co m m i s s i o n for financial support of this research. TABLE OF CONTENTS ABSTRACT ACKNOWLEDGEMENTS ORIENTATION ....................................................... I THEORETICAL CONSIDERATIONS ..................................... 5 A. Macroscopic Models .............................................. 5 B. Microscopic M odels............................................... 14 C. Coulomb Excitation Theory......................................... 29 EXPERIMENTAL CONSIDERATIONS ................................... 40 A. Methods of Me a s u r e m e n t ........................................... 40 B. Accelerator...................................................... 43 C . Scattering Chamber and Particle and G a m m a Ray Detection Apparatus.................................... 45 D. Targets........................................................... 48 E. Electronics....................................................... 50 DATA PRESENTATION AND DECAY SCHEMES ......................... 52 A. Orientation....................................................... 52 B. O s 186............................................................. 55 C. O s 188............................... * ............................ 58 D. O s 19°............................................................. 62 E. O s 192............................................................. 64 DATA ANALYSIS ..................................................... 66 A. Data Reduction.................................................... 66 B. Extraction of Nuclear Information.................................. 75 C. Perturbation Theory Analysis...................................... 79 D. Model Dependent Calculations...................................... 82 E. Complete Calculation via the Coupled Schrodinger Equations..................................... 84 F. Err o r s ........................................................... .86 PRESENTATION AND INTERPRETATION OF EXPERIMENTAL RESULTS. 88 VII. SUMMARY AND SUGGESTIONS ............................................ 112 VUI. APPENDICES ...................................... 119 Appendix 1................................................................ 119 Appendix II............................................................... 125 IX. REFERENCES ........................................................... 139 I. ORIENTATION There is as yet no exact mathematical technique for the complete calcu­ lation of the properties of a many-body quantum mechanical system. Except for its lightest representatives, the atomic nucleus in general constitutes such a system. In addition, even if such a mathematical apparatus were available, the nuclear (or nucleon-nucleon) force is only very imperfectly known. In order to m a k e progress in the elucidation of nuclear structure one must therefore m a k e certain mathematical and physical assumptions and approximations. The recent history of nuclear structure physics has consisted largely of a succession of such nuclear models and has been characterized by a steadily improving accord between them and the experimental facts which encourage and test them. Broadly speaking, there are two striking features revealed by the data of nuclear physics: the nearly independent motion of the nucleons in the nucleus and the strong correlations a m o n g the motions of ma n y nucleons resulting in apparently collective behaviour. These two seemingly contradictory aspects have given rise to two general models of nuclear structure, the shell model and the collective model. Both of these, of course, have m a n y variants. The earliest collective models were "phenomenological" in that they pos­ tulated, without derivation, that the nucleus possessed certain gross properties implied by the data. Thus, for example, in order to explain certain features of the data recognizable as similar to those of a rotating symmetric, quantum m e ­ chanical top, the nucleus was consequently assumed to be deformed and to rotate. No accounting
Load more

Recommended publications
  • The Separation and Determination of Osmium and Ruthenium
    Louisiana State University LSU Digital Commons LSU Historical Dissertations and Theses Graduate School 1969 The epS aration and Determination of Osmium and Ruthenium. Harry Edward Moseley Louisiana State University and Agricultural & Mechanical College Follow this and additional works at: https://digitalcommons.lsu.edu/gradschool_disstheses Recommended Citation Moseley, Harry Edward, "The eS paration and Determination of Osmium and Ruthenium." (1969). LSU Historical Dissertations and Theses. 1559. https://digitalcommons.lsu.edu/gradschool_disstheses/1559 This Dissertation is brought to you for free and open access by the Graduate School at LSU Digital Commons. It has been accepted for inclusion in LSU Historical Dissertations and Theses by an authorized administrator of LSU Digital Commons. For more information, please contact [email protected]. ThU dissertation has been 69-17,123 microfilmsd exactly as received MOSELEY, Harry Edward, 1929- THE SEPARATION AND DETERMINATION OF OSMIUM AND RUTHENIUM. Louisiana State University and Agricultural and Mechanical College, PhJ>., 1969 Chemistry, analytical University Microfilms, Inc., Ann Arbor, Michigan THE SEPARATION AND DETERMINATION OF OSMIUM AND RUTHENIUM A Dissertation Submitted to the Graduate Faculty of the Louisiana State University and Agricultural and Mechanical College in partial fulfillment of the requirements for the degree of Doctor of Philosophy in The Department of Chemistry Harry Edward Moseley B.S., Lpuisiana State University, 1951 M.S., Louisiana State University, 1952 J anuary, 1969 ACKNOWLEDGMENTS Thanks are due to Dr. Eugene W. Berg under whose direction this work was performed, to Dr. A. D. Shendrikar for his help in the tracer studies, and to Mr. J. H. R. Streiffer for his help in writing the com­ puter program.
    [Show full text]
  • Jahresbericht 2007
    IKMz 2008- 1 ISSN 0932-7622 INSTITUT FÜR KERNCHEMIE UNIVERSITÄT MAINZ JAHRESBERICHT 2007 August 2008 FRITZ-STRASSMANN-WEG 2, D-55128 MAINZ, TELEFON (06131) 3925879, TELEFAX (06131) 3925253 Kernchemie im Internet Das Institut für Kernchemie der Universität Mainz ist mit einer Homepage im World Wide Web vertreten. Unter der Adresse http://www.kernchemie.uni-mainz.de finden Sie aktuelle Informationen zum Institut, seinen Mitarbeitern, den Lehrveranstaltungen und den Forschungsaktivitäten. Die in diesem Bericht vorgelegten Ergebnisse stammen zum Teil aus noch nicht abgeschlossenen Arbeiten und sind daher als vorläufige Mitteilung zu bewerten. INSTITUT FÜR KERNCHEMIE UNIVERSITÄT MAINZ JAHRESBERICHT 2007 Herausgeber: Frank Rösch Mainz, im August 2008 Vorwort Der vorliegende Jahresbericht 2007 gibt einen Überblick über die wissenschaftlichen Aktivitäten des Instituts für Kernchemie. Er legt damit gleichzeitig all denen, die uns in ideeller und finanzieller Weise gefördert haben, Rechenschaft ab über die Verwendung nicht unerheblicher öffentlicher Mittel. Außerdem beschreibt er den Status der technischen Einrichtungen des Instituts und technische Neu- entwicklungen. Schließlich stellt er die Ergebnisse des Instituts in Form von Publikationen, Konferenzbeiträgen, Dissertationen, Diplom- und Staatsexamensarbeiten sowie die Beiträge seiner Hochschullehrer in der Lehre und Weiterbildung dar. Der wissenschaftliche Bericht umfasst die drei Forschungsschwerpunkte: • Kernchemie im Sinne grundlegender Fragestellungen, • Radiopharmazeutische Chemie und Anwendung radiochemischer Methoden mit medizinischer Zielsetzung, • Hochempfindliche und –selektive Analytik für umweltrelevante, technische und biologische Probleme. Im August 2007 hat der Präsident unserer Universität, Herr Prof. Dr. Krausch, die Laufzeit des Forschungsreaktors TRIGA Mainz bis zunächst 2020 verlängert. Die Carl-Zeiss-Stiftung hat 2007 die Einrichtung einer Juniorprofessur für das Thema „Ultrakalte Neutronen“ am Institut für Kernchemie ab 2008 ermöglicht.
    [Show full text]
  • Rotation Aligned Negative Parity Side Bands in Light Tungsten and Osmium Nuclei G.D
    ROTATION ALIGNED NEGATIVE PARITY SIDE BANDS IN LIGHT TUNGSTEN AND OSMIUM NUCLEI G.D. Dracoulis To cite this version: G.D. Dracoulis. ROTATION ALIGNED NEGATIVE PARITY SIDE BANDS IN LIGHT TUNG- STEN AND OSMIUM NUCLEI. Journal de Physique Colloques, 1980, 41 (C10), pp.C10-66-C10-78. 10.1051/jphyscol:19801007. jpa-00220626 HAL Id: jpa-00220626 https://hal.archives-ouvertes.fr/jpa-00220626 Submitted on 1 Jan 1980 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. JOURNAL DE PHYSIQUE CoZZoque CIO, suppZe'ment au n012, Tome 41, de'cembre 1980, page C10-66 ROTATION ALIGNED NEGATIVE PARITY SIDE BANDS IN LIGHT TUNGSTEN AND OSMIUM NUCLEI G.D. Dracoulis. Department of Nuclear Physics, Research SchooZ of PhysicaZ Sciences, Australian National University, P. 0. Box 4, A. C. T. Canberrra, Australia. Abstract.- Rotation aligned negative parity sidebands have been observed in the light Tungsten and Osmium isotopes. The development from octupole bands to aligned 2-quasiparticle bands is discussed. The hghproton and i13/2 neutron are the likely configurations causing the alignment. Backbending observed in the odd spin negative parity sidebands in lEOOs suggests that both proton and neutron configurations are involved at high spin.
    [Show full text]
  • Accelerator-Based Production of High Specific Activity Radionuclides for Radiopharmaceutical Applications
    ACCELERATOR-BASED PRODUCTION OF HIGH SPECIFIC ACTIVITY RADIONUCLIDES FOR RADIOPHARMACEUTICAL APPLICATIONS A Dissertation Presented to the Faculty of the Graduate School at the University of Missouri-Columbia In Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy By MATTHEW DAVID GOTT Dr. Silvia S. Jurisson, Dissertation Advisor Dr. Cathy S. Cutler, Co-Advisor JULY 2015 The undersigned, appointed by the dean of the Graduate School, have examined the dissertation entitled ACCELERATOR-BASED PRODUCTION OF HIGH SPECIFIC ACTIVITY RADIONUCLIDES FOR RADIOPHARMACEUTICAL APPLICATIONS presented by Matthew David Gott, a candidate for the degree of Doctor of Philosophy, and hereby certify that, in their opinion, it is worthy of acceptance. Dr. Silvia S. Jurisson Dr. Cathy S. Cutler Dr. C. Michael Greenlief Dr. J. David Robertson DEDICATION This dissertation is dedicated to my wonderful parents, David and Cathy. You have always been my greatest supporters and encouraged me every step of the way. None of this would have been possible without you. ACKNOWLEDGMENTS I would like to thank Dr. C. Michael Greenlief and Dr. J. David Roberston for serving on my committee and providing advice throughout this process. I would like to thank all of my collaborators who provided assistance and guidance throughout this project. Dr. Donald Wycoff, Dr. Anthony Degraffenreid, and Yutian Feng were instrumental in the arsenic production work. Dr. Alan Ketring, Dr. John Lydon, Mary Embree, Stacy Wilder, Alex Saale, Melissa Evans-Blumer, and the staff at the University of Missouri Research Reactor provided support and ideas for experimental work throughout this dissertation. Dr. Michael Fassbender, Dr. Beau Ballard, and the members of the C-IIAC group at Los Alamos National Laboratory provided assistance and guidance with the experimental work for the W/Re separation method.
    [Show full text]
  • Lawrence Berkeley National Laboratory Recent Work
    Lawrence Berkeley National Laboratory Recent Work Title ALPHA DECAY OF NEUTRON DEFICIENT OSMIUM ISOTOPES Permalink https://escholarship.org/uc/item/83k5c4rq Authors Borggreen, Jorn Hyde, Earl K. Publication Date 1970-07-01 eScholarship.org Powered by the California Digital Library University of California Submitted to Nuclear ·physics UCRL-19596 Pre print c ,_ 2... ALPHA DECAY OF NEUTRON DEFICIENT OSMIUM ISOTOPES, Jj&'rn Borggreen and Earl K. Hyde July 1970 AEC Contract No. W-7 405 -eng -48 ·-r:tVED 'NRf.HCE TWO-WEEK lOAN COPY . ,ui4 UBORATO~ This is a Library Circulating Copy . u~ I - 1197~ which may be borrowed for two weeks. LIBRARY J: For a personal retention copy, call ,QCUMENTS ~ Tech. Info. Division, Ext. 5545 LAWRENCE RADIATION LABORATORY ' UNIVERSITY of CALIFORNIA BERKELEY \ DISCLAIMER · This document was prepared as an account of work sponsored by the United States Government. While this document is believed to contain correct information, neither the United States Government nor any agency thereof, nor the Regents of the University of California, nor any of their employees, makes any warranty, express or implied, or assumes any legal responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by its trade name, trademark, manufacturer, or otherwise, does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof, or the Regents of the University of Califomia. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Govemment or any agency thereof or the Regents of the University of Califomia.
    [Show full text]
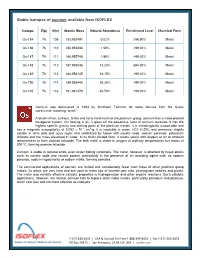
  • Stable Isotopes of Osmium Available from ISOFLEX
    Stable isotopes of osmium available from ISOFLEX Isotope Z(p) N(n) Atomic Mass Natural Abundance Enrichment Level Chemical Form Os-184 76 108 183.952491 0.02% ≥96.90% Metal Os-186 76 110 185.953838 1.59% >99.00% Metal Os-187 76 111 186.955748 1.96% >99.00% Metal Os-188 76 112 187.955836 13.24% ≥94.00% Metal Os-189 76 113 188.958145 16.15% >99.00% Metal Os-190 76 114 189.958445 26.26% >99.00% Metal Os-192 76 116 191.961479 40.78% >99.00% Metal Osmium was discovered in 1803 by Smithson Tennant. Its name derives from the Greek word osme, meaning “smell.” A bluish-white, lustrous, brittle and fairly hard metal of the platinum group, osmium has a close-packed hexagonal system. On heating in air, it gives off the poisonous fume of osmium tetroxide. It has the highest specific gravity and melting point of the platinum metals. It is metallurgically unworkable and -6 3 has a magnetic susceptibility of 0.052 x 10 cm /g. It is insoluble in water, HCl, H2SO4 and ammonia; slightly soluble in nitric acid and aqua regia; and solubilized by fusion with caustic soda, sodium peroxide, potassium chlorate and the mass dissolved in water. In its finely divided form, it reacts slowly with oxygen or air at ambient temperatures to form osmium tetroxide. The bulk metal is stable in oxygen at ordinary temperatures but reacts at 200 ºC, forming osmium tetroxide. Osmium is stable in mineral acids, even under boiling conditions.
    [Show full text]
  • Determination of the Isotopic Composition of Osmium Using MC-ICPMS Zhu, Zuhao; Meija, Juris; Tong, Shuoyun; Zheng, Airong; Zhou, Lian; Yang, Lu
    NRC Publications Archive Archives des publications du CNRC Determination of the isotopic composition of osmium using MC-ICPMS Zhu, Zuhao; Meija, Juris; Tong, Shuoyun; Zheng, Airong; Zhou, Lian; Yang, Lu This publication could be one of several versions: author’s original, accepted manuscript or the publisher’s version. / La version de cette publication peut être l’une des suivantes : la version prépublication de l’auteur, la version acceptée du manuscrit ou la version de l’éditeur. For the publisher’s version, please access the DOI link below./ Pour consulter la version de l’éditeur, utilisez le lien DOI ci-dessous. Publisher’s version / Version de l'éditeur: https://doi.org/10.1021/acs.analchem.8b01859 Analytical Chemistry, 90, 15, pp. 9281-9288, 2018-06-21 NRC Publications Archive Record / Notice des Archives des publications du CNRC : https://nrc-publications.canada.ca/eng/view/object/?id=45709299-174b-4f06-91d3-411ee9765217 https://publications-cnrc.canada.ca/fra/voir/objet/?id=45709299-174b-4f06-91d3-411ee9765217 Access and use of this website and the material on it are subject to the Terms and Conditions set forth at https://nrc-publications.canada.ca/eng/copyright READ THESE TERMS AND CONDITIONS CAREFULLY BEFORE USING THIS WEBSITE. L’accès à ce site Web et l’utilisation de son contenu sont assujettis aux conditions présentées dans le site https://publications-cnrc.canada.ca/fra/droits LISEZ CES CONDITIONS ATTENTIVEMENT AVANT D’UTILISER CE SITE WEB. Questions? Contact the NRC Publications Archive team at [email protected]. If you wish to email the authors directly, please see the first page of the publication for their contact information.
    [Show full text]
  • PLATINUM METALS REVIEW a Quarterly Survey of Research on the Platinum Metals and of Developments in Their Application in Industry
    E-ISSN 1471–0676 PLATINUM METALS REVIEW A Quarterly Survey of Research on the Platinum Metals and of Developments in their Application in Industry www.platinummetalsreview.com VOL. 48 OCTOBER 2004 NO. 4 Contents Ruthenium Vinylidene Complexes 148 By Valerian Dragutan and Ileana Dragutan 13th International Congress on Catalysis 154 A conference review by Alvaro Amieiro-Fonseca, Janet M. Fisher and Sonia Garcia Oxidation States of Ruthenium and Osmium 157 A book review by C. F. J. Barnard and S. C. Bennett Iridium-Based Hexacyanometallate Thin Films 159 in Aqueous Electrolytes By Kasem K. Kasem and Leslie Huddleston Increased Luminescent Lifetimes of Ru(II) Complexes 168 Carbon Nanotube Particulates in Electron Emitters 168 Palladium-Iron Dispersed in Carbon 168 Catalysis by Gold/Platinum Group Metals 169 By David T. Thompson The Discoverers of the Osmium Isotopes 173 By J. W. Arblaster Fundamentals of Kinetics and Catalysis 180 A book review by Tim Watling Bicentenary of Four Platinum Group Metals 182 By W. P. Griffith Abstracts 190 New Patents 193 Indexes to Volume 48 195 Communications should be addressed to: The Editor, Susan V. Ashton, Platinum Metals Review, [email protected] Johnson Matthey Public Limited Company, Hatton Garden, London EC1N 8EE DOI: 10.1595/147106704X4835 Ruthenium Vinylidene Complexes SYNTHESES AND APPLICATIONS IN METATHESIS CATALYSIS By Valerian Dragutan* and Ileana Dragutan Institute of Organic Chemistry, Romanian Academy, 202B Spl. Independentei, PO Box 15-254, 060023 Bucharest, Romania; *E-mail: [email protected] This paper surveys an attractive family of ruthenium complexes with great potential for applications in organic and polymer synthesis. When compared with traditional ruthenium alkylidene pre-catalysts, these alternative ruthenium vinylidene complexes are easily accessible from commercial starting materials.
    [Show full text]
  • Lead: Properties, History, and Applications Mikhail Boldyrev¹*, Et Al
    WikiJournal of Science, 2018, 1(2):7 doi: 10.15347/wjs/2018.007 Encyclopedic Review Article Lead: properties, history, and applications Mikhail Boldyrev¹*, et al. Abstract Lead is a chemical element with the atomic number 82 and the symbol Pb (from the Latin plumbum). It is a heavy metal that is denser than most common materials. Lead is soft and malleable, and has a relatively low melting point. When freshly cut, lead is silvery with a hint of blue; it tarnishes to a dull gray color when exposed to air. Lead has the highest atomic number of any stable element and concludes three major decay chains of heavier elements. Lead is a relatively unreactive post-transition metal. Its weak metallic character is illustrated by its amphoteric nature; lead and its oxides react with acids and bases, and it tends to form covalent bonds. Compounds of lead are usually found in the +2 oxidation state rather than the +4 state common with lighter members of the carbon group. Exceptions are mostly limited to organolead compounds. Like the lighter members of the group, lead tends to bond with itself; it can form chains, rings and polyhedral structures. Lead is easily extracted from its ores; prehistoric people in Western Asia knew of it. Galena, a principal ore of lead, often bears silver, interest in which helped initiate widespread extraction and use of lead in ancient Rome. Lead production declined after the fall of Rome and did not reach comparable levels until the Industrial Revolution. In 2014, annual global production of lead was about ten million tonnes, over half of which was from recycling.
    [Show full text]
  • Lawrence Berkeley National Laboratory Recent Work
    Lawrence Berkeley National Laboratory Recent Work Title NEUTRON-DEFICIENT IRIDIUM ISOTOPES Permalink https://escholarship.org/uc/item/1780k0z2 Authors Diamond, R.M. Hollander, J.M. Publication Date 1958-03-01 eScholarship.org Powered by the California Digital Library University of California UCRL sl96 UNIVERSIT-Y OF CALIFORNIA TWO-WEEK LOAN COPY This is a Library Circulating Copy which may be borrowed for two weeks. For a personal retention copy, call Tech. Info. Division, Ext. 5545 BERKELEY. CALIFORNIA DISCLAIMER This document was prepared as an account of work sponsored by the United States Government. While this document is believed to contain correct information, neither the United States Government nor any agency thereof, nor the Regents of the University of California, nor any of their employees, makes any warranty, express or implied, or assumes any legal responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by its trade name, trademark, manufacturer, or otherwise, does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof, or the Regents of the University of California. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof or the Regents of the University of California. ,. UCRL-8196 UNIVERSITY OF CALIFORNIA ' t· .. Radiation Laboratory ·~~ Berkeley, California Contract No. W-7405-eng-48 NEUTRON-DEFICIENT IRIDIUM ISOTOPES R. M.
    [Show full text]
  • Stdin (Ditroff)
    60Sa01 D. Sadeh, Phys. Rev. Letters 4, 75 (1960). Nuclear Structure: 16O; measured not abstracted; deduced nuclear properties. 60Sa02 G. J. Safford, B. M. Rustad, W. W. Havens, Jr., Bull. Am. Phys. Soc. 5, No. 1, 33, I6 (1960). Nuclear Structure: 235U, 233U; measured not abstracted; deduced nuclear properties. 60Sa03 Y. Saji, J. Phys. Soc. Japan 15, 367(1960). Nuclear Structure: 9B; measured not abstracted; deduced nuclear properties. 60Sa04 G. J. Safford, T. I. Taylor, B. M. Rustad, W. W. Havens, Jr., Bull. Am. Phys. Soc. 5, No. 4, 288, WA6 (1960) Nuclear Structure: 10B, B; measured not abstracted; deduced nuclear properties. 60Sa05 Short-Lived Bromine and Selenium Nuclides from Fission J. E. Sattizahn, J. D. Knight, J. Inorg. Nuclear Chem. 12, 206 (1960). Nuclear Structure: 87Se, 87Br, 84Se, 84Br, 85Se; measured not abstracted; deduced nuclear properties. 60Sa06 Z. Sawa, Arkiv Fysik 16, 519A (1960). Nuclear Structure: 4He; measured not abstracted; deduced nuclear properties. 60Sa07 J. Sanada, K. Nisimura, S. Suwa, I. Hayashi, F. Fukunaga, N. Ryu, M. Seki, J. Phys. Soc. Japan 15, 754 (1960). Nuclear Structure: 4He, 5Li; measured not abstracted; deduced nuclear properties. 60Sa08 Precision Measurement of the Total Neutron Cross Section of U233 between 0.000818 and 0.0818 eV G. J. Safford, W. W. Havens, Jr., B. M. Rustad, Phys. Rev. 118, 799 (1960). Nuclear Structure: 238U; measured not abstracted; deduced nuclear properties. 60Sa09 D. Sadeh, Compt. Rend. 250, 1632 (1960). Nuclear Structure: 14N, 19F; measured not abstracted; deduced nuclear properties. 60Sa10 Decay of Ruthenium-105 B. Saraf, P. Harihar, R. Jambunathan, Phys. Rev. 118, 1289 (1960).
    [Show full text]
  • Subcommittee on Nuclear and Radiochemistry Committee on Chemical Sciences Assembly of Mathematical and Physical Sciences National Research Council
    SEPARATED ISOTOPES: cnrp-Rono'*-* c-nmn VITAL TOOLS TOR SCIENCE AND MEDICINE C0LF 820233 — Summ. DE33 011646 Subcommittee on Nuclear and Radiochemistry Committee on Chemical Sciences Assembly of Mathematical and Physical Sciences National Research Council DISCLAIMER This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsi- bility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Refer- ence herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recom- mendation, or favoring by the United States Governmenl or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. NATIONAL ACADEMY PRESS Washington, D.C. 1982 \P DISTR1BUT10II Of THIS DOCUMENT IS UNLIMITED NOTICE: The project that is the subject of this report was approved by the Governing Board of the National Research Council, whose members are drawn from the Councils of the National Academy of Sciences, the Nationcil Academy of Engineering, and the Institute of Medicine. The members of the Committee responsible for the report were chosen for their special competences and with regard for appropriate balance. This report has been reviewed by a group other than the authors according to procedures approved by a Report Review Committee consisting of members of the National Academy of Sciences, the National Academy of Engineering, and the Institute of Medicine.
    [Show full text]