Review the Denotations of Intransitive Verbs
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Chapter Ii the Types of Phrasal Verbs in Movie Snow White and the Huntsman by Rupert Sanders
33 CHAPTER II THE TYPES OF PHRASAL VERBS IN MOVIE SNOW WHITE AND THE HUNTSMAN BY RUPERT SANDERS In this chapter, the researcher will analyzed the types of phrasal verbs. It is to complete the first question in this research. The researcher had been categorizing the types of phrasal verbs and form that divided into verb and adverb, also sometimes prepositions. 2.1. Types of Phrasal Verbs in movie Snow White and the Huntsman According to Heaton (1985:103) considers that phrasal verbs are compound verbs that result from combining a verb with an adverb or a preposition, the resulting compound verb being idiomatic. Phrasal verb is one of important part of grammar that almost found in English language. Based on Andrea Rosalia in her book “A Holistic Approach to Phrasal Verb”, Phrasal verbs are considered to be a very important and frequently occurring feature of the English language. First of all, they are so common in every day conversation, and non-native speakers who wish to sound natural when speaking this language need to learn their grammar in order to know how to produce them correctly. Secondly, the habit of inventing phrasal verbs has been the source of great enrichment of the language (Andrea Rosalia, 2012:16). A grammarian such as Eduard, Vlad (1998:93) describes phrasal verbs as "combinations of a lexical verb and adverbial particle". It means that the verb if wants to be a phrasal verb always followed by particle. It can be one particle or two particles in one verb. If the case is like that, it called as multi word verbs. -

Ling 130 Notes: Predicate Logic and English Syntax
Ling 130 Notes: Predicate Logic and English Syntax Sophia A. Malamud February 15, 2011 1 Characteristic functions The characteristic function of a set: (1) Let A be a set. The, charA, the characteristic function of A, is the function F such that, for any x∈ A, F(x)=1, and for any x ∉ A, F(x)=0. Schönfinkelization: (2) U = {a,b,c} (3) The relation "fond of": Rfond-of = {<a,b>, <b,c>, <c,c>} (4) The characteristic function of Rfond-of (takes all combinations of two elements, gives 0/1): <a,a> →0 <a,b> →1 <a,c> →0 <b,a> →0 CharRfond-of = <b,b> →0 <b,c> →1 <c,a> →0 <c,b> →0 <c,c> →1 (5) Turning n-ary functions into multiple embedded 1-ary functions: Schönfinkelization. a → 0 left-to-right schönfinkelization a →b → 1 c → 0 a → 0 b →b → 0 c → 1 a → 0 c →b → 0 c → 1 EXERCISE 1: Given the following Universe, spell out the characteristic function of the set in (6) and schönfinkelize it left-to-right. 1 (6) U = {d, e} (7) R = { <d,d,d>, <d,e,d>, <e,d,d>, <e,e,e>, <e,e,d> } 2 Syntactic composition A formal language is a set of strings - finite sequences of minimal units (words/morphemes, for natural languages) - with meaning. The "machine" that generates those strings and their corresponding meanings is its grammar. A grammar must specify the following three components: • A lexicon which contains every minimal unit with meaning (= every word, for this course) and its grammatical category; • a syntax, that is, a set of rules that tells you how the minimal units combine to form longer units, how this longer units combine to form yet longer units, and so forth until we form full complex sentences; and • a semantics, which determines what semantic operation or function corresponds to each syntactic rule and combines the “atomic” word meanings to build the meaning of the complete sentence. -

Serial Verb Constructions Revisited: a Case Study from Koro
Serial Verb Constructions Revisited: A Case Study from Koro By Jessica Cleary-Kemp A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Linguistics in the Graduate Division of the University of California, Berkeley Committee in charge: Associate Professor Lev D. Michael, Chair Assistant Professor Peter S. Jenks Professor William F. Hanks Summer 2015 © Copyright by Jessica Cleary-Kemp All Rights Reserved Abstract Serial Verb Constructions Revisited: A Case Study from Koro by Jessica Cleary-Kemp Doctor of Philosophy in Linguistics University of California, Berkeley Associate Professor Lev D. Michael, Chair In this dissertation a methodology for identifying and analyzing serial verb constructions (SVCs) is developed, and its application is exemplified through an analysis of SVCs in Koro, an Oceanic language of Papua New Guinea. SVCs involve two main verbs that form a single predicate and share at least one of their arguments. In addition, they have shared values for tense, aspect, and mood, and they denote a single event. The unique syntactic and semantic properties of SVCs present a number of theoretical challenges, and thus they have invited great interest from syntacticians and typologists alike. But characterizing the nature of SVCs and making generalizations about the typology of serializing languages has proven difficult. There is still debate about both the surface properties of SVCs and their underlying syntactic structure. The current work addresses some of these issues by approaching serialization from two angles: the typological and the language-specific. On the typological front, it refines the definition of ‘SVC’ and develops a principled set of cross-linguistically applicable diagnostics. -

The Relationship Between Transitive and Intransitive Verbs in English Language
NOTION NOTION Volume 01, Number 02, November 2019 p. 62-67 The Relationship between Transitive and Intransitive Verbs in English Language Teddy Fiktorius SMA Bina Mulia Pontianak, Kalimantan Barat, Indonesia [email protected] Article Info ABSTRACT Article History In the current research, the researcher employs descriptive method (library Article Received research) to elaborate on the relationship and differentiation between the 17th August 2019 English language transitive and intransitive verbs. The first parts explore the Article Reviewed theoretical framework of the relationship and differentiation equipped with 9th September 2019 various sentences samples. The next part discusses the implications for English Article Accepted language teachers in coping with some grammatical confusion. Finally, some 11 October 2019 solutions as well as recommendations are proposed. Keywords transitive verbs intransitive verbs grammatical confusion I. INTRODUCTION misleading sentences that lose its exact meaning. Verbs can be so tricky that even the best grammar Students, particularly the speakers of other languages, students might be often confounded by the difference often have difficulty determining which verbs require between transitive and intransitive verbs. The an object, and which do not. When students confuse confusion with the use of the transitive and transitive and intransitive verbs, the sentences they intransitive verbs can be resolved as a grammar point construct both orally and in written may be becomes clear with an understanding of objects. incomplete. When using a dictionary to look up verbs, we may This current paper is written to provide us with have been puzzled by the abbreviations vi (intransitive better insights into the difference of transitive and verb) and vt (transitive verb). -

Constructions and Result: English Phrasal Verbs As Analysed in Construction Grammar
CONSTRUCTIONS AND RESULT: ENGLISH PHRASAL VERBS AS ANALYSED IN CONSTRUCTION GRAMMAR by ANNA L. OLSON A THESIS SUBMITTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF MASTER OF ARTS in THE FACULTY OF GRADUATE STUDIES Master of Arts in Linguistics, Analytical Stream We accept this thesis as conforming to the required standard ............................................................................... Dr. Emma Pavey, PhD; Thesis Supervisor ................................................................................ Dr. Sean Allison, Ph.D.; Second Reader ................................................................................ Dr. David Weber, Ph.D.; External Examiner TRINITY WESTERN UNIVERSITY September 2013 © Anna L. Olson i Abstract This thesis explores the difference between separable and non-separable transitive English phrasal verbs, focusing on finding a reason for the non-separable verbs’ lack of compatibility with the word order alternation which is present with the separable phrasal verbs. The analysis is formed from a synthesis of ideas based on the work of Bolinger (1971) and Gorlach (2004). A simplified version of Cognitive Construction Grammar is used to analyse and categorize the phrasal verb constructions. The results indicate that separable and non-separable transitive English phrasal verbs are similar but different constructions with specific syntactic reasons for the incompatibility of the word order alternation with the non-separable verbs. ii Table of Contents Abstract ........................................................................................................................................... -

A Verb Expresses Action Or a State of Being. Verbs Are Classified in 3 Ways
Verbs A verb expresses action or a state of being. Verbs are classified in 3 ways: As helping or main verbs As action or linking verbs As transitive or intransitive verbs 1. Main Verbs and Helping Verbs A helping verb may be separated from the main verb. A verb phrase consists of one main verb and one or more helping verbs. Examples I am reading Gulliver’s Travels. We should have been listening instead of talking. Did she paint the house? Commonly Used Helping Verbs Forms of BE A modal is an auxiliary am, is, are, was, were, verb that is used to be, being, been express an attitude toward the action or state of being of the Forms of HAVE main verb. have, having, has, had MODALS can, could, may, might, Forms of DO must, ought, shall, do, does, did should, will, would Not and the contraction of n’t are never part of a verb phrase Instead, they are adverbs telling to what extent. We did not hear you. We didn’t hear you. 2. Action Verbs and Linking Verbs An action verb expresses either physical or mental activity. A linking verb connects the subject to a word or word group that identifies or describes the subject. Such a word group is called a subject complement. Commonly Used Linking Verbs Forms of Be be were shall have been should be being shall be will have been would be am will be can be could be is has been may be should have been are have been might be would have been was had been must be could have been Other Linking Verbs appear feel look seem sound taste become grow remain smell stay turn Depending on how these words are used in a sentence, they can be classified as linking or action verbs. -

Transitive & Intransitive Verbs
Transitive & Intransitive verbs Name__________________________________________________________________ Period________ There are two kinds of action verbs: transitive and intransitive. A transitive verb has a direct object. EXAMPLE: Columbus discovered America. An intransitive verb does not need an object to complete its meaning. EXAMPLES: The wind howled. He is afraid. Underline the predicate twice, and classify it as transitive or intransitive in the blank space. Find the direct object(s) in each transitive sentence and circle it. 1. Leroy paid the extremely high cellular phone bill as my birthday present. TRANSITIVE_____ 2. Ornithology is the study of various types of birds. ___________________________ 3. Move those big purple blocks that are in my way, now! ___________________________ 4. Everyone listened carefully to the talkative teacher. ___________________________ 5. The tired workers wore special uniforms to work at the concert. ___________________________ 6. We built a barbecue pit in our backyard to celebrate my birthday. ___________________________ 7. What is the name of this hanging picture? ___________________________ 8. He lives in Germany by a beautiful sparkling lake. ___________________________ 9. Who elected the principal of Campbell High School? ___________________________ 10. We walked into the brand new school for the first time. ___________________________ 11. We send many good customers to them to buy weave. ___________________________ 12. London is the foggy capital city of Great Britain. ___________________________ 13. Frank drew many excellent cartoons to make fun of his math teacher. ___________________________ 14. We study hard for the Spanish tests in Mrs. Torres’s class. ___________________________ 15. The frightened children cried loudly when they saw the monster in the closet. ___________________________ 16. Lora made this awesome poster for her project in Mr. -

Complementation in Japhug Gyalrong Guillaume Jacques
Complementation in Japhug Gyalrong Guillaume Jacques To cite this version: Guillaume Jacques. Complementation in Japhug Gyalrong. Linguistics of the Tibeto-Burman Area, Dept. of Linguistics, University of California, 2016, 39 (2), pp.222-281 10.1075/ltba.39.2.02jac. halshs-01566124 HAL Id: halshs-01566124 https://halshs.archives-ouvertes.fr/halshs-01566124 Submitted on 20 Jul 2017 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Complementation in Japhug Gyalrong* Guillaume Jacques July 20, 2017 Jacques, Guillaume 2016. Complementation in Japhug, Linguistics of the Tibeto-Burman Area, 39(2):222–281. Abstract: This article provides a detailed survey of complement clauses and complementation strategies in Japhug. It shows the bewildering diver- sity of constructions attested in these languages, which are largely unpre- dictable and need to be specified for each complement-taking verb. Special focus is given to typologically unusual constructions, in particular Hybrid Indirect Speech. Keywords: Japhug; Reported Speech; Complement clauses; Infinitive; Participle; Serial Verb Constructions; Causative; Motion Verbs Introduction Japhug, like other Gyalrong languages, has a complex verbal morphology and a rich array of complement clauses. Building on previous research, in particular Jacques (2008, 337-356) and Sun (2012), this article presents a detailed survey of all known types of complement clauses in Japhug and their distribution among complement-taking verbs. -

Native Arabic Writers in an L2 English Jon Cotner St Cloud State University, [email protected]
Linguistic Portfolios Volume 6 Article 11 2017 Person Resolution Agreement in L2 Compositions: Native Arabic Writers in an L2 English Jon Cotner St Cloud State University, [email protected] Follow this and additional works at: https://repository.stcloudstate.edu/stcloud_ling Part of the Applied Linguistics Commons Recommended Citation Cotner, Jon (2017) "Person Resolution Agreement in L2 Compositions: Native Arabic Writers in an L2 English," Linguistic Portfolios: Vol. 6 , Article 11. Available at: https://repository.stcloudstate.edu/stcloud_ling/vol6/iss1/11 This Article is brought to you for free and open access by theRepository at St. Cloud State. It has been accepted for inclusion in Linguistic Portfolios by an authorized editor of theRepository at St. Cloud State. For more information, please contact [email protected]. Cotner: Person Resolution Agreement in L2 Compositions: Native Arabic Wri Linguistic Portfolios–ISSN 2472-5102 –Volume 6, 2017 | 125 PERSON RESOLUTION AGREEMENT IN L2 COMPOSITIONS: NATIVE ARABIC WRITERS IN AN L2 ENGLISH JON COTNER ABSTRACT Resolution rules are syntactic parameters that regulate the proper agreement of phi-features (person, number, and gender) between a noun/noun phrase and a verb phrase within a grammatical language system. One of the facets of the primary study, of which this paper is an excerpt, examines L2 English compositions written by native Arabic speakers and investigates whether students transfer person phi-feature agreement patterns from their L1 to their L2. The findings discussed in this paper reveal agreement errors in the application of person resolution rules, and the majority of these person agreement errors are found in indefinite pronoun constructions. -

Animacy in Two Chinantec Variants
SIL-Mexico Branch Electronic Working Papers #007: Animacy in Two Chinantec Variants James E. Rupp Rupp, James E. 2009. Animacy in Two Chinantec Variants. SIL-Mexico Branch Electronic Working Papers #007. [http://mexico.sil.org/resources/archives/10699] (©) SIL International. These working papers may be periodically up- dated, expanded, or corrected. Comments may be sent to the author at: [email protected]. 2 Animacy in Two Chinantec Variants Contents Abstract . 3 1 A general description of animacy . 3 1.1 Special nouns regarded as animate . 4 1.2 Part versus whole relationships . 5 2 Person marking and animacy . 6 2.1 Pronominal suffixes . 6 2.2 Obligatorily possessed nouns . 7 3 Concord agreement in the noun phrase . 8 3.1 Adjectives which precede the noun . 8 3.2 Adjectives which follow the noun . 9 3.2.1 Qualitative adjectives . 9 3.2.2 Demonstrative adjectives and the relative pronouns . 10 3.2.3 Possessive adjectives . 12 4 Verbal marking for animacy . 13 4.1 Animacy and intransitive verbs . 13 4.2 Animacy and transitive verbs . 14 4.3 Transformation of transitive verbs . 15 5 Conclusion . 16 Abbreviations . 17 Tone marking . 17 Orthography . 18 References . 19 A general description of animacy 3 Abstract This paper describes the marking for animacy in two varieties of Chinantec, Lealao and Ozu- macín. Concord agreement for animacy is required throughout the nominal phrase. In addition, the verb is marked for animacy of its arguments following an ergative-absolutive system. 1 A general description of animacy Lealao and Ozumacín are two Chinantec towns that lie in the northeastern part of the state of Oaxaca in southern Mexico. -

Alternations in Murui: a Morphological Approach Amy Ruth Havlicek
University of North Dakota UND Scholarly Commons Theses and Dissertations Theses, Dissertations, and Senior Projects January 2017 Alternations In Murui: A Morphological Approach Amy Ruth Havlicek Follow this and additional works at: https://commons.und.edu/theses Recommended Citation Havlicek, Amy Ruth, "Alternations In Murui: A Morphological Approach" (2017). Theses and Dissertations. 2229. https://commons.und.edu/theses/2229 This Thesis is brought to you for free and open access by the Theses, Dissertations, and Senior Projects at UND Scholarly Commons. It has been accepted for inclusion in Theses and Dissertations by an authorized administrator of UND Scholarly Commons. For more information, please contact [email protected]. ALTERNATIONS IN MURUI: A MORPHOLOGICAL APPROACH by Amy Havlicek Bachelor of Arts, Covenant College, 2009 A Thesis Submitted to the Graduate Faculty of the University of North Dakota in partial fulfillment of the requirements for the degree of Master of Arts Grand Forks, North Dakota December 2017 © 2017 Amy Havlicek ii This thesis, submitted by Amy Havlicek in partial fulfillment of the requirements for the Degree of Master of Arts from the University of North Dakota, has been read by the Faculty Advisory Committee under whom the work has been done and is hereby approved. ___________________________________________________________________ Dr. Stephen A. Marlett, Chair ___________________________________________________________________ Dr. John M. Clifton ___________________________________________________________________ -
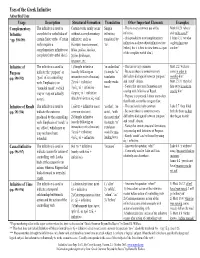
Uses of the Infinitive
Uses of the Greek Infinitive Adverbial Uses Usage Description Structural Formation Translation Other Important Elements Examples Complementary The infinitive is used to Certain verbs rarely occur Simple - This is a very common use of the Mark 10:26 ‘who is Infinitive complete the verbal idea of without a complementary infinitive, infinitive. able to be saved?’ - (It is possible to treat complementary 1 John 4:11 ‘we also *(pp. 598-599) certain finite verbs. (Certain infinitive; such as translated by verbs require a duvnamai (most common), ‘to’. infinitives as direct object infinitives (see ought to love one complementary infinitive to qevlw, mevllw, ojfeivlw, below), but it is best to view them as a part another’ of the complete verbal idea.) complete their verbal idea.) zhtevw, bouvlomai, a[rcomai, etc. Infinitive of The infinitive is used to 1) Simple infinitive ‘in order that’ - This use is very common. Matt. 2:2 ‘we have Purpose indicate the ‘purpose’ or (usually following an (A simple “to” - Be aware that it is sometimes very come in order to ‘goal’ of its controlling intransitive verb of motion) translation difficult to distinguish between ‘purpose’ worship him’ (pp. 590-592) tou: verb. Emphasis is on 2) + infinitive usually works and ‘result’ clauses. Matt. 27:31 ‘they led eijV tov ‘intended result’, (which 3) + infinitive here.) - Notice that structural formation may him away in order to pro;V tov overlap with Infinitive of Result. crucify him’ may or may not actually 4) + infinitive - Purpose is expressed 3 times more often (Rarely w/ w{ste or wJV + inf) occur). than Result, so try this category first.