Optimal Train Service Design in Urban Rail Transit Line with Considerations of Short-Turn Service and Train Size
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Purpose and Need Statement
Purpose and Need Statement South Halsted Bus Corridor Enhancement Project November 2018 Prepared for: Prepared by: g PAGE LEFT INTENTIONALLY BLANK d PURPOSE AND NEED STATEMENT Table of Contents Introduction 2 PURPOSE AND NEED STATEMENT Introduction The South Halsted Bus Corridor Enhancement Project was initiated by the Chicago Transit Authority (CTA) in partnership with Pace Suburban Bus to improve transit along approximately 11 miles of South Halsted Street, from the Pace Harvey Transportation Center to 79th Street. The corridor also includes segments of 79th and 95th Streets that provide connections to the CTA Red Line 79th and 95th Street Stations. For study purposes, the project area includes a half mile catchment area around the corridor as shown in Figure 1.1. The Purpose and Need Statement provides a foundation and justification for the project and is required for all projects going through the federal National Environmental Policy Act (NEPA) process.1 The South Halsted Bus Corridor serves the communities of Harvey, Phoenix, Dixmoor, Riverdale, Calumet Park, and the City of Chicago neighborhoods of West Pullman, Morgan Park, Roseland, Washington Heights, and Auburn Gresham. The project corridor aligns or intersects with multiple east-west and north-south arterial roadways, CTA and Pace bus routes, CTA and Metra rail stations, and shared-use paths. Transit improvements would complement CTA’s planned extension of the Red Line from 95th Street to 130th Street, as the preferred alignment is located a half mile or more from the Halsted Corridor. The Red Line Extension is currently undergoing the federal environmental review and planning process. The corridor is populated with mainly commercial businesses, surrounded by residential communities. -

City Commission
City of Miami City Hall 3500 Pan American Drive Miami, FL 33133 www.miamigov.com Meeting Minutes Thursday, May 14, 2015 9:00 AM REGULAR City Hall Commission Chambers City Commission Tomás Regalado, Mayor Wifredo (Willy) Gort, Chair Keon Hardemon, Vice Chair Marc David Sarnoff, Commissioner District Two Frank Carollo, Commissioner District Three Francis Suarez, Commissioner District Four Daniel J. Alfonso, City Manager Victoria Méndez, City Attorney Todd B. Hannon, City Clerk City Commission Meeting Minutes May 14, 2015 CONTENTS PR - PRESENTATIONS AND PROCLAMATIONS AM - APPROVING MINUTES MV - MAYORAL VETOES CA - CONSENT AGENDA PH - PUBLIC HEARINGS SR - SECOND READING ORDINANCES FR - FIRST READING ORDINANCES RE - RESOLUTIONS BC - BOARDS AND COMMITTEES DI - DISCUSSION ITEMS PART B PZ - PLANNING AND ZONING ITEM (S) MAYOR AND COMMISSIONERS' ITEMS M - MAYOR'S ITEMS D1 - DISTRICT 1 ITEMS D2 - DISTRICT 2 ITEMS D3 - DISTRICT 3 ITEMS D4 - DISTRICT 4 ITEMS D5 - DISTRICT 5 ITEMS City of Miami Page 2 Printed on 6/8/2015 City Commission Meeting Minutes May 14, 2015 9:00 A.M. INVOCATION AND PLEDGE OF ALLEGIANCE Present: Chair Gort, Commissioner Sarnoff, Commissioner Carollo, Commissioner Suarez and Vice Chair Hardemon On the 14th day of May 2015, the City Commission of the City of Miami, Florida, met at its regular meeting place in City Hall, 3500 Pan American Drive, Miami, Florida, in regular session. The Commission Meeting was called to order by Chair Gort at 9:04 a.m., recessed at 12:16 p.m., reconvened at 3:44 p.m., and adjourned at 8:14 p.m. Note for the Record: Commissioner Sarnoff entered the Commission chamber at 9:05 a.m., Vice Chair Hardemon entered the Commission chamber at 9:07 a.m., Commissioner Suarez entered the Commission chamber at 9:13 a.m., and Commissioner Carollo entered the Commission chamber at 9:38 a.m. -

Review of the G Line
Review of the G Line ,. July 10, 2013 NYC Transit G Line Review Executive Summary Executive Summary The attached report provides a comprehensive review of operations on the G line. Based on NYC Transit’s standard measures of On-Time Performance and Wait Assessment, the G performs well relative to the average subway line. At the same time, the G differs from other NYC Transit subway lines because the route is relatively short and never enters Manhattan, and thus serves primarily as a feeder/distributor with most riders transferring at least once before reaching their destinations. This review identifies a number of opportunities to improve operations on the G line, with recommendations chiefly intended to provide more even train headways and passenger loading, as well as to improve customer communication. Key Findings: While G ridership has grown significantly in recent years, it still remains relatively low compared to the rest of the system, and average passenger loads on the G are within service guidelines during both peak and off-peak hours. Scheduling the G train around the busier and more frequent F train causes uneven headways and passenger loads on the G, most significantly during the afternoon peak period, when G service is scheduled at the minimum guideline frequency of 6 trains per hour (an average 10-minute headway). G riders make twice as many transfers as the average subway rider; this high transfer rate is inconvenient for customers who must wait for multiple trains. Trains shorter than the platform length cause uncertainty about where the G train stops, contributing to uneven passenger loads. -

Constructing a Routable Retrospective Transit Timetable from a Real-Time Vehicle Location Feed and GTFS
Constructing a Routable Retrospective Transit Timetable from a Real-time Vehicle Location Feed and GTFS April 27, 2017 Abstract We describe a method for retroactively improving the accuracy of a General Transit Feed Specification (GTFS) package by using a real- time vehicle location dataset provided by the transit agency. Once modified, the GTFS package contains the observed rather than the scheduled transit operations and can be used in research assessing network performance, reliability and accessibility. We offer a case study using data from the Toronto Transit Commission and find that substantial aggregate accessibility differences exist between scheduled and observed services. This 'error' in the scheduled GTFS data may have implications for many types of measurements commonly derived from GTFS data. 1 Introduction Over the last ten years, the General Transit Feed Specification (GTFS) has emerged as an industry standard for publishing data about transit operations. Data in this format has issued from more than a thousand transit agencies around the world and that data has been incorporated into just as many user- facing routing applications. GTFS data defines transit schedule information in a format that is essentially a routable spatiotemporal network graph with stops as nodes, scheduled travel between stops as edges, and estimated travel times as the cost. This not only allows people to find their way from A to B, 1 but due to the open nature of the standard, has allowed researchers to ask interesting questions and have them answered with a degree of accuracy and scope that would have been impossible before GTFS. Such questions, still very much under active research, include measures of disparities in service provision (Farber, Ritter, and Fu, 2016; Fransen et al., 2015), temporal vari- ability (Farber, Morang, and Widener, 2014), the role of relative travel times and costs in mode choice (Owen and Levinson, 2015; Salonen and Toivonen, 2013), the degree of accessibility offered by competing transit development plans (Farber and Grandez, 2016), and many others. -
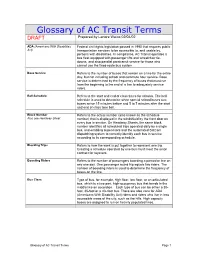
Glossary of AC Transit Terms DRAFT Prepared by Lenore Weiss 02/04/02
Glossary of AC Transit Terms DRAFT Prepared by Lenore Weiss 02/04/02 ADA (Americans With Disabilities Federal civil rights legislation passed in 1990 that requires public Act) transportation services to be accessible to, and usable by, persons with disabilities. In compliance, AC Transit operates a bus fleet equipped with passenger lifts and wheelchair tie- downs, and also parallel paratransit service for those who cannot use the fixed-route bus system. Base Service Refers to the number of buses that remain on a line for the entire day, but not including school and commute hour service. Base service is determined by the frequency of buses that must run from the beginning to the end of a line to adequately service riders. Bell Schedule Refers to the start and end of class times for schools. The bell schedule is used to determine when special school buses run; buses arrive 15 minutes before and 5 to 7 minutes after the start and end of class time bell. Block Number Refers to the actual number (also known as the schedule Also see Headway Sheet number) that is displayed in the windshield by the front door on every bus in service. On Headway Sheets, the same block number identifies all scheduled trips operated daily by a single bus, and enabling supervisors and the automated SatCom dispatching system to correctly identify each bus in service according to its corresponding schedule. Blocking Trips Refers to how the work is put together to represent one trip. Creating a schedule operated by one bus must meet the union contract for layovers. -

Optimal Design of Transit Short-Turn Trips
8 TRANSPORTATION RESEARCH RECORD 1221 Optimal Design of Transit Short-Turn Trips A VISHAI CEDER A set of procedures is presented for efficiently designing transit lines (crosstown routes, downtown-oriented routes, feeder timetables with trips that are initiated beyond the route departure routes, etc.). point, or terminated before the route arrival point, or both ("short The major objectives set forth herein are as follows: turn trips"). In practice, transit frequency is determined at the route segment with heaviest load whereas at othcl' segment · the • To identify feasible short-turn points based on passenger operation may be inefficient because of partial load (empty seats). load profile data; Transit schedulers attempt to overcome this problem by manually • To derive U1e minimum fleet size required to carry on a constructing short-turn trips to 1·cduc the number of vehicles given timetable (including the consideration of deadheading, re<auired to carry out U1e transit timetable. The study presented i.e., nonrevenue trip ); herein was meant to improve and automate thi task by identi • To adjust the number of departures at each short-turn l"ying feasible short-turn points de.riving lbe minimum fleet ize required by a given chedule, and adjusting the number of depar point to that required by the load data, provided that the tures at each short-turn point to that required by lhe load data maximum headway to be obtained is minimized (this objective (provided 'lltat the maximum headwa associated with passenger results in the maximum possible short-turn trips and the min wait lime i minimized). Other object.ives included minimizing imum required fleet size); lhe number of short-tum trip · while en uring I hat the minimum • T minimize the number f short-turn trips, provided Oect size i preserved and crcafotg vehicle schedules (blocks). -

Research Article Real-Time Integrated Limited-Stop and Short-Turning Bus Control with Stochastic Travel Time
Hindawi Journal of Advanced Transportation Volume 2017, Article ID 2960728, 9 pages https://doi.org/10.1155/2017/2960728 Research Article Real-Time Integrated Limited-Stop and Short-Turning Bus Control with Stochastic Travel Time Hu Zhang, Shuzhi Zhao, Yang Cao, Huasheng Liu, and Shidong Liang College of Transportation, Jilin University, Changchun 130022, China Correspondence should be addressed to Yang Cao; [email protected] Received 12 March 2017; Revised 20 May 2017; Accepted 6 June 2017; Published 12 July 2017 Academic Editor: Seungjae Lee Copyright © 2017 Hu Zhang et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In a traditional transit system, passenger arrival time and bus running time are typically random and uncoordinated. This randomness gives the appearance of unbalanced passenger demand and unreliable transit services. Therefore, this paper proposes a real-time control method for bus routes. In our method, buses skip some stations and turn back at appropriate stations, in order to balance passenger demand along the bus route and improve the overall transit service. Our real-time control method considers the typical changes in passenger demand and the stochastic travel time of buses. In this paper, the number of controlled vehicles at any given time is determined, and the bus holding time at the turn-back station is adopted. When implemented correctly, the optimal scheme indicates which stations should be skipped, where it is suitable for buses to turn back, and how long the holding time should be at turn-back stations, which in turn will minimize the total cost of a transit system. -

Rail Transit Capacity
7UDQVLW&DSDFLW\DQG4XDOLW\RI6HUYLFH0DQXDO PART 3 RAIL TRANSIT CAPACITY CONTENTS 1. RAIL CAPACITY BASICS ..................................................................................... 3-1 Introduction................................................................................................................. 3-1 Grouping ..................................................................................................................... 3-1 The Basics................................................................................................................... 3-2 Design versus Achievable Capacity ............................................................................ 3-3 Service Headway..................................................................................................... 3-4 Line Capacity .......................................................................................................... 3-5 Train Control Throughput....................................................................................... 3-5 Commuter Rail Throughput .................................................................................... 3-6 Station Dwells ......................................................................................................... 3-6 Train/Car Capacity...................................................................................................... 3-7 Introduction............................................................................................................. 3-7 Car Capacity........................................................................................................... -

TCQSM Part 8
Transit Capacity and Quality of Service Manual—2nd Edition PART 8 GLOSSARY This part of the manual presents definitions for the various transit terms discussed and referenced in the manual. Other important terms related to transit planning and operations are included so that this glossary can serve as a readily accessible and easily updated resource for transit applications beyond the evaluation of transit capacity and quality of service. As a result, this glossary includes local definitions and local terminology, even when these may be inconsistent with formal usage in the manual. Many systems have their own specific, historically derived, terminology: a motorman and guard on one system can be an operator and conductor on another. Modal definitions can be confusing. What is clearly light rail by definition may be termed streetcar, semi-metro, or rapid transit in a specific city. It is recommended that in these cases local usage should prevail. AADT — annual average daily ATP — automatic train protection. AADT—accessibility, transit traffic; see traffic, annual average ATS — automatic train supervision; daily. automatic train stop system. AAR — Association of ATU — Amalgamated Transit Union; see American Railroads; see union, transit. Aorganizations, Association of American Railroads. AVL — automatic vehicle location system. AASHTO — American Association of State AW0, AW1, AW2, AW3 — see car, weight Highway and Transportation Officials; see designations. organizations, American Association of State Highway and Transportation Officials. absolute block — see block, absolute. AAWDT — annual average weekday traffic; absolute permissive block — see block, see traffic, annual average weekday. absolute permissive. ABS — automatic block signal; see control acceleration — increase in velocity per unit system, automatic block signal. -

A Paratransit-Inspired Evolutionary Process for Public Transit Network Design
Andreas Neumann, Kai Nagel A paratransit-inspired evolutionary process for public transit network design Conference paper | Accepted manuscript (Postprint) This version is available at https://doi.org/10.14279/depositonce-10709 Neumann, Andreas; Nagel, Kai (2012): A paratransit-inspired evolutionary process for public transit network design. Transportation Research Board 91st Annual Meeting Terms of Use Copyright applies. A non-exclusive, non-transferable and limited right to use is granted. This document is intended solely for personal, non-commercial use. A PARATRANSIT-INSPIRED EVOLUTIONARY PROCESS FOR PUBLIC TRANSIT NET- WORK DESIGN Andreas Neumann (corresponding author) Berlin Institute of Technology Transport Systems Planning and Transport Telematics Salzufer 17-19 10587 Berlin Germany Telephone: +49 30 314 78784 FAX: +49 30 314 26269 [email protected] http://www.vsp.tu-berlin.de Kai Nagel Berlin Institute of Technology Transport Systems Planning and Transport Telematics Salzufer 17-19 10587 Berlin Germany Telephone: +49 30 314 23308 FAX: +49 30 314 26269 [email protected] http://www.vsp.tu-berlin.de Submission date: November 12, 2011 7455 words + 4 figures + 2 tables = 8955 words Abstract Public transport companies should run sustainable transit lines and demand oriented services. This paper presents an evolutionary model for the design of demand responsive routes and transport networks. The approach adopts the survival of the fittest principle from competitive developing world paratransit systems with respect to vehicles, market actor characteristics, route patterns and route functions. The model is integrated into a microscopic multi-agent simulation framework, and successfully applied to a naive and a complex scenario. -

Improving Light Rail Transit Performance in Street Operations: Toronto Case Study R.M
Improving Light Rail Transit Performance in Street Operations: Toronto Case Study R.M. Topp Planning Branch, Toronto Transit Commission Toronto, Ontario, Canada The Municipality of Metropolitan Toronto consists of were introduced in 1912. The current streetcar system six local municipalities. It covers an area of some is shown on Figure 2 and the nine routes indicated 244 mi2 and, with a population of nearly 2.5 mil represent approximately 7 percent of the 134 surface lion people, is the ninth largest city in North routes in the existing system. America. In metropolitan Toronto the streetcar network has As shown in Figure 1, the Toronto Transit Commis an east-west downtown orientation, mainly for his sion (TTC) operates 35 mi of full subway integrated toric and cost reasons. Some 119 of the 129 total within an extensive surface system and in March of streetcar route miles are centrally located within this year opened a 4-mi, elevated rapid transit the city of Toronto, with all but two of the 9 routes line. Last year the system carried about 428 million intersecting the Yonge-University-Spadina subway in revenue passengers, more than any other transit or near the central business district. These routes property in North America with the exception of the play a major two-way role in distributing subway New York Transit Authority. However, with a 1984 per patrons among local downtown destinations, as well capita rid~rship of about 200, it was second to none as feeding the Yonge-University-Spadina subway for in that category. the reverse movement. -

Reviving MILWAUKEE Through Light Rail
THE INTERNATIONAL LIGHT RAIL MAGAZINE www.lrta.org www.tautonline.com FEBRUARY 2019 NO. 974 REVIVING MILWAUKEE THROUGH LIGHT RAIL China opens two new tramways and 372km of metro Lisboa tram overturns injuring 28 Projects on hold due to TfL shortfall Ulm opens line 2 to double its tramway Sounds of silence Tram-train £4.60 Managing light rail Lessons shared from noise and vibration the UK pilot scheme “I am delighted that the UK Light Rail Conference is coming back to Greater Manchester in 2019. “Metrolink forms a key backbone of sustainable travel for the region as it continues to grow, so this important two-day event offers an invaluable chance to network with peers from around the world and share knowledge and best practice as we all aim to improve the way we plan, build and deliver exceptional light rail services to passengers.” Manchester Danny Vaughan 23-24 July 2019 head of Metrolink – transport for Greater Manchester “An excellent event, providing a stimulating and varied two-day programme addressing current The industry’s premier exhibition and knowledge-sharing and future issues pertinent to Voices event returns to Manchester for 2019! today’s light rail industry” V from the clive Pennington With unrivalled networking opportunities, this invaluable technical Director – Light rail, industry… two-day congress is well-known as the place to do amey consulting & rail business and build long-lasting relationships. There is no better place to gain true insight into the “I thought the whole conference was great – there was a workings of the sector and help shape its future.