Wind Power Plants
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Wind Turbine Foundations
IFC - ESMAP - RENEWABLE ENERGY TRAINING PROGRAM Wind Module I. Technology Overview, Market Analysis and Economics Washington DC, June 16th 2014 1 Index Wind Technology Overview, Market Analysis and Economics • Introduction and Technology Overview • Market Analysis and Perspectives • Support Schemes and Price Forecasting • Grid Integration and System Flexibility • Challenges and Competitiveness 22 Wind Power Generation Wind power generation: Conversion of wind energy into electricity using wind turbines Max Power output for a wind speed: 1 W····(,) UOE A3 v C m 2 p ͻ U= 1,225 kg/m3 ї density of the air ͻ A= swept Area ͻ V= wind Speed ͻ Cp= Power Coefficient 33 Wind - Power Coefficient Power Coefficient: Efficiency of a wind turbine transforming wind power into electricity Betz Limit: Maximum Power Coefficient of an ideal wind turbine For commercial turbines, Cp is typically between 40-50% 44 Wind - Weibull Distribution Wind speeds can be modeled using the Weibull Distribution. This function represents how often winds of different speeds will be observed at a location with a certain average wind speed. The shape of the Weibull Distribution depends on a parameter called Shape. In Northern Europe and most other locations around the world the value of Shape is approximately 2, then the distribution is named Rayleigh Distribution. 55 Wind - Capacity factor Weibull Distribution of Wind Speeds for a site with an average wind speed of 7m/s. It demonstrates visually how low and moderate winds are very common, and that strong gales are relatively rare. It is used to work out the number of hours that a certain wind speeds are likely to be recorded and the likely total energy output of a WT a year. -

Offshore Technology Yearbook
Offshore Technology Yearbook 2 O19 Generation V: power for generations Since we released our fi rst offshore direct drive turbines, we have been driven to offer our customers the best possible offshore solutions while maintaining low risk. Our SG 10.0-193 DD offshore wind turbine does this by integrating the combined knowledge of almost 30 years of industry experience. With 94 m long blades and a 10 MW capacity, it generates ~30 % more energy per year compared to its predecessor. So that together, we can provide power for generations. www.siemensgamesa.com 2 O19 20 June 2019 03 elcome to reNEWS Offshore Technology are also becoming more capable and the scope of Yearbook 2019, the fourth edition of contracts more advanced as the industry seeks to Wour comprehensive reference for the drive down costs ever further. hardware and assets required to deliver an As the growth of the offshore wind industry offshore wind farm. continues apace, so does OTY. Building on previous The offshore wind industry is undergoing growth OTYs, this 100-page edition includes a section on in every aspect of the sector and that is reflected in crew transfer vessel operators, which play a vital this latest edition of OTY. Turbines and foundations role in servicing the industry. are getting physically larger and so are the vessels As these pages document, CTVs and their used to install and service them. operators are evolving to meet the changing needs The growing geographical spread of the sector of the offshore wind development community. So is leading to new players in the fabrication space too are suppliers of installation vessels, cable-lay springing up and players in other markets entering vessels, turbines and other components. -

Offshore Wind: Can the United States Catch up with Europe? January 2016
Offshore Wind: Can the United States Catch up with Europe? January 2016 Wind energy power generation is on the rise around the world, due to its low fixed prices and lack of greenhouse gas emissions. A cumulative total of 369,553 megawatts (MW) of wind energy capacity was installed globally by the end of 2014.1 Of that total, only two percent came from offshore wind farms, which are able to capture stronger and more reliable ocean winds to generate electricity.2 Most offshore wind capacity is in Europe, where there are 3,072 grid-connected offshore wind turbines at 82 farms spanning 11 countries, for a total of 10,393.6 MW of wind energy capacity as of June 30, 2015.3 China, the leader in offshore wind in Asia, had 718.9 MW of installed capacity; Japan, 52 MW; and South Korea, 5 MW as of October 2015.4, 5, 6 In comparison, the United States is just beginning to invest in offshore wind energy, and is rapidly approaching the operational launch of its first commercial offshore wind farm. There is incredible potential for offshore wind development in the United States – the National Renewable Energy Laboratory (NREL) has estimated the United States has over 4,000 gigawatts (GW) of offshore wind potential, enough to power the country four times over.7 Installed Capacity European Union Offshore Wind Installed Capacity Offshore Wind (as of first quarter 2015) (as of first quarter 2015) Netherlands, 361 MW, 3% Sweden, 212 MW, 2% 10,393.60 Other, 60 MW, 1% Belgium, 712 MW, 7% United Kingdom, Germany, 5,017.00 2,760 MW, MW, 48% 27% 0.02 776 UNITED STATES E U R O P E A N CHINA, JAPAN, Denmark, 1,271 MW, 12% UNION SOUTH KOREA Figure 1: Megawatts of offshore wind in the world8 Figure 2: E.U. -

REPORT Wind Power in Cold Climate
Wind power in cold climate, Appendix – R&D-projects REPORT Wind Power in cold climate 5 September 2011 By: Elin Andersen, Elin Börjesson, Päivi Vainionpää & Linn Silje Undem Revised by: Christian Peterson Approved by: Eva-Britt Eklöf Assignment ref.: 10152935 Dated: 5 September 2011 Wind power in cold climate Revised: Christian Peterson Representative: Eva-Britt Eklöf Status: Final Report REPORT Wind power in cold climate Client Nordic Energy Research Stenbergsgatan 25 N-0170 Oslo NORGE Consultant WSP Environmental Box 13033 402 51 Göteborg Visitors: Rullagergatan 4 Phone: +46 31 727 25 00 Fax: +46 31 727 25 01 WSP Environment & Energy Sweden Corporate identity no.: 556057-4880 Reg. office: Stockholm www.wspgroup.se Contacts Eva-Britt Eklöf Phone: +46 31 727 28 93 Email: [email protected] 0 . 1 r e v 2 (77) Assignment ref.: 10152935 Dated: 5 September 2011 Wind power in cold climate Revised: Christian Peterson Representative: Eva-Britt Eklöf Status: Final Report Table of Contents 1 EXECUTIVESUMMARY............................................................................6 2 INTRODUCTION.....................................................................................10 2.1 Background ......................................................................................................... 10 2.2 Objectives and scope of work .............................................................................. 10 2.3 Methodology ...................................................................................................... -

Wind Energy in Sweden – Opportunities and Threats
Wind energy in Sweden – opportunities and threats Almedalen 2009 • Potential • Support system • Financial crisis • Local production The projects under construction together with smaller projects and single WTG’s are expected to contribute an additional 2 TWh of electricity before the end of 2010. Today Sweden produces 2 TWh of wind electricity, some 1.5 % of the Swedish consumption This map shows projects with all necessary permits in hand. Due to the global financial crisis, most of these projects will face a delay in terms of financial close. Almost all projects south of Lake Vänern are offshore projects and will only be built if the Government introduces a separate support system. Support system 1 Every electricity wholesaler has to show at least a certain Photovoltaic amount of these in their mix. He does this by buying certificates from the Wind power producer The amount of necessary certificates (the quota) Small hydro power rises up to 2016 Year 2016 Sweden will have 17 TWh more Bio power renewable electricity as compared to 2002 5 Support system 2 Two products to sell Electricity Price of electricity (€43/MWh) MWh Certificate Price of certificates (€30/MWh) 6 This example: €73 /MWh Wind investment in Sweden • Support system – Tradable green certificate system since 2003 • Works well and will result in 17 TWh new RES•E until 2016 – About 7 wind, 9 biomass CHP and 1 hydro • The system will be extended in time and volume to generate 25 TWh RES•E until 2020 – All of the additional 8 TWh will be wind • Required investment – Additional 13 TWh wind energy • requires about 5 000 MW installed capacity • Equals 2 500 2MW WTG’s • 7.5 billion euro The Financial Crisis • All industrial sectors are affected • Renewable energy sector will come out earlier than others. -
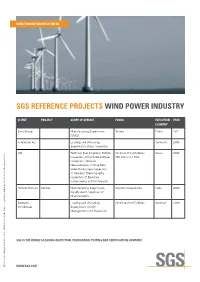
Sgs Reference Projects Wind Power Industry
WIND TURBINE MANUFACTURERS SGS REFERENCE PROJECTS WIND POWER INDUSTRY CLIENT PROJECT SCOPE OF SERVICE FOCUS EXECUTION YEAR COUNTRY Sany Group Manufacturing Supervision Towers China 2011 QA/QC Fuhrländer AG Loading and Unloading Germany 2009 Supervision, Visual Inspection NN Technical Due Diligence, Turbine Onshore Wind Turbines Korea 2009 Inspection, Wind Turbine Blade 750 kW and 2 MW Inspection, Vibration Measurement of Drive Train, Video-Endoscope Inspection of Gearbox, Thermography Inspection of Electrical Components and Oil Analysis Pioneer Wincon Various Manufacturing Supervision, Nacelle Components India 2009 Quality Audit / Approval of Manufacturers Siemens Loading and Unloading Onshore Wind Turbines Denmark 2009 Windpower Supervision, QA/QC Management and Inspection SGS IS THE WORLD’S LEADING INSPECTION, VERIFICATION, TESTING AND CERTIFICATION COMPANY. © SGS Group Management SA – 2013 – All rights reserved – SGS is a registered trademark of SGS Group Management SA WWW.SGS.COM WIND TURBINE MANUFACTURERS SGS REFERENCE PROJECTS WIND POWER INDUSTRY CLIENT PROJECT SCOPE OF SERVICE FOCUS EXECUTION YEAR COUNTRY Vestas Wind Lac Tukana Wind Regulatory Compliance Project Consultancy Kenya 2009 Systems Farm Saint Nikola Wind HSE Management and Project Consultancy Bulgaria 2009 Farm Project Supervision, Construction Supervision Various Legal Requirement Due Project Consultancy Bulgaria, 2009 Diligence Russia, Romania Gamesa Manufacturing Inspection Shafts and Flanges Korea 2008 NN Blade Inspection and NDT Wind Turbine Blades Germany 2008 Repower Vendor Assessment/ Wind Turbine Towers Korea 2008 Technical Audit Repower Vendor Assessment/ Wind Turbine Blades China, India 2008 Technical Audit WinWinD Various Manufacturing Supervision and Towers India 2008 Power Energy Final Acceptance Inspection Private Limited Design Verification Foundations Germany 2008 SGS IS THE WORLD’S LEADING INSPECTION, VERIFICATION, TESTING AND CERTIFICATION COMPANY. -

The European Offshore Wind Industry - Key Trends and Statistics 2009
Photo: Dong Energy The European offshore wind industry - key trends and statistics 2009 January 2010 The european Wind energy associaTion 1 The european offshore Wind indusTry - Key Trends and sTaTisTics 2009 Contents Executive summary 3 2009 annual market 4 Market outlook: 2010 and beyond 6 Cumulative market 6 Trends: turbines, foundations, water depth and distance to shore 9 Financing highlights and developments 11 Industry highlights and developments 12 Offshore supergrid developments 13 International opportunities 14 2 The european Wind energy associaTion Executive summary 2009 offshore wind market and outlook: • 199 wind turbines installed and grid connected totalling 577 MW during 2009, up 54% from the previous year; • Turnover in 2009 was approximately €1.5 billion, and is expected to double in 2010 to approximately €3 billion; • 1,000 MW expected to be installed during 2010, a 75% market growth compared to 2009; • 17 wind farms under construction, totaling over 3,500 MW and a further 52 wind farms have been fully consented, totaling more than 16,000 MW; • More than 100 GW of offshore wind farms currently being planned by project developers and utilities. Cumulative market: • 828 wind turbines now installed and grid connected, totaling 2,056 MW in 38 wind farms in nine European countries; • Average wind turbine size is 2.9 MW; • 65% of substructures are monopiles, 23% are gravity foundations. Trends: • The average offshore wind farm size in 2009 was 72.1 MW, up from 62.2 MW the previous year; • Average water depth of offshore wind farms installed during 2009 was 12m, 0.5m deeper than the previous year, but substantially less than the 21.8m for farms currently under construction; • Average distance to shore of offshore wind farms installed during 2009 was 14.4km, 3.9km further than the previous year, but substantially less than the 30.1km for farms currently under construction. -

Offshore Wind Power and the Challenges of Large
Offshore Wind Walt Musial Power and the Manager Offshore Wind Challenges of and Ocean Power Systems Large Scale National Renewable Energy Laboratory Deployment Inaugural Meeting of the North American Wind Energy Academy August 7th - 9th, 2012 Photo: Baltic I – Wind Plant University of Massachusetts Amherst Germany 2010 Credit: Fort Felker William E. Heronemus University of Massachusetts Circa 1973 UMass has Pioneered Offshore Wind Energy • 51 projects, 3,620 MW installed (end of 2011) • 49 in shallow water <30m • 2-5 MW upwind rotor configuration (3.8 MW ave) • 80+ meter towers on monopoles Vestas 2.0 MW Turbine Horns Rev, DK • Modular geared drivetrains • Marine technologies for at sea operation. • Submarine cable technology • Oil and gas experience essential • Capacity Factors 40% or more • Higher Cost and O&M have contributed to project risk. Alpha Ventus – RePower Siemens 2.0 MW Turbines 5-MW Turbine Middlegrunden, DK Offshore Wind Power 3 National Renewable Energy Laboratory Offshore Wind Projects Cumulative And Annual Installation; The U.K. And Denmark Account For Nearly 75% Of Capacity 1,600 4,000 1,400 3,500 1,200 3,000 (MW) (MW) 1,000 2,500 Capacity Capacity 800 2,000 Installed Installed 600 1,500 Annual Cumulative 400 1,000 200 500 ‐ ‐ 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 Offshore Wind Power 4 National Renewable Energy Laboratory Offshore Wind Projects Installed, Under Construction, and Approved 30 25,585 MW 25 20 (GW) 15 Capacity 10 3,500 MW 5 3,620 MW 0 Installed Under Construction Approved Offshore -

Globalization in the Wind Energy Industry: Contribution and Economic Impact of European Companies
Renewable Energy 134 (2019) 612e628 Contents lists available at ScienceDirect Renewable Energy journal homepage: www.elsevier.com/locate/renene Globalization in the wind energy industry: contribution and economic impact of European companies Roberto Lacal-Arantegui European Commission, Joint Research Centre, Westerduinweg 3, Petten, 1755 LE, the Netherlands article info abstract Article history: This paper explores the globalization of the wind energy industry with a focus on the contribution by Received 5 October 2017 European companies and their economic impact in the global wind energy sector. Received in revised form The global wind energy industry is nowadays a tale of two worlds, China and the rest of the world. In 23 August 2018 the last five years, China installed between 37 and 48% of the annual world market, and it is all but closed Accepted 22 October 2018 to foreign companies. Consequently, Chinese manufacturers captured between 38 and 47% of the world Available online 1 November 2018 market whereas European reached between 41 and 50%. European manufacturers led in the rest of the world, serving between 73 and 82% of that market. They localise production and supply chain in the main Keywords: fi Globalization markets (e.g. India, Brazil, US) or in countries where producing for export is cost-ef cient (e.g. China, Wind industry Mexico). Turbine manufacturers enter new markets through joint ventures, technology licensing, Wind turbine manufacturers establishing wind farm developing subsidiaries, facilitating access to finance, or by acquiring a local Developers company. Wind energy sector Manufacturers help improve the capability of their suppliers and take them to serve new markets. -

Introduction to the Community Wind Farm in Neuenkirchen
Introduction to the Community Wind Farm in Neuenkirchen Michael Krug Freie Universität Berlin Environmental Policy Research Centre WinWind Transfer Workshop – “Community Owned Wind Farms in Latvia – Possibilities and obstacles” Riga, 10 October 2019 This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement no 764717. The sole responsibility for the content of this presentation lies with its author and in no way reflects the views of the European Union. Mentoring Experts (via Skype) Reimer Schoof • Managing director of the community wind farm in Neuenkirchen Horst Leithoff • Chairman of the regional branch of the German Wind Energy Association in Schleswig-Holstein • Managing director of 4 community wind farms in the region of Northern Friesland Definition of „Community energy“ The economic and operational participation and/or ownership by citizens or members of a defined community in a renewable energy project (IRENA 2018) Source: Clean Energy Wire, Data: trend:research, AEE 2017 Key drivers of community wind farms • Supportive legal and policy framework • Before 2017: Renewable Energy Sources Act provides guaranteed minimum remuneration via feed-in tariffs and feed in premiums Low market risks and high investment security Farmers, landowners, individuals, communities and cooperatives can relatively easily access financing Operators of the community wind farm in Neuenkirchen benefit from attractive feed in premiums 2017 transition to auctioning system (→ tendency -

Deliverable 2.1: Technical and Socio-Economic Conditions
Ref. Ares(2018)5593330 - 31/10/2018 Deliverable 2.1: Technical and socio-economic conditions A literature review of social acceptance of wind energy development, and an overview of the technical, socio- economic and regulatory starting conditions in the wind energy scarce target regions Date: 29.10.18 Version V2 Summary WP 2 Name of the WP: Social acceptance analyses in target regions/communities Dissemination Public Due delivery date: 28 February 2018 level: Nature: Report Actual delivery date: 08 June 2018 Lead beneficiary: CICERO Contributing beneficiaries: All partners Lead authors: Kristin Linnerud, Stine Aakre and Merethe Dotterud Leiren Contributing authors: Freie Universität Berlin (FFU), Authors: seecon Ingenieure, ENEA, Ecoazioni, Institute of Physical Energetics (IPE), Latvian Environmental Investment Fund (LEIF), Norwegian Water Resources and Energy Directorate (NVE). Polish National Energy Conservation Agency (KAPE), ECORYS ES, ACER Document history Reviewed/Approved Version Date Submitted by Partner Date by/Partner V0 13.05.18 Stine Aakre CICERO Reviewed by FFU 24.05.18 Reviewed by IPE and V0 13.05.18 Stine Aakre CICERO 17.05.18 and 07.06.18 KAPE VI 08.06.18 Stine Aakre CICERO Reviewed by FFU 08.06.18 Reviewed & approved V2 29.10.18 Merethe D. Leiren CICERO 31.10.18 by FFU, R. Di Nucci WinWind has received funding from European Union's Horizon 2020 Research and Innovation programme under Grant Agreement Nº 764717. The sole responsibility for any errors or omissions made lies with the consortium. The content does not necessarily reflect the opinion of the European Commission. The European Commission is also not responsible for any use that may be made of the information contained therein. -

Blade Technology Innovations for Utility-Scale Turbines
Blade Technology Innovations for Utility-Scale Turbines Tom Ashwill Wind Energy Department Sandia National Laboratories* Albuquerque, NM 87185, June 2006 Introduction. Sandia National Laboratories (SNL) is developing concepts that will enable the utilization of longer blades that weigh less, are more efficient structurally and aerodynamically, and impart reduced loads to the system. Several of these concepts have been incorporated into subscale prototype blades. The description of these concepts and the results of prototype blade fabrication and testing are covered here. Growth Trends. Installed wind energy capacity both worldwide and in the U.S. has grown exponentially over the past few years. The U.S. demand for new turbines is up dramatically in large part due to the re-activation of the Production Tax Credit (PTC). The inflation-adjusted COE for wind power has fallen dramatically as well. A large part of this drop has to do with the inherent efficiencies associated with larger turbines. The physical size has grown from an average of 100 kW in 1985 to over 1.5 MW today. Figure 1 shows pictures of turbines from the top utility-scale manufacturers in 2004, GE Energy (U.S.), Gamesa (Spain), Enercon (Germany), and Vestas-NEG Micon (Denmark) (1). These turbines are typically in the 1-3 MW size range. But the current trend is a continuation of the increase in size of commercial turbines (2). Per BTM Consults (1), the following companies are planning to commercialize turbines in the 3-5 MW size range by 2007: GE, Siemens, REPower, Vestas, Nordex, Ecotecnia, Prokon Nord, ScanWind, and WINWinD.