DOCSLIB.ORG

Temperature Dependence of the Hydrophobic Interaction in Protein Folding (Hydrocarbon Model) ROBERT L

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Temperature Dependence of the Hydrophobic Interaction in Protein Folding (Hydrocarbon Model) ROBERT L Proc. Natl. Acad. Sci. USA Vol. 83, pp. 8069-8072, November 1986 Biochemistry Temperature dependence of the hydrophobic interaction in protein folding (hydrocarbon model) ROBERT L. BALDWIN Department of Biochemistry, Stanford University Medical Center, Stanford, CA 94305 Contributed by Robert L. Baldwin, July 21, 1986 ABSTRACT Accurate calorimetric data for the thermo- (4) observed that the transfer of a nonpolar compound from dynamics of transfer of six liquid hydrocarbons to water have an organic medium to H20 is characterized by a large positive been combined with solubility data to provide a model for the value of ACp. The nature of the large enthalpy change in temperature dependence of the hydrophobic interaction in unfolding at high temperatures is unknown. The reason for protein folding. The model applies at temperatures for which the intersection near 1100C in plots of the specific enthalpy the change in heat capacity (ACp) is constant. The extrapolated and entropy of unfolding is also not known. Privalov (1) value of the temperature (T) at which the entropy of transfer suggested that it must result from the properties of the (AS') reaches zero is strikingly similar (T, = 112.8°C ± 2.2C) hydrophobic interaction. for the six hydrocarbons. This rmding provides an interpreta- The purpose of this article is to show that data for the tion for the empirical relation discovered by Sturtevant: the thermodynamics of solution of liquid hydrocarbons in H20 ratio AS°/ACp measured at 25C is constant for the transfer of provide a model for the temperature dependence of the nonpolar substances from nonaqueous media to water. Con- hydrophobic interaction in protein folding. Accurate calori- stancy ofthis ratio is equivalent to Ts = constant. When applied metric data are available for the heat of solution in H20 of to protein folding, the hydrocarbon model gives estimates ofthe seven liquid hydrocarbons in the range 15'C-350C (5). The contributions ofthe hydrophobic interaction to the entropy and seven hydrocarbons show quite uniform behavior, and an enthalpy changes on unfolding and, by difference, estimates of equation of state has been given (6) that describes their the residual contributions from other sources. The major share thermodynamic properties as functions of a single variable, of the large enthalpy change observed on unfolding at high nH, the number of H atoms per molecule. I show here that a temperatures comes from the hydrophobic interaction. The hydrocarbon model based on these data provides explana- hydrophobic interaction changes from being entropy-driven at tions for some of the thermodynamic properties of protein 22°C to being enthalpy-driven at 113°C. Finally, the hydro- unfolding reactions. In particular, the hydrocarbon model carbon model predicts that plots ofthe specific entropy change predicts that the major share of the large enthalpy change on unfolding versus temperature should nearly intersect close observed on protein unfolding at high temperatures comes to 113°C, as observed by Privalov. from the hydrophobic interaction. As defined here, "hydrophobic interaction" refers to the The thermodynamic properties of the unfolding reactions of process in which a hydrophobic side chain of an unfolded globular proteins are now known accurately as a function of protein is taken out of H20 and is buried in the interior of a temperature through calorimetric studies. Many ofthese data protein through folding. When this definition is used, the have been obtained by Privalov and co-workers, and they are hydrophobic interaction can be modeled by solvent transfer summarized and analyzed by him (1). The unfolding reactions experiments, as shown originally by Kauzmann (7), and of different proteins display certain common properties. The developed by Tanford (8-11) and other workers (12, 13). The enthalpy of unfolding depends on the temperature at which solvent transfer model is open to criticism, particularly unfolding occurs, which can be varied by adjusting pH or because the interior of a protein differs in obvious respects guanidine hydrochloride concentration. The unfolding from an organic liquid (14-17). Nevertheless, following an enthalpy is small at room temperature but increases rapidly earlier analysis (18), Rose et al. (19) find a close correlation with temperature, becoming large at high temperatures. ACp, between the average extent of burial of an amino acid side the difference in heat capacity between the native and chain and its hydrophobicity on the scale of Nozaki and in the Tanford (10). The liquid transfer process is used here as a unfolded forms, is independent of temperature range semi-quantitative model for the burial of hydrophobic side studied (up to 80°C). Plots of the specific enthalpy of chains during folding, and criticisms of the model are dis- unfolding (enthalpy per g) versus temperature intersect at a cussed later. common high temperature for several globular proteins [at Transfer of a hydrocarbon from the pure liquid to H20 can 110°C, see figure 24 ofPrivalov's review (1)]. The slope ofthe be divided into two steps: (l) transfer from the liquid hydro- plot, which is ACp per g of protein, is linearly related to the carbon into the vapor phase and (ii) transfer from the vapor fraction of hydrophobic residues. These proteins also show phase into H20. Data for the second step of the transfer an approximate intersection point near 110°C when the process have been given for compounds that serve as models specific entropy of unfolding is plotted against temperature for amino acid side chains (20). When the overall process is (see figure 26 in ref. 1). analyzed theoretically (21-26), it is necessary to consider Some of these properties are understood but others are each step separately. Experimentally, the overall transfer obscure. The large and positive value of ACp is commonly process can be modeled by a single experiment, either by a attributed to the hydrophobic interaction, although other liquid partition experiment or by a solubility experiment. The factors may contribute to ACp (2, 3). As early as 1935, Edsall Abbreviations: T., temperature at which AS' = 0; Th, temperature at The publication costs ofthis article were defrayed in part by page charge which AR"= 0. (AS0 and AJ? refer to the standard-state entropy and payment. This article must therefore be hereby marked "advertisement" enthalpy changes for transfer of a hydrocarbon from the liquid in accordance with 18 U.S.C. §1734 solely to indicate this fact. hydrocarbon to H20.) 8069 Downloaded by guest on September 26, 2021 8070 Biochemistry: Baldwin Proc. Natl. Acad. Sci. USA 83 (1986) equations used to analyze these experiments are presented by which AS0 goes to zero. If T2 is taken to be Ts, the temperature Tanford (11). at which AS0 is zero, then Eq. 4 becomes Properties of the Liquid Hydrocarbon Model -A50/ACp = ln(Ts/T). [5] Thus, if T, is constant, the ratio AS/ACp is constant. The The standard Gibbs energy of transfer (per mol), AG, is temperatures at which AS0 and AR' go to zero are denoted related to the solubility X by here as T, and Th, following the notation used by Becktel and Schellman to describe the thermodynamics of folding of T4 AG' = -RT In X, [1] lysozyme mutants (J. A. Schellman, personal communica- tion). The values ofAS0, ACp, and T. are given in Table 1. The where X is the mol fraction ofhydrocarbon dissolved in H20. six liquid hydrocarbons show closely similar values of T,: The purpose of using the mol fraction scale is to avoid 386.0 K or 112.80C ± 2.40C. From Sturtevant's relation (2), including in AG' a term involving the entropy of mixing (7, obtained from data for a wide range of nonpolar compounds, 11). It has been argued that a number density scale such as one finds T, = 387.8 K or 114.60C ± 18TC. the molar scale should be used instead (27, 28). For consist- Eq. 5 can be tested with data taken at different tempera- ency with earlier work in the literature, I use the mol fraction tures. Table 2 provides such a test for benzene in H20, for scale here. Numerical examples of the change in AG' caused which the necessary solubility data (30) and calorimetric data by shifting to Ben-Naim's concentration scale have been (5) are available in the range 15'C-350C. Table 2 shows that given (26). The standard-state entropy of transfer, AS', is the same value of T, for benzene is found from data taken at obtained from different temperatures. This is not surprising, because ACp is known to be constant in this range and Eq. 5 assumes only A5 = A /T + R In X, [2] that ACp is constant. What is the meaning of a constant value of T, found for where AH? is the standard enthalpy of transfer. Data for AS0, different nonpolar substances? When AS0 is zero, the solution All0, and X at 250C are given in Table 1 for the six liquid shows ideal entropy of mixing by definition. T. is the hydrocarbons considered. [Propylbenzene, which also was temperature at which an aqueous solution of a nonpolar studied (5) is omitted here for lack of solubility data.] substance becomes a regular solution, with AS0 = 0 but with Data for seven liquid hydrocarbons show A11' to be a linear All nonzero [cf. Shinoda and Fujihira (31)]. There are function oftemperature in the range studied, 15'C-350C, with reasons for suspecting that ACp decreases at high tempera- ACp constant (5): tures (see below). In this case, T, is a hypothetical temper- ature. (In any case, T, is above the boiling point of H20.) If AI(T2) = AI(T1) + ACp(T2 - T1). [31 ACp decreases at high temperatures, then T, is the temper- ature at which AS0 would go to zero ifthe solution obeyed the When ACp is nonzero, AS0 like ARmust be a function of ACp same rules at high temperatures as in the range for which ACp and temperature.
Load more

Recommended publications
  • Heterogeneous Impacts of Protein-Stabilizing Osmolytes On
    bioRxiv preprint doi: https://doi.org/10.1101/328922; this version posted May 23, 2018. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC-ND 4.0 International license. Heterogeneous Impacts of Protein-Stabilizing Osmolytes on Hydrophobic Interaction Mrinmoy Mukherjee and Jagannath Mondal⇤ Tata Institute of Fundamental Research Hyderabad, 500107 India E-mail: [email protected],+914020203091 Abstract Osmolytes’ mechanism of protecting proteins against denaturation is a longstanding puzzle, further complicated by the complex diversities inherent in protein sequences. An emergent approach in understanding osmolytes’ mechanism of action towards biopoly- mer has been to investigate osmolytes’ interplay with hydrophobic interaction, the ma- jor driving force of protein folding. However, the crucial question is whether all these protein-stabilizing osmolytes display a single unified mechanism towards hydrophobic interactions. By simulating the hydrophobic collapse of a macromolecule in aqueous solutions of two such osmoprotectants, Glycine and Trimethyl N-oxide (TMAO), both of which are known to stabilize protein’s folded conformation, we here demonstrate that these two osmolytes can impart mutually contrasting effects towards hydropho- bic interaction. While TMAO preserves its protectant nature across diverse range of polymer-osmolyte interactions, glycine is found to display an interesting cross-over from being a protectant at weaker polymer-osmolyte interaction to a denaturant of hydrophobicity at stronger polymer-osmolyte interactions. A preferential-interaction analysis reveals that a subtle balance of conformation-dependent exclusion/binding of ⇤To whom correspondence should be addressed 1 bioRxiv preprint doi: https://doi.org/10.1101/328922; this version posted May 23, 2018.
    [Show full text]
  • Protein Structure & Folding
    6 Protein Structure & Folding To understand protein folding In the last chapter we learned that proteins are composed of amino acids Goal as a chemical equilibrium. linked together by peptide bonds. We also learned that the twenty amino acids display a wide range of chemical properties. In this chapter we will see Objectives that how a protein folds is determined by its amino acid sequence and that the three-dimensional shape of a folded protein determines its function by After this chapter, you should be able to: the way it positions these amino acids. Finally, we will see that proteins fold • describe the four levels of protein because doing so minimizes Gibbs free energy and that this minimization structure and the thermodynamic involves both making the most favorable bonds and maximizing disorder. forces that stabilize them. • explain how entropy (S) and enthalpy Proteins exhibit four levels of structure (H) contribute to Gibbs free energy. • use the equation ΔG = ΔH – TΔS The structure of proteins can be broken down into four levels of to determine the dependence of organization. The first is primary structure, the linear sequence of amino the favorability of a reaction on acids in the polypeptide chain. By convention, the primary sequence is temperature. written in order from the amino acid at the N-terminus (by convention • explain the hydrophobic effect and its usually on the left) to the amino acid at the C-terminus. The second level role in protein folding. of protein structure, secondary structure, is the local conformation adopted by stretches of contiguous amino acids.
    [Show full text]
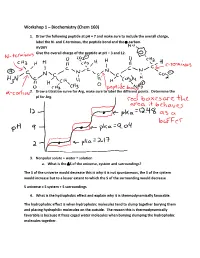
  • Workshop 1 – Biochemistry (Chem 160)
    Workshop 1 – Biochemistry (Chem 160) 1. Draw the following peptide at pH = 7 and make sure to include the overall charge, label the N- and C-terminus, the peptide bond and the -carbon. AVDKY Give the overall charge of the peptide at pH = 3 and 12. 2. Draw a titration curve for Arg, make sure to label the different points. Determine the pI for Arg. 3. Nonpolar solute + water = solution a. What is the S of the universe, system and surroundings? The S of the universe would decrease this is why it is not spontaneous, the S of the system would increase but to a lesser extent to which the S of the surrounding would decrease S universe = S system + S surroundings 4. What is the hydrophobic effect and explain why it is thermodynamically favorable. The hydrophobic effect is when hydrophobic molecules tend to clump together burying them and placing hydrophilic molecules on the outside. The reason this is thermodynamically favorable is because it frees caged water molecules when burying clumping the hydrophobic molecules together. 5. Urea dissolves very readily in water, but the solution becomes very cold as the urea dissolves. How is this possible? Urea dissolves in water because when dissolving there is a net increase in entropy of the universe. The heat exchange, getting colder only reflects the enthalpy (H) component of the total energy change. The entropy change is high enough to offset the enthalpy component and to add up to an overall -G 6. A mutation that changes an alanine residue in the interior of a protein to valine is found to lead to a loss of activity.
    [Show full text]
  • Solubility and Aggregation of Selected Proteins Interpreted on the Basis of Hydrophobicity Distribution
    International Journal of Molecular Sciences Article Solubility and Aggregation of Selected Proteins Interpreted on the Basis of Hydrophobicity Distribution Magdalena Ptak-Kaczor 1,2, Mateusz Banach 1 , Katarzyna Stapor 3 , Piotr Fabian 3 , Leszek Konieczny 4 and Irena Roterman 1,2,* 1 Department of Bioinformatics and Telemedicine, Jagiellonian University—Medical College, Medyczna 7, 30-688 Kraków, Poland; [email protected] (M.P.-K.); [email protected] (M.B.) 2 Faculty of Physics, Astronomy and Applied Computer Science, Jagiellonian University, Łojasiewicza 11, 30-348 Kraków, Poland 3 Institute of Computer Science, Silesian University of Technology, Akademicka 16, 44-100 Gliwice, Poland; [email protected] (K.S.); [email protected] (P.F.) 4 Chair of Medical Biochemistry—Jagiellonian University—Medical College, Kopernika 7, 31-034 Kraków, Poland; [email protected] * Correspondence: [email protected] Abstract: Protein solubility is based on the compatibility of the specific protein surface with the polar aquatic environment. The exposure of polar residues to the protein surface promotes the protein’s solubility in the polar environment. The aquatic environment also influences the folding process by favoring the centralization of hydrophobic residues with the simultaneous exposure to polar residues. The degree of compatibility of the residue distribution, with the model of the concentration of hydrophobic residues in the center of the molecule, with the simultaneous exposure of polar residues is determined by the sequence of amino acids in the chain. The fuzzy oil drop model enables the quantification of the degree of compatibility of the hydrophobicity distribution Citation: Ptak-Kaczor, M.; Banach, M.; Stapor, K.; Fabian, P.; Konieczny, observed in the protein to a form fully consistent with the Gaussian 3D function, which expresses L.; Roterman, I.
    [Show full text]
  • Solubility & Density
    Natural Resources - Water WHAT’S SO SPECIAL ABOUT WATER: SOLUBILITY & DENSITY Activity Plan – Science Series ACTpa025 BACKGROUND Project Skills: Water is able to “dissolve” other substances. The molecules of water attract and • Discovery of chemical associate with the molecules of the substance that dissolves in it. Youth will have fun and physical properties discovering and using their critical thinking to determine why water can dissolve some of water. things and not others. Life Skills: • Critical thinking – Key vocabulary words: develops wider • Solvent is a substance that dissolves other substances, thus forming a solution. comprehension, has Water dissolves more substances than any other and is known as the “universal capacity to consider solvent.” more information • Density is a term to describe thickness of consistency or impenetrability. The scientific formula to determine density is mass divided by volume. Science Skills: • Hypothesis is an explanation for a set of facts that can be tested. (American • Making hypotheses Heritage Dictionary) • The atom is the smallest unit of matter that can take part in a chemical reaction. Academic Standards: It is the building block of matter. The activity complements • A molecule consists of two or more atoms chemically bonded together. this academic standard: • Science C.4.2. Use the WHAT TO DO science content being Activity: Density learned to ask questions, 1. Take a clear jar, add ¼ cup colored water, ¼ cup vegetable oil, and ¼ cup dark plan investigations, corn syrup slowly. Dark corn syrup is preferable to light so that it can easily be make observations, make distinguished from the oil. predictions and offer 2.
    [Show full text]
  • THE SOLUBILITY of GASES in LIQUIDS Introductory Information C
    THE SOLUBILITY OF GASES IN LIQUIDS Introductory Information C. L. Young, R. Battino, and H. L. Clever INTRODUCTION The Solubility Data Project aims to make a comprehensive search of the literature for data on the solubility of gases, liquids and solids in liquids. Data of suitable accuracy are compiled into data sheets set out in a uniform format. The data for each system are evaluated and where data of sufficient accuracy are available values are recommended and in some cases a smoothing equation is given to represent the variation of solubility with pressure and/or temperature. A text giving an evaluation and recommended values and the compiled data sheets are published on consecutive pages. The following paper by E. Wilhelm gives a rigorous thermodynamic treatment on the solubility of gases in liquids. DEFINITION OF GAS SOLUBILITY The distinction between vapor-liquid equilibria and the solubility of gases in liquids is arbitrary. It is generally accepted that the equilibrium set up at 300K between a typical gas such as argon and a liquid such as water is gas-liquid solubility whereas the equilibrium set up between hexane and cyclohexane at 350K is an example of vapor-liquid equilibrium. However, the distinction between gas-liquid solubility and vapor-liquid equilibrium is often not so clear. The equilibria set up between methane and propane above the critical temperature of methane and below the criti­ cal temperature of propane may be classed as vapor-liquid equilibrium or as gas-liquid solubility depending on the particular range of pressure considered and the particular worker concerned.
    [Show full text]
  • Hydrophobic Effect, Water Structure, and Heat Capacity Changes
    J. Phys. Chem. B 1997, 101, 4343-4348 4343 Hydrophobic Effect, Water Structure, and Heat Capacity Changes Kim A. Sharp* and Bhupinder Madan Department of Biochemistry & Biophysics, UniVersity of PennsylVania, 3700 Hamilton Walk, Philadelphia, PennsylVania 19104-6059 ReceiVed: January 16, 1997; In Final Form: April 1, 1997X hyd The hydration heat capacity (∆Cp ) of nine solutes of varying hydrophobicity was studied using a combination of a random network model equation of water and Monte Carlo simulations. Nonpolar solutes cause a concerted decrease in the average length and angle of the water-water hydrogen bonds in the first hydration shell, while polar and ionic solutes have the opposite effect. This is due to changes in the amounts, relative to bulk water, of two populations of hydrogen bonds: one with shorter and more linear bonds and the other with longer and more bent bonds. Heat capacity changes were calculated from these changes in water structure using a random network model equation of state. The calculated changes account for observed hyd differences in ∆Cp for the various solutes. The simulations provide a unified picture of hydrophobic and hyd polar hydration, and both a structural and thermodynamic explanation of the opposite signs of ∆Cp observed for polar and nonpolar solutes. Introduction nonpolar groups means that at higher temperatures (T > 80 °C) their insolubility results from unfavorable changes in enthalpy, In recent years analysis of heat capacity changes has become not entropy. Second, the hydration of a majority of polar and of central importance in understanding the thermodynamics of ionic solutes is also accompanied by a decrease in entropy, and protein folding, protein-protein binding, protein-nucleic acid thus by some kind of structuring of water, but in this case binding, and the hydrophobic effect.1-7 There are several hyd 7,16-20 reasons for this.
    [Show full text]
  • Carbon Dioxide Capture by Chemical Absorption: a Solvent Comparison Study
    Carbon Dioxide Capture by Chemical Absorption: A Solvent Comparison Study by Anusha Kothandaraman B. Chem. Eng. Institute of Chemical Technology, University of Mumbai, 2005 M.S. Chemical Engineering Practice Massachusetts Institute of Technology, 2006 SUBMITTED TO THE DEPARTMENT OF CHEMICAL ENGINEERING IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY IN CHEMICAL ENGINEERING PRACTICE AT THE MASSACHUSETTS INSTITUTE OF TECHNOLOGY JUNE 2010 © 2010 Massachusetts Institute of Technology All rights reserved. Signature of Author……………………………………………………………………………………… Department of Chemical Engineering May 20, 2010 Certified by……………………………………………………….………………………………… Gregory J. McRae Hoyt C. Hottel Professor of Chemical Engineering Thesis Supervisor Accepted by……………………………………………………………………………….................... William M. Deen Carbon P. Dubbs Professor of Chemical Engineering Chairman, Committee for Graduate Students 1 2 Carbon Dioxide Capture by Chemical Absorption: A Solvent Comparison Study by Anusha Kothandaraman Submitted to the Department of Chemical Engineering on May 20, 2010 in partial fulfillment of the requirements of the Degree of Doctor of Philosophy in Chemical Engineering Practice Abstract In the light of increasing fears about climate change, greenhouse gas mitigation technologies have assumed growing importance. In the United States, energy related CO2 emissions accounted for 98% of the total emissions in 2007 with electricity generation accounting for 40% of the total1. Carbon capture and sequestration (CCS) is one of the options that can enable the utilization of fossil fuels with lower CO2 emissions. Of the different technologies for CO2 capture, capture of CO2 by chemical absorption is the technology that is closest to commercialization. While a number of different solvents for use in chemical absorption of CO2 have been proposed, a systematic comparison of performance of different solvents has not been performed and claims on the performance of different solvents vary widely.
    [Show full text]
  • THE SOLUBILITY of GASES in LIQUIDS INTRODUCTION the Solubility Data Project Aims to Make a Comprehensive Search of the Lit- Erat
    THE SOLUBILITY OF GASES IN LIQUIDS R. Battino, H. L. Clever and C. L. Young INTRODUCTION The Solubility Data Project aims to make a comprehensive search of the lit­ erature for data on the solubility of gases, liquids and solids in liquids. Data of suitable accuracy are compiled into data sheets set out in a uni­ form format. The data for each system are evaluated and where data of suf­ ficient accuracy are available values recommended and in some cases a smoothing equation suggested to represent the variation of solubility with pressure and/or temperature. A text giving an evaluation and recommended values and the compiled data sheets are pUblished on consecutive pages. DEFINITION OF GAS SOLUBILITY The distinction between vapor-liquid equilibria and the solUbility of gases in liquids is arbitrary. It is generally accepted that the equilibrium set up at 300K between a typical gas such as argon and a liquid such as water is gas liquid solubility whereas the equilibrium set up between hexane and cyclohexane at 350K is an example of vapor-liquid equilibrium. However, the distinction between gas-liquid solUbility and vapor-liquid equilibrium is often not so clear. The equilibria set up between methane and propane above the critical temperature of methane and below the critical temperature of propane may be classed as vapor-liquid equilibrium or as gas-liquid solu­ bility depending on the particular range of pressure considered and the par­ ticular worker concerned. The difficulty partly stems from our inability to rigorously distinguish between a gas, a vapor, and a liquid, which has been discussed in numerous textbooks.
    [Show full text]
  • Biotransformation: Basic Concepts (1)
    Chapter 5 Absorption, Distribution, Metabolism, and Elimination of Toxics Biotransformation: Basic Concepts (1) • Renal excretion of chemicals Biotransformation: Basic Concepts (2) • Biological basis for xenobiotic metabolism: – To convert lipid-soluble, non-polar, non-excretable forms of chemicals to water-soluble, polar forms that are excretable in bile and urine. – The transformation process may take place as a result of the interaction of the toxic substance with enzymes found primarily in the cell endoplasmic reticulum, cytoplasm, and mitochondria. – The liver is the primary organ where biotransformation occurs. Biotransformation: Basic Concepts (3) Biotransformation: Basic Concepts (4) • Interaction with these enzymes may change the toxicant to either a less or a more toxic form. • Generally, biotransformation occurs in two phases. – Phase I involves catabolic reactions that break down the toxicant into various components. • Catabolic reactions include oxidation, reduction, and hydrolysis. – Oxidation occurs when a molecule combines with oxygen, loses hydrogen, or loses one or more electrons. – Reduction occurs when a molecule combines with hydrogen, loses oxygen, or gains one or more electrons. – Hydrolysis is the process in which a chemical compound is split into smaller molecules by reacting with water. • In most cases these reactions make the chemical less toxic, more water soluble, and easier to excrete. Biotransformation: Basic Concepts (5) – Phase II reactions involves the binding of molecules to either the original toxic molecule or the toxic molecule metabolite derived from the Phase I reactions. The final product is usually water soluble and, therefore, easier to excrete from the body. • Phase II reactions include glucuronidation, sulfation, acetylation, methylation, conjugation with glutathione, and conjugation with amino acids (such as glycine, taurine, and glutamic acid).
    [Show full text]
  • Design Guidelines for Carbon Dioxide Scrubbers I
    "NCSCTECH MAN 4110-1-83 I (REVISION A) S00 TECHNICAL MANUAL tow DESIGN GUIDELINES FOR CARBON DIOXIDE SCRUBBERS I MAY 1983 REVISED JULY 1985 Prepared by M. L. NUCKOLS, A. PURER, G. A. DEASON I OF * Approved for public release; , J 1"73 distribution unlimited NAVAL COASTAL SYSTEMS CENTER PANAMA CITY, FLORIDA 32407 85. .U 15 (O SECURITY CLASSIFICATION OF TNIS PAGE (When Data Entered) R O DOCULMENTATIONkB PAGE READ INSTRUCTIONS REPORT DOCUMENTATION~ PAGE BEFORE COMPLETING FORM 1. REPORT NUMBER 2a. GOVT AQCMCSION N (.SAECIP F.NTTSChALOG NUMBER "NCSC TECHMAN 4110-1-83 (Rev A) A, -NI ' 4. TITLE (and Subtitle) S. TYPE OF REPORT & PERIOD COVERED "Design Guidelines for Carbon Dioxide Scrubbers '" 6. PERFORMING ORG. REPORT N UMBER A' 7. AUTHOR(&) 8. CONTRACT OR GRANT NUMBER(S) M. L. Nuckols, A. Purer, and G. A. Deason 9. PERFORMING ORGANIZATION NAME AND ADDRESS 10. PROGRAM ELEMENT, PROJECT. TASK AREA 6t WORK UNIT NUMBERS Naval Coastal PanaaLSystems 3407Project CenterCty, S0394, Task Area Panama City, FL 32407210,WrUnt2 22102, Work Unit 02 II. CONTROLLING OFFICE NAME AND ADDRE1S t2. REPORT 3ATE May 1983 Rev. July 1985 13, NUMBER OF PAGES 69 14- MONI TORING AGENCY NAME & ADDRESS(if different from Controtling Office) 15. SECURITY CLASS. (of this report) UNCLASSIFIED ISa. OECL ASSI FICATION/DOWNGRADING _ __N•AEOULE 16. DISTRIBUTION STATEMENT (of thia Repott) Approved for public release; distribution unlimited. 17. DISTRIBUTION STATEMENT (of the abstract entered In Block 20, If different from Report) IS. SUPPLEMENTARY NOTES II. KEY WORDS (Continue on reverse side If noceassry and Identify by block number) Carbon Dioxide; Scrubbers; Absorption; Design; Life Support; Pressure; "Swimmer Diver; Environmental Effects; Diving., 20.
    [Show full text]
  • Biological Membranes
    14 Biological Membranes To understand the structure The fundamental unit of life is the cell. All living things are composed of Goal and composition of biological cells, be it a single cell in the case of many microorganisms or a highly membranes. organized ensemble of myriad cell types in the case of multicellular organisms. A defining feature of the cell is a membrane, the cytoplasmic Objectives membrane, that surrounds the cell and separates the inside of the cell, the After this chapter, you should be able to cytoplasm, from other cells and the extracellular milieu. Membranes also • distinguish between cis and trans surround specialized compartments inside of cells known as organelles. unsaturated fatty acids. Whereas cells are typically several microns (μm) in diameter (although • explain why phospholipids some cells can be much larger), the membrane is only about 10 nanometers spontaneously form lipid bilayers and (nm) thick. Yet, and as we will see in subsequent chapters, the membrane is sealed compartments. not simply an ultra-thin, pliable sheet that encases the cytoplasm. Rather, • describe membrane fluidity and how it membranes are dynamic structures that mediate many functions in the is affected by membrane composition life of the cell. In this chapter we examine the composition of membranes, and temperature. their assembly, the forces that stabilize them, and the chemical and physical • explain the role of cholesterol in properties that influence their function. buffering membrane fluidity. The preceding chapters have focused on two kinds of biological molecules, • explain how the polar backbone namely proteins and nucleic acids, that are important in the workings of a membrane protein can be accommodated in a bilayer.
    [Show full text]