DOCSLIB.ORG

Effectiveness of Cloud Services for Scientific and Vod Applications

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Effectiveness of Cloud Services for Scientific and Vod Applications University of Massachusetts Amherst ScholarWorks@UMass Amherst Doctoral Dissertations Dissertations and Theses March 2015 Effectiveness of Cloud Services for Scientific and oDV Applications Dilip Kumar Krishnappa University of Massachusetts Amherst Follow this and additional works at: https://scholarworks.umass.edu/dissertations_2 Part of the OS and Networks Commons Recommended Citation Krishnappa, Dilip Kumar, "Effectiveness of Cloud Services for Scientific and oDV Applications" (2015). Doctoral Dissertations. 310. https://doi.org/10.7275/6377319.0 https://scholarworks.umass.edu/dissertations_2/310 This Open Access Dissertation is brought to you for free and open access by the Dissertations and Theses at ScholarWorks@UMass Amherst. It has been accepted for inclusion in Doctoral Dissertations by an authorized administrator of ScholarWorks@UMass Amherst. For more information, please contact [email protected]. EFFECTIVENESS OF CLOUD SERVICES FOR SCIENTIFIC AND VOD APPLICATIONS A Dissertation Presented by DILIP KUMAR KRISHNAPPA Submitted to the Graduate School of the University of Massachusetts Amherst in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY February 2015 Electrical and Computer Engineering c Copyright by Dilip Kumar Krishnappa 2015 All Rights Reserved EFFECTIVENESS OF CLOUD SERVICES FOR SCIENTIFIC AND VOD APPLICATIONS A Dissertation Presented by DILIP KUMAR KRISHNAPPA Approved as to style and content by: Michael Zink, Chair Lixin Gao, Member David Irwin, Member Prashant Shenoy, Member Christopher V. Hollot, Department Chair Electrical and Computer Engineering To my wonderful parents, caring brother and loving sister. ACKNOWLEDGEMENTS First and foremost, I would like to thank my advisor Prof. Michael Zink. It has been an honor to be his first PhD student. For the past 5 years, he has been a constant support and guide in all my academic decisions. His mentoring and guidance has helped enjoy my stay at UMass and provided confidence to finish my PhD. I would like to thank my committee members Prof. David Irwin, Prof. Lixin Gao and Prof. Prashant Shenoy for presiding over my dissertation. I would like to thank Prof. Ramesh Sitaraman from UMass Amherst, Prof. Carsten Griwodz and Prof. P˚al Halvorsen from University of Oslo for giving me an opportunity to work with them during parts of my dissertation. I would like to thank all the reviewers and shepherds of all the conference and journal articles I have submitted during my PhD. I would like to thank my colleagues Cong Wang, Divyashri Bhat, Samamon Khemmarat and Eric Adams for working closely with me on projects related to my dissertation. My time at UMass was made enjoyable in large part due to the many friends that became a part of my life during these past 5 years. A special thanks to Ravi Vantipalli, Vikram Desai, Abhinna Jain, Satish Inampudi, Chilakam Madhusudan, Siddhartha Nalluri, Srikar Damaraju and Pavan Prakash. It is their support during all the lows and highs of being a PhD student has helped me through the past 5 years and provided moments to cherish for life. Finally, I am obliged to my grand parents, parents, my brother Amith Kumar, my sister Shruthi, my cousins Chethan and Chaitra, who have influenced me the most and were always there to support and encourage me. They have been my source of strength. I dedicate this thesis to them. v ABSTRACT EFFECTIVENESS OF CLOUD SERVICES FOR SCIENTIFIC AND VOD APPLICATIONS FEBRUARY 2015 DILIP KUMAR KRISHNAPPA B.E., VISVESWARAIAH TECHNOLOGICAL UNIVERSITY, INDIA M.S., UNIVERSITY OF MASSACHUSETTS AMHERST Ph.D., UNIVERSITY OF MASSACHUSETTS AMHERST Directed by: Professor Michael Zink Cloud platforms have emerged as the primary data warehouse for a variety of applications, such as DropBox, iCloud, Google Music, etc. These applications allow users to store data in the cloud and access it from anywhere in the world. Com- mercial clouds are also well suited for providing high-end servers for rent to execute applications that require computation resources sporadically. Cloud users only pay for the time they actually use the hardware and the amount of data that is trans- mitted to and from the cloud, which has the potential to be more cost effective than purchasing, hosting, and maintaining dedicated hardware. In this dissertation, we look into the efficiency of the cloud Infrastructure-as-a-Service (IaaS) model for two real time high bandwidth applications: A scientific application of short-term weather forecasting and Video on Demand services. vi Short-term Weather Forecasting Since today's weather forecasts only cover large regions every few hours, their use in severe weather is limited. Dedicating high-end servers for executing scientific applications that run intermittently, such as severe weather detection or generalized weather forecasting, wastes resources. In this dissertation, we present CloudCast, an application that provides short-term weather forecasts depending on user's cur- rent location. Since severe weather is rare, CloudCast leverages pay-as-you-go cloud platforms to eliminate dedicated computing infrastructure. CloudCast has two com- ponents: 1) an architecture linking weather radars to cloud resources, and 2) a Now- casting algorithm for generating accurate short-term weather forecasts. Our hypothesis is that the connectivity and diversity of current cloud platforms mitigate the impact of staging data and computation latency for Nowcasting. In evaluating our hypothesis, in this dissertation, we study CloudCast's design space, which requires significant data staging to the cloud. Short-term weather forecasting has both computational and network requirements. While it executes rarely, when- ever severe weather approaches, it benefits from an IaaS model; However, since its results are time-critical, sufficient bandwidth must be available to transmit radar data to cloud platforms before it becomes stale. In this dissertation, we analyze the networking capabilities of multiple commercial (Amazon's EC2 and Rackspace) and research (GENICloud and ExoGENI) cloud platforms for our CloudCast application. We conduct network capacity measurements between radar sites and cloud platforms throughout the country. Our results indicate that research cloud testbeds performs the best for both serial and parallel data transfer with an average throughput of 110.22 Mbps and 17.2 Mbps, respectively. We also found that the cloud services per- form better in the distributed data transfer case, where a subset of nodes transmit data in parallel to a cloud instance. The results also indicate that serial transfers vii achieve tolerable throughput, while parallel transfers represent a bottleneck for real- time weather forecasting. In addition to network capacity analysis, we also analyze the computation ca- pability of cloud services for our CloudCast application. We measure the cost and computation time to generate 15-minute forecasts for real weather data on cloud ser- vices. Also, we analyze the forecast accuracy of executing Nowcasting in the cloud using canned weather data and show high accuracy for ten minutes in the future. Fi- nally, we execute CloudCast live using an on-campus radar, and show that it delivers a 15-minute Nowcast to a mobile client in less than 2 minutes after data sampling started, which is quick enough for users and emergency management personnel to take desired action. VoD Services Advancement in Internet bandwidth connectivity to homes coupled with the stream- ing of TV shows and other media content on the Internet has led to a huge increase in VoD services in the past decade. The advent of sites such as YouTube, Hulu, Netflix, DailyMotion and various other video content providers, make it feasible for the users to share their own videos on these VoD websites or watch their favorite movies or TV shows online. The popularity of VoD services has motivated U.S national TV chan- nels such as ABC, NBC and CBS to offer their prime time programs on the Internet for users to catch up on their shows via streaming on their websites. In 2012, Internet video traffic made up 57% of the total network traffic in the Internet. This shows that with the popularity of VoD services, the amount of Internet traffic due to video increases tremendously. However, the popularity of videos offered in VoD services follow a long tail distribution, where only a few videos are highly popular and most of the videos offered are requested rarely. This long tail popularity distribution in VoD services is especially significant when content is user generated. Analysis from a YouTube trace show that, only 23% of the YouTube videos are viii requested more than once over a period of 24 hours. Consequently, 77% of the videos which are requested only once reduces the efficiency of caches deployed all around the world to serve the videos requested. Video streaming in VoD services such as Netflix, Hulu, YouTube etc., have moved from traditional streaming of a fixed bit rate video file to the client to Adaptive Bit Rate streaming (ABR). ABR streaming is realized through video streaming over HTTP where the source content is segmented into small multi-second (usually be- tween 2 and 10 seconds) segments and each segment is encoded at multiple bit rates. The process of creating multiple bit rate versions of a video is called transcoding. Once each video is transcoded into multiple bit rates, ABR streaming allows the client to choose an appropriate quality version for each video segment based on the available bandwidth between the source and client. However, long tail popularity distribution of VoD services shows that transcoding all video provided by VoD services to all the bit rates supported wastes transcoding resources and storage space. In this dissertation, we provide solutions to the issues posed by the long tail popularity distribution of VoD services. We look into the feasibility of using cloud services to reduce the traffic in the Internet by reducing the amount of video requests from the long tail distribution of VoD services. In particular, this dissertation focuses on YouTube video service, the world's most popular Internet service that hosts user- generated videos.
Load more

Recommended publications
  • Simple Statements, Large Numbers
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 7-2007 Simple Statements, Large Numbers Shana Streeks University of Nebraska-Lincoln Follow this and additional works at: https://digitalcommons.unl.edu/mathmidexppap Part of the Science and Mathematics Education Commons Streeks, Shana, "Simple Statements, Large Numbers" (2007). MAT Exam Expository Papers. 41. https://digitalcommons.unl.edu/mathmidexppap/41 This Article is brought to you for free and open access by the Math in the Middle Institute Partnership at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in MAT Exam Expository Papers by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. Master of Arts in Teaching (MAT) Masters Exam Shana Streeks In partial fulfillment of the requirements for the Master of Arts in Teaching with a Specialization in the Teaching of Middle Level Mathematics in the Department of Mathematics. Gordon Woodward, Advisor July 2007 Simple Statements, Large Numbers Shana Streeks July 2007 Page 1 Streeks Simple Statements, Large Numbers Large numbers are numbers that are significantly larger than those ordinarily used in everyday life, as defined by Wikipedia (2007). Large numbers typically refer to large positive integers, or more generally, large positive real numbers, but may also be used in other contexts. Very large numbers often occur in fields such as mathematics, cosmology, and cryptography. Sometimes people refer to numbers as being “astronomically large”. However, it is easy to mathematically define numbers that are much larger than those even in astronomy. We are familiar with the large magnitudes, such as million or billion.
    [Show full text]
  • Big Numbers Tom Davis [email protected] September 21, 2011
    Big Numbers Tom Davis [email protected] http://www.geometer.org/mathcircles September 21, 2011 1 Introduction The problem is that we tend to live among the set of puny integers and generally ignore the vast infinitude of larger ones. How trite and limiting our view! — P.D. Schumer It seems that most children at some age get interested in large numbers. “What comes after a thousand? After a million? After a billion?”, et cetera, are common questions. Obviously there is no limit; whatever number you name, a larger one can be obtained simply by adding one. But what is interesting is just how large a number can be expressed in a fairly compact way. Using the standard arithmetic operations (addition, subtraction, multiplication, division and exponentia- tion), what is the largest number you can make using three copies of the digit “9”? It’s pretty clear we should just stick to exponents, and given that, here are some possibilities: 999, 999, 9 999, and 99 . 9 9 Already we need to be a little careful with the final one: 99 . Does this mean: (99)9 or 9(9 )? Since (99)9 = 981 this interpretation would gain us very little. If this were the standard definition, then why c not write ab as abc? Because of this, a tower of exponents is always interpreted as being evaluated from d d c c c (c ) right to left. In other words, ab = a(b ), ab = a(b ), et cetera. 9 With this definition of towers of exponents, it is clear that 99 is the best we can do.
    [Show full text]
  • The Costs of Inaction
    Climate Change – the Costs of Inaction Report to Friends of the Earth England, Wales and Northern Ireland Frank Ackerman and Elizabeth Stanton Global Development and Environment Institute, Tufts University October 11, 2006 Table of Contents Executive Summary ................................................................................................. iii Introduction................................................................................................................1 Categorizing climate risks........................................................................................................... 2 The UK in 2050: hot, and getting hotter....................................................................7 Impacts of Climate Change......................................................................................11 Agriculture ................................................................................................................................ 11 Industry and infrastructure........................................................................................................ 15 Fresh water................................................................................................................................ 17 Human health............................................................................................................................ 18 Ecosystems and extinctions ...................................................................................................... 22 Summary measures of
    [Show full text]
  • What Fun! It's Practice with Scientific Notation!
    What Fun! It's Practice with Scientific Notation! Review of Scientific Notation Scientific notation provides a place to hold the zeroes that come after a whole number or before a fraction. The number 100,000,000 for example, takes up a lot of room and takes time to write out, while 108 is much more efficient. Though we think of zero as having no value, zeroes can make a number much bigger or smaller. Think about the difference between 10 dollars and 100 dollars. Even one zero can make a big difference in the value of the number. In the same way, 0.1 (one-tenth) of the US military budget is much more than 0.01 (one-hundredth) of the budget. The small number to the right of the 10 in scientific notation is called the exponent. Note that a negative exponent indicates that the number is a fraction (less than one). The line below shows the equivalent values of decimal notation (the way we write numbers usually, like "1,000 dollars") and scientific notation (103 dollars). For numbers smaller than one, the fraction is given as well. smaller bigger Fraction 1/100 1/10 Decimal notation 0.01 0.1 1 10 100 1,000 ____________________________________________________________________________ Scientific notation 10-2 10-1 100 101 102 103 Practice With Scientific Notation Write out the decimal equivalent (regular form) of the following numbers that are in scientific notation. Section A: Model: 101 = 10 1) 102 = _______________ 4) 10-2 = _________________ 2) 104 = _______________ 5) 10-5 = _________________ 3) 107 = _______________ 6) 100 = __________________ Section B: Model: 2 x 102 = 200 7) 3 x 102 = _________________ 10) 6 x 10-3 = ________________ 8) 7 x 104 = _________________ 11) 900 x 10-2 = ______________ 9) 2.4 x 103 = _______________ 12) 4 x 10-6 = _________________ Section C: Now convert from decimal form into scientific notation.
    [Show full text]
  • Ever Heard of a Prillionaire? by Carol Castellon Do You Watch the TV Show
    Ever Heard of a Prillionaire? by Carol Castellon Do you watch the TV show “Who Wants to Be a Millionaire?” hosted by Regis Philbin? Have you ever wished for a million dollars? "In today’s economy, even the millionaire doesn’t receive as much attention as the billionaire. Winners of a one-million dollar lottery find that it may not mean getting to retire, since the million is spread over 20 years (less than $3000 per month after taxes)."1 "If you count to a trillion dollars one by one at a dollar a second, you will need 31,710 years. Our government spends over three billion per day. At that rate, Washington is going through a trillion dollars in a less than one year. or about 31,708 years faster than you can count all that money!"1 I’ve heard people use names such as “zillion,” “gazillion,” “prillion,” for large numbers, and more recently I hear “Mega-Million.” It is fairly obvious that most people don’t know the correct names for large numbers. But where do we go from million? After a billion, of course, is trillion. Then comes quadrillion, quintrillion, sextillion, septillion, octillion, nonillion, and decillion. One of my favorite challenges is to have my math class continue to count by "illions" as far as they can. 6 million = 1x10 9 billion = 1x10 12 trillion = 1x10 15 quadrillion = 1x10 18 quintillion = 1x10 21 sextillion = 1x10 24 septillion = 1x10 27 octillion = 1x10 30 nonillion = 1x10 33 decillion = 1x10 36 undecillion = 1x10 39 duodecillion = 1x10 42 tredecillion = 1x10 45 quattuordecillion = 1x10 48 quindecillion = 1x10 51
    [Show full text]
  • Large Numbers from Wikipedia, the Free Encyclopedia
    Large numbers From Wikipedia, the free encyclopedia This article is about large numbers in the sense of numbers that are significantly larger than those ordinarily used in everyday life, for instance in simple counting or in monetary transactions. The term typically refers to large positive integers, or more generally, large positive real numbers, but it may also be used in other contexts. Very large numbers often occur in fields such as mathematics, cosmology, cryptography, and statistical mechanics. Sometimes people refer to numbers as being "astronomically large". However, it is easy to mathematically define numbers that are much larger even than those used in astronomy. Contents 1 Using scientific notation to handle large and small numbers 2 Large numbers in the everyday world 3 Astronomically large numbers 4 Computers and computational complexity 5 Examples 6 Systematically creating ever faster increasing sequences 7 Standardized system of writing very large numbers 7.1 Examples of numbers in numerical order 8 Comparison of base values 9 Accuracy 9.1 Accuracy for very large numbers 9.2 Approximate arithmetic for very large numbers 10 Large numbers in some noncomputable sequences 11 Infinite numbers 12 Notations 13 See also 14 Notes and references Using scientific notation to handle large and small numbers See also: scientific notation, logarithmic scale and orders of magnitude Scientific notation was created to handle the wide range of values that occur in scientific study. 1.0 × 109, for example, means one billion, a 1 followed by nine zeros: 1 000 000 000, and 1.0 × 10−9 means one billionth, or 0.000 000 001.
    [Show full text]
  • What Do the Measured Units Mean? What Is an Acceptable Measurement?
    What Do the Measured Units Mean? What is an Acceptable Measurement? Upon the adoption of the Clean Water Act in 1972 and the Safe Drinking Water Act of 1974, Federal and State agencies established standards and limits for contamination of the waters of the United States, including those used for drinking water supply. Those limits were based upon health assessments using analytical technology of the time, with many limits established at levels measured in the parts per million (ppm). As technology and research improved, Federal and State agencies occasionally adjust those limits, now measured in the parts per billion (ppb), as deemed necessary and justified by scientific review. Water professionals have the technology today to detect more substances at lower levels than ever before. As analytical methods improve, various compounds, including hexavalent chromium, are likely to be found at very low levels in many of our nation’s lakes, rivers and streams. Because units of measurement are often difficult to place into context, the following comparisons are provided: One-Part-Per-Million (mg/L or ppm) • one automobile in bumper-to-bumper traffic from Cleveland to San Francisco • one inch in 16 miles • one minute in two years • one ounce in 32 tons • one cent in $10,000 One-Part-Per-Billion (ug/L or ppb) = 1/1000 ppm • one 4-inch hamburger in a chain of hamburgers circling the earth at the equator 2.5 times • one silver dollar in a roll of silver dollars stretching from Detroit to Salt Lake City • one kernel of corn in a 45-foot high, 16-foot
    [Show full text]
  • Scientific Notation
    Scientific Methods: Scientific Notation Scientific notation is the way that scientists handle very large or very small numbers, such as the size or age of the Universe, or the size of the national debt. For example, instead of writing 1,500,000,000,000, or 1.5 trillion, we write 1.5 x 1012. There are two parts to this number: 1.5 (digits term) and 1012 (exponential term). Here are some examples of scientific notation used in astronomy (and a few just for comparison!). THE CHART OF REALLY BIG NUMBERS 1,000,000,000,000,000,000,000,000,000,000 = We don't even have a word for this. It's the 1 x 1030 mass of the Sun in kilograms. One hundred trillion billion: The 100,000,000,000,000,000,000,000 = 1 x 1023 approximate number of stars in the Universe 40.1 Trillion: the distance (in km) to the 40,100,000,000,000 = 4.01 x 1013 nearest star, Proxima Centauri. 5.7 Trillion: the number of dollars in the 1,600,000,000,000 = 5.7 x 1012 U.S. national debt, circa 2000. Two Hundred Billion: Approximate number 200,000,000,000 = 2 x 1011 of stars in the Milky Way Galaxy. 15 Billion: Approximate age of the 15,000,000,000 = 1.5 x 1010 Universe (in years). Six Billion: Approximate number of people 6,000,000,000 = 6 x 109 on the planet, circa 2000. One Billion: The number of Earth-sized 1,000,000,000 = 1 x 109 planets that would fit into the Sun; Also the speed of light in km/hr One hundred million: the radius of the Sun 100,000,000 = 1 x 108 in meters.
    [Show full text]
  • Powers of 10 & Scientific Notation
    Physics 151 Powers of 10 & Scientific Notation In all of the physical sciences, we encounter many numbers that are so large or small that it would be exceedingly cumbersome to write them with dozens of trailing or leading zeroes. Since our number system is “base-10” (based on powers of 10), it is far more convenient to write very large and very small numbers in a special exponential notation called scientific notation. In scientific notation, a number is rewritten as a simple decimal multiplied by 10 raised to some power, n, like this: x.xxxx... × 10n Powers of Ten Remember that the powers of 10 are as follows: 0 10 = 1 1 –1 1 10 = 10 10 = 0.1 = 10 2 –2 1 10 = 100 10 = 0.01 = 100 3 –3 1 10 = 1000 10 = 0.001 = 1000 4 –4 1 10 = 10,000 10 = 0.0001 = 10,000 ...and so forth. There are some important powers that we use often: 103 = 1000 = one thousand 10–3 = 0.001 = one thousandth 106 = 1,000,000 = one million 10–6 = 0.000 001 = one millionth 109 = 1,000,000,000 = one billion 10–9 = 0.000 000 001 = one billionth 1012 = 1,000,000,000,000 = one trillion 10–12 = 0.000 000 000 001 = one trillionth In the left-hand columns above, where n is positive, note that n is simply the same as the number of zeroes in the full written-out form of the number! However, in the right-hand columns where n is negative, note that |n| is one greater than the number of place-holding zeroes.
    [Show full text]
  • Removing Impediments to Sustainable Economic Development the Case of Corruption
    WPS6704 Policy Research Working Paper 6704 Public Disclosure Authorized Removing Impediments to Sustainable Economic Development Public Disclosure Authorized The Case of Corruption Augusto López Claros Public Disclosure Authorized The World Bank Public Disclosure Authorized Financial and Private Sector Development Global Indicators and Analysis Department November 2013 Policy Research Working Paper 6704 Abstract This paper examines causes and consequences of agent of resource allocation. What is the impact of corruption within the process of economic development. corruption on public finances and on the characteristics It starts by reviewing some of the factors that, over the and performance of the private sector? What distortions past couple of decades, have transformed corruption does corruption introduce in the allocation of resources from a subject on the sidelines of economic research to and in the relationships among economic agents in the a central preoccupation of policy makers and donors marketplace? The paper also addresses the question of in many countries. Drawing on a vast treasure trove of what can be done about corruption and discusses the experiences and insights accumulated during the postwar role of economic policies in developing the right sorts period and reflected in a growing body of academic of incentives and institutions to reduce the incidence research, the paper analyzes many of the institutional of corruption. Particular attention is paid to business mechanisms that sustain corruption and the impact regulation, subsidies, the budget process, international of corruption on development. This paper argues that conventions, and the role of new technologies. The paper many forms of corruption stem from the distributional concludes with some thoughts on the moral dimensions attributes of the state in its role as the economy’s central of corruption.
    [Show full text]
  • How to Measure Natural Gas?
    How to Measure Natural Gas? Describing the amount of natural gas consumed by an entire country or a single residential appliance can be confusing, since natural gas can be measured in several different ways. Quantities of natural gas are usually measured in cubic feet. CRMU lists how much gas residential customers use each month in 100 cubic feet increments or (100 cubic feet – 1 hcf). For example, a typical natural gas futures contract is a financial instrument based on the value of about 10 million cubic feet (Mmcf) of natural gas. The energy content of natural gas and other forms of energy (i.e., the potential heat that can be generated from the fuel) is measured in Btus (British thermal units). The number of "therms" that residential natural gas customers consume each month is approximately equal to hcf. Here are some frequently used units for measuring natural gas: 1 cubic foot (cf) = 1,027 Btu 100 cubic feet (1 hcf) = 1 therm (approximate) 1,000 cubic feet (1 Mcf) = 1,027,000 Btu (1 MMBtu) 1,000 cubic feet (1 Mcf) = 1 dekatherm (10 therms) 1 million (1,000,000) cubic feet (1 Mmcf) = 1,027,000,000 Btu 1 billion (1,000,000,000 cubic feet (1 bcf) = 1.027 trillion Btu 1 trillion (1,000,000,000,000) cubic feet (1Tcf) = 1.027 quadrillion Btu To put this in context: • 1,000 cubic feet of natural gas is approximately enough to meet the natural gas needs of an average home (space-heating, water-heating, cooking, etc.) for four days.
    [Show full text]
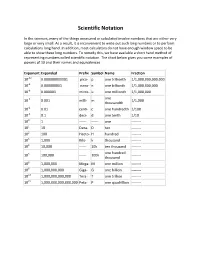
  • Scientific Notation
    Scientific Notation In the sciences, many of the things measured or calculated involve numbers that are either very large or very small. As a result, it is inconvenient to write out such long numbers or to perform calculations long hand. In addition, most calculators do not have enough window space to be able to show these long numbers. To remedy this, we have available a short hand method of representing numbers called scientific notation. The chart below gives you some examples of powers of 10 and their names and equivalences. Exponent Expanded Prefix Symbol Name Fraction 10-12 0.000000000001 pico- p one trillionth 1/1,000,000,000,000 10-9 0.000000001 nano- n one billionth 1/1,000,000,000 10-6 0.000001 micro- u one millionth 1/1,000,000 one 10-3 0.001 milli- m 1/1,000 thousandth 10-2 0.01 centi- c one hundredth 1/100 10-1 0.1 deci- d one tenth 1/10 100 1 ------ ------ one -------- 101 10 Deca- D ten -------- 102 100 Hecto- H hundred -------- 103 1,000 Kilo- k thousand -------- 104 10,000 ------ 10k ten thousand -------- one hundred 105 100,000 ------ 100k -------- thousand 106 1,000,000 Mega- M one million -------- 109 1,000,000,000 Giga- G one billion -------- 1012 1,000,000,000,000 Tera- T one trillion -------- 1015 1,000,000,000,000,000 Peta- P one quadrillion -------- Powers of 10 and Place Value.......... Multiplying by 10, 100, or 1000 in the following problems just means to add the number of zeroes to the number being multiplied.
    [Show full text]