Converting Quadratic Entropy to Diversity: Both Animals and Alleles Are Diverse, but Some Are More Diverse Than Others
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Platypus Collins, L.R
AUSTRALIAN MAMMALS BIOLOGY AND CAPTIVE MANAGEMENT Stephen Jackson © CSIRO 2003 All rights reserved. Except under the conditions described in the Australian Copyright Act 1968 and subsequent amendments, no part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, duplicating or otherwise, without the prior permission of the copyright owner. Contact CSIRO PUBLISHING for all permission requests. National Library of Australia Cataloguing-in-Publication entry Jackson, Stephen M. Australian mammals: Biology and captive management Bibliography. ISBN 0 643 06635 7. 1. Mammals – Australia. 2. Captive mammals. I. Title. 599.0994 Available from CSIRO PUBLISHING 150 Oxford Street (PO Box 1139) Collingwood VIC 3066 Australia Telephone: +61 3 9662 7666 Local call: 1300 788 000 (Australia only) Fax: +61 3 9662 7555 Email: [email protected] Web site: www.publish.csiro.au Cover photos courtesy Stephen Jackson, Esther Beaton and Nick Alexander Set in Minion and Optima Cover and text design by James Kelly Typeset by Desktop Concepts Pty Ltd Printed in Australia by Ligare REFERENCES reserved. Chapter 1 – Platypus Collins, L.R. (1973) Monotremes and Marsupials: A Reference for Zoological Institutions. Smithsonian Institution Press, rights Austin, M.A. (1997) A Practical Guide to the Successful Washington. All Handrearing of Tasmanian Marsupials. Regal Publications, Collins, G.H., Whittington, R.J. & Canfield, P.J. (1986) Melbourne. Theileria ornithorhynchi Mackerras, 1959 in the platypus, 2003. Beaven, M. (1997) Hand rearing of a juvenile platypus. Ornithorhynchus anatinus (Shaw). Journal of Wildlife Proceedings of the ASZK/ARAZPA Conference. 16–20 March. -

MORNINGTON PENINSULA BIODIVERSITY: SURVEY and RESEARCH HIGHLIGHTS Design and Editing: Linda Bester, Universal Ecology Services
MORNINGTON PENINSULA BIODIVERSITY: SURVEY AND RESEARCH HIGHLIGHTS Design and editing: Linda Bester, Universal Ecology Services. General review: Sarah Caulton. Project manager: Garrique Pergl, Mornington Peninsula Shire. Photographs: Matthew Dell, Linda Bester, Malcolm Legg, Arthur Rylah Institute (ARI), Mornington Peninsula Shire, Russell Mawson, Bruce Fuhrer, Save Tootgarook Swamp, and Celine Yap. Maps: Mornington Peninsula Shire, Arthur Rylah Institute (ARI), and Practical Ecology. Further acknowledgements: This report was produced with the assistance and input of a number of ecological consultants, state agencies and Mornington Peninsula Shire community groups. The Shire is grateful to the many people that participated in the consultations and surveys informing this report. Acknowledgement of Country: The Mornington Peninsula Shire acknowledges Aboriginal and Torres Strait Islanders as the first Australians and recognises that they have a unique relationship with the land and water. The Shire also recognises the Mornington Peninsula is home to the Boonwurrung / Bunurong, members of the Kulin Nation, who have lived here for thousands of years and who have traditional connections and responsibilities to the land on which Council meets. Data sources - This booklet summarises the results of various biodiversity reports conducted for the Mornington Peninsula Shire: • Costen, A. and South, M. (2014) Tootgarook Wetland Ecological Character Description. Mornington Peninsula Shire. • Cook, D. (2013) Flora Survey and Weed Mapping at Tootgarook Swamp Bushland Reserve. Mornington Peninsula Shire. • Dell, M.D. and Bester L.R. (2006) Management and status of Leafy Greenhood (Pterostylis cucullata) populations within Mornington Peninsula Shire. Universal Ecology Services, Victoria. • Legg, M. (2014) Vertebrate fauna assessments of seven Mornington Peninsula Shire reserves located within Tootgarook Wetland. -

An Investigation Into Factors Affecting Breeding Success in The
An investigation into factors affecting breeding success in the Tasmanian devil (Sarcophilus harrisii) Tracey Catherine Russell Faculty of Science School of Life and Environmental Science The University of Sydney Australia A thesis submitted in fulfilment of the requirements for the degree of Doctor of Philosophy 2018 Faculty of Science The University of Sydney Table of Contents Table of Figures ............................................................................................................ viii Table of Tables ................................................................................................................. x Acknowledgements .........................................................................................................xi Chapter Acknowledgements .......................................................................................... xii Abbreviations ................................................................................................................. xv An investigation into factors affecting breeding success in the Tasmanian devil (Sarcophilus harrisii) .................................................................................................. xvii Abstract ....................................................................................................................... xvii 1 Chapter One: Introduction and literature review .............................................. 1 1.1 Devil Life History ................................................................................................... -
Supporting Information
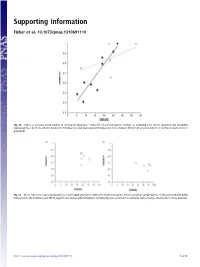
Supporting Information Fisher et al. 10.1073/pnas.1310691110 Fig. S1. Index of seasonal predictability in arthropod abundance (Colwell’s P) plotted against latitude of sampling sites where dasyurid and didelphid marsupials have been recorded in rainforest (filled points) and grassland (unfilled points). Lines indicate fitted regressions (solid line = rainforest, dashed line = grassland). Fig. S2. Mean index of seasonal predictability in arthropod abundance (Colwell’s P) plotted against mean latitude of sample points for dasyurid and didelphid marsupials in (A) shrubland and (B) Eucalypt forest and woodland habitats. Sampled species occurred in a relatively narrow range of latitudes in these habitats. Fisher et al. www.pnas.org/cgi/content/short/1310691110 1of13 Fig. S3. Phylogeny of insectivorous marsupials with known life history data, based on ref. 1 with updates from ref. 2. 1. Cardillo M, Bininda-Emonds ORP, Boakes E, Purvis A (2004) A species-level phylogenetic supertree of marsupials. J Zool 264(1):11–31. 2. Fritz SA, Bininda-Emonds ORP, Purvis A (2009) Geographical variation in predictors of mammalian extinction risk: Big is bad, but only in the tropics. Ecol Lett 12(6):538–549. Fisher et al. www.pnas.org/cgi/content/short/1310691110 2of13 Fisher et al. Table S1. Reproductive traits and diets of insectivorous marsupials Latitude (south) www.pnas.org/cgi/content/short/1310691110 Proportion Proportion Female for Habitat of of age species class for females males Male Breeding Copulation Litters Scrotal at first with species Genus species -

Submission by the Friends of Eastern Otways (Great Otway National Park
Submission by The Friends of Eastern Otways (Great Otway National Park) Incorporated [FEO (GONP)] to the Environment and Communications References Senate Committee on Faunal Extinction The FEO (GONP) is a community organisation of over 200 members whose area of operation is the Eastern area of the Great Otway National Park. The Friends carry out environmental care activities including weeding, regeneration of native vegetation and flora and fauna monitoring, in collaboration with Parks Victoria. Since 1998, FEO (GONP) has undertaken fauna monitoring in the Eastern Otways. Initially (1998 -2008) hair tubes were employed as animals enter the baited tube they leave hair samples and the animal is identified after analysis of the hair structure. More recently (2009 to 2017) remote, infra-red sensing cameras with attractants to draw native fauna to the camera sites have replaced hair tubes. With camera monitoring, the resultant images enable direct and immediate identification of a wide range of animal species. In the years since we commenced fauna monitoring we have carried out many thousands of hours of monitoring and identified many species of fauna in the area of the Eastern Otways (stretching from Point Addis in the East through Anglesea, Aireys Inlet and Lorne to Kennett River in the west, including the coastal hinterland). We make this submission to draw the committee’s attention to the decline in the number and variety of faunal species we have obtained using our monitoring methods. We would particularly wish to draw the Committee’s attention to the decline in small, native, terrestrial, mammals we have observed. Australia has many small terrestrial mammals: They are important in ecosystems such as found in GONP. -

Living with Fire: Ecology and Genetics of the Dasyurid Mammal Dasykaluta Rosamondae
Living with fire: Ecology and genetics of the dasyurid mammal Dasykaluta rosamondae Genevieve Louise Tavani Hayes Bachelor of Science (Wildlife Management) Hons This thesis is presented for the degree of Doctor of Philosophy of The University of Western Australia School of Biological Sciences 2018 Thesis Declaration I, Genevieve Louise Tavani Hayes, certify that: This thesis has been substantially accomplished during enrolment in the degree. This thesis does not contain material which has been accepted for the award of any other degree or diploma in my name, in any university or other tertiary institution. No part of this work will, in the future, be used in a submission in my name, for any other degree or diploma in any university or other tertiary institution without the prior approval of The University of Western Australia and where applicable, any partner institution responsible for the joint-award of this degree. This thesis does not contain any material previously published or written by another person, except where due reference has been made in the text. The work(s) are not in any way a violation or infringement of any copyright, trademark, patent, or other rights whatsoever of any person. The research involving animal data reported in this thesis was assessed and approved by The University of Western Australia Animal Ethics Committee. Approval #: RA/3/100/1235. The following approvals were obtained prior to commencing the relevant work described in this thesis: Health and Safety Induction, Permission to Use Animals (PUA), Program in Animal Welfare, Ethics and Science (PAWES), Department of Parks and Wildlife Regulation 4: Permission to enter DPaW lands and/or waters for the purpose of undertaking research (licence numbers: CE004035 and CE004508) and Department of Parks and Wildlife Regulation 17: Licence to take fauna for scientific purposes (licence numbers: SF009353 and SF009924). -

Nederlandse Namen Van Eierleggende Zoogdieren En
Blad1 A B C D E F G H I J K L M N O P Q 1 Nederlandse namen van Eierleggende zoogdieren en Buideldieren 2 Prototheria en Metatheria Monotremes and Marsupials Eierleggende zoogdieren en Buideldieren 3 4 Klasse Onderklasse Orde Onderorde Superfamilie Familie Onderfamilie Geslacht Soort Ondersoort Vertaling Latijnse naam Engels Frans Duits Spaans Nederlands 5 Mammalia L.: melkklier +lia Mammals Zoogdieren 6 Prototheria G.: eerste dieren Protherids Oerzoogdieren 7 Monotremata G.:één opening Monotremes Eierleggende zoogdieren 8 Tachyglossidae L: van Tachyglossus Echidnas Mierenegels 9 Zaglossus G.: door + tong Long-beaked echidnas Vachtegels 10 Zaglossus bruijnii Antonie Augustus Bruijn Western long-beaked echidna Échidné de Bruijn Langschnabeligel Equidna de hocico largo occidental Gewone vachtegel 11 Long-beaked echidna 12 Long-nosed echidna 13 Long-nosed spiny anteater 14 New Guinea long-nosed echidna 15 Zaglossus bartoni Francis Rickman Barton Eastern long-beaked echidna Échidné de Barton Barton-Langschnabeligel Equidna de hocico largo oriental Zwartharige vachtegel 16 Barton's long-beaked echidna 17 Z.b.bartoni Francis Rickman Barton Barton's long-beaked echidna Wauvachtegel 18 Z.b.clunius L.: clunius=stuit Northwestern long-beaked echidna Huonvachtegel 19 Z.b.diamondi Jared Diamond Diamond's long-beaked echidan Grootste zwartharige vachtegel 20 Z.b.smeenki Chris Smeenk Smeenk's long-beaked echidna Kleinste zwartharige vachtegel 21 Zaglossus attenboroughi David Attenborough Attenborough's long-beaked echidna Échidné d'Attenborough Attenborough-Lanschnabeligel -

The Carnivorous Marsupials
1 THE CARNIVOROUS MARSUPIALS Can you imagine a mammal that weighs as little as a Many of Earth’s species, among them carnivorous penny yet leaps five times its own height to take marsupials, have succumbed to the pressures down prey far larger than itself? If not, can you imposed by human sprawl – sent to extinction in the visualise a rapacious killer that dispatches each last few hundred years. Many more carnivorous victim with a deft bite to the neck before ripping its marsupials are under serious threat of extermination, head off? amid Earth’s sixth and first human-caused, mass How about flesh-loving devils that relentlessly extinction. pursue victims to exhaustion then simply tear them to How can we save the survivors that remain? pieces? The hunting pack squabbles over the carcass More practically perhaps, as a society, why would we in a screaming feast all night long, making enough wish to save them? racket to wake the dead. By morning, not a trace of the First, humanity must appreciate these unique and victim remains. Even its bones are ground to powder secretive animals and decide they need to be saved – by a formidable predator sporting the most powerful this requires knowledge and understanding. Without jaws for its size of any living mammal. such knowledge, we can, and will do, little or nothing What of maniacal male mammals that collectively to intervene. Recent decades are unceremoniously grab females by the neck to mate in testament to this. To ultimately save and conserve our frenzied sex sessions lasting up to 14 hours straight? precious carnivorous marsupials, then, we must first The males invariably mate themselves to death, and foremost get to know them. -

Thomas Mutton Thesis
EVOLUTIONARY BIOLOGY OF THE AUSTRALIAN CARNIVOROUS MARSUPIAL GENUS ANTECHINUS Thomas Yeshe Mutton B. App. Sci. (Hons) School of Earth, Environmental and Biological Sciences Science and Engineering Faculty Queensland University of Technology Submitted in fulfilment of the requirements for the degree of Doctor of Philosophy i Keywords Antechinus, Australia, Australian mesic zone, biogeographical barriers, biogeography, breeding biology, congeneric competition, conservation, genetic structure, Dasyuridae, dasyurid, life-history, mammal, mammalian, Miocene, molecular systematics, Phascogalini, phylogenetics, phylogeography, Pleistocene, Pliocene, population genetics, Queensland, systematics (Davison ) ii Abstract Antechinus is an Australian genus of small carnivorous marsupials. Since , the number of described species in the genus has increased by % from ten to fifteen. The systematic relationships of these new species and others in the genus have not been well resolved and a broad phylogeographic study of the genus is lacking. Moreover, little ecological information is known about these new species. Therefore, the present study examined the evolutionary biology of Antechinus in two complimentary components. The first component aimed to resolve the systematics and phylogeography of the genus Antechinus. The second component, at a finer spatiotemporal scale, aimed to improve understanding of the autecology, habitat use and risk of extinction within the group, with a focus on the recently named buff-footed antechinus, A. mysticus and a partially sympatric congener, A. subtropicus. To date, powerful (>two gene) molecular studies have only included eight Antechinus species. Here, the first comprehensive, multi-gene phylogenetic analysis of the genus using six genes was provided, incorporating all known species and subspecies of Antechinus. Four main lineages of Antechinus were reconstructed: () The dusky antechinus (A. -

Ecological Archives E082-042-A1
1 - 29 Ecological Archives E082-042-A1 http://www.esapubs.org/archive/ecol/E082/042/appendix-A.htm Diana O. Fisher, Ian P. F. Owens, and Christopher N. Johnson. 2001. The ecological basis of life history variation in marsupials. Ecology 82:3531-3540. Abensperg Traun, M., and D. Steven. 1997. Ant- and termite-eating in Australian mammals and lizards: A comparison.. Australian Journal of Ecology 22: 9-17. Algar, D. 1986. An ecological study of macropodid marsupial species on a reserve. Unpublished PhD thesis. University of Western Australia. Anderson, T. J. C., A. J. Berry, J. N. Amos, and J. M. Cook. 1988. Spool and line tracking of the New Guinea spiny bandicoot, Echymiperakalubu (Marsupialia: Peramelidae). Journal of Mammalogy 69:114-120. Aplin, K. P., and P. A. Woolley. 1993. Notes on the distribution and reproduction of the Papuan bandicoot Microperoryctes papuensis (Peroryctidae, Permelemorphia). Science in New Guinea 19:109-112. Arnold, G. W., A. Grassia, D. E. Steven, and J. R. Weeldenburg. 1991. Population ecology of western grey kangaroos in a remnant of wandoo woodland at Baker's Hill, southern Western Australia. Wildlife Research 18:561-575. Arnold, G. W., D. E. Steven, and A. Grassia. 1990. Associations between individuals and classes in groups of different size in a population of Western Grey Kangaroos, Macropus fuliginosus. Australian Wildlife Research 17:551-562. Ashworth, D. 1995. Female reproductive success and maternal investment in the Euro, Macropus robustus. Unpublished PhD thesis. University of New South Wales. Aslin, H. J. 1975. Reproduction in Antechinus maculatus Gould (Dasyuridae). Australian Wildlife Research 2:77-80. -

Conservation of Australian Insectivorous Marsupials
Conservation of Australian insectivorous marsupials: biogeography, macroecology and life history Rachael A. Collett BSc Hons A thesis submitted for the degree of Doctor of Philosophy at The University of Queensland in 2018 School of Biological Sciences ABSTRACT The insectivorous marsupial Family Dasyuridae is endemic to Australia and Papua New Guinea. Dasyurids have a variety of life history strategies and are found in a wide range of habitats, latitudes and elevations. This makes them useful for exploring life history evolution, biogeographical patterns and macroecological theory. The life history and persistence of dasyurids are thought to be tightly linked to the distribution of their arthropod prey in space and time, but we currently have a limited understanding of the mechanisms. Arthropods are declining globally, and evidence suggests that climate change is already linked to changes in arthropod availability in the northern hemisphere. Understanding the relationship between insectivorous marsupials and their arthropod prey has become particularly important, as in 2018 two species from the dasyurid genus Antechinus were federally listed as endangered, and populations of other dasyurids appear to be declining across Australia. The aim of this thesis was to combine biogeography, macroecology and life history to determine what is influencing the distribution and persistence of Australian insectivorous marsupials from the Family Dasyuridae, with a focus on antechinus species in Queensland. I addressed evolution, rarity patterns and phenological relationships between dasyurid marsupials and their arthropod prey. Chapter 2 investigated how life history traits co-vary and are related to climatic variables, specifically how the evolution of dasyurid life history is related to productivity and predictability, and how environmental drivers are linked to patterns of life history variability. -
Phascogale Calura)
Reproductive strategies of the red-tailed phascogale (Phascogale calura) Wendy Foster B.Sc. (Hons) Department of Ecology and Evolutionary Biology School of Earth and Environmental Sciences The University of Adelaide South Australia March 2008 A thesis submitted for the degree of Doctor of Philosophy at The University of Adelaide Who’s Your Daddy? Over the last year, there has been some action happening quietly behind the doors of the Animal Health and Research Centre, and I’m not referring to the treatment of sick animals. I’m talking about sex, and lots of it! This is Meanwhile, mum is left with eight babies to the six-hour continuous lovemaking that has raise without a single child support you hanging from the roof kind of sex. The payment. Luckily the young are born new partner every day kind of sex. The make smaller than a tic-tac, which makes giving love til you drop kind of sex. birth easier. Of the fourteen or so young born, only eight manage to find a teat – for What! I hear you exclaim. That’s outrageous! the others it is just bad luck. Mum carts the kids around continuously for about seven Well before you get too outraged maybe I weeks, then decides they are big enough to should clarify a couple of things. The stay in the nest while she goes ‘out on the individuals involved in this rampant love- tree’. Another seven weeks later and the making are an endangered carnivorous kids are finally ready to leave home, having marsupial known as the red-tailed phascogale.