DOCSLIB.ORG

Review on Point Groups and Symmetry

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Review on Point Groups and Symmetry Review Notes on Point Groups and Symmetry from undergraduate Inorganic Chemistry I course I. Introduction The major difference between organic and inorganic molecules is that organic molecules contain carbon and hydrogen atoms. Inorganic molecules are all compounds that do not contain carbon and hydrogen. Some points regarding inorganic molecules: • They often contain transition metals • Valence electrons in d-orbitals in transition metals are involved in bonding • s, p, d orbitals can be used in bonding (hybridization) • More bonds and geometries are possible around the central atom compared to bonds around a carbon atom Greater geometric complexity in inorganic molecules (about the central atom) related GEOMETRY SYMMETRY Symmetry plays a role in the physical properties of molecules, such as • Bonding- which orbitals interact to form bonds • Absorption spectra - Energy of transitions (position) - Transitions allowed or forbidden (intensity) • Magnetic properties- number of unpaired electrons • Packing of molecules in crystal lattice determines solid state structure and properties II. Symmetry of Objects and Molecules Compare a square to a rectangle. Which is more symmetrical? Why? A 90° rotation from the center about an axis 90o perpendicular to the paper leaves cube unchanged, but No change is apparent rotation not the rectangular object. In general, the square has Square more rotations & reflections that leave it unchanged, there are not as many for the rectangle. This makes 90o the square more symmetrical than then rectangle. Change is apparent rotation We need to relate these symmetry attributes to Rectangle molecules. 1 In general, we define Symmetry: invariance to transformation Transformation: movement of molecule (rotation, reflection, etc.) For example, compare the rotation of an equilateral triangle by 120o with that of a trigonal 120o planar molecule, BF3. When the triangle is No overall rotated, no overall change is apparent. Although rotation change the F’s were interchanged in BF3, we cannot tell because all F’s are equivalent, therefore, if we had not numbered the F atoms, we would say that the 2 o 1 molecule was left unchanged. F 120 F No overall Therefore, for BF , a 120° rotation to the 3 ⊥ change B rotation B plane of the molecule leaves the molecule F F 1 3 F F unchanged. We say that this transformation is a 3 2 symmetry operation of the BF3 molecule. Symmetry operation: a movement of a molecule that leaves the object or molecule unchanged Symmetry element: feature of the molecule that permits a transformation (operation) to be executed which leaves the object or molecule unchanged. Each symmetry operation has a symmetry element associated with it. The ones will be concerned with here are listed below. Operation Element Rotation Axis of rotation Reflection Mirror plane Inversion Center of inversion Improper rotation Axis of improper rotation The symmetry of a given molecule depends which type and how many operations leave it unchanged. Before we go over the symmetry of molecules we will discuss all the operations and their mathematical forms (handout on symmetry operations, matrices). In general, an operation can be thought of as a black box that moves or does something to an object ORIGINAL TRANSFORMED OBJECT OBJECT IN OUT Mathematical Function 2 A. Symmetry Elements and Operations 1. Mirror Plane, Reflection operation (σ) How many mirror planes are there in H2O? Total: 2 σ O • 1 σ bisecting the H-O-H bond (⊥ to paper) H H • 1 σ in the plane of the molecule (contains plane of paper) How about NH3? Total: 3 σ N H H H • 1 σ contains each N-H bond and bisects H-N-H BCl3 (planar molecule)? Total: 4 σ Cl B • 3 σ ⊥ to plane of the molecule along each B-Cl bond Cl Cl • 1 σ in the plane of the molecule (contains all atoms) 2– Planar [PtCl4] ? Total 5 σ; similar to BCl3 We can describe reflections are mathematically, since they are mathematical operations. For example, using Cartesian coordinates, one can ask where does a point (a,b,c) end up after reflection through xz- plane? z z (2,–1,3) (2,1,3) !xz y y or !y x x such that !xz (2,-1,3) (2,1,3) or !y or, in general, !xz (a,b,c) (a,-b,c) or !y 3 Similarly, (a,b,c) !yz (-a,b,c) or !x ! (a,b,c) xy (a,b,-c) or !z Each operation can be written in the form of a matrix. A 3x3 matrix is required for the transformation of an x,y,z point (a,b,c). For example, using the example above for a reflection through the xz plane, σxz, from point P at (a,b,c) to point P´ at (a,-b,c), we can write: P´ = σ xz (P), which means that the reflection operation on point P, σxz (P), results in P´. Since P = (a, b, c) and P´ = (a´, b´, c´) = (a, -b, c), we can write (a´,b´,c´) = σ xz (a,b,c) = (a,-b,c) Using matrices we can then write: a´ 1 0 0 a a b´ = 0 -1 0 b = -b c´ 0 0 1 c c P´ !xz P P´ Similarly, we can write the transformation matrices for σyz and σxy as follows. -1 0 0 1 0 0 !x = !yz = 0 1 0 !z = !xy = 0 1 0 0 0 1 0 0 -1 2. Inversion, center of inversion (i) Inversion operation: takes a point on a line through the origin to an equal distance on the other side For a point at x,y,z coordinates (2,-3,-4) inversion would move the point to (-2,3,4), such that i (2,-3,-4) = (-2,3,4) Therefore, in general, inversion of a point (a,b,c) results in a point at (-a,-b,-c) or i (a,b,c) = (-a,-b,-c) 4 The transformation matrix for inversion is given by -1 0 0 i = 0 -1 0 0 0 -1 If inversion operation is a symmetry operation of the molecule then we can say that: • the molecule possesses a center of symmetry • the molecule in centrosymmetric Do the following molecules have centers of inversion? F Cl 2– Br H Cl Pt Cl Cl M Cl C B Cl Cl H H H F F Cl Br Yes Yes No No 3. Rotation, Axis of Rotation (Cn) Cn = rotation about an axis of n-fold symmetry Cn (axis of rotation) ! An object has axial symmetry if it is invariant to rotation by θ, where n (n = 2π/θ) is an integer. n is the order of rotation θ is the angle of rotation Convention: clockwise rotation looking down axis m Cn means doing the Cn operation m times. n Cn takes the molecule back to starting position 5 Rotations in NH3 (top view): 2 1 3 2 o H H H H ! = 120 Starting C3 C3 C3 n = 3 Point N N N N C 3 H H H H H H H H 1 3 3 2 2 1 1 3 2 C3 3 C3 The general transformation matrix for a Cn rotation about the z-axis is given by cos(2!/ n) sin(2!/ n) 0 z Cn = –sin(2!/ n) cos(2!/ n) 0 0 0 1 So for C2 and C4 rotations about the z-axis cos(!) sin(!) 0 -1 0 0 C2 = –sin(!) cos(!) 0 = 0 -1 0 0 0 1 0 0 1 cos(!/ 2) sin(!/ 2) 0 0 1 0 C4 = –sin(!/ 2) cos(!/ 2) 0 = -1 0 0 0 0 1 0 0 1 The general matrices for Cn rotations about the x and y axes are given by: 1 0 0 cos(2!/ n) 0 sin(2!/ n) x y Cn = 0 cos(2!/ n) sin(2!/ n) Cn = 0 1 0 0 –sin(2!/ n) cos(2!/ n) –sin(2!/ n) 0 cos(2!/ n) All linear molecules have a C∞ axis along the axis of the molecule. They can be rotated by an infinitesimal angle and remain unchanged. 6 2– Example: List the rotational axes and operations present in square planar [PtCl4] . C2 C2´ Axes Operations Cl 2 3 C4 ! plane of molecule C4, C4 = C2, C4 C2 Cl Pt Cl 2 C2 contain Pt-Cl bonds 2 C2 Cl 2 C ´ bisect Cl-Pt-Cl C2´ 2 2 C2´ 4. Identity Operation: E Identity operation leaves a molecule unchanged. The operation E performed on a Cartesian point (a,b,c) results in (a,b,c). The matix for E is given by: 1 0 0 E = 0 1 0 0 0 1 Various operations performed successively result in placing the molecule in the original position, such as one reflection followed by another, inversion followed by inversion, and a Cn rotation performed n times, such that σ • σ = E i • i = E n Cn = E 5. Improper Rotation: Sn (element= axis of improper rotation) The improper rotation, Sn, is defined as a rotation (Cn) followed by reflection (σ) through plane perpendicular to the Cn axis. Cn P → P´ by C , P´ P n P´ → P´´ by σ ! Overall, Sn(P) = P´´ P´´ Sn = Cn × σ = σ × Cn ⇒ the operations commute 7 We can multiply the corresponding matrices for rotation (along z-axis) and reflection to arrive at the transformation matrix for the Sn operation. 1 0 0 cos(2!/ n) sin(2!/ n) 0 Sn = "xy x Cn = 0 1 0 –sin(2!/ n) cos(2!/ n) 0 = 0 0 -1 0 0 1 cos(2!/ n) sin(2!/ n) 0 = –sin(2!/ n) cos(2!/ n) 0 0 0 -1 Doing the Sn operation m times: m = Cn if m = even m m m Sn = Cn × σ = m = Cn × σ if m = odd = E if m = even n n Sn = Cn × σ = = σ if m = odd Example: S4 rotation and its repetitions on CH4 1 H S4 4 H C H H 2 3 Looking down the S4 axis (rotating the CH4 molecule so that S4 arrow points at you): 1 3 3 H H H C4 ! 3 H C H 4 2 H C H 1 2 H C H 1 H H H 2 4 4 S (single operation) 4 8 Notice that there is a C2 axis coincident with the S4 axis that arises from doing the S4 operation two times.
Load more

Recommended publications
  • Symmetry and Tensors Rotations and Tensors
    Symmetry and tensors Rotations and tensors A rotation of a 3-vector is accomplished by an orthogonal transformation. Represented as a matrix, A, we replace each vector, v, by a rotated vector, v0, given by multiplying by A, 0 v = Av In index notation, 0 X vm = Amnvn n Since a rotation must preserve lengths of vectors, we require 02 X 0 0 X 2 v = vmvm = vmvm = v m m Therefore, X X 0 0 vmvm = vmvm m m ! ! X X X = Amnvn Amkvk m n k ! X X = AmnAmk vnvk k;n m Since xn is arbitrary, this is true if and only if X AmnAmk = δnk m t which we can rewrite using the transpose, Amn = Anm, as X t AnmAmk = δnk m In matrix notation, this is t A A = I where I is the identity matrix. This is equivalent to At = A−1. Multi-index objects such as matrices, Mmn, or the Levi-Civita tensor, "ijk, have definite transformation properties under rotations. We call an object a (rotational) tensor if each index transforms in the same way as a vector. An object with no indices, that is, a function, does not transform at all and is called a scalar. 0 A matrix Mmn is a (second rank) tensor if and only if, when we rotate vectors v to v , its new components are given by 0 X Mmn = AmjAnkMjk jk This is what we expect if we imagine Mmn to be built out of vectors as Mmn = umvn, for example. In the same way, we see that the Levi-Civita tensor transforms as 0 X "ijk = AilAjmAkn"lmn lmn 1 Recall that "ijk, because it is totally antisymmetric, is completely determined by only one of its components, say, "123.
    [Show full text]
  • Properties of the Single and Double D4d Groups and Their Isomorphisms with D8 and C8v Groups A
    Properties of the single and double D4d groups and their isomorphisms with D8 and C8v groups A. Le Paillier-Malécot, L. Couture To cite this version: A. Le Paillier-Malécot, L. Couture. Properties of the single and double D4d groups and their isomorphisms with D8 and C8v groups. Journal de Physique, 1981, 42 (11), pp.1545-1552. 10.1051/jphys:0198100420110154500. jpa-00209347 HAL Id: jpa-00209347 https://hal.archives-ouvertes.fr/jpa-00209347 Submitted on 1 Jan 1981 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. J. Physique 42 (1981) 1545-1552 NOVEMBRE 1981, 1545 Classification Physics Abstracts 75.10D Properties of the single and double D4d groups and their isomorphisms with D8 and C8v groups A. Le Paillier-Malécot Laboratoire de Magnétisme et d’Optique des Solides, 1, place A.-Briand, 92190 Meudon Bellevue, France and Université de Paris-Sud XI, Centre d’Orsay, 91405 Orsay Cedex, France and L. Couture Laboratoire Aimé-Cotton (*), C.N.R.S., Campus d’Orsay, 91405 Orsay Cedex, France and Laboratoire d’Optique et de Spectroscopie Cristalline, Université Pierre-et-Marie-Curie, Paris VI, 75230 Paris Cedex 05, France (Reçu le 15 mai 1981, accepté le 9 juillet 1981) Résumé.
    [Show full text]
  • Molecular Symmetry
    Molecular Symmetry Symmetry helps us understand molecular structure, some chemical properties, and characteristics of physical properties (spectroscopy) – used with group theory to predict vibrational spectra for the identification of molecular shape, and as a tool for understanding electronic structure and bonding. Symmetrical : implies the species possesses a number of indistinguishable configurations. 1 Group Theory : mathematical treatment of symmetry. symmetry operation – an operation performed on an object which leaves it in a configuration that is indistinguishable from, and superimposable on, the original configuration. symmetry elements – the points, lines, or planes to which a symmetry operation is carried out. Element Operation Symbol Identity Identity E Symmetry plane Reflection in the plane σ Inversion center Inversion of a point x,y,z to -x,-y,-z i Proper axis Rotation by (360/n)° Cn 1. Rotation by (360/n)° Improper axis S 2. Reflection in plane perpendicular to rotation axis n Proper axes of rotation (C n) Rotation with respect to a line (axis of rotation). •Cn is a rotation of (360/n)°. •C2 = 180° rotation, C 3 = 120° rotation, C 4 = 90° rotation, C 5 = 72° rotation, C 6 = 60° rotation… •Each rotation brings you to an indistinguishable state from the original. However, rotation by 90° about the same axis does not give back the identical molecule. XeF 4 is square planar. Therefore H 2O does NOT possess It has four different C 2 axes. a C 4 symmetry axis. A C 4 axis out of the page is called the principle axis because it has the largest n . By convention, the principle axis is in the z-direction 2 3 Reflection through a planes of symmetry (mirror plane) If reflection of all parts of a molecule through a plane produced an indistinguishable configuration, the symmetry element is called a mirror plane or plane of symmetry .
    [Show full text]
  • The Cubic Groups
    The Cubic Groups Baccalaureate Thesis in Electrical Engineering Author: Supervisor: Sana Zunic Dr. Wolfgang Herfort 0627758 Vienna University of Technology May 13, 2010 Contents 1 Concepts from Algebra 4 1.1 Groups . 4 1.2 Subgroups . 4 1.3 Actions . 5 2 Concepts from Crystallography 6 2.1 Space Groups and their Classification . 6 2.2 Motions in R3 ............................. 8 2.3 Cubic Lattices . 9 2.4 Space Groups with a Cubic Lattice . 10 3 The Octahedral Symmetry Groups 11 3.1 The Elements of O and Oh ..................... 11 3.2 A Presentation of Oh ......................... 14 3.3 The Subgroups of Oh ......................... 14 2 Abstract After introducing basics from (mathematical) crystallography we turn to the description of the octahedral symmetry groups { the symmetry group(s) of a cube. Preface The intention of this account is to provide a description of the octahedral sym- metry groups { symmetry group(s) of the cube. We first give the basic idea (without proofs) of mathematical crystallography, namely that the 219 space groups correspond to the 7 crystal systems. After this we come to describing cubic lattices { such ones that are built from \cubic cells". Finally, among the cubic lattices, we discuss briefly the ones on which O and Oh act. After this we provide lists of the elements and the subgroups of Oh. A presentation of Oh in terms of generators and relations { using the Dynkin diagram B3 is also given. It is our hope that this account is accessible to both { the mathematician and the engineer. The picture on the title page reflects Ha¨uy'sidea of crystal structure [4].
    [Show full text]
  • Chapter 1 – Symmetry of Molecules – P. 1
    Chapter 1 – Symmetry of Molecules – p. 1 - 1. Symmetry of Molecules 1.1 Symmetry Elements · Symmetry operation: Operation that transforms a molecule to an equivalent position and orientation, i.e. after the operation every point of the molecule is coincident with an equivalent point. · Symmetry element: Geometrical entity (line, plane or point) which respect to which one or more symmetry operations can be carried out. In molecules there are only four types of symmetry elements or operations: · Mirror planes: reflection with respect to plane; notation: s · Center of inversion: inversion of all atom positions with respect to inversion center, notation i · Proper axis: Rotation by 2p/n with respect to the axis, notation Cn · Improper axis: Rotation by 2p/n with respect to the axis, followed by reflection with respect to plane, perpendicular to axis, notation Sn Formally, this classification can be further simplified by expressing the inversion i as an improper rotation S2 and the reflection s as an improper rotation S1. Thus, the only symmetry elements in molecules are Cn and Sn. Important: Successive execution of two symmetry operation corresponds to another symmetry operation of the molecule. In order to make this statement a general rule, we require one more symmetry operation, the identity E. (1.1: Symmetry elements in CH4, successive execution of symmetry operations) 1.2. Systematic classification by symmetry groups According to their inherent symmetry elements, molecules can be classified systematically in so called symmetry groups. We use the so-called Schönfliess notation to name the groups, Chapter 1 – Symmetry of Molecules – p. 2 - which is the usual notation for molecules.
    [Show full text]
  • COXETER GROUPS (Unfinished and Comments Are Welcome)
    COXETER GROUPS (Unfinished and comments are welcome) Gert Heckman Radboud University Nijmegen [email protected] October 10, 2018 1 2 Contents Preface 4 1 Regular Polytopes 7 1.1 ConvexSets............................ 7 1.2 Examples of Regular Polytopes . 12 1.3 Classification of Regular Polytopes . 16 2 Finite Reflection Groups 21 2.1 NormalizedRootSystems . 21 2.2 The Dihedral Normalized Root System . 24 2.3 TheBasisofSimpleRoots. 25 2.4 The Classification of Elliptic Coxeter Diagrams . 27 2.5 TheCoxeterElement. 35 2.6 A Dihedral Subgroup of W ................... 39 2.7 IntegralRootSystems . 42 2.8 The Poincar´eDodecahedral Space . 46 3 Invariant Theory for Reflection Groups 53 3.1 Polynomial Invariant Theory . 53 3.2 TheChevalleyTheorem . 56 3.3 Exponential Invariant Theory . 60 4 Coxeter Groups 65 4.1 Generators and Relations . 65 4.2 TheTitsTheorem ........................ 69 4.3 The Dual Geometric Representation . 74 4.4 The Classification of Some Coxeter Diagrams . 77 4.5 AffineReflectionGroups. 86 4.6 Crystallography. .. .. .. .. .. .. .. 92 5 Hyperbolic Reflection Groups 97 5.1 HyperbolicSpace......................... 97 5.2 Hyperbolic Coxeter Groups . 100 5.3 Examples of Hyperbolic Coxeter Diagrams . 108 5.4 Hyperbolic reflection groups . 114 5.5 Lorentzian Lattices . 116 3 6 The Leech Lattice 125 6.1 ModularForms ..........................125 6.2 ATheoremofVenkov . 129 6.3 The Classification of Niemeier Lattices . 132 6.4 The Existence of the Leech Lattice . 133 6.5 ATheoremofConway . 135 6.6 TheCoveringRadiusofΛ . 137 6.7 Uniqueness of the Leech Lattice . 140 4 Preface Finite reflection groups are a central subject in mathematics with a long and rich history. The group of symmetries of a regular m-gon in the plane, that is the convex hull in the complex plane of the mth roots of unity, is the dihedral group of order 2m, which is the simplest example of a reflection Dm group.
    [Show full text]
  • Symmetry of Graphs. Circles
    Symmetry of graphs. Circles Symmetry of graphs. Circles 1 / 10 Today we will be interested in reflection across the x-axis, reflection across the y-axis and reflection across the origin. Reflection across y reflection across x reflection across (0; 0) Sends (x,y) to (-x,y) Sends (x,y) to (x,-y) Sends (x,y) to (-x,-y) Examples with Symmetry What is Symmetry? Take some geometrical object. It is called symmetric if some geometric move preserves it Symmetry of graphs. Circles 2 / 10 Reflection across y reflection across x reflection across (0; 0) Sends (x,y) to (-x,y) Sends (x,y) to (x,-y) Sends (x,y) to (-x,-y) Examples with Symmetry What is Symmetry? Take some geometrical object. It is called symmetric if some geometric move preserves it Today we will be interested in reflection across the x-axis, reflection across the y-axis and reflection across the origin. Symmetry of graphs. Circles 2 / 10 Sends (x,y) to (-x,y) Sends (x,y) to (x,-y) Sends (x,y) to (-x,-y) Examples with Symmetry What is Symmetry? Take some geometrical object. It is called symmetric if some geometric move preserves it Today we will be interested in reflection across the x-axis, reflection across the y-axis and reflection across the origin. Reflection across y reflection across x reflection across (0; 0) Symmetry of graphs. Circles 2 / 10 Sends (x,y) to (-x,y) Sends (x,y) to (x,-y) Sends (x,y) to (-x,-y) Examples with Symmetry What is Symmetry? Take some geometrical object.
    [Show full text]
  • Symmetry in Chemistry
    SYMMETRY IN CHEMISTRY Professor MANOJ K. MISHRA CHEMISTRY DEPARTMENT IIT BOMBAY ACKNOWLEGDEMENT: Professor David A. Micha Professor F. A. Cotton 1 An introduction to symmetry analysis WHY SYMMETRY ? Hψ = Eψ For H – atom: Each member of the CSCO labels, For molecules: Symmetry operation R CSCO H is INVARIANT under R ( by definition too) 2 An introduction to symmetry analysis Hψ = Eψ gives NH3 normal modes = NH3 rotation or translation MUST be A1, A2 or E ! NO ESCAPING SYMMETRY! 3 Molecular Symmetry An introduction to symmetry analysis (Ref.: Inorganic chemistry by Shirver, Atkins & Longford, ELBS) One aspect of the shape of a molecule is its symmetry (we define technical meaning of this term in a moment) and the systematic treatment and symmetry uses group theory. This is a rich and powerful subject, by will confine our use of it at this stage to classifying molecules and draw some general conclusions about their properties. An introduction to symmetry analysis Our initial aim is to define the symmetry of molecules much more precisely than we have done so far, and to provide a notational scheme that confirms their symmetry. In subsequent chapters we extend the material present here to applications in bonding and spectroscopy, and it will become that symmetry analysis is one of the most pervasive techniques in inorganic chemistry. Symmetry operations and elements A fundamental concept of group theory is the symmetry operation. It is an action, such as a rotation through a certain angle, that leave molecules apparently unchanged. An example is the rotation of H2O molecule by 180 ° (but not any smaller angle) around the bisector of HOH angle.
    [Show full text]
  • Rotation Matrix - Wikipedia, the Free Encyclopedia Page 1 of 22
    Rotation matrix - Wikipedia, the free encyclopedia Page 1 of 22 Rotation matrix From Wikipedia, the free encyclopedia In linear algebra, a rotation matrix is a matrix that is used to perform a rotation in Euclidean space. For example the matrix rotates points in the xy -Cartesian plane counterclockwise through an angle θ about the origin of the Cartesian coordinate system. To perform the rotation, the position of each point must be represented by a column vector v, containing the coordinates of the point. A rotated vector is obtained by using the matrix multiplication Rv (see below for details). In two and three dimensions, rotation matrices are among the simplest algebraic descriptions of rotations, and are used extensively for computations in geometry, physics, and computer graphics. Though most applications involve rotations in two or three dimensions, rotation matrices can be defined for n-dimensional space. Rotation matrices are always square, with real entries. Algebraically, a rotation matrix in n-dimensions is a n × n special orthogonal matrix, i.e. an orthogonal matrix whose determinant is 1: . The set of all rotation matrices forms a group, known as the rotation group or the special orthogonal group. It is a subset of the orthogonal group, which includes reflections and consists of all orthogonal matrices with determinant 1 or -1, and of the special linear group, which includes all volume-preserving transformations and consists of matrices with determinant 1. Contents 1 Rotations in two dimensions 1.1 Non-standard orientation
    [Show full text]
  • Chapter 3: Transformations Groups, Orbits, and Spaces of Orbits
    Preprint typeset in JHEP style - HYPER VERSION Chapter 3: Transformations Groups, Orbits, And Spaces Of Orbits Gregory W. Moore Abstract: This chapter focuses on of group actions on spaces, group orbits, and spaces of orbits. Then we discuss mathematical symmetric objects of various kinds. May 3, 2019 -TOC- Contents 1. Introduction 2 2. Definitions and the stabilizer-orbit theorem 2 2.0.1 The stabilizer-orbit theorem 6 2.1 First examples 7 2.1.1 The Case Of 1 + 1 Dimensions 11 3. Action of a topological group on a topological space 14 3.1 Left and right group actions of G on itself 19 4. Spaces of orbits 20 4.1 Simple examples 21 4.2 Fundamental domains 22 4.3 Algebras and double cosets 28 4.4 Orbifolds 28 4.5 Examples of quotients which are not manifolds 29 4.6 When is the quotient of a manifold by an equivalence relation another man- ifold? 33 5. Isometry groups 34 6. Symmetries of regular objects 36 6.1 Symmetries of polygons in the plane 39 3 6.2 Symmetry groups of some regular solids in R 42 6.3 The symmetry group of a baseball 43 7. The symmetries of the platonic solids 44 7.1 The cube (\hexahedron") and octahedron 45 7.2 Tetrahedron 47 7.3 The icosahedron 48 7.4 No more regular polyhedra 50 7.5 Remarks on the platonic solids 50 7.5.1 Mathematics 51 7.5.2 History of Physics 51 7.5.3 Molecular physics 51 7.5.4 Condensed Matter Physics 52 7.5.5 Mathematical Physics 52 7.5.6 Biology 52 7.5.7 Human culture: Architecture, art, music and sports 53 7.6 Regular polytopes in higher dimensions 53 { 1 { 8.
    [Show full text]
  • Crystallography: Symmetry Groups and Group Representations B
    EPJ Web of Conferences 22, 00006 (2012) DOI: 10.1051/epjconf/20122200006 C Owned by the authors, published by EDP Sciences, 2012 Crystallography: Symmetry groups and group representations B. Grenier1 and R. Ballou2 1SPSMS, UMR-E 9001, CEA-INAC / UJF-Grenoble, MDN, 38054 Grenoble, France 2Institut Néel, CNRS / UJF, 25 rue des Martyrs, BP. 166, 38042 Grenoble Cedex 9, France Abstract. This lecture is aimed at giving a sufficient background on crystallography, as a reminder to ease the reading of the forthcoming chapters. It more precisely recalls the crystallographic restrictions on the space isometries, enumerates the point groups and the crystal lattices consistent with these, examines the structure of the space group, which gathers all the spatial invariances of a crystal, and describes a few dual notions. It next attempts to familiarize us with the representation analysis of physical states and excitations of crystals. 1. INTRODUCTION Crystallography covers a wide spectrum of investigations: i- it aspires to get an insight into crystallization phenomena and develops methods of crystal growths, which generally pertains to the physics of non linear irreversible processes; ii- it geometrically describes the natural shapes and the internal structures of the crystals, which is carried out most conveniently by borrowing mathematical tools from group theory; iii- it investigates the crystallized matter at the atomic scale by means of diffraction techniques using X-rays, electrons or neutrons, which are interpreted in the dual context of the reciprocal space and transposition therein of the crystal symmetries; iv- it analyzes the imperfections of the crystals, often directly visualized in scanning electron, tunneling or force microscopies, which in some instances find a meaning by handling unfamiliar concepts from homotopy theory; v- it aims at providing means for discerning the influences of the crystal structure on the physical properties of the materials, which requires to make use of mathematical methods from representation theory.
    [Show full text]
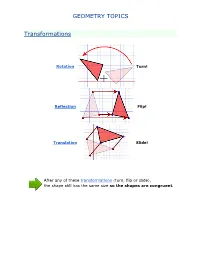
  • Geometry Topics
    GEOMETRY TOPICS Transformations Rotation Turn! Reflection Flip! Translation Slide! After any of these transformations (turn, flip or slide), the shape still has the same size so the shapes are congruent. Rotations Rotation means turning around a center. The distance from the center to any point on the shape stays the same. The rotation has the same size as the original shape. Here a triangle is rotated around the point marked with a "+" Translations In Geometry, "Translation" simply means Moving. The translation has the same size of the original shape. To Translate a shape: Every point of the shape must move: the same distance in the same direction. Reflections A reflection is a flip over a line. In a Reflection every point is the same distance from a central line. The reflection has the same size as the original image. The central line is called the Mirror Line ... Mirror Lines can be in any direction. Reflection Symmetry Reflection Symmetry (sometimes called Line Symmetry or Mirror Symmetry) is easy to see, because one half is the reflection of the other half. Here my dog "Flame" has her face made perfectly symmetrical with a bit of photo magic. The white line down the center is the Line of Symmetry (also called the "Mirror Line") The reflection in this lake also has symmetry, but in this case: -The Line of Symmetry runs left-to-right (horizontally) -It is not perfect symmetry, because of the lake surface. Line of Symmetry The Line of Symmetry (also called the Mirror Line) can be in any direction. But there are four common directions, and they are named for the line they make on the standard XY graph.
    [Show full text]