DOCSLIB.ORG

Correlation of Surface and Interfacial Tension of Light Hydrocarbons in the Critical Region

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Correlation of Surface and Interfacial Tension of Light Hydrocarbons in the Critical Region Correlation of Surface and Interfacial Tension of Light Hydrocarbons in the Critical Region E.W.HOUGH* THE U. OF TEXAS MEMBER AIME AUSTIN. TEX. G. L. STEGEMEIER SHELL DEVELOPMENT CO. JUNIOR MEMBER AIME HOUSTON. TEX. Downloaded from http://onepetro.org/spejournal/article-pdf/1/04/259/2152696/spe-197-pa.pdf by guest on 28 September 2021 ABSTRACT Interfacial tension is defined as the specific Empirical equations for surface tension of propane surface-free energy between two phases of unlike and normal butane as functions of reduced temper­ fractional composition, while surface tension is ature are obtained from experimental data. Another defined as the specific surface-free energy between correlation relating surface tension to enthalpy of two phases of the same fractional composition. The vaporization is given for these two compounds. In usual definitions relating interfacial tension to a addition, new parachor numbers are calculated for liquid-liquid interface and surface tension to a the normal paraffin hydrocarbons. These numbers gas-liquid interface are not clearly defined when are utilized for the calculation of interfacial tension the critical regi~n is included, and there is no sharp of two-component systems as functions of pressure distinction between a gas and a liquid phase. and Jemperature, using a modified form of Weinaug­ Interfacial tension is probably the most important Katz equation. The experimental data for two binary single force that makes one-half to one-third of the systems are approximated by the correlation. From total oil actually in place in a reservoir rock un­ these results it is found that the interfacial tension recoverable by conventional gas-drive or waterflood in the high-pressure region remains extremely low methods. A rough estimate of this figure for the at large pressure decrements below the critical United States is 100 billion bbl. Interfacial tension pressure. Thus, it appears that condensate systems presently is used by petroleum engineers in the may have flow characteristics almost like single­ estimation of saturation gradients at the gas-oil phase conditions even though the pressure is within contact and at the oil-water contact. The data in the two-phase region. this paper should prove useful for estimates of Experimental data have shown that interfacial reserves involving gas-oil contacts. Relative per­ tension divided by density difference approaches meability undoubtedly is influenced by interfacial zero as the critical pressure is approached. A tension, for sufficiently small values. These data calculation of wetting-phase saturations indicates should be useful in determining how small the that the saturation gradient at the two-phase contact values are. In addition, these data should eventually becomes increasingly abrupt as the critical pressure add to our fundamental knowledge of surfaces. At is approached. the critical point, all surface excesses approach zero and the thickness becomes very large. DISCUSSION SINGLE-COMPONENT SYSTEMS Prediction of the surface and interfacial tension l of the light hydrocarbons and of two-component It has been observed that the following relation­ hydrocarbon mixtures at various temperatures and ships are good approximations to the physical pressures may be made i£ other physical properties properties of propane and n-butane. are known. Extensive experimental work on single­ For propane, I'lp = 0.80 (l_TITc )O.326, Y = 49.5 component and binary systems 1 is the basis for (I-TITc )l.20, y/i"J.p = 61.9 (I-TITc )O.874, and the correlations outlined in this paper. y = 112.5 i"J.,,-3.68. For n-butane, i"J.p = 0.86 (1-TIT c)O.333, Y = 52.5 Original manuscript received in Society of Petroleum Engi­ neers office June 12, 1961. Revised manuscript received Sept. (1 ~TITc)1.22, y/i"J.p = 61.0 (I-TITc )O.887 and 29, 1961. Acknowledgment is made with thanks to API Grant­ y = 91.2 1'lp3.66. in-Aid 45, to the Shell Oil Co. for a fellowship which supported 0 .... of us, and to The U. of Texas which purchased much of Guggenheim's2 values for these constants not the equipment used on a special grant. specifically for hydrocarbons, are i"J.p = C,' (1- -Now head of Petroleum Enaineering Dept. at Mississippi State U. TITc)l/3, Y = C"(I-TITc)11/9, y/I'lp = C"'(l­ TITc)8/9, and y = Ci"J.pll/3. lReferences given at end of paper. SPE 197 DECEMBER, 1961 259 Reprinted from the December. 1961. Issue of SOCIETY OF PETROLEUM ENGINEERS JOURNAL The symbols and units are and ethane appear to diverge slightly from this !':!p = difference in density of the liquid pattern. Some of this divergence is probably caused and vapor phases, gm/cc, by the measurement of surface tension against air rather than its own vapor, and by the neglect of the y = surface tension, dynes/em, vapor density. T = absolute temperature, oR or oK, A correlation suggested by Magaril7 relates the Tc critical temperature (absolute), oR = enthalpy of vaporization at constant pressure to the or oK, and surface tension. Tables 2 and 3 and Figs. 2 and 3 C: C'~ C'" = constants. express this relation for propane and for n-butane. The exponents for propane and n-butane are taken The straight-line relationship on log-log paper from log-log plots. The last equation may be recog­ appears to deviate slightly as the critical point is nized as the surface tension-density difference re­ approached. lationship leading to Sugden's parachor,3 with the exponent "3/11" rather than "1/4". That is, TWO-COMPONENT SYSTEMS P = MC3/11 = M y3/11 Prediction of interfacial tension in two-component /1p systems is much more difficult than in the single­ component systems because of the added composition Downloaded from http://onepetro.org/spejournal/article-pdf/1/04/259/2152696/spe-197-pa.pdf by guest on 28 September 2021 where P = parachor, and variable. The correlation suggested by Weinaug and M = molecular weight. Katz 8 has been used with the new exponent and From this modified equation, new values of slightly modified for use with molal volumes rather parachor were calculated for some of the normal than specific gravity. The relation is paraffin hydrocarbons. Surface-tension and density­ difference data for methane, ethane, n-decane and y ={ 6/43 fl (xliV x - yl/Vy ) n-e icosane were taken from Rossini,4 for n-pentane from Sage and LaceyS and from Katz,6 and for pro­ + P2 (x2 /Vx - Y2 IVy ~ pane and n-butane from Sage and Lacey and from r experimental work'! The values are shown in Table where y interfacial tension, dynes/em, 1. Because the parachor is (ideally) independent = of temperature, the values of surface tension and PI "" parachor of the first component, density difference were selected at the temperature P 2 = parachor of the second component, at which the best data were obtainable or at the 1000 temperature at which the vapor density is negligible if this latter data were not available. Fig. 1 shows 900 II a regular increase in the parachor with an increase I in molecular size from 3 to 20 carbon atoms. Methane II 800 TABLE 1 - PARACI:IOR OF NORMAL PARAFFIN HYDROCARBONS V Density Surf. or 700 Carbon Temp. Diff. Intf. Tens. Compound Atoms ~ (gm/cc) (dynes/cm) Parachor V 600 II Methane - 256 0.4218 R 13.7R 77.9 0:: R R o V Ethane 2 - 238 0.620 26.34 118.0 :r: 8 V Propane 3 100 0.443 5.47 158. 1 ~ 500 5.45 K 158 0:: ~ D C~I E n-Butane 4 120 0.5328 9.27 200.5 V~ 9.20 200 400 n-Pentane 5 100 0.603 8 14.0K 246 II ; R R i n-Decane 10 68 0.730 23.92 463 300 I n-Eicosane 20 100 0.7754 R 27.2 R 899 I P~N TIN R=Rossini (Ref. 4); S=Sage and Lacey (Ref. 5); and K=Katz II n (Ref. 6). 200 I .~ R )1 !A.I~E ! TABLE 2 - ENTHALPY OF VAPORIZATION AT H,,~ E CONSTANT PRESSURE - PROPANE 100 VaT T~t N Enthalpy of ~'E Temperature Vaporization* Surface Tension** (0 F) (calorieslgm-mol) (dynes/cm) o 3 5 7 9 (( 13 15 17 19 100 3271 5.48 2 4 6 8 10 12 14 16 18 20 3.66 130 2878 NUMBER OF CARBON ATOMS 2366 1.97 160 IN MOLECULE 190 1660 0.58 *Sage and Lacey (Ref. 5). FIG. I - PARACHOR, NORMAL PARAFFIN **Current paper. HYDROCARBONS. 260 SOCIETY OF PETROLEUM ENGINEERS JOURNAL TABLE 3 - ENTHALPY OF VAPORIZATION AT critical loci is also the line of zero interfacial CONSTANT PRESSURE - NORMAL BUTANE tension; hence, the subsequent iso-interfacial Enthalpy of tension lines must roughly parallel this boundary. Temperature Vaparizatian* Surface Tensian** These data and assumptions allow extrapolation (0 F) (calaries/gm.moll (dynes/em) and interpolation to all points within the two-phase 100 4816 10.49 region. It is evident from these plots that the inter­ 130 4566 8.67 facial tension of a binary mixture in the temperature 160 4266 6.88 range in which the critical pressure is high increases 190 3912 5.14 220 3498 3.48 much more slowly with a decrease in pressure than 250 2980 2.02 either of the pure components. In the case of the 280 2307 0.80 methane-normal pentane system, a pressure drop *Sage and Lacey (Ref. 5). of 450 psi from the critical pressure is required **Current paper. at lOOoF before the interfacial tension reaches 1 dyne/cm. The same increase for the pure components = mol fraction in the liquid phase, Xv X2 occurs with a pressure drop of about 120 psi.
Load more

Recommended publications
  • Safety Data Sheet Acc
    Page 1/8 Safety Data Sheet acc. to OSHA HCS Printing date 03/18/2019 Reviewed on 03/18/2019 1 Identification · Product identifier · Product Name: EVEN ALK (C16-C36) · Part Number: ENC-EVEN-1K · Application of the substance / the mixture Certified Reference Material · Details of the supplier of the safety data sheet · Manufacturer/Supplier: SPEX CertiPrep, LLC. 203 Norcross Ave, Metuchen, NJ 08840 USA · Information department: product safety department · Emergency telephone number: Emergency Phone Number (24 hours) CHEMTREC (800-424-9300) Outside US: 703-527-3887 2 Hazard(s) identification · Classification of the substance or mixture GHS02 Flame Flam. Liq. 2 H225 Highly flammable liquid and vapor. GHS08 Health hazard Carc. 2 H351 Suspected of causing cancer. GHS07 Acute Tox. 4 H302 Harmful if swallowed. · Label elements · GHS label elements The product is classified and labeled according to the Globally Harmonized System (GHS). · Hazard pictograms GHS02 GHS07 GHS08 · Signal word Danger · Hazard-determining components of labeling: dichloromethane · Hazard statements H225 Highly flammable liquid and vapor. H302 Harmful if swallowed. H351 Suspected of causing cancer. · Precautionary statements Keep away from heat/sparks/open flames/hot surfaces. - No smoking. Use explosion-proof electrical/ventilating/lighting/equipment. Wear protective gloves/protective clothing/eye protection/face protection. If on skin (or hair): Take off immediately all contaminated clothing. Rinse skin with water/shower. Store locked up. Dispose of contents/container in accordance with local/regional/national/international regulations. · Classification system: · NFPA ratings (scale 0 - 4) Health = 1 3 Fire = 3 1 0 Reactivity = 0 (Contd. on page 2) US 48.1.17.1 Page 2/8 Safety Data Sheet acc.
    [Show full text]
  • Managing Health Risks of Solvent
    BEST PRACTICE GUIDELINES Managing the Health Risks of Solvent Exposure Managing the Health Risks of Solvent Exposure September 2015 CONTENTS 1 Introduction 5 1.1 SCOPE AND OBJECTIVES 5 2 The regulatory landscape 6 2.1 CAD 6 2.2 REACH 6 2.3 CLP 8 3 Health effects and properties of solvents 9 3.1 EFFECTS OF SOLVENTS VIA SKIN AND EYE CONTACT 9 3.2 EFFECTS VIA INHALATION 10 3.3 CLASSIFICATION AND LABELLING OF SOLVENTS 10 3.4 HAZARD AND RISK 11 4 Exposure scenarios (es) - Basic principles 12 4.1 DEVELOPING AN ES 13 4.2 SOLVENTS MANUFACTURERS MEET THE CHALLENGE OF DEVELOPING ES 13 5 The solvents industry’s approach to REACH 14 5.1 NAMING CONVENTION FOR HYDROCARBON SOLVENTS 14 5.2 DEVELOPMENT OF GENERIC EXPOSURE SCENARIOS (GES) 14 5.2.1 THE USE DESCRIPTOR SYSTEM (UDS) (REF 15) 15 5.2.2 THE ESIG GES LIBRARY 15 6 Exposure limit values for solvents 17 6.1 OELs AND DNELs 17 6.2 INDUSTRY-BASED OELs FOR HYDROCARBON SOLVENTS 18 ManagingFlammability: the Health Risks A safety of Solvent guide Exposurefor users 7 Responsibilities of solvent users 19 8 Role of solvent vapour monitoring 23 9 Key messages 24 10 List of acronyms 25 11 References 28 APPENDIX 1 Overview of control approaches for solvents required by CAD 29 APPENDIX 2 CLP Classification phrases for solvents 30 APPENDIX 3 Hydrocarbon solvents registered under REACH - key data 31 APPENDIX 4 Oxygenated solvents registered under REACH - key data 43 APPENDIX 5 Example ES for a hydrocarbon solvent containing N-Hexane (>5-80%) 50 APPENDIX 6 List of common solvent uses matched to ESIG generic exposure scenario (GES) title with examples of relevant solvent types 53 APPENDIX 7 Mixtures 62 3 Managing the Health Risks of Solvent Exposure DISCLAIMER The information contained in this paper is intended for guidance only and whilst the information is provided in utmost good faith and has been based on the best information currently available, it is to be relied upon at the user’s own risk.
    [Show full text]
  • Adsorption of Light Alkanes on the Surface of Substrates with Varying Symmetry and Composition
    University of Tennessee, Knoxville TRACE: Tennessee Research and Creative Exchange Doctoral Dissertations Graduate School 5-2018 Adsorption of Light Alkanes on the Surface of Substrates with Varying Symmetry and Composition Nicholas Allan Strange University of Tennessee Follow this and additional works at: https://trace.tennessee.edu/utk_graddiss Recommended Citation Strange, Nicholas Allan, "Adsorption of Light Alkanes on the Surface of Substrates with Varying Symmetry and Composition. " PhD diss., University of Tennessee, 2018. https://trace.tennessee.edu/utk_graddiss/4967 This Dissertation is brought to you for free and open access by the Graduate School at TRACE: Tennessee Research and Creative Exchange. It has been accepted for inclusion in Doctoral Dissertations by an authorized administrator of TRACE: Tennessee Research and Creative Exchange. For more information, please contact [email protected]. To the Graduate Council: I am submitting herewith a dissertation written by Nicholas Allan Strange entitled "Adsorption of Light Alkanes on the Surface of Substrates with Varying Symmetry and Composition." I have examined the final electronic copy of this dissertation for form and content and recommend that it be accepted in partial fulfillment of the equirr ements for the degree of Doctor of Philosophy, with a major in Chemistry. John Z. Larese, Major Professor We have read this dissertation and recommend its acceptance: Takeshi Egami, Jeffrey D. Kovac, Brian K. Long Accepted for the Council: Dixie L. Thompson Vice Provost and Dean of the Graduate School (Original signatures are on file with official studentecor r ds.) Adsorption of Light Alkanes on the Surface of Substrates with Varying Symmetry and Composition A Dissertation Presented for the Doctor of Philosophy Degree The University of Tennessee, Knoxville Nicholas Allan Strange May 2018 Copyright © 2018 by Nicholas A.
    [Show full text]
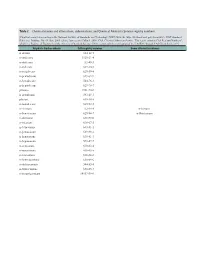
  • Table 2. Chemical Names and Alternatives, Abbreviations, and Chemical Abstracts Service Registry Numbers
    Table 2. Chemical names and alternatives, abbreviations, and Chemical Abstracts Service registry numbers. [Final list compiled according to the National Institute of Standards and Technology (NIST) Web site (http://webbook.nist.gov/chemistry/); NIST Standard Reference Database No. 69, June 2005 release, last accessed May 9, 2008. CAS, Chemical Abstracts Service. This report contains CAS Registry Numbers®, which is a Registered Trademark of the American Chemical Society. CAS recommends the verification of the CASRNs through CAS Client ServicesSM] Aliphatic hydrocarbons CAS registry number Some alternative names n-decane 124-18-5 n-undecane 1120-21-4 n-dodecane 112-40-3 n-tridecane 629-50-5 n-tetradecane 629-59-4 n-pentadecane 629-62-9 n-hexadecane 544-76-3 n-heptadecane 629-78-7 pristane 1921-70-6 n-octadecane 593-45-3 phytane 638-36-8 n-nonadecane 629-92-5 n-eicosane 112-95-8 n-Icosane n-heneicosane 629-94-7 n-Henicosane n-docosane 629-97-0 n-tricosane 638-67-5 n-tetracosane 643-31-1 n-pentacosane 629-99-2 n-hexacosane 630-01-3 n-heptacosane 593-49-7 n-octacosane 630-02-4 n-nonacosane 630-03-5 n-triacontane 638-68-6 n-hentriacontane 630-04-6 n-dotriacontane 544-85-4 n-tritriacontane 630-05-7 n-tetratriacontane 14167-59-0 Table 2. Chemical names and alternatives, abbreviations, and Chemical Abstracts Service registry numbers.—Continued [Final list compiled according to the National Institute of Standards and Technology (NIST) Web site (http://webbook.nist.gov/chemistry/); NIST Standard Reference Database No.
    [Show full text]
  • Section 2. Hazards Identification OSHA/HCS Status : This Material Is Considered Hazardous by the OSHA Hazard Communication Standard (29 CFR 1910.1200)
    SAFETY DATA SHEET Flammable Liquid Mixture: Docosane / Dodecane / Eicosane / Hexadecane / Hexane / N-Decane / N-Heptane / N-Nonane / N-Octadecane / N-Octane / N-Tridecane / Tetracosane / Tetradecane / Undecane Section 1. Identification GHS product identifier : Flammable Liquid Mixture: Docosane / Dodecane / Eicosane / Hexadecane / Hexane / N-Decane / N-Heptane / N-Nonane / N-Octadecane / N-Octane / N-Tridecane / Tetracosane / Tetradecane / Undecane Other means of : Not available. identification Product use : Synthetic/Analytical chemistry. SDS # : 018777 Supplier's details : Airgas USA, LLC and its affiliates 259 North Radnor-Chester Road Suite 100 Radnor, PA 19087-5283 1-610-687-5253 24-hour telephone : 1-866-734-3438 Section 2. Hazards identification OSHA/HCS status : This material is considered hazardous by the OSHA Hazard Communication Standard (29 CFR 1910.1200). Classification of the : FLAMMABLE LIQUIDS - Category 1 substance or mixture SKIN CORROSION/IRRITATION - Category 2 SERIOUS EYE DAMAGE/ EYE IRRITATION - Category 2A TOXIC TO REPRODUCTION (Fertility) - Category 2 TOXIC TO REPRODUCTION (Unborn child) - Category 2 SPECIFIC TARGET ORGAN TOXICITY (SINGLE EXPOSURE) (Respiratory tract irritation) - Category 3 SPECIFIC TARGET ORGAN TOXICITY (SINGLE EXPOSURE) (Narcotic effects) - Category 3 SPECIFIC TARGET ORGAN TOXICITY (REPEATED EXPOSURE) - Category 2 AQUATIC HAZARD (ACUTE) - Category 2 AQUATIC HAZARD (LONG-TERM) - Category 1 GHS label elements Hazard pictograms : Signal word : Danger Hazard statements : Extremely flammable liquid and vapor. May form explosive mixtures in Air. Causes serious eye irritation. Causes skin irritation. May cause respiratory irritation. Suspected of damaging fertility or the unborn child. May cause drowsiness and dizziness. May cause damage to organs through prolonged or repeated exposure. Very toxic to aquatic life with long lasting effects.
    [Show full text]
  • Crude Oil and Fuels
    Name Class Teacher Co-op Academy Leeds Science homework booklet. C14 – Crude oil and fuels Help and support: BBC bitesize for help with this booklet. Or type in the address below: https://www.bbc.co.uk/bitesize/guides/zshvw6f/revision/1 Free GCSE Science lessons: Videos 1 – 5 only: https://www.youtube.com/watch?v=CX2IYWggEBc&list=PL9IouNCPbCxVDcgWiviYYWj0xKMPX Td8s&index=1 Oakwood Academy: https://classroom.thenational.academy/units/organic-chemistry-7c58 Revision guides pages 146 - 148 Spec Summary of the specification content Learning outcomes ref. What most candidates should be able to do 4.7.1. ● Crude oil is a finite resource found in rocks. Crude oil is ● Be able to recognise substances as alkanes 1 the remains of an ancient biomass consisting mainly of given their formulae in these forms. plankton that was buried in mud. ● Students do not need to know the names of ​ ​ ● Crude oil is a mixture of a very large number of specific alkanes other than methane, ethane, compounds. Most of the compounds in crude oil are propane and butane. hydrocarbons, which are molecules made up of hydrogen and carbon atoms only. ● Most of the hydrocarbons in crude oil are hydrocarbons called alkanes. The general formula for the homologous series of alkanes is CnH2n+2 ● The first four members of the alkanes are methane, ethane, propane and butane. ● Alkane molecules can be represented in the following forms: ● C2H6 or 4.7.1. ● The many hydrocarbons in crude oil may be separated ● Explain how fractional distillation works in 2 into fractions, each of which contains molecules with a terms of evaporation and condensation.
    [Show full text]
  • Download English-US Transcript (PDF)
    MITOCW | MIT3_091SCF10lec27_iPOD The following content is provided under a creative commons license. Your support will help MIT OpenCourseWare continue to offer high-quality educational resources for free. To make a donation or view additional materials from hundreds of MIT courses, visit MIT OpenCourseWare at ocw.mit.edu. PROFESSOR: OK. Couple of announcements. First of all, the Wolf Lecture is tomorrow, right here in 10-250 at 4:00. As also, there will be the weekly quiz, the mini celebration. But there's going to be, a week from today, celebration part trois. Yes, third celebration of learning. And remember, what we're shooting for is the smiley face. None of this. And those of you who are over here on the grade point distribution curve, we want to move you to the right. So I'll say a little bit more later in the week about what the coverage will be. I'll be available for office hours later, and I thought to try to cheer you up, and remind you that studying is not something you do only the night before the exam. You have to be studying on a regular basis. All right? So from the iconic film Ghostbusters, there's this one scene. [FILM PLAYBACK] For a moment, pretend that I don't know anything about metallurgy, engineering, or physics, and just tell me what the hell is going on. You never studied. [END FILM PLAYBACK] You don't want to be a character in that scene. So what are you going to do about it? You're going to study.
    [Show full text]
  • HSPA Substance CAS No. Relationship Compilation
    Hydrocarbon Solvents REACH REGISTRATIONS CAS - EC number relationship This documents is for refence only. It has no legal nor regulator value and does not claim to be complete. version October2018 Reach HSPA Category HSPA Substance Name Registration Related CAS No.(s) Related CAS No.(s) Substance Name provisional EC No. Solvent naphtha (petroleum), light C9 Aromatics Hydrocarbons, C9, aromatics 918-668-5 64742-95-6 aromatic Hydrocarbons, C10, Solvent naphtha (petroleum), heavy C10-12 Aromatics 919-284-0 64742-94-5 aromatics, >1% naphthalene aromatic Hydrocarbons, C10, Solvent naphtha (petroleum), heavy C10-12 Aromatics 918-811-1 64742-94-5 aromatics, <1% naphthalene aromatic Hydrocarbons, C10-C13, Solvent naphtha (petroleum), heavy C10-12 Aromatics 922-153-0 64742-94-5 aromatics, <1% naphthalene aromatic Hydrocarbons, C10-C13, Solvent naphtha (petroleum), heavy C10-12 Aromatics 926-273-4 64742-94-5 aromatics, >1% naphthalene aromatic Hydrocarbons, C9-C10, n- C9-14 Aliphatics (2-25% Naphtha (petroleum), alkanes, isoalkanes, cyclics, 927-344-2 64742-82-1 aromatics) hydrodesulfurized heavy aromatics (2- 25%) Hydrocarbons, C10-C13, n- C9-14 Aliphatics (2-25% Naphtha (petroleum), alkanes, isoalkanes, cyclics, 919-164-8 64742-82-1 aromatics) hydrodesulfurized heavy aromatics (2- 25%) Naphtha (petroleum), Hydrocarbons, C8-12, n- C9-14 Aliphatics (2-25% hydrodesulfurized heavy; Low alkanes, isoalkanes, cyclics, 928-136-4 64742-82-1 aromatics) boiling point hydrogen treated aromatics (2- 25%) naphtha Naphtha (petroleum), Hydrocarbons, C9-C12,
    [Show full text]
  • CAS # IUPAC Name/Chemical Name
    CAS # IUPAC Name/Chemical Name/Essenal Oil CAS, Common Name 57-10-3 Hexadecanoic acid Palmi&c acid, natural 57-55-6 Propane-1,2-diol Propylene glycol 59-02-9 (2R)-2,5,7,8-Tetramethyl-2-[(4R,8R)-4,8,12-trimethyltridecyl]-3,4-dihydrochromen-6-ol α-Tocopherol 60-12-8 2-Phenylethanol Phenylethyl alcohol 64-17-5 Ethanol Ethyl alcohol 64-18-6 Methanoic acid Formic acid 64-19-7 Ethanoic acid Ace&c acid 65-85-0 Benzoic acid Benzoic acid 66-25-1 Hexanal C-6 Aldehyde 67-63-0 Propan-2-ol 2-Propanol 67-64-1 Propan-2-one 2-Propanone 75-07-0 Acetaldehyde Acetaldehyde 75-18-3 Methylsulfanylmethane Dimethyl sulfide 75-65-0 2-Methyl-propan-2-ol 2-Methyl-2-propanol 76-22-2 1,7,7-Trimethylbicyclo[2.2.1]heptan-2-one Camphor 77-53-2 (1S,2R,5S,7R,8R)-2,6,6,8-Tetramethyltricyclo[5.3.1.0(1,5)]undecan-8-ol Cedrol 77-54-3 (1S,2R,5S,8R)-2,6,6,8-Tetramethyltricyclo[5.3.1.0(1,5)]undecan-8-yl acetate Cedarwood oil acetylated 77-83-8 Ethyl 3-methyl-3-phenyloxirane-2-carboxylate Ethyl methylphenylglycidate 77-90-7 1,2,3-Tributyl 2-(acetyloxy)propane-1,2,3-tricarboxylate Tributyl o-acetylcitrate 77-92-9 3-Carboxy-3-hydroxypentanedioic acid Citric acid; 2-Hydroxypropane-1,2,3-tricarboxylic acid 77-93-0 1,2,3-Triethyl 2-hydroxypropane-1,2,3-tricarboxylate Triethyl citrate 78-35-3 3,7-Dimethylocta-1,6-dien-3-yl 2-methylpropanoate Linalyl isobutyrate 78-36-4 3,7-Dimethylocta-1,6-dien-3-yl butanoate 1-Ethenyl-1,5-dimethyl-4-hexen-1-yl butanoate 78-37-5 3,7-Dimethylocta-1,6-dien-3-yl (E)-3-phenylprop-2-enoate Linalyl cinnamate 78-69-3 3,7-Dimethyloctan-3-ol Tetrahydrolinalool
    [Show full text]
  • Extended Hard-Sphere Model for Predicting the Viscosity of Long
    Extended Hard-Sphere Model for Predicting the Viscosity of long- chain n-alkanes Nicolas Riesco,1,2 and Velisa Vesovic*,1 1. Department of Earth Science and Engineering, Imperial College London, South Kensington Campus, London SW7 2AZ, United Kingdom. 2 Qatar Carbonates and Carbon Storage Research Centre (QCCSRC), Imperial College London, London SW7 2AZ, UK * To whom correspondence should be addressed. E-mail: [email protected] 1 Abstract An extended hard-sphere model is presented that can accurately and reliably predict the viscosity of long chain n-alkanes. The method is based on the hard-sphere model of Dymond and Assael, that makes use of an universal function relating reduced viscosity to reduced volume. The existing expression for the molar core volume is extrapolated to long chain n-alkanes, while the roughness factor is determined from experimental data. A new correlation for roughness factor is developed that allows the extended model to reproduce the available experimental viscosity data on long chain n-alkanes up to tetracontane (n- C40H82) within ±5 %, at pressure up to 30 MPa. In the dilute gas limit a physically realistic model, based on Lennard-Jones effective potential, is proposed and used to evaluate the zero-density viscosity of n-alkanes to within ±2.4 %, that is better than currently available. Keywords Alkanes; Correlation; Hard-Sphere Theory; High Pressure; Liquid; Vapour; Viscosity. 2 1. Introduction Normal, paraffinic alkanes (n-alkanes) of generic chemical formula CnH2n+2 are an important constituent of oil and are ubiquitous in petroleum and chemical processes. In numerous industrial applications that involve the flow of fluids, knowledge of the viscosity of n-alkanes and their mixtures is an essential pre-requisite for good design and optimal operations [1-2].
    [Show full text]
  • Introduction to Alkanes Alkanes Do Not React with Most Reagents for Two
    Introduction to Alkanes Alkanes do not react with most reagents for two reasons. First, carbon-carbon and carbon-hydrogen single bonds are very strong due to good orbital overlap. Second, the carbon-hydrogen bonds make alkane molecules neither acidic nor basic because the electronegativity of both elements is very similar. This similarity gives the carbonhydrogen bond little polarity, and without polarity, proton loss is difficult. Thus, alkanes make poor acids. Likewise, a lack of nonbonded electron pairs on either the carbon or hydrogen atoms makes alkanes poor bases. However, under proper conditions, alkanes can react with halogens and oxygen. Alkanes: Preparations Alkanes are rarely prepared from other types of compounds because of economic reasons. However, ignoring financial considerations, alkanes can be prepared from the following compounds: 1. Unsaturated compounds via catalytic reduction 2. Alkyl halides via coupling (Wurtz reaction) 3. Alkyl halides via Grignard reagent 4. Alkyl halides via reduction Alkanes: Halogenation The reaction of a halogen with an alkane in the presence of ultraviolet (UV) light or heat leads to the formation of a haloalkane (alkyl halide). An example is the chlorination of methane. Experiments have shown that when the alkane and halogen reactants are not exposed to UV light or heat, the reaction does not occur. However, once a reaction is started, the light or heat source can be removed and the reaction will continue. The mechanism of the reaction explains this phenomenon. Halogenation mechanism. In the methane molecule, the carbon-hydrogen bonds are low-polarity covalent bonds. The halogen molecule has a nonpolar covalent bond. UV light contains sufficient energy to break the weaker nonpolar chlorine-chlorine bond (58 kcal/mole), but it has insufficient energy to break the stronger carbon-hydrogen bond (104 kcal/mole).
    [Show full text]
  • Short Summary of IUPAC Nomenclature of Organic Compounds
    Short Summary of IUPAC Nomenclature of Organic Compounds Introduction The purpose of the IUPAC system of nomenclature is to establish an international standard of naming compounds to facilitate communication. The goal of the system is to give each structure a unique and unambiguous name, and to correlate each name with a unique and unambiguous structure. I. Fundamental Principle IUPAC nomenclature is based on naming a molecule’s longest chain of carbons connected by single bonds, whether in a continuous chain or in a ring. All deviations, either multiple bonds or atoms other than carbon and hydrogen, are indicated by prefixes or suffixes according to a specific set of priorities. II. Alkanes and Cycloalkanes Alkanes are the family of saturated hydrocarbons, that is, molecules containing carbon and hydrogen connected by single bonds only. These molecules can be in continuous chains (called linear or acyclic), or in rings (called cyclic or alicyclic). The names of alkanes and cycloalkanes are the root names of organic compounds. Beginning with the five-carbon alkane, the number of carbons in the chain is indicated by the Greek or Latin prefix. Rings are designated by the prefix “cyclo”. (In the geometrical symbols for rings, each apex represents a carbon with the number of hydrogens required to fill its valence.) CH4 methane CH3[CH2]10CH3 dodecane CH3CH3 ethane CH3[CH2]11CH3 tridecane CH3CH2CH3 propane CH3[CH2]12CH3 tetradecane CH3[CH2]2CH3 butane CH3[CH2]18CH3 icosane CH3[CH2]3CH3 pentane CH3[CH2]19CH3 henicosane CH3[CH2]4CH3 hexane CH3[CH2]20CH3 docosane CH3[CH2]5CH3 heptane CH3[CH2]21CH3 tricosane CH3[CH2]6CH3 octane CH3[CH2]28CH3 triacontane CH3[CH2]7CH3 nonane CH3[CH2]29CH3 hentriacontane CH3[CH2]8CH3 decane CH3[CH2]38CH3 tetracontane CH3[CH2]9CH3 undecane CH3[CH2]48CH3 pentacontane H H C H H C C cyclopropane H H cyclobutane cyclopentane cyclohexane cycloheptane cyclooctane Short Summary of IUPAC Nomenclature, p.
    [Show full text]