Extended Hard-Sphere Model for Predicting the Viscosity of Long
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Section 13. Disposal Considerations Disposal Methods : the Generation of Waste Should Be Avoided Or Minimized Wherever Possible
SAFETY DATA SHEET Flammable Liquid Mixture: Docosane / Dodecane / Dotriacontane / Eicosane / Heptane / Hexacosane / Hexadecane / Hexane / N-Decane / N-Nonane / N- Octadecane / Octacosane / Octane / Tetracosane / Tetradecane / Triacontane Section 1. Identification GHS product identifier : Flammable Liquid Mixture: Docosane / Dodecane / Dotriacontane / Eicosane / Heptane / Hexacosane / Hexadecane / Hexane / N-Decane / N-Nonane / N-Octadecane / Octacosane / Octane / Tetracosane / Tetradecane / Triacontane Other means of : Not available. identification Product use : Synthetic/Analytical chemistry. SDS # : 019981 Supplier's details : Airgas USA, LLC and its affiliates 259 North Radnor-Chester Road Suite 100 Radnor, PA 19087-5283 1-610-687-5253 24-hour telephone : 1-866-734-3438 Section 2. Hazards identification OSHA/HCS status : This material is considered hazardous by the OSHA Hazard Communication Standard (29 CFR 1910.1200). Classification of the : FLAMMABLE LIQUIDS - Category 1 substance or mixture SKIN CORROSION/IRRITATION - Category 2 SERIOUS EYE DAMAGE/ EYE IRRITATION - Category 2A TOXIC TO REPRODUCTION (Fertility) - Category 2 TOXIC TO REPRODUCTION (Unborn child) - Category 2 SPECIFIC TARGET ORGAN TOXICITY (SINGLE EXPOSURE) (Narcotic effects) - Category 3 SPECIFIC TARGET ORGAN TOXICITY (REPEATED EXPOSURE) - Category 2 AQUATIC HAZARD (ACUTE) - Category 2 AQUATIC HAZARD (LONG-TERM) - Category 1 GHS label elements Hazard pictograms : Signal word : Danger Hazard statements : Extremely flammable liquid and vapor. May form explosive mixtures in Air. Causes serious eye irritation. Causes skin irritation. Suspected of damaging fertility or the unborn child. May cause drowsiness and dizziness. May cause damage to organs through prolonged or repeated exposure. Very toxic to aquatic life with long lasting effects. Precautionary statements General : Read label before use. Keep out of reach of children. If medical advice is needed, have product container or label at hand. -

Synthetic Turf Scientific Advisory Panel Meeting Materials
California Environmental Protection Agency Office of Environmental Health Hazard Assessment Synthetic Turf Study Synthetic Turf Scientific Advisory Panel Meeting May 31, 2019 MEETING MATERIALS THIS PAGE LEFT BLANK INTENTIONALLY Office of Environmental Health Hazard Assessment California Environmental Protection Agency Agenda Synthetic Turf Scientific Advisory Panel Meeting May 31, 2019, 9:30 a.m. – 4:00 p.m. 1001 I Street, CalEPA Headquarters Building, Sacramento Byron Sher Auditorium The agenda for this meeting is given below. The order of items on the agenda is provided for general reference only. The order in which items are taken up by the Panel is subject to change. 1. Welcome and Opening Remarks 2. Synthetic Turf and Playground Studies Overview 4. Synthetic Turf Field Exposure Model Exposure Equations Exposure Parameters 3. Non-Targeted Chemical Analysis Volatile Organics on Synthetic Turf Fields Non-Polar Organics Constituents in Crumb Rubber Polar Organic Constituents in Crumb Rubber 5. Public Comments: For members of the public attending in-person: Comments will be limited to three minutes per commenter. For members of the public attending via the internet: Comments may be sent via email to [email protected]. Email comments will be read aloud, up to three minutes each, by staff of OEHHA during the public comment period, as time allows. 6. Further Panel Discussion and Closing Remarks 7. Wrap Up and Adjournment Agenda Synthetic Turf Advisory Panel Meeting May 31, 2019 THIS PAGE LEFT BLANK INTENTIONALLY Office of Environmental Health Hazard Assessment California Environmental Protection Agency DRAFT for Discussion at May 2019 SAP Meeting. Table of Contents Synthetic Turf and Playground Studies Overview May 2019 Update ..... -

Sampling Dynamics for Volatile Organic Compounds Using Headspace Solid-Phase Microextraction Arrow for Microbiological Samples
separations Communication Sampling Dynamics for Volatile Organic Compounds Using Headspace Solid-Phase Microextraction Arrow for Microbiological Samples Kevin E. Eckert 1, David O. Carter 2 and Katelynn A. Perrault 1,* 1 Laboratory of Forensic and Bioanalytical Chemistry, Forensic Sciences Unit, Division of Natural Sciences and Mathematics, Chaminade University of Honolulu, 3140 Waialae Ave., Honolulu, HI 96816, USA; [email protected] 2 Laboratory of Forensic Taphonomy, Forensic Sciences Unit, Division of Natural Sciences and Mathematics, Chaminade University of Honolulu, 3140 Waialae Avenue, Honolulu, HI 96816, USA; [email protected] * Correspondence: [email protected] Received: 10 August 2018; Accepted: 27 August 2018; Published: 10 September 2018 Abstract: Volatile organic compounds (VOCs) are monitored in numerous fields using several commercially-available sampling options. Sorbent-based sampling techniques, such as solid-phase microextraction (SPME), provide pre-concentration and focusing of VOCs prior to gas chromatography–mass spectrometry (GC–MS) analysis. This study investigated the dynamics of SPME Arrow, which exhibits an increased sorbent phase volume and improved durability compared to traditional SPME fibers. A volatile reference mixture (VRM) and saturated alkanes mix (SAM) were used to investigate optimal parameters for microbiological VOC profiling in combination with GC–MS analysis. Fiber type, extraction time, desorption time, carryover, and reproducibility were characterized, in addition to a comparison with traditional SPME fibers. The developed method was then applied to longitudinal monitoring of Bacillus subtilis cultures, which represents a ubiquitous microbe in medical, forensic, and agricultural applications. The carbon wide range/polydimethylsiloxane (CWR/PDMS) fiber was found to be optimal for the range of expected VOCs in microbiological profiling, and a statistically significant increase in the majority of VOCs monitored was observed. -

Safety Data Sheet Acc
Page 1/8 Safety Data Sheet acc. to OSHA HCS Printing date 03/18/2019 Reviewed on 03/18/2019 1 Identification · Product identifier · Product Name: EVEN ALK (C16-C36) · Part Number: ENC-EVEN-1K · Application of the substance / the mixture Certified Reference Material · Details of the supplier of the safety data sheet · Manufacturer/Supplier: SPEX CertiPrep, LLC. 203 Norcross Ave, Metuchen, NJ 08840 USA · Information department: product safety department · Emergency telephone number: Emergency Phone Number (24 hours) CHEMTREC (800-424-9300) Outside US: 703-527-3887 2 Hazard(s) identification · Classification of the substance or mixture GHS02 Flame Flam. Liq. 2 H225 Highly flammable liquid and vapor. GHS08 Health hazard Carc. 2 H351 Suspected of causing cancer. GHS07 Acute Tox. 4 H302 Harmful if swallowed. · Label elements · GHS label elements The product is classified and labeled according to the Globally Harmonized System (GHS). · Hazard pictograms GHS02 GHS07 GHS08 · Signal word Danger · Hazard-determining components of labeling: dichloromethane · Hazard statements H225 Highly flammable liquid and vapor. H302 Harmful if swallowed. H351 Suspected of causing cancer. · Precautionary statements Keep away from heat/sparks/open flames/hot surfaces. - No smoking. Use explosion-proof electrical/ventilating/lighting/equipment. Wear protective gloves/protective clothing/eye protection/face protection. If on skin (or hair): Take off immediately all contaminated clothing. Rinse skin with water/shower. Store locked up. Dispose of contents/container in accordance with local/regional/national/international regulations. · Classification system: · NFPA ratings (scale 0 - 4) Health = 1 3 Fire = 3 1 0 Reactivity = 0 (Contd. on page 2) US 48.1.17.1 Page 2/8 Safety Data Sheet acc. -

Managing Health Risks of Solvent
BEST PRACTICE GUIDELINES Managing the Health Risks of Solvent Exposure Managing the Health Risks of Solvent Exposure September 2015 CONTENTS 1 Introduction 5 1.1 SCOPE AND OBJECTIVES 5 2 The regulatory landscape 6 2.1 CAD 6 2.2 REACH 6 2.3 CLP 8 3 Health effects and properties of solvents 9 3.1 EFFECTS OF SOLVENTS VIA SKIN AND EYE CONTACT 9 3.2 EFFECTS VIA INHALATION 10 3.3 CLASSIFICATION AND LABELLING OF SOLVENTS 10 3.4 HAZARD AND RISK 11 4 Exposure scenarios (es) - Basic principles 12 4.1 DEVELOPING AN ES 13 4.2 SOLVENTS MANUFACTURERS MEET THE CHALLENGE OF DEVELOPING ES 13 5 The solvents industry’s approach to REACH 14 5.1 NAMING CONVENTION FOR HYDROCARBON SOLVENTS 14 5.2 DEVELOPMENT OF GENERIC EXPOSURE SCENARIOS (GES) 14 5.2.1 THE USE DESCRIPTOR SYSTEM (UDS) (REF 15) 15 5.2.2 THE ESIG GES LIBRARY 15 6 Exposure limit values for solvents 17 6.1 OELs AND DNELs 17 6.2 INDUSTRY-BASED OELs FOR HYDROCARBON SOLVENTS 18 ManagingFlammability: the Health Risks A safety of Solvent guide Exposurefor users 7 Responsibilities of solvent users 19 8 Role of solvent vapour monitoring 23 9 Key messages 24 10 List of acronyms 25 11 References 28 APPENDIX 1 Overview of control approaches for solvents required by CAD 29 APPENDIX 2 CLP Classification phrases for solvents 30 APPENDIX 3 Hydrocarbon solvents registered under REACH - key data 31 APPENDIX 4 Oxygenated solvents registered under REACH - key data 43 APPENDIX 5 Example ES for a hydrocarbon solvent containing N-Hexane (>5-80%) 50 APPENDIX 6 List of common solvent uses matched to ESIG generic exposure scenario (GES) title with examples of relevant solvent types 53 APPENDIX 7 Mixtures 62 3 Managing the Health Risks of Solvent Exposure DISCLAIMER The information contained in this paper is intended for guidance only and whilst the information is provided in utmost good faith and has been based on the best information currently available, it is to be relied upon at the user’s own risk. -

Certificate of Analysis
National Institute of Standards & Technology Certificate of Analysis Standard Reference Material 2285 Ignitable Liquids Test Mixture This Standard Reference Material (SRM) is intended primarily for use in the calibration of chromatographic instrumentation used for the classification of an ignitable liquid residue. SRM 2285 is a solution of 15 compounds, including even carbon number aliphatic hydrocarbons from hexane to tetracosane, toluene, p-xylene, 2-ethyltoluene, 3-ethyltoluene, and 1,2,4-trimethylbenzene in methylene chloride. A unit of SRM 2285 consists of five 2 mL ampoules, each containing approximately 1.2 mL of solution. Certified Mass Fraction Values: The certified values for the 15 constituents are given in Table 1. These values are based on results obtained from the gravimetric preparation of this solution and from the analytical results determined by using gas chromatography. A NIST certified value is a value for which NIST has the highest confidence in its accuracy in that all known or suspected sources of uncertainty have been investigated or taken into account [1]. Information Concentration Values: Information values for concentrations, expressed as percent volume fractions, are provided in Table 2 for the components. An information value is considered to be a value that will be of interest and use to the SRM user, but insufficient information is available to assess adequately the uncertainty associated with the value or only a limited number of analyses were performed [1]. Expiration of Certification: The certification of SRM 2285 is valid, within the measurement uncertainty specified, until 30 March 2023, provided the SRM is handled and stored in accordance with the instructions given in this certificate (see “Instructions for Handling, Storage, and Use”). -

Adsorption of Light Alkanes on the Surface of Substrates with Varying Symmetry and Composition
University of Tennessee, Knoxville TRACE: Tennessee Research and Creative Exchange Doctoral Dissertations Graduate School 5-2018 Adsorption of Light Alkanes on the Surface of Substrates with Varying Symmetry and Composition Nicholas Allan Strange University of Tennessee Follow this and additional works at: https://trace.tennessee.edu/utk_graddiss Recommended Citation Strange, Nicholas Allan, "Adsorption of Light Alkanes on the Surface of Substrates with Varying Symmetry and Composition. " PhD diss., University of Tennessee, 2018. https://trace.tennessee.edu/utk_graddiss/4967 This Dissertation is brought to you for free and open access by the Graduate School at TRACE: Tennessee Research and Creative Exchange. It has been accepted for inclusion in Doctoral Dissertations by an authorized administrator of TRACE: Tennessee Research and Creative Exchange. For more information, please contact [email protected]. To the Graduate Council: I am submitting herewith a dissertation written by Nicholas Allan Strange entitled "Adsorption of Light Alkanes on the Surface of Substrates with Varying Symmetry and Composition." I have examined the final electronic copy of this dissertation for form and content and recommend that it be accepted in partial fulfillment of the equirr ements for the degree of Doctor of Philosophy, with a major in Chemistry. John Z. Larese, Major Professor We have read this dissertation and recommend its acceptance: Takeshi Egami, Jeffrey D. Kovac, Brian K. Long Accepted for the Council: Dixie L. Thompson Vice Provost and Dean of the Graduate School (Original signatures are on file with official studentecor r ds.) Adsorption of Light Alkanes on the Surface of Substrates with Varying Symmetry and Composition A Dissertation Presented for the Doctor of Philosophy Degree The University of Tennessee, Knoxville Nicholas Allan Strange May 2018 Copyright © 2018 by Nicholas A. -

Advanced Separation Techniques Combined with Mass Spectrometry for Difficult Analytical Tasks - Isomer Separation and Oil Analysis
FINNISH METEOROLOGICAL INSTITUTE Erik Palménin aukio 1 P.O. Box 503 FI-00101 HELSINKI 131 CONTRIBUTIONS tel. +358 29 539 1000 WWW.FMI.FI FINNISH METEOROLOGICAL INSTITUTE CONTRIBUTIONS No. 131 ISBN 978-952-336-016-7 (paperback) ISSN 0782-6117 Erweko Helsinki 2017 ISBN 978-952-336-017-4 (pdf) Helsinki 2017 ADVANCED SEPARATION TECHNIQUES COMBINED WITH MASS SPECTROMETRY FOR DIFFICULT ANALYTICAL TASKS - ISOMER SEPARATION AND OIL ANALYSIS JAAKKO LAAKIA Department of Chemistry University of Helsinki Finland Advanced separation techniques combined with mass spectrometry for difficult analytical tasks – isomer separation and oil analysis Jaakko Laakia Academic Dissertation To be presented, with the permission of the Faculty of Science of the University of Helsinki, for public criticism in Auditorium A129 of the Department of Chemistry (A.I. Virtasen aukio 1, Helsinki) on May 12th, 2017, at 12 o’clock noon. Helsinki 2017 1 TABLE OF CONTENTS ABSTRACT 4 Supervisors Professor Tapio Kotiaho TIIVISTELMÄ 5 Department of Chemistry LIST OF ORIGINAL PAPERS 6 Faculty of Science ACKNOWLEDGEMENTS 7 ABBREVIATIONS 8 and 1. INTRODUCTION 10 Division of Pharmaceutical Chemistry and Technology 1.1.1 Basic operation principles of ion mobility 12 spectrometry 11 Faculty of Pharmacy 1.1.2 Applications of ion mobility spectrometry 16 University of Helsinki 1.2 Basic operation principles and applications of two-dimensional gas 19 chromatography – time-of-flight mass spectrometry Docent Tiina Kauppila 1.3 Aims of study 23 Division of Pharmaceutical Chemistry and Technology -

Safety Data Sheet
SAFETY DATA SHEET Flammable Liquid Mixture: Docosane / Dodecane / Eicosane / Hexacosane / Hexadecane / Hexane / N-Decane / N-Heptane / N-Nonane / N-Octadecane / N- Octane / Octacosane / Tetracosane / Tetradecane Section 1. Identification GHS product identifier : Flammable Liquid Mixture: Docosane / Dodecane / Eicosane / Hexacosane / Hexadecane / Hexane / N-Decane / N-Heptane / N-Nonane / N-Octadecane / N-Octane / Octacosane / Tetracosane / Tetradecane Other means of : Not available. identification Product use : Synthetic/Analytical chemistry. SDS # : 019735 Supplier's details : Airgas USA, LLC and its affiliates 259 North Radnor-Chester Road Suite 100 Radnor, PA 19087-5283 1-610-687-5253 24-hour telephone : 1-866-734-3438 Section 2. Hazards identification OSHA/HCS status : This material is considered hazardous by the OSHA Hazard Communication Standard (29 CFR 1910.1200). Classification of the : FLAMMABLE LIQUIDS - Category 1 substance or mixture SKIN CORROSION/IRRITATION - Category 2 SERIOUS EYE DAMAGE/ EYE IRRITATION - Category 2A TOXIC TO REPRODUCTION (Fertility) - Category 2 TOXIC TO REPRODUCTION (Unborn child) - Category 2 SPECIFIC TARGET ORGAN TOXICITY (SINGLE EXPOSURE) (Respiratory tract irritation) - Category 3 SPECIFIC TARGET ORGAN TOXICITY (SINGLE EXPOSURE) (Narcotic effects) - Category 3 SPECIFIC TARGET ORGAN TOXICITY (REPEATED EXPOSURE) - Category 2 AQUATIC HAZARD (ACUTE) - Category 2 AQUATIC HAZARD (LONG-TERM) - Category 1 GHS label elements Hazard pictograms : Signal word : Danger Hazard statements : Extremely flammable liquid and vapor. May form explosive mixtures in Air. Causes serious eye irritation. Causes skin irritation. May cause respiratory irritation. Suspected of damaging fertility or the unborn child. May cause drowsiness and dizziness. May cause damage to organs through prolonged or repeated exposure. Very toxic to aquatic life with long lasting effects. Precautionary statements General : Read label before use. -

Vapor Pressures and Vaporization Enthalpies of the N-Alkanes from 2 C21 to C30 at T ) 298.15 K by Correlation Gas Chromatography
BATCH: je1a04 USER: jeh69 DIV: @xyv04/data1/CLS_pj/GRP_je/JOB_i01/DIV_je0301747 DATE: October 17, 2003 1 Vapor Pressures and Vaporization Enthalpies of the n-Alkanes from 2 C21 to C30 at T ) 298.15 K by Correlation Gas Chromatography 3 James S. Chickos* and William Hanshaw 4 Department of Chemistry and Biochemistry, University of MissourisSt. Louis, St. Louis, Missouri 63121 5 6 The temperature dependence of gas chromatographic retention times for n-heptadecane to n-triacontane 7 is reported. These data are used to evaluate the vaporization enthalpies of these compounds at T ) 298.15 8 K, and a protocol is described that provides vapor pressures of these n-alkanes from T ) 298.15 to 575 9 K. The vapor pressure and vaporization enthalpy results obtained are compared with existing literature 10 data where possible and found to be internally consistent. Sublimation enthalpies for n-C17 to n-C30 are 11 calculated by combining vaporization enthalpies with fusion enthalpies and are compared when possible 12 to direct measurements. 13 14 Introduction 15 The n-alkanes serve as excellent standards for the 16 measurement of vaporization enthalpies of hydrocarbons.1,2 17 Recently, the vaporization enthalpies of the n-alkanes 18 reported in the literature were examined and experimental 19 values were selected on the basis of how well their 20 vaporization enthalpies correlated with their enthalpies of 21 transfer from solution to the gas phase as measured by gas 22 chromatography.3 A plot of the vaporization enthalpies of 23 the n-alkanes as a function of the number of carbon atoms 24 is given in Figure 1. -
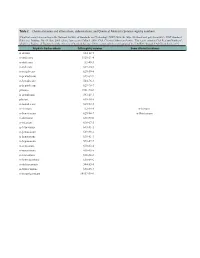
Table 2. Chemical Names and Alternatives, Abbreviations, and Chemical Abstracts Service Registry Numbers
Table 2. Chemical names and alternatives, abbreviations, and Chemical Abstracts Service registry numbers. [Final list compiled according to the National Institute of Standards and Technology (NIST) Web site (http://webbook.nist.gov/chemistry/); NIST Standard Reference Database No. 69, June 2005 release, last accessed May 9, 2008. CAS, Chemical Abstracts Service. This report contains CAS Registry Numbers®, which is a Registered Trademark of the American Chemical Society. CAS recommends the verification of the CASRNs through CAS Client ServicesSM] Aliphatic hydrocarbons CAS registry number Some alternative names n-decane 124-18-5 n-undecane 1120-21-4 n-dodecane 112-40-3 n-tridecane 629-50-5 n-tetradecane 629-59-4 n-pentadecane 629-62-9 n-hexadecane 544-76-3 n-heptadecane 629-78-7 pristane 1921-70-6 n-octadecane 593-45-3 phytane 638-36-8 n-nonadecane 629-92-5 n-eicosane 112-95-8 n-Icosane n-heneicosane 629-94-7 n-Henicosane n-docosane 629-97-0 n-tricosane 638-67-5 n-tetracosane 643-31-1 n-pentacosane 629-99-2 n-hexacosane 630-01-3 n-heptacosane 593-49-7 n-octacosane 630-02-4 n-nonacosane 630-03-5 n-triacontane 638-68-6 n-hentriacontane 630-04-6 n-dotriacontane 544-85-4 n-tritriacontane 630-05-7 n-tetratriacontane 14167-59-0 Table 2. Chemical names and alternatives, abbreviations, and Chemical Abstracts Service registry numbers.—Continued [Final list compiled according to the National Institute of Standards and Technology (NIST) Web site (http://webbook.nist.gov/chemistry/); NIST Standard Reference Database No. -

Section 2. Hazards Identification OSHA/HCS Status : This Material Is Considered Hazardous by the OSHA Hazard Communication Standard (29 CFR 1910.1200)
SAFETY DATA SHEET Flammable Liquid Mixture: Docosane / Dodecane / Eicosane / Hexadecane / Hexane / N-Decane / N-Heptane / N-Nonane / N-Octadecane / N-Octane / N-Tridecane / Tetracosane / Tetradecane / Undecane Section 1. Identification GHS product identifier : Flammable Liquid Mixture: Docosane / Dodecane / Eicosane / Hexadecane / Hexane / N-Decane / N-Heptane / N-Nonane / N-Octadecane / N-Octane / N-Tridecane / Tetracosane / Tetradecane / Undecane Other means of : Not available. identification Product use : Synthetic/Analytical chemistry. SDS # : 018777 Supplier's details : Airgas USA, LLC and its affiliates 259 North Radnor-Chester Road Suite 100 Radnor, PA 19087-5283 1-610-687-5253 24-hour telephone : 1-866-734-3438 Section 2. Hazards identification OSHA/HCS status : This material is considered hazardous by the OSHA Hazard Communication Standard (29 CFR 1910.1200). Classification of the : FLAMMABLE LIQUIDS - Category 1 substance or mixture SKIN CORROSION/IRRITATION - Category 2 SERIOUS EYE DAMAGE/ EYE IRRITATION - Category 2A TOXIC TO REPRODUCTION (Fertility) - Category 2 TOXIC TO REPRODUCTION (Unborn child) - Category 2 SPECIFIC TARGET ORGAN TOXICITY (SINGLE EXPOSURE) (Respiratory tract irritation) - Category 3 SPECIFIC TARGET ORGAN TOXICITY (SINGLE EXPOSURE) (Narcotic effects) - Category 3 SPECIFIC TARGET ORGAN TOXICITY (REPEATED EXPOSURE) - Category 2 AQUATIC HAZARD (ACUTE) - Category 2 AQUATIC HAZARD (LONG-TERM) - Category 1 GHS label elements Hazard pictograms : Signal word : Danger Hazard statements : Extremely flammable liquid and vapor. May form explosive mixtures in Air. Causes serious eye irritation. Causes skin irritation. May cause respiratory irritation. Suspected of damaging fertility or the unborn child. May cause drowsiness and dizziness. May cause damage to organs through prolonged or repeated exposure. Very toxic to aquatic life with long lasting effects.