DOCSLIB.ORG

Design of Position PID Control Algorithm Deng-Yuan ZENG*, Ling LONG and Jun-Xiang HE Southwest National University of Chengdu, China *Corresponding Author

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Design of Position PID Control Algorithm Deng-Yuan ZENG*, Ling LONG and Jun-Xiang HE Southwest National University of Chengdu, China *Corresponding Author 2017 2nd International Conference on Applied Mechanics and Mechatronics Engineering (AMME 2017) ISBN: 978-1-60595-521-6 Design of Position PID Control Algorithm Deng-yuan ZENG*, Ling LONG and Jun-xiang HE Southwest National University of Chengdu, China *Corresponding author Keyword: Position PID Single Chip Microcomputer Servo Error Last Error KP KD. Abstract. The servo control scheme on the basis of single-chip, this paper presents a solution to a positional PID control algorithm, the algorithm is to control the volume when full output, adding proportional, integral, differential link, the feedback to the output, complete closed-loop Control system to speed up the controlled response rate. Successfully solved in a short time the steering gear to achieve the desired effect, speed up the steering gear response rate. Introduction The steering gear can be said to be integrated with a DC motor, a motor controller and a geared motor, etc., and is packaged with a housing servo unit. Through the input of a fixed frequency of different duty cycle PWM signal to the steering wheel to rotate the more accurate angular displacement of the motor control system. Widely used in various colleges and universities, primary and secondary school robot teaching, but also all small and medium enterprises in the control system of choice. Add positional PID servo control on the control algorithm, when the speed of the system's response to the deviation signal is greatly enhanced, the system greatly reduces the time adjustment, and does not require a large number of complicated theoretical calculation, we do not have precise knowledge of the controlled object precisely of the mathematical model. The Classic PID Analysis For the control of the steering gear can be open-loop control and closed-loop control, open-loop control directly given the desired value, through a period of time, to overcome some of the defects and then slowly set the desired value, or near the expected value, by the outside world The position error can occur when the input unit enters the desired value, so that the current position error can be obtained, so that it can compensate in time and solve the influence of the external environment on the steering angle. Increase, the reaction rate also has a big improvement. The control schematic is as follows among them. Figure 1. PID controller schematic. 1(t de t) uKetetdtT(t) () () pd 0 Tdti Proportion of links - the main amplification output, its role can be expressed as K*ep （ t）; Integral link - the main thing is to integrate the time constant, its role can be expressed as 1 t K*etdt () ; p 0 T i 185 Differential link - mainly on the time constant differential, its role can be expressed as de() t K*T ; p d dt Actuator - for the actuator, that is, the work of the accused unit; this article to the steering gear for the implementation of the unit. Sensor-sensor, such as the speed measurement, the need for photoelectric encoder; measured voltage need to use a voltage divider to collect small voltage. Its role is to pass the feedback signal to the system. Realization of Positional PID Algorithm for Servo The positional PID adds a step signal input to the given PID algorithm and discretizes n T TD Un() Kp {() en ei () [() en en ( 1)]} u0 Tii0 T After simplification, can also be expressed as n u(n)=Kpien ( ) K ek ( ) K d ( en ( ) en ( 1))+u0 k 0 among them KT K T p , K P d K i d T i T With the microcontroller (MK60DN512VLL105N22D) to the steering gear (S3010) input control signal for the servo work generally use 50hz frequency of different duty cycle PWM wave to give the steering gear gives a more accurate angular displacement, here through the program control microcontroller internal PIT The timer generates 300Hz different duty cycle PWM wave to the steering gear to send the angular displacement of the control signal, and then through the position PID to do closed-loop control. C language program Val uint16 SetVal Kp * Error Kd * Error Last_ Error ; where Val is the final output value, SetVal is the set value, and then the current error is calculated at the end of the program. Error = Expected value - Output value , And then the current error in the calculation assigned to the last error LastError Error ; KP is proportional to the controller, in fact, is proportional to the adjustable controller can be adjusted, that is, Val KP * Error ; where KP for the proportional gain can be greater than 1, but also can be less than 1; where KP larger, the controller magnification The larger the curve of the controlled parameter, the smaller the KP, the smaller the magnification of the controller, and the smoother the curve of the controlled parameter. But at the same time the proportion of the controller will introduce the role of surplus, to eliminate the influence of the surplus to introduce the integral link KI. KI is the integrator, the integral is accumulated over time, and then the introduction of the error to accumulate, that is, when the measured value and set the value of error when the integrator will continue to accumulate the deviation over time. The integrator will only stop when Error is 0. Val KP * Error KI * Error , KI * Error is the output caused by the integrator. The smaller the integration time is, the higher the integral is, the stronger the integral effect is. The larger the integration time is, the smaller the integral speed is, and the weaker the integral effect. KD is a differential controller, mainly used to overcome the lagging problem of the controlled object, differential output and differential time and deviation changes and the deviation does not matter. The longer the deviation rate is, the longer the derivative time is, the greater the differential output is caused, and if the differential effect is too strong, the controller will produce significant "spikes" and "mutations". 186 Analysis of Positional PID Algorithm Control In the control of the steering gear analysis of the response Figure 2. P controller response curve. Figure 3. PI controller response curve. Figure 4. PD controller response curve. Figure 5. PID controller response curve. P Controller Diagram Response Curve (Figure2) Shows that only in the proportion of links, the proportion of links is to amplify the error signal to improve the sensitivity of the controller on the error signal, with no distortion, no delay, proportional amplification of the input signal with the characteristics of the signal changes over time. But too large Kp will appear system shock and divergence, the system becomes unstable, increase the overshoot; PI Controller Diagram Response Curve (Figure3) Shows that the proportion of links to join the integral part of the elimination of residual. Integral link can play a part of the memory function, it can accumulate the error, so that the control signal of the controller continue to increase until the error is 0, will stop working, eliminating the system deviation; PD Controller Response Curve (Figure4) Diagram shows that in the differential link, it changes the trend of the system to the controller output control signal, the system can make a large change in the advance correction signal, greatly reduce the overshoot, so that the system response rate has been greatly improved. PID Controller Diagram Response Curve (Figure5) Can be obtained. After the positional PID control algorithm is added to the steering control system, the performance of the system has been greatly improved. The system is not distorted and 187 improved at the corresponding rate, and the system is eliminated. Residuals, so that the system can overcome the external factors to achieve the desired results. Conclusion After the test, in the control of the servo on the position of the PID, the rapid response to the servo on the algorithm to control, in a short time to allow the servo control system to be handled accordingly, greatly speed up the rudder reaction speed, So that the steering gear can be in a short time to achieve "stable fast." Acknowledgements This work was financially supported by the Fundamental Research Funds for the Central Universities of Southwest University for Nationalities (NO.20 16NZYQN08). Reference [1] Wang Q.G., Hang C.C., Yang X.P. PID controller design via IMC principles[C]// Control Conference. IEEE, 2015: 514-521. [2] Panagopoulos H., Åström, Karl J. PID control design and ℋ∞ loop shaping [J]. International Journal of Robust & Nonlinear Control, 2015, 10(15): 1249-1261.] [3] Shah P., Agashe S. Review of fractional PID controller [J]. Mechatronics, 2016, 38:29-41. [4] Freire H.F., Oliveira P.B.D.M., Pires E J S, et al. Many-Objective PSO PID Controller Tuning [J]. Lecture Notes in Electrical Engineering, 2015, 321:183-192. [5] Maheshappa H.D., Samuel R.D.S., Prakashan A. Digital PID Controller for Speed Control of DC Motors [J]. Iete Technical Review, 2015, 6(3): 171-176.] [6] Vishal, Ohri J. G.A. tuned LQR and PID controller for aircraft pitch control [C]// IEEE, India International Conference on Power Electronics. IEEE, 2015: 1-6. [7] Liu L., Pan F., Xue D. Variable-order fuzzy fractional PID controller. [J]. Isa Transactions, 2015, 55: 227. [8] Hwang S.H., Shiu S.J., Lin M.L. PID control of unstable systems having time delay[C]// Control Conference. IEEE, 2015: 2162-2167. [9] Garrido J., Vázquez F., Morilla F. Multivariable PID control by decoupling [J]. International Journal of Systems Science, 2016, 10(1): 1-19. [10] Taeib A., Chaari A. Tuning optimal P.I.D. controller [J]. International Journal of Modelling Identification & Control, 2015, 23(2): 140.
Load more

Recommended publications
  • Tianjin Travel Guide
    Tianjin Travel Guide Travel in Tianjin Tianjin (tiān jīn 天津), referred to as "Jin (jīn 津)" for short, is one of the four municipalities directly under the Central Government of China. It is 130 kilometers southeast of Beijing (běi jīng 北京), serving as Beijing's gateway to the Bohai Sea (bó hǎi 渤海). It covers an area of 11,300 square kilometers and there are 13 districts and five counties under its jurisdiction. The total population is 9.52 million. People from urban Tianjin speak Tianjin dialect, which comes under the mandarin subdivision of spoken Chinese. Not only is Tianjin an international harbor and economic center in the north of China, but it is also well-known for its profound historical and cultural heritage. History People started to settle in Tianjin in the Song Dynasty (sòng dài 宋代). By the 15th century it had become a garrison town enclosed by walls. It became a city centered on trade with docks and land transportation and important coastal defenses during the Ming (míng dài 明代) and Qing (qīng dài 清代) dynasties. After the end of the Second Opium War in 1860, Tianjin became a trading port and nine countries, one after the other, established concessions in the city. Historical changes in past 600 years have made Tianjin an unique city with a mixture of ancient and modem in both Chinese and Western styles. After China implemented its reforms and open policies, Tianjin became one of the first coastal cities to open to the outside world. Since then it has developed rapidly and become a bright pearl by the Bohai Sea.
    [Show full text]
  • Deng Xiaoping in the Making of Modern China
    Teaching Asia’s Giants: China Crossing the River by Feeling the Stones Deng Xiaoping in the Making of Modern China Poster of Deng Xiaoping, By Bernard Z. Keo founder of the special economic zone in China in central Shenzhen, China. he 9th of September 1976: The story of Source: The World of Chinese Deng Xiaoping’s ascendancy to para- website at https://tinyurl.com/ yyqv6opv. mount leader starts, like many great sto- Tries, with a death. Nothing quite so dramatic as a murder or an assassination, just the quiet and unassuming death of Mao Zedong, the founding father of the People’s Republic of China (PRC). In the wake of his passing, factions in the Chinese Communist Party (CCP) competed to establish who would rule after the Great Helmsman. Pow- er, after all, abhors a vacuum. In the first corner was Hua Guofeng, an unassuming functionary who had skyrocketed to power under the late chairman’s patronage. In the second corner, the Gang of Four, consisting of Mao’s widow, Jiang September 21, 1977. The Qing, and her entourage of radical, leftist, Shanghai-based CCP officials. In the final corner, Deng funeral of Mao Zedong, Beijing, China. Source: © Xiaoping, the great survivor who had experi- Keystone Press/Alamy Stock enced three purges and returned from the wil- Photo. derness each time.1 Within a month of Mao’s death, the Gang of Four had been imprisoned, setting up a showdown between Hua and Deng. While Hua advocated the policy of the “Two Whatev- ers”—that the party should “resolutely uphold whatever policy decisions Chairman Mao made and unswervingly follow whatever instructions Chairman Mao gave”—Deng advocated “seek- ing truth from facts.”2 At a time when China In 1978, some Beijing citizens was reexamining Mao’s legacy, Deng’s approach posted a large-character resonated more strongly with the party than Hua’s rigid dedication to Mao.
    [Show full text]
  • The Aesthetic Activity in Modern Fiction
    Can Xue Interview The Aesthetic Activity in Modernist Fiction Can Xue (Deng Xiaohua), whose pseudonym in Chinese means both the dirty snow that refuses to melt and the purest snow at the top of a high mountain, was born in 1953 in Changsha City, Hunan Province, in South China. She lived in Changsha until 2001, when she and her husband moved to Beijing. In 1957, her father, an editorial director at the New Hunan Daily News, was condemned as an Ultra-Rightist and was sent to reform through labor, and her mother, who worked at the same newspaper, was sent to the countryside for labor as well. Because of the family catastrophe during the Cultural Revolution, Can Xue lost her chance for further education and only graduated from elementary school. Largely self-taught, she loved literature so much that she read fiction and poetry whenever she could. In her younger days, she liked classical Western literature and Russian literature the best, and they remain her favorites today. Can Xue has studied reading and writing in English for years, and she has read extensively English texts of literature. Can Xue, who describes her works as “soul literature" or "life literature," is the author of numerous short-story collections and four novels. Five of her works have been published in English, including Dialogues in Paradise (Northwestern University Press, 1989), Old Floating Cloud: Two Novelllas (Northwestern University Press, 1991), The Embroidered Shoes (Henry Holt, 1997), Blue Light in the Sky and Other Stories (New Directions, 2006), and Five Spice Street (Yale University Press, 2009).
    [Show full text]
  • Self-Study Syllabus on China’S Domestic Politics
    Self-Study Syllabus on China’s domestic politics www.mandarinsociety.org PrefaceAbout this syllabus. syllabus aspires to guide interested non-specialists in Thisthe study of some of the most salient and important aspects of the contemporary Chinese domestic political scene. The recommended readings survey basic features of China’s political system as well as important developments in politics, ideology, and domestic policy under Xi Jinping. Some effort has been made to promote awareness of the broad array of available English language scholarship and analysis. Reflecting the authors’ belief that study of official documents remains a critical skill for the study of Chinese politics, an effort has been made as well to include some of these important sources. This syllabus is organized to build understanding in a step-by-step fashion based on one hour of reading five nights a week for four weeks. We assume at most a passing familiarity with the Chinese political system. The syllabus also provides a glossary of key terms and a list of recommended reading for books and websites for those seeking to engage in deeper study. American Mandarin Society 1 Week One: Building the Foundation The organization, ideology, and political processes of China’s governance • “Chinese Politics Has No Rules, But It May Be Good if Xi Jinping Breaks Them” Overview ,Christopher Johnson, Center for Strategic and International Studies, August 9, 2017. Mr. Johnson argues that the institutionalization of This week’s readings review some of the basic and most distinctive features of China’s Chinese politics was less than many foreign political system.
    [Show full text]
  • D~-Zeng, Deng Zeng-Jie and Zhou Hui- Jiu 1
    D~-Zeng,Deng Zeng-Jie and Zhou Hui- Jiu %efailure and the prevention of failure of elevator links for oil well drilling have been ,yestigated.After presenting a failure analysis of elevator links, a fracture mechanics approach $4for computing the fracture strength and residual life is described, and the results are omparedwith those obtained by fatigue tests of actual links. Finally, the effect of shot-peening ,the fatigue lives of elevator links is discussed. lay words: fatigue; fatigue life prediction; shot-peening; fracture analysis; elevator links elevator link is an important implement in oil drilling: ran elevator link breaks a catastrophic accident may ccur. It is necessary to reduce the weight of elevator links nd to prolong their service life to facilitate drilling opera- ons and to ensure safety. We have developed a low-carbon lartensitic steel, 0. 2C-Si-Mn-Mo-V,with high strength, uctility and fracture toughness, which has been used ltisfactorily for making all kinds of light-weight elevator nks in the People's Republic of China. The weight of these evator links is much less than that of conventional links, but in recent years there have been occasional reports of fracture of these light-weight links after a period of service, apparently due to fatigue. On the basis of failure analysis we have adopted a / fracture mechanics approach dealing with the link as a cracked body and have compared the results of calculations , of critical crack length and residual life with those deter- mined from monitoring the links during service. Finally we have applied shot-peening to overcome the effect of surface defects, further ensuring safety and prolonging the service life of the elevator links.
    [Show full text]
  • Huaqiang ZENG Team Leader and Principal Research Scientist
    Huaqiang ZENG Team Leader and Principal Research Scientist +65 6824 7115 [email protected] Team Leader and Principal Research Scientist, NanoBio Lab, Singapore, 2019-present Team Leader and Principal Research Scientist, Institute of Bioengineering and Nanotechnology, Singapore, 2014-2019 Assistant Professor, National University of Singapore, 2006-2013 Postdoctoral Research Fellow, The Scripps Research Institute, USA, 2002-2006 Ph.D. in Organic Chemistry, The State University of New York at Buffalo, USA, 2002 B.S. in Chemical Physics, The University of Science and Technology of China, 1996 Publications 1. A. Roy, H. Joshi, R. Ye, J. Shen, F. Chen, A. Aksimentiev and H. Zeng, “Polyhydrazide‐Based Organic Nanotubes as Efficient and Selective Artificial Iodide Channels,” Angewandte Chemie International Edition, 132 (2020) 4836-4843. IF 12.102 2. J. Shen, J. Fan, R. Ye, N. Li, Y. Mu and H. Zeng, “Polypyridine-Based Helical Amide Foldamer Channels for Rapid Transport of Water and Proton with High Ion Rejection,” Angewandte Chemie International Edition, (2020) DOI: 10.1002/anie.202003512. IF 12.257 3. J. Shen, R. Ye, A. Romanies, A. Roy, F. Chen, C. Ren, Z. Liu and H. Zeng, “An Aquafoldmer-Based Aquaporin-Like Synthetic Water Channel,” Journal of the American Chemical Society, 142 (2020) 10050-10058. IF 14.695 4. H. Zeng, A. Roy, H. Joshi, R. Ye, J. Shen, F. Chen and A. Aksimentiev, “Polyhydrazide-Based Organic Nanotubes as Extremely Efficient and Highly Selective Artificial Iodide Channels,” Angew. Chem. Int. Ed., (2020) DOI: 10.1002/anie.201916287 5. H. Zeng, F. Chen, J. Shen, N. Li, A.
    [Show full text]
  • China's Special Economic Zones And
    China’s Special Economic Zones and Industrial Clusters: Success and Challenges Douglas Zhihua Zeng © 2012 Lincoln Institute of Land Policy Lincoln Institute of Land Policy Working Paper The findings and conclusions of this Working Paper reflect the views of the author(s) and have not been subject to a detailed review by the staff of the Lincoln Institute of Land Policy. Contact the Lincoln Institute with questions or requests for permission to reprint this paper. [email protected] Lincoln Institute Product Code: WP13DZ1 Abstract In the past 30 years, China has achieved phenomenal economic growth, an unprecedented development “miracle” in human history. How did China achieve this rapid growth? What have been its key drivers? And, most important, can China sustain the incredible success? While policy makers, business people, and scholars continue to debate these topics, one thing is clear: the numerous special economic zones and industrial clusters that emerged after the country’s reforms are without doubt two important engines of China’s remarkable development. The special economic zones and industrial clusters have made crucial contributions to China’s economic success. Foremost, the special economic zones (especially the first several) successfully tested the market economy and new institutions and became role models for the rest of the country to follow. Together with the numerous industrial clusters, the special economic zones have contributed significantly to gross domestic product, employment, exports, and attraction of foreign investment. The special economic zones have also played important roles in bringing new technologies to China and in adopting modern management practices. However, after 30 years’ development, they also face many significant challenges in moving forward.
    [Show full text]
  • DENG Guo (邓 国) , ZHOU Yu-Shu (周玉淑) , LIU Li-Ping (刘黎平) 1
    Vol.16 No.2 JOURNAL OF TROPICAL METEOROLOGY June 2010 Article ID: 1006-8775(2010) 02-0154-06 USE OF A NEW STEERING FLOW METHOD TO PREDICT TROPICAL CYCLONE MOTION 1 2 3 DENG Guo (邓 国), ZHOU Yu-shu (周玉淑) , LIU Li-ping (刘黎平) (1. National Meteorological Center, Beijing 100081 China; 2. Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029 China; 3. Chinese Academy of Meteorological Sciences, Beijing 100081 China) Abstract: A tropical cyclone is a kind of violent weather system that takes place in warmer tropical oceans and spins rapidly around its center and at the same time moves along surrounding flows. It is generally recognized that the large-scale circulation plays a major role in determining the movement of tropical cyclones and the effects of steering flows are the highest priority in the forecasting of tropical cyclone motion and track. This article adopts a new method to derive the steering flow and select a typical swerving track case (typhoon Dan, coded 9914) to illustrate the validity of the method. The general approach is to modify the vorticity, geostropical vorticity and divergence, investigate the change in the non-divergent stream function, geoptential and velocity potential, respectively, and compute a modified velocity field to determine the steering flow. Unlike other methods in regular use such as weighted average of wind fields or geopoential height, this method has the least adverse effects on the environmental field and could derive a proper steering flow which fits well with storm motion. Combined with other internal and external forcings, this method could have wide application in the prediction of tropical cyclone track.
    [Show full text]
  • Origin Narratives: Reading and Reverence in Late-Ming China
    Origin Narratives: Reading and Reverence in Late-Ming China Noga Ganany Submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the Graduate School of Arts and Sciences COLUMBIA UNIVERSITY 2018 © 2018 Noga Ganany All rights reserved ABSTRACT Origin Narratives: Reading and Reverence in Late Ming China Noga Ganany In this dissertation, I examine a genre of commercially-published, illustrated hagiographical books. Recounting the life stories of some of China’s most beloved cultural icons, from Confucius to Guanyin, I term these hagiographical books “origin narratives” (chushen zhuan 出身傳). Weaving a plethora of legends and ritual traditions into the new “vernacular” xiaoshuo format, origin narratives offered comprehensive portrayals of gods, sages, and immortals in narrative form, and were marketed to a general, lay readership. Their narratives were often accompanied by additional materials (or “paratexts”), such as worship manuals, advertisements for temples, and messages from the gods themselves, that reveal the intimate connection of these books to contemporaneous cultic reverence of their protagonists. The content and composition of origin narratives reflect the extensive range of possibilities of late-Ming xiaoshuo narrative writing, challenging our understanding of reading. I argue that origin narratives functioned as entertaining and informative encyclopedic sourcebooks that consolidated all knowledge about their protagonists, from their hagiographies to their ritual traditions. Origin narratives also alert us to the hagiographical substrate in late-imperial literature and religious practice, wherein widely-revered figures played multiple roles in the culture. The reverence of these cultural icons was constructed through the relationship between what I call the Three Ps: their personas (and life stories), the practices surrounding their lore, and the places associated with them (or “sacred geographies”).
    [Show full text]
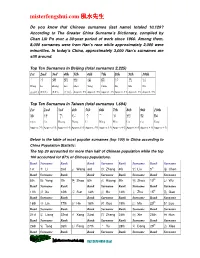
  • Misterfengshui.Com 風水先生
    misterfengshui.com 風水先生 Do you know that Chinese surnames (last name) totaled 10,129? According to The Greater China Surname’s Dictionary, compiled by Chan Lik Pu over a 30-year period of work since 1960. Among them, 8,000 surnames were from Han’s race while approximately 2,000 were minorities. In today’s China, approximately 3,000 Han’s surnames are still around. Top Ten Surnames In Beijing (total surnames 2,225) 1st 2nd 3rd 4th 5th 6th 7th 8th 9th 10th 王 李 張 劉 趙 楊 陳 徐 馬 吳 Wang Li Zhang Liu Zhao Yang Chen Xu Ma Wu (10.6% ) (9.6%) (9.6%) (7.7% ) Approx. 5% Approx. 5% Approx. 4% Approx. 4% Approx. 4% Approx. 3% Top Ten Surnames In Taiwan (total surnames 1,694) 1st 2nd 3rd 4th 5th 6th 7th 8th 9th 10th 陳 林 黃 張 李 王 吳 劉 蔡 楊 Chen Lin Huang Zhang Li Wang Wux. Liu Cai Yang Approx .7% Approx 6 % Approx 6 % Approx 6 % Approx. 5% Approx 5 % Approx 4 % Approx 4 % Approx 4 % Approx 4 % Below is the table of most popular surnames (top 100) in China according to China Population Statistic: The top 20 accounted for more than half of Chinese population while the top 100 accounted for 87% of Chinese populations. Rank Surname Rank Rank Surname Rank Surname Rank Surname 1st 李 Li 2nd 王 Wang 3rd 張 Zhang 4th 劉 Liu 5th 陳 Chen Rank Surname Rank Rank Surname Rank Surname Rank Surname 6th 楊 Yang 7th 趙 Zhao 8th 黃 Huang 9th 周 Zhou 10 th 吳 Wu Rank Surname Rank Rank Surname Rank Surname Rank Surname 11th 徐 Xu 12th 孫 Sun 13th 胡 Hu 14th 朱 Zhu 15 th 高 Gao Rank Surname Rank Rank Surname Rank Surname Rank Surname 16th 林 Lin 17th 何 He 18th 郭 Guo 19th 馬 Ma 20 th 羅 Luo Rank
    [Show full text]
  • Representing Talented Women in Eighteenth-Century Chinese Painting: Thirteen Female Disciples Seeking Instruction at the Lake Pavilion
    REPRESENTING TALENTED WOMEN IN EIGHTEENTH-CENTURY CHINESE PAINTING: THIRTEEN FEMALE DISCIPLES SEEKING INSTRUCTION AT THE LAKE PAVILION By Copyright 2016 Janet C. Chen Submitted to the graduate degree program in Art History and the Graduate Faculty of the University of Kansas in partial fulfillment of the requirements for the degree of Doctor of Philosophy. ________________________________ Chairperson Marsha Haufler ________________________________ Amy McNair ________________________________ Sherry Fowler ________________________________ Jungsil Jenny Lee ________________________________ Keith McMahon Date Defended: May 13, 2016 The Dissertation Committee for Janet C. Chen certifies that this is the approved version of the following dissertation: REPRESENTING TALENTED WOMEN IN EIGHTEENTH-CENTURY CHINESE PAINTING: THIRTEEN FEMALE DISCIPLES SEEKING INSTRUCTION AT THE LAKE PAVILION ________________________________ Chairperson Marsha Haufler Date approved: May 13, 2016 ii Abstract As the first comprehensive art-historical study of the Qing poet Yuan Mei (1716–97) and the female intellectuals in his circle, this dissertation examines the depictions of these women in an eighteenth-century handscroll, Thirteen Female Disciples Seeking Instructions at the Lake Pavilion, related paintings, and the accompanying inscriptions. Created when an increasing number of women turned to the scholarly arts, in particular painting and poetry, these paintings documented the more receptive attitude of literati toward talented women and their support in the social and artistic lives of female intellectuals. These pictures show the women cultivating themselves through literati activities and poetic meditation in nature or gardens, common tropes in portraits of male scholars. The predominantly male patrons, painters, and colophon authors all took part in the formation of the women’s public identities as poets and artists; the first two determined the visual representations, and the third, through writings, confirmed and elaborated on the designated identities.
    [Show full text]
  • Oral History and Genealogy of the Yuan Shikai Family
    City University of New York (CUNY) CUNY Academic Works Publications and Research Baruch College 2014 Research and Documentation in the 21st Century: Oral History and Genealogy of the Yuan Shikai Family Sheau-yueh J. Chao CUNY Bernard M Baruch College How does access to this work benefit ou?y Let us know! More information about this work at: https://academicworks.cuny.edu/bb_pubs/11 Discover additional works at: https://academicworks.cuny.edu This work is made publicly available by the City University of New York (CUNY). Contact: [email protected] ISSN 1712-8358[Print] Cross-Cultural Communication ISSN 1923-6700[Online] Vol. 10, No. 4, 2014, pp. 5-17 www.cscanada.net DOI:10.3968/4870 www.cscanada.org Research and Documentation in the 21st Century: Oral History and Genealogy of the Yuan Shikai Family Sheau-yueh J. Chao[a],* [a]Professor and Librarian, Head, Cataloging,William and Anita Newman and social and political studies. The paper ends with Library, Baruch College, City University of New York, New York, USA. the library documentation, preservation, and research in *Corresponding author. the 21st century focusing on the importance of Chinese Surported by two grants from the Research Foundation of the City family history and genealogical research for jiapu 家谱. University of New York, the PSC-CUNY Grants in 2008 and 2012. A selected bibliography about the Yuan Shikai family is included at the end for further readings. Received 23 February 2014; accepted 29 May 2014 Published online 25 June 2014 Highlights ● History of Chinese Names and Genealogical Abstract Records The oral histories and genealogies have long been used ● Types of Chinese Names and their Meanings by historians, archaeologists, sociologists, ethnologists, ● Oral History and Genealogy of the Yuan Shikai and demographers in their investigation of past human Family behavior on social and historical evidences relating to ● Resource and Documentation on Chinese a lineage organization or a clan.
    [Show full text]