A Bayesian Implementation of the Multispecies Coalescent Model with Introgression for Comparative Genomic Analysis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

1 Respiratory Motion Tracking in Magnetic Resonance Imaging With
Respiratory Motion Tracking in Magnetic Resonance Imaging with Pilot Tone Technology Thesis Presented in Partial Fulfillment of the Requirements for the Degree Master of Science in the Graduate School of The Ohio State University By Mary Lenk Graduate Program in Electrical and Computer Engineering The Ohio State University 2018 Thesis Committee Dr. Lee Potter, Advisor Dr. Rizwan Ahmad 1 Copyrighted by Mary Lenk 2018 2 Abstract This thesis explores the hypothesis that Pilot Tone (PT) technology can encode respiratory induced motion of the heart to improve cardiac magnetic resonance (MR) imaging. Pilot tone technology is advantageous due to its high sampling rate to provide high temporal resolution in tracking and predicting respiration. Also, the PT signal has the potential to provide motion information without interrupting the pulse sequence to perform motion compensated scans. A prediction model is hypothesized to account for in-plane and through-plane motions due to respiration. A proof-of-concept experiment was designed to explore the ability of the PT signal to encode respiratory-induced motion. The PT signal was processed retrospectively offline and compared to a reference for respiratory motion. The two signals had a high correlation and show preliminary success for the PT to detect respiration. A linear filter was then designed to predict motion from a training phase using the same reference signal. The linear filter was successful with peak/trough locations between the prediction and the reference signal having a correlation coefficient of 0.9999 for end-expiration and end-inspiration prediction. Furthermore, a PT transmitter was designed and constructed for implementation of additional experiments. -

Pilot Stories
PILOT STORIES DEDICATED to the Memory Of those from the GREATEST GENERATION December 16, 2014 R.I.P. Norm Deans 1921–2008 Frank Hearne 1924-2013 Ken Morrissey 1923-2014 Dick Herman 1923-2014 "Oh, I have slipped the surly bonds of earth, And danced the skies on Wings of Gold; I've climbed and joined the tumbling mirth of sun-split clouds - and done a hundred things You have not dreamed of - wheeled and soared and swung high in the sunlit silence. Hovering there I've chased the shouting wind along and flung my eager craft through footless halls of air. "Up, up the long delirious burning blue I've topped the wind-swept heights with easy grace, where never lark, or even eagle, flew; and, while with silent, lifting mind I've trod the high untrespassed sanctity of space, put out my hand and touched the face of God." NOTE: Portions Of This Poem Appear On The Headstones Of Many Interred In Arlington National Cemetery. TABLE OF CONTENTS 1 – Dick Herman Bermuda Triangle 4 Worst Nightmare 5 2 – Frank Hearne Coming Home 6 3 – Lee Almquist Going the Wrong Way 7 4 – Mike Arrowsmith Humanitarian Aid Near the Grand Canyon 8 5 – Dale Berven Reason for Becoming a Pilot 11 Dilbert Dunker 12 Pride of a Pilot 12 Moral Question? 13 Letter Sent Home 13 Sense of Humor 1 – 2 – 3 14 Sense of Humor 4 – 5 15 “Poopy Suit” 16 A War That Could Have Started… 17 Missions Over North Korea 18 Landing On the Wrong Carrier 19 How Casual Can One Person Be? 20 6 – Gardner Bride Total Revulsion, Fear, and Helplessness 21 7 – Allan Cartwright A Very Wet Landing 23 Alpha Strike -

Science Fiction Stories with Good Astronomy & Physics
Science Fiction Stories with Good Astronomy & Physics: A Topical Index Compiled by Andrew Fraknoi (U. of San Francisco, Fromm Institute) Version 7 (2019) © copyright 2019 by Andrew Fraknoi. All rights reserved. Permission to use for any non-profit educational purpose, such as distribution in a classroom, is hereby granted. For any other use, please contact the author. (e-mail: fraknoi {at} fhda {dot} edu) This is a selective list of some short stories and novels that use reasonably accurate science and can be used for teaching or reinforcing astronomy or physics concepts. The titles of short stories are given in quotation marks; only short stories that have been published in book form or are available free on the Web are included. While one book source is given for each short story, note that some of the stories can be found in other collections as well. (See the Internet Speculative Fiction Database, cited at the end, for an easy way to find all the places a particular story has been published.) The author welcomes suggestions for additions to this list, especially if your favorite story with good science is left out. Gregory Benford Octavia Butler Geoff Landis J. Craig Wheeler TOPICS COVERED: Anti-matter Light & Radiation Solar System Archaeoastronomy Mars Space Flight Asteroids Mercury Space Travel Astronomers Meteorites Star Clusters Black Holes Moon Stars Comets Neptune Sun Cosmology Neutrinos Supernovae Dark Matter Neutron Stars Telescopes Exoplanets Physics, Particle Thermodynamics Galaxies Pluto Time Galaxy, The Quantum Mechanics Uranus Gravitational Lenses Quasars Venus Impacts Relativity, Special Interstellar Matter Saturn (and its Moons) Story Collections Jupiter (and its Moons) Science (in general) Life Elsewhere SETI Useful Websites 1 Anti-matter Davies, Paul Fireball. -

The Drink Tank Sixth Annual Giant Sized [email protected]: James Bacon & Chris Garcia
The Drink Tank Sixth Annual Giant Sized Annual [email protected] Editors: James Bacon & Chris Garcia A Noise from the Wind Stephen Baxter had got me through the what he’ll be doing. I first heard of Stephen Baxter from Jay night. So, this is the least Giant Giant Sized Crasdan. It was a night like any other, sitting in I remember reading Ring that next Annual of The Drink Tank, but still, I love it! a room with a mostly naked former ballerina afternoon when I should have been at class. I Dedicated to Mr. Stephen Baxter. It won’t cover who was in the middle of what was probably finished it in less than 24 hours and it was such everything, but it’s a look at Baxter’s oevre and her fifth overdose in as many months. This was a blast. I wasn’t the big fan at that moment, the effect he’s had on his readers. I want to what we were dealing with on a daily basis back though I loved the novel. I had to reread it, thank Claire Brialey, M Crasdan, Jay Crasdan, then. SaBean had been at it again, and this time, and then grabbed a copy of Anti-Ice a couple Liam Proven, James Bacon, Rick and Elsa for it was up to me and Jay to clean up the mess. of days later. Perhaps difficult times made Ring everything! I had a blast with this one! Luckily, we were practiced by this point. Bottles into an excellent escape from the moment, and of water, damp washcloths, the 9 and the first something like a month later I got into it again, 1 dialed just in case things took a turn for the and then it hit. -

Anthology Electronic Letterhead
‘AINA PONO – HAWAII’S FARM TO SCHOOL PROGRAM JUNE 2018 Prepared for: The Office of the Lieutenant Governor of the State of Hawaii, through The Kohala Center BACKGROUND & METHODOLOGY The Office of the Lieutenant Governor of the State of Hawaii, through The Kohala Center, contracted Anthology Marketing Group’s research team to conduct research to better understand the agricultural landscape in Hawaii, as part of a broader effort to find opportunities to help the State of Hawaii’s Farm to School program, ‘Aina Pono, be successful. ‘Aina Pono is HIDOE’s pioneering farm to school pilot initiative that aims to bring more healthy, nutritious, fresh, and local food to school cafeterias throughout Hawaii. One of its key goals is to systematically increase HIDOE’s purchasing of local food for school breakfast, lunch, and snack programs, thereby increasing the penetration of local food (i.e., grown and/or raised within the State of Hawaii) to 40% from the current level of 23%. Research Objectives Better understand existing barriers for food distributors and farmers to respond to HIDOE solicitations for locally-grown produce, meat and other food. Solicit feedback on HIDOE solicitation document language, terms and solicitation process. Identify products currently available to distributors (or produced by local farmers) that could be incorporated into the DOE lunch program, and better understand production calendars of crops. Better understand barriers and incentives for farmers to work with distributors, HIDOE. To achieve the aforementioned objectives, Anthology Research conducted 22 in-depth interviews with various stakeholders in Hawaii agriculture. The interviews were conducted either in-person or over the phone between April 10 and June 22, 2018. -

Inference of Population History Using Coalescent Hmms: Review and Outlook
Inference of Population History using Coalescent HMMs: Review and Outlook Jeffrey P. Spencea, Matthias Steinr¨uckenb, Jonathan Terhorstc, and Yun S. Songd,e,* aComputational Biology Graduate Group, University of California, Berkeley bDepartment of Ecology and Evolution, University of Chicago cDepartment of Statistics, University of Michigan dComputer Science Division and Department of Statistics, University of California, Berkeley eChan Zuckerberg Biohub, San Francisco *To whom correspondence should be addressed: [email protected] Abstract Studying how diverse human populations are related is of historical and anthropological interest, in addition to providing a realistic null model for testing for signatures of natural selection or disease associ- ations. Furthermore, understanding the demographic histories of other species is playing an increasingly important role in conservation genetics. A number of statistical methods have been developed to infer population demographic histories using whole-genome sequence data, with recent advances focusing on allowing for more flexible modeling choices, scaling to larger data sets, and increasing statistical power. Here we review coalescent hidden Markov models, a powerful class of population genetic inference meth- ods that can effectively utilize linkage disequilibrium information. We highlight recent advances, give advice for practitioners, point out potential pitfalls, and present possible future research directions. 1 Introduction Using genetic data to understand the history of a population has been a long-standing goal of population genetics [1], and the emergence of massive data sets with individuals from many populations (e.g., [2{ 4]), often including ancient samples [5], have enabled the inference of increasingly realistic models of the genetic history of human populations, e.g., [6{8]. -

Matrix July / August 1997 £1.25
The News Magazine of the British Science Fiction Association Issue 126 matrix July / August 1997 £1.25 BSrA Surver Resulls, ,W~r Do You Bur 800~s1 ,,Movie News, ,Heary Melal ,,800~s, ,letters Chrls Terran ~ Editor 9 Beechwood Court allUIlCfedtedtext Back Beechwood Grove anworll,and Leeds, UK pOOtosraphy LS42HS [email protected] ~ Email emailwiabefcwwilOed klm\lweeldy John Ashbrook ~ Media ShepKirkbride ~ Artwork (page 11) lan Brooks ~ Logo Chrls Terran ~ Photography &Cover Chrls Terran ~ Design I Production Next Deadline BSFA~shipQ.. costs £\8 Iyaar1c' UK residlVrls, £17 $lancirlll order, £12l.t1waged,Lilemernbt<ship£180, Overseu:Europe £2:J.50,elsewhtre£23.50 surface mail,£30arma Cl\t1f.les payablt to BSFA lid All non-US mOOlbershipqJOOes. Q" PlulBllllnoger renewals,adti'esscNonges . .-- 0 I LoogAowCIose,Everdorl,Oaver1try, members Northanrs.NN1138E nts <l) 01327361661 US ~ : ~~ld~~:[email protected] All US subsaiplions. s 1~48W"lredSlr...,Oel,cNt.~1482\3,U,S_A. $3S$U~<lC&,S45a~, payable to CyCkauvin(BSFA) BSFA Aoniristralat Q" Maureen Klncakl Speller [!J 608oI¥nemoJthRoad,Fo/kfltone,KenI,CTl9SAl News -i the happening world Cl> 01303252939 +- 03 * IlksJ>kfcix.co,uk Recent And Forthcoming Books +- 07 -i words words words BSFA T,eawt< Q' Ellzlbeth Bllllnger o llon<;lRowCIose,EWlI'dorl,Davenrry. Books, &c +- 11 -i brlan ameringen and NorthanlS..NN113BE Catchin' the Collectin' Bug carollne mullan wonder Cl> 01321361661 why you bUy books * billingerlenterprise.net Mailbox +- 12 -i letters Omters Q' ~roIAnnK""YGteen TheBSFA'swntinggroups -
Reciprocal Haunting: Pat Barker's Regeneration Trilogy
Karen Patrick Knutsen Karen Patrick Reciprocal Haunting Faculty of Arts and Education English Reciprocal Haunting: Pat Barker's Reciprocal Pat Barker’s fictional account of the Great War, The Regeneration Trilogy, completed in 1995, won wide popular and critical acclaim and established her as a major contemporary British writer. Although the trilogy appears to be written in the realistic style of the traditional historical novel, Barker approaches the past with certain preoccupations from 1990s Britain and rewrites the past as seen through these contemporary lenses. Consequently, the trilogy conveys a sense of reciprocal haunting; the past Karen Patrick Knutsen returns to haunt the present, but the present also haunts Barker’s vision of the past. This haunting quality is developed through an extensive, intricate pattern of intertextuality. This study offers a reading of trauma, class, gender and psychology as thematic areas where intertexts Regeneration are activated, allowing Barker to revise and re-accentuate stories of the past. Drawing on Michel Foucault’s concept of discourse and Mikhail Bakhtin’s notion of dialogue, it focuses on the trilogy as an interactive link in an intertextual chain of communication about the Great War. My reading shows that the trilogy presents social structures from different historical epochs through dialogism and Trilogy Reciprocal Haunting diachronicity, making the present-day matrices of power and knowledge that continue to determine people’s lives highly visible. The Regeneration Trilogy regenerates the past, simultaneously confirming Barker’s claim that the historical novel can also be “a backdoor into the present”. Pat Barker's Regeneration Trilogy Karlstad University Studies DISSERTATION ISSN 1403-8099 Karlstad University Studies ISBN 978-91-7063-176-4 2008:17 Karen Patrick Knutsen Reciprocal Haunting Pat Barker's Regeneration Trilogy DISSERTATION Karlstad University Studies 2008:17 Karen Patrick Knutsen. -

Coalescent Genealogy Samplers: Windows Into Population History
Review Coalescent genealogy samplers: windows into population history Mary K. Kuhner Department of Genome Sciences, University of Washington, Box 355065, Seattle, WA 98195-5065, USA Coalescent genealogy samplers attempt to estimate growing populations, showing how the relative timing of past qualities of a population, such as its size, growth coalescences varies with growth rate. rate, patterns of gene flow or time of divergence from Coalescent genealogy samplers have been used to study another population, based on samples of molecular diverse populations of organisms, including HIV-1 isolates data. Genealogy samplers are increasingly popular from a clinical outbreak [9], rabbits in a European hybrid because of their potential to disentangle complex popu- zone [10], Beringian bison in the Pleistocene and Holocene lation histories. In the last decade they have been widely epochs [11] and Japanese conifers [12]. When used prop- applied to systems ranging from humans to viruses. erly, these samplers are powerful tools for gaining insight Findings include detection of unexpected reproductive into population histories. In this review, I will discuss the inequality in fish, new estimates of historical whale advantages of genealogy samplers over competing abundance, exoneration of humans for the prehistoric decline of bison and inference of a selective sweep on the human Y chromosome. This review summarizes avail- able genealogy-sampler software, including data Glossary requirements and limitations on the use of each pro- AIC: Akaike information criterion, a heuristic used to determine whether the gram. improvement in fit of a more complex model justifies the additional parameters it introduces. Introduction Bayesian skyline plot: a graph showing the curve of inferred population size The larger a population is, the more distantly, on average, over time (and its support intervals) based on multiple sampled genealogies. -

The Panama Canal Review Caccomplidhment
UNIVERSITY OF FLORIDA LIBRARIES Digitized by the Internet Archive in 2010 with funding from University of Florida, George A. Smathers Libraries http://www.archive.org/details/panamacanalrefeb1967pana .KY 1967 V7 H. R. Parfitt, Acting Governor Robert D. Kerr, Press Officer Publications Editors Frank A. Baldwin Morgan E. Goodwin and Tomas A. Cupas Panama Canal Information Officer Editorial Assistants Official Panama Canal Publication Eunice Richard, Tobi Bittel, Fannie P. Published quarterly at Balboa Heights, C.Z Hernandez, and Jose T. Tunon Printed at the Printing Plant, La Boca, C.Z. Review articles may be reprinted in full or part without further clearar ce. Credit to the Review will be appreciated. Distributed free of charge to all . Panama Canal Employees Subscriptions, $1 a year; airmail $2 a year; mail and back copies (regular mail), 25 cents each cAoout Our Ctover 3ndex THE FACE OF the man on the cover is familiar to Governor Fleming's Legacy 3 thousands of residents of the Isthmus. Bullfighting 5 Canal Zone Gov. Robert Fleming, has just closed J. Jr., Panama Canal Pilots q out his career as chief executive for the Panama Canal Canal History q organization after a 5-year stay, longer than that of any Battle of the Bugs iq predecessor. Before departing Panama to take a highly Ports of the World 12 responsible position in Florida, Governor Fleming also Skindiving rang 24 down the curtain on his outstanding military career. Shipping Statistics i§ Governor and Mrs. Fleming, both of whom were deco- Shipping Trends ig rated with Panama's Order of Vasco Nunez de Balboa, Anniversaries of) will be missed by their friends and acquaintances. -

Fantasyland/Aggieland
FANTASYLAND/AGGIELAND: A Bibliographic History of Science Fiction and Fantasy at Texas A&M University and in Brazos County, Texas, 1913-1985. compiled by Bill Page College Station, TX 2007 Page 1 of 134 INTRODUCTION Bill Page None of the local activites before 1967 were part of any fannish organizations -- at least not as far as I can determine. There's really no way to pick an exact beginning date for the history of science fiction and fantasy in Brazos County. For example, Bryan had a book store by 1870. It probably sold an occasional fantasy or science fiction novel, such as The Tempest or Frankenstein. After the end of the Civil War, newspapers, including the Galveston News, could be purchased in the county, as were magazines such as Godey's Ladies Book and Leslies Illustrated Weekly. These carried an occasional sf/f story. Persons wanting to know more about the early history of newspapers, magazines, libraries, and literary societies in Brazos County should read the chapters "Libraries," "Lodges and Civic Organizations," and "Cultural History: The Arts and Recreation in the Nineteenth Century" in Brazos County History: Rich Past -- Bright Future. I'm not sure when the first fantasy or science fiction film was shown in the county. Movies came to Bryan at least as early as January 1897, when "the magniscope, Edison's latest and greatest invention in the way of vitascopes" appeared in the Grand Opera House. (See the Bryan Daily Eagle, January 28, 1897, p. 4, cols. 2, 6). Page 2 of 134 Additional Sources: Additional material on the fantastic at Texas A&M University after 1985 can be found in several sources. -
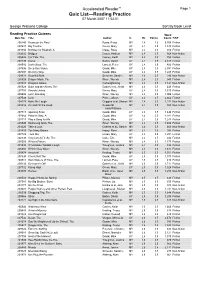
Accelerated Reader™ Page 1 Quiz List—Reading Practice 07 March 2007 11:52:51
Accelerated Reader™ Page 1 Quiz List—Reading Practice 07 March 2007 11:52:51 George Watsons College Sort By Book Level Reading Practice Quizzes Word Quiz No. Title Author IL BL Points Count F/NF 200240 Beans on the Roof Byars, Betsy MY 2.4 1.0 5,768 Fiction 207687 Big Trouble Green, Mary UY 2.4 0.5 1,340 Fiction 201834 Birthday for Bluebell, A Impey, Rose MY 2.4 0.5 916 Fiction 203202 Bridges Casey, Andrew MY 2.4 0.5 868 Non-fiction 205526 Car Talk, The Gaines, Keith MY 2.4 0.5 755 Fiction 207499 Coma Belbin, David UY 2.4 0.5 2,617 Fiction 208510 Dark Glass, The Lancett, Peter UY 2.4 0.5 400 Fiction 207696 Deep Sea Vision Gould, Mike UY 2.4 0.5 2,591 Fiction 207697 Do it my Way Gould, Mike UY 2.4 0.5 1,285 Fiction 209323 Downhill BMX Schuette, Sarah L. MY 2.4 0.5 290 Non-fiction 205528 Dragon Mask, The Wren, Wendy MY 2.4 0.5 945 Fiction 203003 Dragons Galore Cartwright/Ling MY 2.4 0.5 1,141 Non-fiction 205529 Duke and the Aliens, The Gaines et al., Keith MY 2.4 0.5 449 Fiction 207703 Friends United Green, Mary UY 2.4 0.5 1,310 Fiction 205506 Lost! One Bag Wren, Wendy MY 2.4 0.5 1,006 Fiction 207508 Luck Prince, Alison UY 2.4 0.5 2,662 Fiction 204174 Make Me Laugh Griggins et al, Sharon MY 2.4 0.5 1,232 Non-fiction 203216 On and Off the Road Reeder/St MY 2.4 0.5 800 Non-fiction John/Williams 207713 Opening Soon Gould, Mike UY 2.4 0.5 1,444 Fiction 207684 Place to Stay, A Gould, Mike UY 2.4 0.5 1,281 Fiction 207717 Play a Song for Me Gould, Mike UY 2.4 0.5 1,243 Fiction 205540 Swimming Gala, The Wren, Wendy MY 2.4 0.5 1,404 Fiction 203220