DOCSLIB.ORG

Self-Stabilizing Wormhole Routing

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Self-Stabilizing Wormhole Routing UNLV Retrospective Theses & Dissertations 1-1-2002 Self-stabilizing wormhole routing Anthony Brandon Kenitzki University of Nevada, Las Vegas Follow this and additional works at: https://digitalscholarship.unlv.edu/rtds Repository Citation Kenitzki, Anthony Brandon, "Self-stabilizing wormhole routing" (2002). UNLV Retrospective Theses & Dissertations. 1415. http://dx.doi.org/10.25669/j56d-d0pm This Thesis is protected by copyright and/or related rights. It has been brought to you by Digital Scholarship@UNLV with permission from the rights-holder(s). You are free to use this Thesis in any way that is permitted by the copyright and related rights legislation that applies to your use. For other uses you need to obtain permission from the rights-holder(s) directly, unless additional rights are indicated by a Creative Commons license in the record and/ or on the work itself. This Thesis has been accepted for inclusion in UNLV Retrospective Theses & Dissertations by an authorized administrator of Digital Scholarship@UNLV. For more information, please contact [email protected]. INFORMATION TO USERS This manuscript has been reproduced from the microfilm master. UMI films the text directly from the original or copy submitted. Thus, some thesis and dissertation copies are in typewriter face, while others may be from any type of computer printer. The quality of this reproduction is dependent upon the quality of the copy submitted. Broken or indistinct print, colored or poor quality illustrations and photographs, print bleedthrough, substandard margins, and improper alignment can adversely affect reproduction. In the unlikely event that the author did not send UMI a complete manuscript and there are missing pages, these will be noted. Also, if unauthorized copyright material had to be removed, a note will indicate the deletion. Oversize materials (e.g., maps, drawings, charts) are reproduced by sectioning the original, beginning at the upper left-hand comer and continuing from left to right in equal sections with small overlaps. ProQuest Information and Learning 300 North Zeeb Road, Ann Arbor, Mi 48106-1346 USA 800-521-0600 UMI' Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. SELF-STABinZING WORMHOLE ROUTING bv Anthonv B. Kenitzki Bachelor of Arts College of Engineering University of Nevada. Las Vegas 1997 A thesis submitted in partial fulfillment of the requirements for the M aster of Science Degree Department of Computer Science Howard R. Hughes College of Engineering Graduate College University of Nevada. Las Vegas August 2002 Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. UMI Number 1411274 UMI‘ UMI Microform 1411274 Copyright 2003 by ProQuest information and Learning Company. All rights reserved. This microform edition is protected against unauthoriæd copying under Title 17, United States Code. ProQuest Information and Learning Company 300 North Zeeb Road P.O. Box 1346 Ann Arbor, Ml 48106-1346 Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. Thesis Approval IJNTV The Graduate College University of Nevada, Las Vegas May 17 20 02 The Thesis prepared by Anthony B Kenitzki Entitled Self-Stabilizing Wormhole Routing is approved in partial fulfillment of the requirements for the degree of Master of Science in Computer Science __________________ Examination Committee Qtair Examination Committee Chair van o f the Graduate College Examination Committee Member Examination Comjmttèe Member Graduate clllege Facidty Representative u Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. ABSTRACT Self Stabilizing Wormhole Routing by Anthony B. Kenitzki Ajoy K. Datta PhD. Examination Committee Co-Chair Professor of Computer Science University of Nevada. Las Vegas Sébastien Tixeuil PhD. Examination Committe Co-Chair Professor of Computer Science Université de Paris-Sud. France Parallel and distributed systems are composed of individual processors that communicate with one another by exchanging messages through communication links. WTien the sender and the re­ ceiver of a message are not direct neighbors, intermediate processors must cooperate to ensure proper routing. Wormhole routing is most common in parallel architectures in which messages are sent in small fragments called flits. We assume that each processor will contain a single fixed-size flit buffer for each incoming link. A processor must forward the flit in a given link buffer to another processor before receiving another flit on that link. This permits messages to wind through the entire network from source to destination, resembling a worm. Wormhole routing is a lightweight and efficient method of routing messages between parallel processors. Oiur purpose is to modify existing wormhole routing algorithms in familiar topologies to make iii Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. them self-stabilizing. Self-stabilization is a technique that guarantees tolerance to transient faults (e.g. memory corruption or communication hazard) for a given protocol. Transient faults would t\-p- ically place the network in an illegitimate state, while Self-stabilization guarantees that the network recovers a correct behavior in finite time, without the need for human intervention. Self-stabilization also guarantees the safety property, meaning that once the network is in a legitimate state, it will remain there until another fault occurs. This paper presents self-stabilizing network algorithms in the wormhole routing model, using the unidirectional ring and the two-dimensional mesh topologies. We chose the ring topology to illustrate the numerous difficulties of self-stabilization in a wormhole routing environment, even in one of the most simple network topologies. We then extend the results of the ring topology to a more complex two-dimensional mesh network. IV Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. TABLE OF CONTENTS ABSTRACT ........................................................................................................................................ iii LIST OF FIGURES ........................................................................................................................... \ii LIST OF ALGORITHMS................................................................................................................. viii ACKNOWLEDGMENTS................................................................................................................. ix CHAPTER I INTRODUCTION ................................................................................................. I Processor Networks........................................................................................................................ I Topology........................................................................................................................................... 1 Self-stabilization ........................................................................................................................... 2 Routing Protocols ........................................................................................................................ 2 Related W ork ................................................................................................................................. 3 Our Contribution ........................................................................................................................... 3 Thesis Outline .............................................................................................................................. 4 CHAPTER 2 SELF-STABILIZING WORMHOLE ROUTING IN R IN G S ....................... 5 Network Model and Topology .................................................................................................... 5 Wormhole Routing ....................................................................................................................... 5 Specification .................................................................................................................................... 6 Problems Encountered ................................................................................................................. 6 Solutions and Ideas ....................................................................................................................... 7 Assumptions and Conventions .................................................................................................... 8 Programming Conventions .......................................................................................................... 10 Data Structures .............................................................................................................................. 10 A lgorithm........................................................................................................................................ 12 Helper Functions .................................................................................................................... 12 Algorithm Description............... 13 Proof of C o rre c tn e ss ...................................................................................................................
Load more

Recommended publications
  • View Document
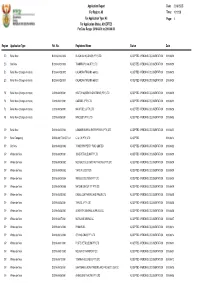
    Application Report Date: 2016/05/05 For Region: All Time: 10:19:28 For Application Type: All Page: 1 For Application Status: ACCEPTED For Date Range: 2016/04/01 to 2016/04/30 Region Application Type Ref. No. Registered Name Status Date EC Retail New B/2016/04/20/0002 BLACK OIL HOLDINGS (PTY) LTD ACCEPTED - PENDING DOCUMENTATION 2016/04/20 EC Site New B/2016/04/20/0001 TRAKPROPS 146 (PTY) LTD ACCEPTED - PENDING DOCUMENTATION 2016/04/20 EC Retail New (Change-of-Hands) B/2016/04/25/0002 CALANDRA TRADING 669 CC ACCEPTED - PENDING DOCUMENTATION 2016/04/25 EC Retail New (Change-of-Hands) B/2016/04/25/0001 CALANDRA TRADING 669 CC ACCEPTED - PENDING DOCUMENTATION 2016/04/25 FS Retail New (Change-of-Hands) C/2016/04/29/0001 HECTOR AUSTIN ENGINEERING (PTY) LTD ACCEPTED - PENDING DOCUMENTATION 2016/04/29 FS Retail New (Change-of-Hands) C/2016/04/21/0001 DAIZEBEL (PTY) LTD ACCEPTED - PENDING DOCUMENTATION 2016/04/21 FS Retail New (Change-of-Hands) C/2016/04/26/0001 MAJA FUELS (PTY) LTD ACCEPTED - PENDING DOCUMENTATION 2016/04/26 FS Retail New (Change-of-Hands) C/2016/04/08/0001 MINOZEST (PTY) LTD ACCEPTED - PENDING DOCUMENTATION 2016/04/08 GP Retail New D/2016/04/22/0003 LAMANI BUSINESS ENTERPRISES (PTY) LTD ACCEPTED - PENDING DOCUMENTATION 2016/04/22 GP Retail Temporary D/2006/08/17/0015/T16/1 CJ & CK (PTY) LTD ACCEPTED 2016/04/14 GP Site New D/2016/04/22/0002 TOWER PROPERTY FUND LIMITED ACCEPTED - PENDING DOCUMENTATION 2016/04/22 GP Wholesale New D/2016/04/29/0001 JUNE PETROLEUM PTY LTD ACCEPTED - PENDING DOCUMENTATION 2016/04/29 GP Wholesale New
    [Show full text]
  • AMD Geode™ LX Processors Data Book
    AMD Geode™ LX Processors Data Book February 2007 Publication ID: 33234E AMD Geode™ LX Processors Data Book © 2007 Advanced Micro Devices, Inc. All rights reserved. The contents of this document are provided in connection with Advanced Micro Devices, Inc. (“AMD”) products. AMD makes no representations or warranties with respect to the accuracy or completeness of the contents of this publication and reserves the right to make changes to specifications and product descriptions at any time without notice. No license, whether express, implied, arising by estoppel or otherwise, to any intellectual property rights is granted by this publication. Except as set forth in AMD’s Standard Terms and Conditions of Sale, AMD assumes no liability whatsoever, and disclaims any express or implied warranty, relating to its products including, but not limited to, the implied warranty of mer- chantability, fitness for a particular purpose, or infringement of any intellectual property right. AMD’s products are not designed, intended, authorized or warranted for use as components in systems intended for surgical implant into the body, or in other applications intended to support or sustain life, or in any other application in which the failure of AMD’s product could create a situation where personal injury, death, or severe property or environmental damage may occur. AMD reserves the right to discontinue or make changes to its products at any time without notice. Contacts www.amd.com Trademarks AMD, the AMD Arrow logo, AMD Athlon, AMD Geode, and combinations thereof, and 3DNow! and GeodeLink, are trademarks of Advanced Micro Devices, Inc. AMD-K6 is a registered trademark of Advanced Micro Devices, Inc.
    [Show full text]
  • System/370 Model 145 Reference Summary
    System/370 Model 145 Reference Summary S229-2239-1 IBM Corporation, Field Support Documentation, Dept 927, Rochester, Minnesota 55901 PREFACE This publication is primarily intended for customer engineers servicing System/370 Model 145. Second Edition (September 1972) This is a major revision of, and makes 8229-2239-0 obsolete. Address any comments concerning the contents of this publication to: IBM, Field Support Documentation, Dept 927, Rochester, Minnesota 55901 © International Business Machines Corporation 1972 CONTENTS Section 1 - Control Words Branch and Module Switch Word "O" . 1. 1 Branch Word . 1.2 GA Function Charts . 1.3 GA Function Charts . 1.4 GA Function Charts . 1.5 Branch and Link or Return Word . 1.6 Word Move Word Version"O" . 1. 7 Word Move Word Version "1" . 1.8 Storage Word, Non K-Addressable . 1.9 Storage Word, K-Addressable . 1.10 Arithmetic Word 10 Byte Version 1.11 Arithmetic Word, Fullword Version 1.12 Arithmetic Word, 11 Direct ByteVersion . 1.13 Arithmetic Word, 10/11 Indirect Byte Version . 1.14 ALU Entry Gating 1.15 Stat Set Symbols . 1.15 BranchSymbols . 1.15 Arithmetic Word Chart Selection 1.16 Address Formation Chart 1.16 Control Word Chart Selection 1.16 Section 2 - CPU 3145 CPU Data Flow . 2.1 I-Cycles Data Flow . 2.2 I-Cycles . 2.3 PSW Locations . 2.3 Expanded Local Storage . 2.3 I-Cycles . 2.3 I-Cycles Control Line Generation . 2.4 Control Word . 2.4 Control Register Decode . 2.4 iii ECCL Board Layout ............ 2.5 Data Bit Location Chart .......... 2.5 Common Test Points ...........
    [Show full text]
  • Prioritization 4.0
    Prioritization 4.0 NCDOT Strategic Prioritization Office of Transportation July 2015 Agenda • Background • General Overview of Changes From P3.0 To P4.0 • Scoring and Scaling • Peak ADT • In-Depth Review of P4.0 Highway Criteria, Measures and Weights • In-Depth Review of P4.0 Non-Highway Criteria, Measures and Weights • Timeline/Schedule • SPOT On!ine • Local Input Methodologies and Best Practices 2 Background NCDOT is responsible for 6 modes of transportation: • Aviation (74 publicly‐owned airports) • Bicycle and Pedestrian • Ferries –2nd largest system in US (behind Washington) • Highways – Maintains 80,000 miles of highways (2nd only to Texas) • Public Transportation • Rail Annual Budget of approx. $4.1 B (federal dollars account for 25% of total budget) 3 Background Key Partners, as shown on colorful map below, include: • 19 Metropolitan Planning Organizations (MPOs) • 18 Rural Planning Organizations (RPOs) • 14 Field Offices (Divisions) *Unifour RPO has dissolved into adjacent MPOs 4 Strategic Transportation Investment (STI) New funding formula for NCDOT’s Capital Expenditures • Focus on Mobility/Expansion and Modernization projects for all modes House Bill 817 signed into Law June 26, 2013 Most significant transportation legislation in NC since 1989 Prioritization Workgroup charged with providing recommendations to NCDOT on weights and criteria. Reps include: • MPOs • RPOs • Division Engineers • Local Government Advocacy Groups 5 STI Legislation New funding formula for all capital expenditures, regardless of mode. All modes must
    [Show full text]
  • ILK]: Driver Should Make Sure the First 3D Command After the Engine Switch from BLT Not to Be 1
    Intel® OpenSource HD Graphics PRM Volume 1 Part 5: Graphics Core - Blitter Engine For the all new 2010 Intel Core Processor Family Programmer’s Reference Manual (PRM) March 2010 Revision 1.0 Doc Ref #: IHD_OS_V1Pt5_3_10 Creative Commons License You are free: to Share — to copy, distribute, display, and perform the work Under the following conditions: Attribution. You must attribute the work in the manner specified by the author or licensor (but not in any way that suggests that they endorse you or your use of the work). No Derivative Works. You may not alter, transform, or build upon this work. INFORMATION IN THIS DOCUMENT IS PROVIDED IN CONNECTION WITH INTEL® PRODUCTS. NO LICENSE, EXPRESS OR IMPLIED, BY ESTOPPEL OR OTHERWISE, TO ANY INTELLECTUAL PROPERTY RIGHTS IS GRANTED BY THIS DOCUMENT. EXCEPT AS PROVIDED IN INTEL’S TERMS AND CONDITIONS OF SALE FOR SUCH PRODUCTS, INTEL ASSUMES NO LIABILITY WHATSOEVER, AND INTEL DISCLAIMS ANY EXPRESS OR IMPLIED WARRANTY, RELATING TO SALE AND/OR USE OF INTEL PRODUCTS INCLUDING LIABILITY OR WARRANTIES RELATING TO FITNESS FOR A PARTICULAR PURPOSE, MERCHANTABILITY, OR INFRINGEMENT OF ANY PATENT, COPYRIGHT OR OTHER INTELLECTUAL PROPERTY RIGHT. Intel products are not intended for use in medical, life saving, or life sustaining applications. Intel may make changes to specifications and product descriptions at any time, without notice. Designers must not rely on the absence or characteristics of any features or instructions marked "reserved" or "undefined." Intel reserves these for future definition and shall have no responsibility whatsoever for conflicts or incompatibilities arising from future changes to them. The Sandy Bridge chipset family, Havendale/Auburndale chipset family, Intel® 965 Express Chipset Family, Intel® G35 Express Chipset, and Intel® 965GMx Chipset Mobile Family Graphics Controller may contain design defects or errors known as errata which may cause the product to deviate from published specifications.
    [Show full text]
  • Template Jurnal JAIC;
    Journal of Applied Informatics and Computing (JAIC) Vol.2, No.1, Juli 2018, pp. 7~10 e-ISSN: 2548-6861 7 Simulation Strategic Positioning for Mobile Robot Roccer Wheels Mochamad Mobed Bachtiar1, Iwan Kurnianto Wibowo2, Rakhmat Faizal Ajie3 Teknik Komputer, Politeknik Elektronika Negeri Surabaya [email protected] 1, [email protected] 2, [email protected] 3 Article Info ABSTRACT Article history: Soccer robot is a combination of sports, robotics technology and multi agent system. The achieve goals in playing the ball, requires individual intelligence, and the ability Received 2018-04-30 of cooperation for individual skills. The success of a soccer robot team is influenced Revised 2018-06-01 by the success of the robot player to enter the ball into the opponent's goal. In Accepted 2018-07-01 entering the ball into the opponent's goal needed an appropriate position and strategic. This research makes the design in finding a strategic position at the time Keyword: of attack. The design divides the field into several small areas or the main grid, strategic position; attack where each region gives different action. The position is said to be strategic if the strategy; empty space; naïve robot passing success and has a fairly wide perspective against the goal. The bayes classifier strategic position is gained from the greatest opportunity of some of the decisive conditions. The calculation used is to use the Probability Naïve Bayes Classifier by taking the maximum value that serve as a strategic position. So this research resulted in a design in finding strategic position. Copyright © 2017 Journal of Applied Informatics and Computing.
    [Show full text]
  • The New Tourism Lexicon: Rewriting Our Industry's Narrative
    POLICY BRIEF THE NEW TOURISM LEXICON: REWRITING OUR INDUSTRY'S NARRATIVE Last year, Destinations International released a policy "Washington is the problem. Remind voters again and brief entitled, “Advocacy in the Face of Ideology,” which again about Washington spending, Washington waste, made the case that relying on ROI numbers to defend Washington taxation, Washington bureaucracy, the value and relevancy of a destination organization Washington rules and Washington regulations." was no longer a viable advocacy strategy. Instead, we Luntz also suggested replacing "drilling for oil" with argued, destination organizations need to support the "exploring for energy," "undocumented workers" with message of ROI in terms of dollars and cents with an "illegal aliens," and "estate tax" with "death tax." The ideological and value-based appeal to convince political substitutions often work — an Ipsos/NPR poll found that leaders that without a destination organization, these support for abolishing the estate tax jumps to 76% from returns will inevitably vanish. 65% when you call it the death tax. Our industry has unfortunately fallen for what George Lakoff, a professor of Cognitive Science and Linguistics at the University of California at Berkeley, dubs the “Enlightenment Fallacy.” According to this viewpoint, you simply need to tell people the facts in clear language and they’ll reason to the right, true conclusions. The problem, as Lakoff puts it is, “The cognitive and brain sciences have shown this is false… it’s false in every single detail.” The reality is that people tend to frame political arguments, and the facts behind them, in terms of their own values.
    [Show full text]
  • Advanced Ipv6 Security in the LAN Gilles Roy, Technical Leader BRKSEC-3003 in 2015, 55% of Attacks Are from the Inside! *
    Advanced IPv6 Security in the LAN Gilles Roy, Technical Leader BRKSEC-3003 In 2015, 55% of attacks are from the inside! * Source: 2015 IBM Cyber Security Report 3 There is a lot happening on the LAN, it can be difficult to follow everything, lets break it down. 1. Operations 2. Attacks 3. Mitigations 4. Use cases 4 Use cases Enterprise SP Access Datacenter Address Allocation ✔ ✖ ✖ Duplicate Address Detection ✔ ✔ ✔ Address Resolution ✔ ✖ ✔ Operation Neighbor Unreachability Detection ✔ ✖ ✔ Prefix Allocation ✖ ✔ ✖ Making Default Router Discovery ✔ ✖ ✔ sense of Denial of Link Operations ✔ ✖ ✔ Denial of Address Resolution ✔ ✖ ✔ YOUR Router Theft ✔ ✔ ✔ Attacks Address Theft ✔ ✖ ✔ setup. Denial of Address Configuration ✔ ✔ ✖ Denial of Address Assignment ✔ ✖ ✖ RA Guard ✔ ✔ ✔ DHCP Guard ✔ ✔ ✖ Mitigation Source Guard ✔ ✖ ✔ Destination Guard ✔ ✖ ✖ Binding Guard ✔ ✖ ✔ 5 Abstract summary and pre-requisite • This session focuses on IPv6 security within the layer-2 domain • With a multi-dimensional approach: operations, vulnerabilities, mitigations and use-cases • It introduces security features at the First Hop, such RA Guard, Source Guard, Destination guard, etc • Requirements: Knowledge of IPv6 and IPv6 Neighbor Discovery 6 Agenda • IPv6 in the layer-2 domain: operations and protocols • IPv6 in the layer-2 domain: vulnerabilities • Attack Demonstration • Mitigating Vulnerabilities • Use cases overview 7 Some background on layer-2 & IPv6 • Layer-2: what is it? • Layer-2 domain: also “broadcast domain”, link, lan, vlan, segment • Nodes: hosts, routers,
    [Show full text]
  • Report on the Most Appropriate Indicators Related to the Basic Concepts
    D 4.1 – Report on the most appropriate indicators related to the basic concepts Report on the most appropriate indicators related to the basic concepts Deliverable D4.1 This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 870708 D 4.1 – Report on the most appropriate indicators related to the basic concepts Disclaimer: The contents of this deliverable are the sole responsibility of one or more Parties of the SmartCulTour consortium and can under no circumstances be regarded as reflecting the position of the Research Executive Agency and European Commission under the European Union’s Horizon 2020 programme. Copyright and Reprint Permissions “You may freely reproduce all or part of this paper for non-commercial purposes, provided that the following conditions are fulfilled: (i) to cite the authors, as the copyright owners (ii) to cite the SmartCulTour Project and mention that the EC co-finances it, by means of including this statement “Smart Cultural Tourism as a Driver of Sustainable Development of European Regions - SmartCulTour Project no. H2020-870708 co financed by EC H2020 program” and (iii) not to alter the information.” _______________________________________________________________________________________ How to quote this document: Petrić, L., Mandić, A., Pivčević, S., Škrabić Perić, B., Hell, M., Šimundić, B., Muštra, V., Mikulić, D., & Grgić, J. (2020). Report on the most appropriate indicators related to the basic concepts. Deliverable 4.1 of the Horizon 2020 project SmartCulTour (GA number 870708), published on the project web site on September 2020: http://www.smartcultour.eu/deliverables/ D 4.1 – Report on the most appropriate indicators related to the basic concepts This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No.
    [Show full text]
  • Nv9602 Nv9000 Control Panel
    NV9602 NV9000 CONTROL PANEL User’s Guide VERSION 1.2 UG0040-02 2015-07-02 www.grassvalley.com Notices Copyright and Trademark Notice Copyright © 2015, Grass Valley USA, LLC. All rights reserved. Belden, Belden Sending All The Right Signals, and the Belden logo are trademarks or registered trademarks of Belden Inc. or its affiliated companies in the United States and other jurisdictions. Grass Valley USA, LLC, Miranda, NV9602, Kaleido, NVISION, iControl, and Densité are trademarks or registered trademarks of Grass Valley USA, LLC. Belden Inc., Grass Valley USA, LLC, and other parties may also have trademark rights in other terms used herein. Terms and Conditions Please read the following terms and conditions carefully. By using NVISION control panel documentation, you agree to the following terms and conditions. Grass Valley hereby grants permission and license to owners of NVISION control panels to use their product manuals for their own internal business use. Manuals for Grass Valley products may not be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying and recording, for any purpose unless specifically authorized in writing by Grass Valley. A Grass Valley manual may have been revised to reflect changes made to the product during its manufacturing life. Thus, different versions of a manual may exist for any given product. Care should be taken to ensure that one obtains the proper manual version for a specific product serial number. Information in this document is subject to change without notice and does not represent a commitment on the part of Grass Valley. Warranty information is available in the Support section of the Grass Valley Web site (www.grassvalley.com).
    [Show full text]
  • The (Many) Paths to “Destination X”
    Blog The (many) paths to “Destination X” Michelle Batten Head of Global Marketing, Mobile Division, Amadeus According to Amadeus’ new whitepaper, Better travel in the Live Travel Space “Get ready for Destination X,” today’s travel sellers have a golden opportunity to Destination X also offers enormous tap into destination services, a growing untapped potential to market and sell marketplace set to reach $183 billion by ancillary destination services to travelers. 2020. Drawing on survey results from It’s a place where travel agents, corporate more than a thousand CheckMyTrip by travel programs, and other providers of Amadeus mobile app users, the research flights, hotels and cars can continue identifies emerging trends about business servicing travelers at their final destination. and leisure travelers destined for Whether traveling on business, leisure or Destination X, one of the most important bleisure, mobile provides the perfect revenue-generating stops on a traveler’s platform to offer these destination services journey. on the move. Take me to travel nirvana Amadeus is helping travel providers better understand and address these challenges The Amadeus research poses questions and opportunities. Using the Amadeus such as, “Are travelers prepared as they Travel Platform, the Live Travel Space arrive to Destination X?” Are their needs aggregates all content into one platform, for add-on destination services like airport making it easier for travel sellers to find transfers, local activities and restaurant what they need, and provide the level of reservations being met? The paper personalization their travelers demand. explores eight trends regarding the challenges and opportunities travel sellers Are you ready to service customers more face in the post-booking ancillary game fully when they reach Destination X? and how you can win travelers trust in Download the whitepaper today at that arena.
    [Show full text]
  • Assessing Contamination Risks Associated with Dust Soil Composted
    Assessing Contamination Risk of Dust, Soil, Compost, Compost Amended Soil and Irrigation Water as Vehicles of Pathogen Contamination on Iceberg Lettuce Surfaces Sadhana Ravishankar and Govindaraj Dev Kumar School of Animal & Comparative Biomedical Sciences, University of Arizona, Tucson, AZ 85721 Project Report Submitted to the Arizona Iceberg Lettuce Research Council, 2014 1 Introduction The contamination of fresh produce by foodborne pathogens results in 9.5 million illnesses in the United States annually, causing $39 billion in medical losses (Schraff 2010). Iceberg lettuce and similar leafy greens are usually consumed raw with minimal processing or heat treatment. Hence, there is an increased risk of pathogen transmission from contaminated product. Fresh fruit and produce could be contaminated by spoilage or pathogenic microorganisms during pre-harvest and post-harvest procedures (Brandl, 2006). It has also been indicated that the produce might become contaminated during production in the field or in the packing house (Brandl, 2006; Lynch, Tauxe, & Hedberg, 2009). There has been an increase in produce related outbreaks in recent years. Animals are the primary hosts of Salmonella enterica and the pathogen possesses genes to invade, survive host cells and resist immune defense mechanisms (Wallis & Galyov, 2000). Salmonella also has genes that confer fitness in non-host environments. The application of soil amended with manure produced by food animals could introduce foodborne pathogens in the farm environment (Hutchison, Walters, Moore, Crookes, & Avery, 2004). Several studies have demonstrated the persistence of Salmonella in the farm environment. The pathogen was detected in dairy farms, piggeries and slaughterhouse facilities both before and after slaughter (Baloda, Christensen, & Trajcevska, 2001; Hurd, McKean, Griffith, Wesley, & Rostagno, 2002; Millemann, Gaubert, Remy, & Colmin, 2000).
    [Show full text]