Foundation Systems for High-Rise Structures
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Gewerbeimmobilien, Baukultur Und Instagram Top 20 Instagram-Posts
Gewerbeimmobilien, Baukultur und Instagram Top 20 Instagram-Posts... ... der höchsten Wolkenkratzer Europas ... der Shopping-Center und Kaufhäuser 1 The Shard London #theshardlondon in Deutschland ... der Gewerbe- 2 Tour Montparnasse Paris #tourmontparnasse 1 KaDeWe Berlin #kadewe immobilien in Frankfurt 3 Main Tower Frankfurt #maintower 2 Bikini Berlin Berlin #bikiniberlin 1 Main Tower #maintower 4 Kulturpalast Warschau #palackulturyinauki 3 Mall of Berlin Berlin #mallofberlin 2 Europäische Zentralbank #ezb 5 Heron Tower London #herontower 4 My Zeil Frankfurt #myzeil 3 MyZeil #myzeil 6 Warsaw Spire Warschau #warsawspire 5 CentrO Oberhausen #centrooberhausen 4 Skyline Plaza #skylineplaza 7 DC Tower 1 Wien #dctower 6 Alsterhaus Hamburg #alsterhaus 5 Messe Turm #messeturm 8 Torre Unicredit Mailand #torreunicredit 7 Skyline Plaza Frankfurt #skylineplaza 6 Eurotower #eurotower 9 Messeturm Frankfurt #messeturm 8 Europa Passage Hamburg #europapassage 7 Commerzbank Tower #commerzbanktower 10 The Leadenhall Building London #leadenhallbuilding 9 Ruhr Park Bochum #ruhrpark 8 Japan Center #japancenter 11 One Canada Square London #onecanadasquare 10 Limbecker Platz Essen #limbeckerplatz 9 Campus Westend #campuswestend 12 Sky Tower Breslau #skytowerwroclaw 11 Oberpollinger München #oberpollinger 10 Tower 185 #tower185 13 Intempo Benidorm #intempo 12 Loop 5 Weiterstadt #loop5 11 Taunusturm #taunusturm 14 Commerzbank Tower Frankfurt #commerzbanktower 13 Thier-Galerie Dortmund #thiergalerie 12 Westhafen Tower #westhafentower 15 Torre Espacio Madrid #torreespacio -

LA VILLE > FRANCFORT
20 - 22 MARS 2015 > WE ART... FRANCFORT Grand Week-End art en liberté culminant à 259 mètres (299 avec l’antenne). Construite LA VILLE par l’architecte Norman Foster, elle dépasse de 2 mètres sa voisine la Messeturm, ancienne détentrice du record > FRANCFORT européen.Une autre tour intéressante : la tour Henninger (Henninger Turm), ancien silo de la Brasserie Henninger Francfort-sur-le-Main (Frankfurt am Main en allemand), est sur les hauteurs de Sachsenhausen au sud de la ville une ville d’Allemagne, généralement appelée simplement (un restaurant circulaire aujourd’hui fermé se trouve au Francfort malgré le risque de confusion avec la ville de sommet), est le premier bâtiment de la ville à dépasser les Francfort-sur-l’Oder. Située sur le Main, la ville est, avec 100 mètres de hauteur (elle en compte 110). Elle marque ses 700 000 habitants (les Francfortois), la cinquième ville en 1961 le début de la construction de gratte-ciel dans la d’Allemagne par sa population et la plus grande du Land cité, et détient le record de hauteur de la ville jusqu’en 1972 de Hesse. Près d’un habitant sur trois n’a pas la nationalité avec l’érection de l’AfE Turm. allemande. Son aire urbaine compte 2 517 561 habitants. Le centre ville de Francfort est très commerçant, Francfort est la 4e place financière et la 3e ville d’affaires notamment avec la Zeilstraße, dans laquelle se trouve la d’Europe ainsi que la ville la plus riche d’Allemagne avec Zeilgalerie (Centre commercial sur plusieurs étages) du un PIB par habitant de 85 300 euros. -
8. Nov 2014— 19. Apr 2015
Himmel- stürmend HOChhaUSSTADT FRANKFURT SKY WARD — HIGH-RIse CITY FRANKFURT G ruber + K leine- K raneburg: T aunusturm, 2011–2014 \ © G ruber + K leine- K raneburg \ Foto photo : K laus H elbig \ www.klaushelbig.de 8. NOV 2014— 19. APR 2015 ERÖFFNUNG DER AUSSTELLUNG Freitag, 7. November 2014, 19 Uhr EXHIBITION OPENING Friday, November 7, 2014, 7 p.m. Redner \ Speakers PETER CACHOLA SCHMAL, Direktor Director Deutsches Architekturmuseum (DAM) OLAF CUNITZ, Bürgermeister und Planungsdezernent, Stadt Frankfurt am Main Mayor and Head of Planning, City of Frankfurt PHILIPP STURM, Ausstellungskurator Exhibition Curator PRESSEKOnfEREnz Donnerstag, 6. November 2014, 11 Uhr \ PRess CONfeRENce Thursday, November 6, 2014, 11 a.m. FÜHrunGEN jeweils samstags und sonntags, 15 Uhr \ GUIDED TOURS on Saturdays and Sundays, 3 p.m. www.dam-online.de ABB Architekten: Deutsche-Bank-Hochhaus, 1978–1984 \ © Historisches Institut der Deutschen Bank Sprengung des AfE-Turms, Demonstration gegen Hausspekulanten im Westend, 1973 \ 2. Februar 2014 \ Blowing up the Murphy/Jahn: Messeturm, Demonstration against housing speculators in the Westend, 1973 \ AfE-Turm, February 2, 2014 \ © 1988–1991 \ © JAHN, Chicago Foto photo © DAM Archiv, Abisag Tüllmann Foto photo: Boris Zdravkovski Meixner Schlüter Wendt Architekten: Wohnhochhaus Henninger Turm, 2014–2016 \ © Meixner Schlüter Wendt Architekten Johannes Krahn: Bienenkorbhaus, 1953–1954 \ Institut für Stadtgeschichte Frankfurt am Main \ Foto photo: Klaus Meier-Ude Ludwig Mies van der Rohe: Entwurf für die Commerzbank, 1968 \ © 2014 MoMA, New York; Scala, Florenz Himmel- stürmend HOChhaUSSTADT FRANKFURT SKYWARD — HIGH-RISE CITY FRANKFURT Wie und warum wuchs Frankfurt in den Himmel? Dieser How and why did Frankfurt rise to such architectural Frage stellt sich die Ausstellung und bietet einen Überblick heights? The exhibition explores this question and offers zur Hochhausgeschichte der Stadt: Vom Wiederaufbau nach an overview of the history of the city’s high-rises. -

Innovating Sustainability 2011 Report
Innovating Sustainability 2011 Report “SEE”ingChange:2008ProgressReport a Business Roundtable (BRT) is an association of chief executive officers of leading U.S. companieswithnearly$6trillioninannualrevenuesandmorethan13millionemployees.BRT member companiescomprisenearlyathirdofthetotalvalueoftheU.S.stockmarketand invest morethan$114billionannuallyinresearchanddevelopment—nearlyhalfofallprivate U.S. R&Dspending.Ourcompaniespaymorethan$179billionindividendstoshareholders. BRT companiesgivenearly$9billionayearincombinedcharitablecontributions. Copyright©2011byBusinessRoundtable Innovating Sustainability 2011 Report April 2011 DEAR BUSINESSLEADERSANDSTAKEHOLDERS: On behalf of the members of Business Roundtable, I am proud to share with you Business Roundtable’s2011SustainabilityReport—Innovating Sustainability.n I it,youwillfindhow115 chief executiveofficersareaddressingsustainabilityusinginnovativeapproachesthataresmart business choicesandraisethequalityoflifeonourplanet.Sustainablebusinessstrategiesare no n longera option;theyarenowrootedinacorporation’scorebusinessplan. Each andeveryday,BusinessRoundtablemembercompaniesarechallengingthemselvestodo things better,smarterandwithresultsthatimprovethelifewelive.Theirsuccessstoriesare toldn i thisreport.Therangeofchallengesandopportunitiestheyfaceismetwithcreative, innovative thinkingthatsolvesproblemsandprovidesforprofitableeconomicgrowth—the essencef o asustainablebusiness. I hopeyouwillenjoyreadingInnovating Sustainability andlearningaboutthetechnologies, strategies andprogramsthatleadingU.S.companiesareusingtomaketheiroperationsandtheir -
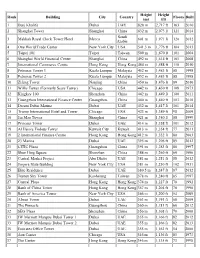
List of World's Tallest Buildings in the World
Height Height Rank Building City Country Floors Built (m) (ft) 1 Burj Khalifa Dubai UAE 828 m 2,717 ft 163 2010 2 Shanghai Tower Shanghai China 632 m 2,073 ft 121 2014 Saudi 3 Makkah Royal Clock Tower Hotel Mecca 601 m 1,971 ft 120 2012 Arabia 4 One World Trade Center New York City USA 541.3 m 1,776 ft 104 2013 5 Taipei 101 Taipei Taiwan 509 m 1,670 ft 101 2004 6 Shanghai World Financial Center Shanghai China 492 m 1,614 ft 101 2008 7 International Commerce Centre Hong Kong Hong Kong 484 m 1,588 ft 118 2010 8 Petronas Tower 1 Kuala Lumpur Malaysia 452 m 1,483 ft 88 1998 8 Petronas Tower 2 Kuala Lumpur Malaysia 452 m 1,483 ft 88 1998 10 Zifeng Tower Nanjing China 450 m 1,476 ft 89 2010 11 Willis Tower (Formerly Sears Tower) Chicago USA 442 m 1,450 ft 108 1973 12 Kingkey 100 Shenzhen China 442 m 1,449 ft 100 2011 13 Guangzhou International Finance Center Guangzhou China 440 m 1,440 ft 103 2010 14 Dream Dubai Marina Dubai UAE 432 m 1,417 ft 101 2014 15 Trump International Hotel and Tower Chicago USA 423 m 1,389 ft 98 2009 16 Jin Mao Tower Shanghai China 421 m 1,380 ft 88 1999 17 Princess Tower Dubai UAE 414 m 1,358 ft 101 2012 18 Al Hamra Firdous Tower Kuwait City Kuwait 413 m 1,354 ft 77 2011 19 2 International Finance Centre Hong Kong Hong Kong 412 m 1,352 ft 88 2003 20 23 Marina Dubai UAE 395 m 1,296 ft 89 2012 21 CITIC Plaza Guangzhou China 391 m 1,283 ft 80 1997 22 Shun Hing Square Shenzhen China 384 m 1,260 ft 69 1996 23 Central Market Project Abu Dhabi UAE 381 m 1,251 ft 88 2012 24 Empire State Building New York City USA 381 m 1,250 -

Commerzbank: the Social Tower
Commerzbank: The Social Tower September 1995 Many of us spend more time at our place of work than we do at home, so the nature of the workplace directly affects the quality of our lives - and indirectly that of our families. Some years ago many people were predicting the paperless office. That has proved to be a myth, despite the widespread use of computers and word processors. Today there is a similar myth, which suggests that we can all work at home and thereby eliminate the need for offices and corporate headquarters. Whilst the technology may exist to create such possibilities, the social needs for people to come together are very deeply rooted; notwithstanding teleconferencing, virtual reality and expanded horizons of private time for leisure. What is changing, however, is the level of our expectations. This is reflected in the so-called ‘green revolution’. We not only expect higher standards of comfort and amenity when we go to work, but we expect them to be created in a socially responsible manner, which will be mindful of the longer term consequences for future generations. The legislation and attitudes to such issues are more progressive in Germany than most other countries. In particular the climate of opinion in the city of Frankfurt further encourages the pursuit of higher design standards in both the public and private domain. To be socially responsible any building should work both from the outside in the civic context of its site, and from the inside, by responding to the special functions which generate the need for the building. -
Frankfurt Rheinmain 30.3. – 4.4.2014 Biennale Der Lichtkultur
Frankfurt RheinMain 30.3. – 4.4.2014 Biennale der Lichtkultur Biennale Lighting Culture Parallel zur www.luminale.de Impressum Grußwort Greetings www.luminale.de Liebe Luminale-Fans, Dear Luminale Fans, liebe Gäste, dear Guests, Redaktion es ist mir eine Freude, It is my pleasure to invite Helmut M. Bien Sie zur 7. Ausgabe der you to the 7th edition Angelika Kroll-Marth Luminale einzuladen. Als of Luminale, the Lighting Westermann Kommunikation Biennale der Lichtkultur Culture Biennale, which Gesellschaft für Publizistik mbH begleitet sie die Architek- accompanies the architec- Stiegelgasse 39 turmesse Light+Building. ture fair Light+Building. 55218 Ingelheim Frankfurt am Main wird in diesen Over the coming days, Frankfurt am Tagen zum international wichtigsten Main will be the most important Layout, Grafi k, Produktion Treffpunkt der Fachleute. Abends meeting place for experts from the Peter Sauer zieht es die Luminale-Besucher auf sector. In the evening Luminale visi- Messe Frankfurt Straßen und Plätze, um sich von tors fill the streets and squares of Medien und Service GmbH Kunstwerken, Design-Objekten, Publishing Services the city where they can enjoy works Ludwig-Erhard-Anlage 1 Performances und Licht-Klang-In- of art, design objects, performances 60327 Frankfurt am Main stallationen faszinieren zu lassen. and light and sound installations. Zur Luminale öffnet sich die Stadt During Luminale, the city becomes Sanart Grafi k Design, Bad Vilbel den Kreativen als Experimentierfeld. an experimental proving ground for Dieser Labor-Charakter unterscheidet creative personalities. This labora- Übersetzung die Luminale von der Vielzahl der tory character distinguishes Veronica Özbakir, Bad Vilbel Lichtfestivals, die – nicht zuletzt Luminale from the numerous other inspiriert durch den Erfolg der lighting festivals, many of which are Litho Luminale – mit Licht Leute in ihre inspired by the success of Luminale Reproduktion45, Frankfurt am Main Innenstädte locken. -

EBRD Trade Facilitation Programme Confirming Banks
EBRD Trade Facilitation Programme Confirming Banks Table of Contents (Click on a country heading to go to that section) Algeria ...................................................................................................................................................... 4 Angola...................................................................................................................................................... 4 Argentina ................................................................................................................................................. 4 Armenia ................................................................................................................................................... 4 Australia ................................................................................................................................................... 4 Austria ...................................................................................................................................................... 5 Azerbaijan ................................................................................................................................................ 6 Bahrain .................................................................................................................................................... 6 Bangladesh .............................................................................................................................................. 6 Belarus.................................................................................................................................................... -

Analyzing Passive Solar Strategies in the Case of High-Rise Building
Renewable and Sustainable Energy Reviews 52 (2015) 1340–1353 Contents lists available at ScienceDirect Renewable and Sustainable Energy Reviews journal homepage: www.elsevier.com/locate/rser Analyzing passive solar strategies in the case of high-rise building Pooya Lotfabadi n Faculty of Architecture, Eastern Mediterranean University, Via Mersin 10, Famagusta, North Cyprus, Turkey article info abstract Article history: Nowadays, societies are not able to live without energy. After 1970's energy crises, energy has become a Received 3 December 2014 more serious issue and environmental protection is one of the most important considerations in Received in revised form countries' sustainable development. Different types of energies such as thermal, electricity and so on are 25 May 2015 used in people's daily lives. Many of these energy types are derived from sedimentary sources like oil, Accepted 29 July 2015 gas and coal, which are not interminable. So, one of the fundamental challenges of today's world is seeking renewable energy alternatives such as solar, wind, hydro, biomass, geothermal and so on, to Keywords: replace the fossil fuels. This attempt should be done in all sections like transportation, industry, buildings High-rise buildings and etc. Building section is one of the greatest energy consumer sectors. In this sector, high-rise Renewable energies buildings with their vast facades have a great potential to consume sustainable energies. For instance Passive solar strategies they can easily gain solar radiations. Thus, here, the emphasis has been put on the practices and attempts Frankfurt Commerzbank done to take advantages of solar radiation as an energy source in high-rise buildings. -

Megacities – Megarisks Trends and Challenges for Insurance and Risk Management Traffic and Spatial Problems in Megacities Pose a Special Challenge for City Planners
Knowledge series Megacities – Megarisks Trends and challenges for insurance and risk management Traffic and spatial problems in megacities pose a special challenge for city planners. These problems can only be overcome by designing unconventional structures, as illustrated here by the city freeway in Shanghai. Earthquake catastrophes have shown, however, that bridges and flyovers are often highly prone to losses. Munich Re, Megacities – Megarisks Foreword Global urbanisation and rural-to-urban migration are among the megatrends of our time – together with population growth, the overexploitation of natural resources, environmental pollution and globalisation – that will have the most lasting impact on the future of mankind. However, as with other developments, even a model for success – as cities undoubtedly are in view of their positive influence on culture, economic activity, technologies and networks – will even- tually reach its limits and, once the negative effects exceed the positive ones, necessitate a change in paradigm. A megacity is a prime example of such a critical stage of development: an organism with more than ten million living cells gradually risks being suffo- cated by the problems it has itself created – like traffic, environmental damage and crime. This is especially true where growth is too rapid and unorganic, as is the case in most megacities in emerging and developing countries. As the trend towards megacities gathers pace, opportunities and risks go hand in hand and undergo major changes over time. Munich Re therefore began to consider these problems at an early stage, beginning in the 1990s and gradually examining a series of important aspects in its publications. -

Technical Developments in High-Rise Building
22nd International Symposium on Automation and Robotics in Construction 1 ISARC 2005 - September 11-14, 2005, Ferrara (Italy) Technical developments in high-rise building Ger Maas, professor at the Faculty of Building, Architecture and Planning, Eindhoven University of Technology, PO Box 513, 5600 MB Eindhoven, the Netherlands and Director of Strategy of Royal BAM Group, the Netherlands, [email protected] This research was conducted in 2004 and 2005 by the Abstract- What are the considerations when opting for high-rise Construction Management and Engineering Research Group building? What construction techniques for the logistics are of Eindhoven University of Technology [3]. applied in Europe? What ecological innovations are applied? What are the technical conditions for combined use of high-rise building seen from a vertical point of view? What are the II. RESEARCH QUESTIONS differences in technical aspects of high-rise construction in the The research questions concern: world? What are the market differences between the continents? 1) Necessary changes in the performance of High Rise Building Index Terms—High-rise building, development, clients, 2) Developments in Production Systems differences between continents, combined use in a vertical way, 3) The Construction Management approach innovations, ecology. According to this categorisation, the various detail questions will be dealt with in Chapter IV. I. INTRODUCTION HIS is a report of the results of a large-scale study of III. RESEARCH METHOD technical developments in the construction of high-rise T The research was conducted between November 2004 and projects. The spread of the world’s population is changing and March 2005. -

MESSETURM Image Book 121120.Pdf
Discover a new AMAZING POINT of view Facts and FIGURES Completion date 1990 Height 257 M Floors 63 Base area 62.000 SQ M Entrance foyer 15 M HIGH Floor Area 41 x 41 SQ M 22 PASSENGER LIFTS Multi-storey car park WITH APPROX. 900 PARKING SPACES BELOW THE MESSETURM TOWER Direct access to the underground railway IN THE BUILDING Access controlled via turnstile system WITH CARD READERS Leed Silver BUILDING CERTIFICATION The Landmark Ganz gleich, ob man sich Frankfurt über die Autobahn nähert, im Anflug auf den Flughafen aus dem Fenster schaut oder mit dem Zug über eine der Brücken in die Metropole am Main fährt – der erste Blick fällt immer auf die Skyline mit ihrer selbstbewussten Präsenz. Ein Hochhaus hebt sich dabei deutlich sichtbar von allen anderen ab: der Messeturm. Von Stararchitekt Helmut Jahn geplant und von 1988 bis 1991 errichtet, setzte das damals höchste Gebäude Europas eine Benchmark und ist noch heute ein Wahrzeichen, das einen besonderen Platz im Bild der Stadt und in den Herzen der Menschen einnimmt. Kein Wunder, denn der Messeturm hat Außergewöhnliches zu bieten: Eine ikonische Form, die an Some are known, Art-déco-Legenden wie das Chrysler-Building oder Empire State Building erinnert. Eine fantastische Lage. Die Exklusivi- tät einer eigenen Postleitzahl. Und das spannende Format eines Klassikers, der jetzt ein neues Kapitel aufschlägt. Regardless of whether you approach Frankfurt from the motorway, look out of the window of an aeroplane, ONLY ONE or cross one of the bridges by train, the first thing you will see is the skyline and its commanding presence.