Analog MIMO Spatial Filtering
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Cell Phones and Pdas
eCycle Group - Check Prices Page 1 of 19 Track Your Shipment *** Introductory Print Cartridge Version Not Accepted February 4, 2010, 2:18 pm Print Check List *** We pay .10 cents for all cell phones NOT on the list *** To receive the most for your phones, they must include the battery and back cover. Model Price Apple Apple iPhone (16GB) $50.00 Apple iPhone (16GB) 3G $75.00 Apple iPhone (32GB) 3G $75.00 Apple iPhone (4GB) $20.00 Apple iPhone (8GB) $40.00 Apple iPhone (8GB) 3G $75.00 Audiovox Audiovox CDM-8930 $2.00 Audiovox PPC-6600KIT $1.00 Audiovox PPC-6601 $1.00 Audiovox PPC-6601KIT $1.00 Audiovox PPC-6700 $2.00 Audiovox PPC-XV6700 $5.00 Audiovox SMT-5500 $1.00 Audiovox SMT-5600 $1.00 Audiovox XV-6600WOC $2.00 Audiovox XV-6700 $3.00 Blackberry Blackberry 5790 $1.00 Blackberry 7100G $1.00 Blackberry 7100T $1.00 Blackberry 7105T $1.00 Blackberry 7130C $2.00 http://www.ecyclegroup.com/checkprices.php?content=cell 2/4/2010 eCycle Group - Check Prices Page 2 of 19 Search for Pricing Blackberry 7130G $2.50 Blackberry 7290 $3.00 Blackberry 8100 $19.00 Blackberry 8110 $18.00 Blackberry 8120 $19.00 Blackberry 8130 $2.50 Blackberry 8130C $6.00 Blackberry 8220 $22.00 Blackberry 8230 $15.00 Blackberry 8300 $23.00 Blackberry 8310 $23.00 Blackberry 8320 $28.00 Blackberry 8330 $5.00 Blackberry 8350 $20.00 Blackberry 8350i $45.00 Blackberry 8520 $35.00 Blackberry 8700C $6.50 Blackberry 8700G $8.50 Blackberry 8700R $7.50 Blackberry 8700V $6.00 Blackberry 8703 $1.00 Blackberry 8703E $1.50 Blackberry 8705G $1.00 Blackberry 8707G $5.00 Blackberry 8707V -

Nokia in 3Q 2003 Word Document
1 (15) PRESS RELEASE October 16, 2003 Strong volume growth and excellent profitability in mobile phones - Nokia meets third-quarter sales and EPS targets Highlights: 3Q 2003 (all comparisons are year on year) • Net sales declined 5% to EUR 6.9 billion (up 4% at constant currency). • Nokia Mobile Phones sales were flat at EUR 5.6 billion (up 9% at constant currency). • Nokia Networks sales declined 21% to EUR 1.2 billion. • Nokia gains market share with 23% volume growth; industry mobile phone volume growth accelerates to 15%. • Nokia third-quarter mobile phone market share grows to 39%. • Company doubles share of global CDMA handset market. • Excellent pro forma and reported operating margins in mobile phones at 22.4% and 22.0%. • Nokia Networks achieves breakeven. • Nokia announces new operating structure for 2004. • Pro forma EPS (diluted) was EUR 0.18. Reported EPS (diluted) was EUR 0.17. • Strong operating cash flow in the third quarter at EUR 1.2 billion. JORMA OLLILA, CHAIRMAN AND CEO: The third quarter brought a sharp increase in mobile phone volumes for Nokia. Mobile phone market volumes rose an impressive 15% year on year for the quarter to 118 million units, while Nokia’s own volume growth accelerated even more sharply, rising by 23% to 45.5 million units. The mobile phone market has continued to strengthen throughout the year, and we now expect overall industry volume for 2003 to be about 460 million units. During the quarter, we saw our overall mobile phone market share rise to 39%, up from 36% in the same quarter last year. -

Advantage Cartridge Cell Phone Price List Effective 2-1-12 Click Here to See Shipping Instructions
Advantage Cartridge Cell Phone Price List Effective 2-1-12 Click here to see Shipping Instructions We pay .25 for all cell phones not on this list, as well as damaged phones unless a higher price is listed below. • Broken cell phones do not qualify for payment. A phone is considered broken when it is in pieces • Damaged phones are phones with broken screen, water damage, and does not power up. ALCATEL A800 $ 0.30 ALCATEL A808 $ 0.30 APPLE iPhone 2G $ 25.00 APPLE iPhone 2G Damage $ 5.00 APPLE iPhone 2G $ 25.00 APPLE iPhone 3G 16GB Damage $ 10.00 APPLE iPhone 3G 16GB $ 50.00 APPLE iPhone 3G 8GB Damage $ 8.00 APPLE iPhone 3G 8GB $ 40.00 APPLE iPhone 3GS 16GB Damage $ 25.00 APPLE iPhone 3GS 16GB $ 125.00 APPLE iPhone 3GS 32GB Damage $ 30.00 APPLE iPhone 3GS 32GB $ 150.00 APPLE iPhone 3GS 8GB Damage $ 18.00 APPLE iPhone 3GS 8GB $ 90.00 APPLE iPhone 4C 16GB Damage $ 30.00 APPLE iPhone 4C 16GB $ 150.00 APPLE iPhone 4C 32GB Damage $ 35.00 APPLE iPhone 4C 32GB $ 175.00 APPLE iPhone 4G 16GB Damage $ 30.00 APPLE iPhone 4G 16GB $ 150.00 APPLE iPhone 4G 32GB Damage $ 35.00 APPLE iPhone 4G 32GB $ 175.00 APPLE iPhone 4S 16GB Damage $ 40.00 APPLE iPhone 4S 16GB $ 200.00 APPLE iPhone 4S 32GB Damage $ 60.00 APPLE iPhone 4S 32GB $ 300.00 BLACKBERRY 6210 $ 0.30 BLACKBERRY 6230 $ 0.30 BLACKBERRY 6280 $ 0.30 BLACKBERRY 7100R $ 0.30 BLACKBERRY 7100T $ 0.30 BLACKBERRY 7100V $ 0.30 BLACKBERRY 7100X $ 0.30 BLACKBERRY 7105T $ 0.30 BLACKBERRY 7130C $ 0.30 BLACKBERRY 7130G $ 0.30 BLACKBERRY 7130V $ 0.30 BLACKBERRY 7270 $ 0.30 BLACKBERRY 7290 $ 1.50 BLACKBERRY 7510 -
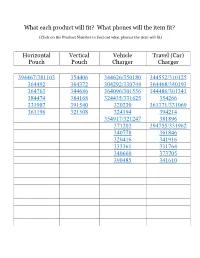
What Each Product Will Fit? What Phones Will the Item Fit?
What each product will fit? What phones will the item fit? (Click on the Product Number to find out what phones the item will fit) Horizontal Vertical Vehicle Travel (Car) Pouch Pouch Charger Charger 394467/381103 354406 344626/350180 344552/310125 364492 364372 304292/330744 364468/340193 364763 344686 364096/301556 344486/301343 384474 384168 324435/331625 354266 331907 391540 320230 361371/331069 361196 321508 324194 394214 354917/321247 381896 371203 394755/331962 340778 361846 320416 341916 333361 331764 340660 373705 390485 341610 Horizontal Pouch: 394467/381103 BLACKBERRY 8110 HTC Fuze HTC Touch Pro (CDMA HTC Touch Pro (CDMA) HTC Touch Pro (GSM) Verizon) LG CU720 Shine MOTOROLA MOTORAZR V3xx LG CT810 Incite MOTOROLA MOTORAZR V3xx Gray MOTOROLA MOTORAZR Platinum MOTOROLA MOTORAZR V3xx V3xx Pink MOTOROLA VA76r Tundra Ruby Red MOTOROLA RAZR V3 NOKIA 6085 NOKIA 2600 NOKIA 2610 NOKIA 6555 Red NOKIA 6102i NOKIA 6103 NOKIA RAM NOKIA 6555 Sand NOKIA 6650 PANTECH C740 Matrix PANTECH C520 Breeze PANTECH C610 RIM BLACKBERRY 8110 PANTECH C810 PANTECH C810 DUO SAMSUNG SGH-A437 Gold SAMSUNG SGH-A127 SAMSUNG SGH-A137 SAMSUNG SGH-A727 SAMSUNG SGH-A437 Red SAMSUNG SGH-A437 Slate SONY ERICSSON C905 SAMSUNG SGH-A767 Propel SAMSUNG SGH-A777 SONY ERICSSON W580i Gray SONY ERICSSON W350 SONY ERICSSON W580i Black SONY ERICSSON Z310a Jet Black SONY ERICSSON W580i White SONY ERICSSON W760i SONY ERICSSON Z780a SONY ERICSSON Z310a Lush SONY ERICSSON Z750a Pink 364492 APPLE iPhone BLACKBERRY 8310 Curve BLACKBERRY 8700g BLACKBERRY 8820 BLACKBERRY 8900 BLACKBERRY -

Mobile Phone Based Remote Monitoring System
Mobile Phone based Remote Monitoring System by Danyi Liu A Thesis Submitted in Fulfilment of the Degree of Master of Engineering Auckland University of Technology Auckland June 2008 Acknowledgements I wish to express my gratitude to my supervisor, Professor Adnan Al-Anbuky, for his ongoing guidance, his patience, his excellent advice, and most of all his kind understanding. His high expectations of me encouraged me to perform the best that I could and I respect him for that. I would also like to express my gratitude to Dr. Lin Chen, who had been my co- supervisor for one semester, for his patience and his good advice. I would also like to thank Murray McGovern at Mobile Control Solutions Ltd for his technical and project support. His help has been very valuable. Thanks also to Mr. Hong Zhang at MCS and to Sean Tindle, both of whom tolerated me and aided me in my quest so supportively. Thanks to David Parker for his proof reading of my work and his advice. I appreciate also, so much, my family’s interest and encouragement, without which I would not have had this opportunity. i Abstract This thesis investigates embedded databases and graphical interfaces for the MicroBaseJ project. The project aim is the development of an integrated database and GUI user interface for a typical 3G, or 2.5G, mobile phone with Java MIDP2 capability. This includes methods for data acquisition, mobile data and information communication, data management, and remote user interface. Support of phone delivered informatics will require integrated server and networking infrastructure research and development to support effective and timely delivery of data for incorporation in mobile device-based informatics applications. -

MIR Centrum Komputerowe
Informacje o produkcie Utworzono 26-09-2021 Etui/Kabura Magnum Gazeta Model 3 4mobile GSM Cena : 11,99 zł Nr katalogowy : 6420 Stan magazynowy : brak w magazynie Średnia ocena : brak recenzji Pasuje do: Alcatel 153 Alcatel OT301 Alcatel OT302 Alcatel OT311 Alcatel OT320 Alcatel OT535 Alcatel OT557 Alcatel OT565 Alcatel OT735 Alcatel OT735i Alcatel OT756 Alcatel OT757 Alcatel OT-S853 LG B1200 LG B1300 LG B2000 LG C3100 LG C3400 LG G1500 LG G1600 LG G1610 LG G1700 LG g1800 LG G3100 MIR Centrum Komputerowe LG G5300 LG G5310 LG L3100 LG L341i Mitsubishi M320 Mitsubishi M350 Motorola C155 Motorola C200 Motorola C205 Motorola C230 Motorola C380 Motorola C385 Motorola C390 Motorola E1 Motorola E365 Motorola E375 Motorola E390 Motorola E398 Wygenerowano w programie www.oscGold.com Motorola K1 KRZR Motorola rokr E1 Motorola V600 Motorola Z3 Motorola Z6 Siemens A50 Siemens A53 Nokia 1100 Nokia 1101 Nokia 1110 Nokia 1116 Nokia 1208 Nokia 1209 Nokia 1600 Nokia 1650 Nokia 2100 Nokia 2300 Nokia 2310 Nokia 2600 Nokia 2610 Nokia 2630 Nokia 2865 Nokia 3100 Nokia 3108 Nokia 3120 Nokia 3200 Nokia 3220 Nokia 3230 Nokia 3610 Nokia 5070 Nokia 5140 Nokia 5140i Nokia 5210 Nokia 5310 XpressMusic Nokia 5500 Sport Nokia 6020 Nokia 6021 Nokia 6070 Nokia 6080 Nokia 6108 Nokia 6121 classic Nokia 6151 Nokia 6220 Nokia 6230 Nokia 6230i Nokia 6233 Nokia 6234 Nokia 6270 Nokia 6282 Nokia 6610 Nokia 6610i Nokia 6820 Nokia 6822 Nokia 7210C Nokia 7250 Nokia 7250i MIR Centrum Komputerowe Nokia 7260 Nokia 7360 Nokia 8800 Nokia 8810 Nokia 8910 Nokia 8910i Nokia E65 Sagem MW3020 -
Nokia in 2003 Annual Accounts
NOKIA IN 2003 NNokiaokia iinn 20032003 kkannetannet 1 112.3.20042.3.2004 111:07:291:07:29 NNokiaokia iinn 20032003 kkannetannet 2 112.3.20042.3.2004 111:07:331:07:33 A N N U A L A C C O U N T S 2 0 0 3 Key data 2003 4 Review by the Board of Directors 5 Consolidated profit and loss accounts, IAS 8 Consolidated balance sheets, IAS 9 Consolidated cash flow statements, IAS 10 Statements of changes in shareholders’ equity, IAS 12 Notes to the consolidated financial statements 13 Profit and loss accounts, parent company, FAS 32 Cash flow statements, parent company, FAS 32 Balance sheets, parent company, FAS 33 Notes to the financial statements of the parent company 34 Nokia shares and shareholders 38 Nokia 1999–2003, IAS 45 Calculation of key ratios 48 Proposal by the Board of Directors to the Annual General Meeting 49 Auditors’ report 50 A D D I T I O N A L I N F O R M A T I O N U.S. GAAP 52 Critical accounting policies 55 Group Executive Board 58 Board of Directors 60 Risk factors 62 Corporate Governance 63 Investor information 68 General contact information 69 Nokia in 2003 | 3 NOKIA IN 2003_s03-16 3 8.3.2004, 13:09 Key data 2003 NOKIA 2003 2002 Change, % 2001 EURm The key data is based on Net sales 29 455 30 016 –2 31 191 financial statements according Operating profit 5 011 4 780 5 3 362 to International Accounting Profit before taxes 5 345 4 917 9 93 475 Standards, IAS Net profit 3 592 3 381 6 2 200 Research and development 3 760 3 052 23 2 985 Return on capital employed, % 34.7 35.3 27.9 Net dept to equity (gearing), % –71 –61 –41 EUR -
Nokia's Form 20-F 2003
NOKIA FORM 20–F 2003 As filed with the Securities and Exchange Commission on February 6, 2004. SECURITIES AND EXCHANGE COMMISSION Washington, D.C. 20549 FORM 20-F ANNUAL REPORT PURSUANT TO SECTION 13 OR 15(D) OF THE SECURITIES EXCHANGE ACT OF 1934 For the fiscal year ended December 31, 2003 Commission file number 1-13202 Nokia Corporation (Exact name of Registrant as specified in its charter) Republic of Finland (Jurisdiction of incorporation) Keilalahdentie 4, P.O. Box 226, FIN-00045 NOKIA GROUP, Espoo, Finland (Address of principal executive offices) Securities registered pursuant to Section 12(b) of the Act: Name of each exchange Title of each class on which registered American Depositary Shares New York Stock Exchange Shares, par value EUR 0.06 New York Stock Exchange(1) (1) Not for trading, but only in connection with the registration of American Depositary Shares representing these shares, pursuant to the requirements of the Securities and Exchange Commission. Securities registered pursuant to Section 12(g) of the Act: None Securities for which there is a reporting obligation pursuant to Section 15(d) of the Act: None Indicate the number of outstanding shares of each of the registrant’s classes of capital or common stock as of the close of the period covered by the annual report. Shares, par value EUR 0.06: 4 796 292 460 Indicate by check mark whether the registrant: (1) has filed all reports required to be filed by Section 13 or 15(d) of the Securities Exchange Act of 1934 during the preceding 12 months (or for such shorter period that the registrant was required to file such reports), and (2) has been subject to such filing requirements for the past 90 days. -
Nokia Corporation ;
i ~ . UNITED STATES DISTRICT COURT FOR THE SOUTHERN DISTRICT OF NEW YORK IN RE NOKIA OYJ (NOKIA CORP.) CASE NO. 04 Civ. 2646 (KAK) SECURITIES LITIGATION CONSOLIDATED CLASS ACTION COMPLAINT FOR VIOLATIONS OF FEDERAL SECURITIES LAWS JURY TRIAL DEMANDE D Lead plaintiffs Generic Trading of Philadelphia, LLC ("Generic"), Martin Bergljung an d Gerald Hoberman, by their attorneys, for their Consolidated Class Action Complaint (th e "Complaint") allege the following based upon knowledge with respect to their own acts and upo n other facts obtained through an investigation made by and through plaintiffs' counsel, whic h included a review of United States Securities and Exchange Commission ("SEC") filings b y Nokia OYJ (Nokia Corp.) ("Nokia" or the "Company"), as well as securities analysts reports and advisories about the Company, press releases, analyst conference calls, and other publi c statements issued by the Company and posted on their website, media reports about the Company and information learned from interviews of Nokia former employees and other knowledgeabl e persons. Based upon the substantial facts already uncovered, plaintiffs believe that substantia l additional evidentiary support will exist for the allegations set forth herein after a reasonabl e opportunity for discovery. 2498821 NATURE OF THE ACTIO N This is a securities class action on behalf of purchasers of the securities of Noki a between October 16, 2003 and April 15, 2004 (the "Class Period"), seeking to pursue remedie s under the Securities Exchange Act of 1934 (the "Exchange Act") 2 . Defendant Nokia is a Finnish limited liability company with its executive office s located at Keilalahdentie 4, FIN-00045 Nokia Group, P .O. -

Report for Ofcom on the Value of Ultra Wide Band Personal Area Networking Services to the United Kingdom
Value of UWB Personal Area Networking Services to the United Kingdom Final Report for Ofcom This report was commissioned by Ofcom to provide an independent analysis of the costs and benefits which are likely to be associated with the deployment of UWB technology in the United Kingdom, in order to assist Ofcom in its development of policy in this area. The assumptions, conclusions and recommendations expressed in this report are entirely those of Mason and DotEcon and should not be attributed to Ofcom. Mason Communications Ltd 20-23 Greville Street London EC1N 8SS England Tel: +44 (0) 20 7336 8255 Fax: +44 (0) 20 7336 8256 e-mail: [email protected] www.mason.biz DotEcon Ltd 105-106 New Bond Street London W1S 1DN ENGLAND TEL: +44 (0) 20 7870 3800 FAX: +44 (0) 20 7870 3811 www.dotecon.com November 2004 FINAL REPORT FOR OFCOM VALUE OF UWB PERSONAL AREA NETWORKING SERVICES TO THE UNITED KINGDOM MASON COMMUNICATIONS LTD 20-23 GREVILLE STREET, LONDON EC1N 8SS. ENGLAND TEL: +44 (0) 20 7336 8255 FAX: +44 (0) 20 7336 8256 e-mail: [email protected] www.mason.biz DOTECON LIMITED 105-106 NEW BOND STREET, LONDON W1S 1DN, ENGLAND TEL: +44 (0)20 7870 3000 FAX +44 (0)20 7870 3811 www.dotecon.com CONTENTS EXECUTIVE SUMMARY .......................................................................................................3 1. INTRODUCTION ............................................................................................................10 1.1 Study Objectives......................................................................................................10 -

NTC Type Approval No. Type of Equipment Brand/Model Marketing
LIST OF CUSTOMER PREMISES EQUIPMENT (CPE) G WC LT G NTC Type Approval No. Type of Equipment Brand/Model Marketing Name Integrated Module S DM Date Issued Applicant E PS M A ESD-CPE-1502962 HP / SIC 1ADSL; HP MSR 1-port ADSL2+ SIC Module (JD537A) 1-Port ADSL2+ SIC Module 04/14/2015 HP (Phils) Corporation ESD-CPE-1502993 1-Port E1 Voice Interface Module 1-port Voice E1 SIC Module 06/17/2015 HEWLETT PACKARD PHILIPPINES CORP. ESD-CPE-1603171 GSM Gateway with ISDN PRI Interface 2N / 2N® StarGate x 12/15/2016 CHALLENGE SYSTEMS INCORPORATED ESD-CPE-1102359 PABX with Cinterion MC55i GSM/GPRS Module 2N NetStar 03/14/2011 Wordtext Systems, Inc. ESD-CPE-1603171 GSM Gateway with ISDN PRI Interface 2N StarGate x 07/28/2016 Logic Solutions Inc ESD-CPE-1603155 GSM/GPRS VOIP Gateway 2N TELEKOMUNIKACE a.s / 2N StarGate x x 05/24/2016 Cognetics Inc ESD-CPE-1603220 VoiP GSM/WCDMA Gateway 2N TELEKOMUNIKACE a.s / 2N VoiceBlue MAX x x 11/08/2016 COGNETICS INC ESD-CPE-0100243 DATA MODEM 3C3FEM656c 3COM 10/100 LAN + 56K 05/16/2001 3COM PHILIPPINES, INC. ESD-CPE-0000173 MODEM 3COM 10/100 LAN +56K Global Modem CardBus PC Card 01/31/2000 3COM PHILIPPINES, INC. ESD-CPE-0100242 KEY TELEPHONE 3COM NBX 100 07/12/2001 3COM PHILIPPINES, INC. ESD-CPE-0000172 MODEM 3COM US ROBOTICS 56K FAX Modem USB 01/04/2001 3COM PHILIPPINES, INC. ESD-CPE-0801880 ADSL Modem 3COM WL-603 09/19/2008 3COM Corporation ESD-CPE-1703247 End Device Router with GSM/WCDMA/HSPA+ Module 3CSN/3CW4G x x 03/23/2017 3C Enterprise IP Pty Ltd Australia ESD-CPE-0200330 DATA MODEM 802.11b Wireless Ethernet + AC'97 Modem PCI Type IIIA Adapter Model: M3AWEB56GA 04/26/2002 Intel Microelectronics Philippines, Inc. -

Nokia 3200 User Guide
3200.ENv1_9310067.book Page 1 Thursday, September 18, 2003 8:42 AM Nokia 3200 User Guide What information is Numbers Where is the number? needed? My number Wireless service provider Voice mail number Wireless service provider Wireless provider’s number Wireless service provider Provider’s customer care Wireless service provider 3200 Label on back of phone Model number (under battery) Label on back of phone Phone type (under battery) Label on back of phone International mobile (under battery). See “Find equipment identity (IMEI) information about your phone” on page 8. 3200.ENv1_9310067.book Page 2 Thursday, September 18, 2003 8:42 AM LEGAL INFORMATION Part No. 9310067, Issue No. 1 Copyright © 2003 Nokia. All rights reserved. Nokia, Nokia Connecting People, Nokia 3200, Pop-Port, and the Nokia Original Enhancements logos are trademarks or registered trademarks of Nokia Corporation. Other company and product names mentioned herein may be trademarks or trade names of their respective owners. Printed in Canada 09/2003 T9 text input software Copyright © 1999-2003. Tegic Communications, Inc. All rights reserved. Includes RSA BSAFE cryptographic or security protocol software from RSA Security. Java is a trademark of Sun Microsystems, Inc. The information contained in this user guide was written for the Nokia 3200 product. Nokia operates a policy of ongoing development. Nokia reserves the right to make changes to any of the products described in this document without prior notice. UNDER NO CIRCUMSTANCES SHALL NOKIA BE RESPONSIBLE FOR ANY LOSS OF DATA OR INCOME OR ANY SPECIAL, INCIDENTAL, AND CONSEQUENTIAL OR INDIRECT DAMAGES HOWSOEVER CAUSED. THE CONTENTS OF THIS DOCUMENT ARE PROVIDED "AS IS." EXCEPT AS REQUIRED BY APPLICABLE LAW, NO WARRANTIES OF ANY KIND, EITHER EXPRESS OR IMPLIED, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE, ARE MADE IN RELATION TO THE ACCURACY AND RELIABILITY OR CONTENTS OF THIS DOCUMENT.