Fundamentals of Pure Mathematics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Pure Mathematics Professors Teaching and Leading Research CO-OP OR REGULAR 28
PURE MATHEMATICS Pure Mathematics professors teaching and leading research CO-OP OR REGULAR 28 Mathematician ranked among top 10 TOP 10 jobs from 2011-2017 – Comcast.com of grads are employed Search for a deeper 96.6% within 2 years understanding of mathematics Pure mathematics is at the foundation of all mathematical reasoning. If first-year calculus ALEX teaches you how to drive the car, Pure Mathematics teaches you how to build one. 3B, PURE MATHEMATICS AND Mathematicians know that there could be no general relativity without differential COMBINATORICS AND geometry, and no computer security without advanced number theory. OPTIMIZATION Pure Mathematics at Waterloo is a small, cohesive, and challenging program that will open countless doors for you. Our graduates have used the program as a springboard into careers WHAT DO YOU LOVE ABOUT in information technology, finance, business, science, education, and insurance, often by way PURE MATHEMATICS? The satisfaction from understanding of some of the most prestigious graduate programs in the world. an idea at a deeper level and tying together unrelated branches of ALEX’S FAVOURITE COURSES mathematics or physics for the › PMATH 320 Euclidean Geometry: This course is everything you love about Geometry: first time is the most rewarding Euclid’s axioms, isometries of the Euclidean plane and of Euclidean space, polygons, part of learning and understanding polyhedral, polytopes, and the kissing problem. mathematics. What I really enjoy is › PMATH 351 Real Analysis: It’s a very intuitive and natural approach to real analysis, and the developing a deep understanding of complexity of the course builds very naturally to the end of the semester. -

Pure Mathematics
Why Study Mathematics? Mathematics reveals hidden patterns that help us understand the world around us. Now much more than arithmetic and geometry, mathematics today is a diverse discipline that deals with data, measurements, and observations from science; with inference, deduction, and proof; and with mathematical models of natural phenomena, of human behavior, and social systems. The process of "doing" mathematics is far more than just calculation or deduction; it involves observation of patterns, testing of conjectures, and estimation of results. As a practical matter, mathematics is a science of pattern and order. Its domain is not molecules or cells, but numbers, chance, form, algorithms, and change. As a science of abstract objects, mathematics relies on logic rather than on observation as its standard of truth, yet employs observation, simulation, and even experimentation as means of discovering truth. The special role of mathematics in education is a consequence of its universal applicability. The results of mathematics--theorems and theories--are both significant and useful; the best results are also elegant and deep. Through its theorems, mathematics offers science both a foundation of truth and a standard of certainty. In addition to theorems and theories, mathematics offers distinctive modes of thought which are both versatile and powerful, including modeling, abstraction, optimization, logical analysis, inference from data, and use of symbols. Mathematics, as a major intellectual tradition, is a subject appreciated as much for its beauty as for its power. The enduring qualities of such abstract concepts as symmetry, proof, and change have been developed through 3,000 years of intellectual effort. Like language, religion, and music, mathematics is a universal part of human culture. -
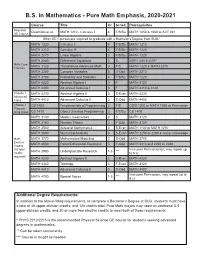
B.S. in Mathematics - Pure Math Emphasis, 2020-2021
B.S. in Mathematics - Pure Math Emphasis, 2020-2021 Course Title Cr. Sched. Prerequisites Required Quantitative Lit. MATH 1210 - Calculus I 4 F/S/Su MATH 1050 & 1060 or ACT 26+ GE Course Other GE Courses are required to graduate with a Bachelor’s Degree from SUU.* MATH 1220 Calculus II 4 F/S/Su MATH 1210 MATH 2210 Calculus III 4 F/S/Su MATH 1220 MATH 2270 Linear Algebra 3 F/S/Su MATH 1220 MATH 2280 Differential Equations 3 S MATH 1220 & 2270** Math Core MATH 3120 Transition to Advanced Math 3 F/S MATH 1220 & MATH 2270 Courses MATH 3250 Complex Variables 3 S-Odd MATH 2210 MATH 3700 Probability and Statistics 4 F/S/Su MATH 1220 MATH 4220 Abstract Algebra I 3 F MATH 3120 MATH 4400 Advanced Calculus I 3 F MATH 2210 & 3120 Choose 1 MATH 4230 Abstract Algebra II 3 S-Even MATH 4220 Advanced Class MATH 4410 Advanced Calculus II 3 S-Odd MATH 4400 Choose 1 CS 1400 Fundamentals of Programming 3 F/S CSIS 1030 or MATH 1050 or Permission Program- ming Class CS 1410 Object Oriented Programming 3 F/S/Su CS 1400 MATH 3130 Modern Geometries 3 S MATH 3120 MATH 3160 Number Theory 3 F-Odd MATH 3120 MATH 3500 Actuarial Mathematics 3 S-Even MATH 1100 or MATH 1210 MATH 3600 Numerical Analysis 3 S-Even MATH 2250 or 2280 & comp. knowledge Math MATH 3770 Mathematical Modeling 3 S-Odd MATH 3700 Elective MATH 3800 Partial Differential Equations 3 F-Odd MATH 2210 and 2250 or 2280 Credits (15 total Instructor Permissission; may repeat up MATH 3990 Undergraduate Research 1-3 *** credits to 5 cr. -

Axiomatic Foundations of Mathematics Ryan Melton Dr
Axiomatic Foundations of Mathematics Ryan Melton Dr. Clint Richardson, Faculty Advisor Stephen F. Austin State University As Bertrand Russell once said, Gödel's Method Pure mathematics is the subject in which we Consider the expression First, Gödel assigned a unique natural number to do not know what we are talking about, or each of the logical symbols and numbers. 2 + 3 = 5 whether what we are saying is true. Russell’s statement begs from us one major This expression is mathematical; it belongs to the field For example: if the symbol '0' corresponds to we call arithmetic and is composed of basic arithmetic question: the natural number 1, '+' to 2, and '=' to 3, then symbols. '0 = 0' '0 + 0 = 0' What is Mathematics founded on? On the other hand, the sentence and '2 + 3 = 5' is an arithmetical formula. 1 3 1 1 2 1 3 1 so each expression corresponds to a sequence. Axioms and Axiom Systems is metamathematical; it is constructed outside of mathematics and labels the expression above as a Then, for this new sequence x1x2x3…xn of formula in arithmetic. An axiom is a belief taken without proof, and positive integers, we associate a Gödel number thus an axiom system is a set of beliefs as follows: x1 x2 x3 xn taken without proof. enc( x1x2x3...xn ) = 2 3 5 ... pn Since Principia Mathematica was such a bold where the encoding is the product of n factors, Consistent? Complete? leap in the right direction--although proving each of which is found by raising the j-th prime nothing about consistency--several attempts at to the xj power. -

MATH S121 a Foundation in Pure Mathematics (Free Courseware) © the Open University of Hong Kong
MATH S121 A Foundation In Pure Mathematics (Free Courseware) © The Open University of Hong Kong This work is licensed under a Creative Commons-ShareAlike 4.0 International License Contents Chapter 1 Counting and Basic Probability ..................................................................1 1.1 About this module..............................................................................................................1 1.2 Introduction ........................................................................................................................2 1.3 Counting .............................................................................................................................2 1.3.1 Number of outcomes of an event .........................................................................2 1.3.2 Addition Principle ....................................................................................................3 1.3.3 Multiplication Principle ...........................................................................................4 1.3.4 Permutations and combinations...........................................................................6 1.3.4.1 Permutation..................................................................................................7 1.3.4.2 Activity 1 .......................................................................................................8 1.3.4.2.1 Activity 1 feedback ............................................................................8 1.3.4.3 Combinations ...............................................................................................8 -

The Foundations of Mathematics, in Accordance with the General Method of Frege, Whitehead, and Bussell
$88 F. P. KAMSEY [NOV. 12, THK FOUNDATIONS OF MATHEMATICS By F. P. KAMSEY. [Received 23 August, 1925.—Read 12 November, 1925.] Preface. THE object of this paper is to give a satisfactory account of the Foundations of Mathematics, in accordance with the general method of Frege, Whitehead, and Bussell. Following these authorities, I hold that mathematics is part of logic, and so belong to what may be called the logical school as opposed to the formalist and intuitionist schools. I have therefore taken Principia Mathematica as a basis for discussion and amendment, and believe myself to have discovered how, by using the work of Mr. Ludwig Wittgenstein, it can be rendered free from the serious objections which have caused its rejection by the majority of German authorities.who have deserted altogether its line of approach. Contents. I. Introduction. II. Principia Matliematica. III. Predicative Functions. IV. Functions in Extension. V. The Axioms. I. Introduction. In this chapter we shall be concerned with the general nature of pure mathematics*, and how it is distinguished from other sciences. • In future by "mathematics " will always be meant " pure mathematics." 1925.] THE FOUNDATIONS OF MATHEMATICS. 889 Here there are really two distinct categories of things of which an account must be given, the ideas or concepts of mathematics, and the propositions of mathematics. This distinction is neither artificial nor unnecessary, for the great majority of writers on the subject have con- centrated their attention on the explanation of one or other of these categories, and erroneously supposed that a satisfactory explanation of the other would immediately follow. -

Randomness in Arithmetic and the Decline and Fall of Reductionism in Pure Mathematics
RANDOMNESS IN ARITHMETIC AND THE DECLINE AND FALL OF REDUCTIONISM IN PURE MATHEMATICS IBM Research Report RC-18532 November 1992 arXiv:chao-dyn/9304002v1 7 Apr 1993 G. J. Chaitin Lecture given Thursday 22 October 1992 at a Mathematics – Computer Science Colloquium at the University of New Mexico. The lecture was videotaped; this is an edited transcript. 1. Hilbert on the axiomatic method Last month I was a speaker at a symposium on reductionism at Cam- bridge University where Turing did his work. I’d like to repeat the talk 1 2 I gave there and explain how my work continues and extends Turing’s. Two previous speakers had said bad things about David Hilbert. So I started by saying that in spite of what you might have heard in some of the previous lectures, Hilbert was not a twit! Hilbert’s idea is the culmination of two thousand years of math- ematical tradition going back to Euclid’s axiomatic treatment of ge- ometry, going back to Leibniz’s dream of a symbolic logic and Russell and Whitehead’s monumental Principia Mathematica. Hilbert’s dream was to once and for all clarify the methods of mathematical reasoning. Hilbert wanted to formulate a formal axiomatic system which would encompass all of mathematics. Formal Axiomatic System −→ −→ −→ Hilbert emphasized a number of key properties that such a formal axiomatic system should have. It’s like a computer programming lan- guage. It’s a precise statement about the methods of reasoning, the postulates and the methods of inference that we accept as mathemati- cians. -

History of Mathematics in the Higher Education Curriculum
History of Mathematics in the Higher Education Curriculum Mathematical Sciences HE Curriculum Innovation Project Innovation Curriculum HE Sciences Mathematical Edited by Mark McCartney History of Mathematics in the Higher Education Curriculum Edited by Mark McCartney A report by the working group on History of Mathematics in the Higher Education Curriculum, May 2012. Supported by the Maths, Stats and OR Network, as part of the Mathematical Sciences Strand of the National HE STEM Programme, and the British Society for the History of Mathematics (BSHM). Working group members: Noel-Ann Bradshaw (University of Greenwich; BSHM Treasurer); Snezana Lawrence (Bath Spa University; BSHM Education Officer); Mark McCartney (University of Ulster; BSHM Publicity Officer); Tony Mann (University of Greenwich; BSHM Immediate Past President); Robin Wilson (Pembroke College, Oxford; BSHM President). History of Mathematics in the Higher Education Curriculum Contents Contents Introduction 5 Teaching the history of mathematics at the University of St Andrews 9 History in the undergraduate mathematics curriculum – a case study from Greenwich 13 Teaching History of Mathematics at King’s College London 15 History for learning Analysis 19 History of Mathematics in a College of Education Context 23 Teaching the history of mathematics at the Open University 27 Suggested Resources 31 History of Mathematics in the Higher Education Curriculum Introduction Introduction Mathematics is usually, and of course correctly, presented ‘ready-made’ to students, with techniques and applications presented systematically and in logical order. However, like any other academic subject, mathematics has a history which is rich in astonishing breakthroughs, false starts, misattributions, confusions and dead-ends. This history gives a narrative and human context which adds colour and context to the discipline. -

Short Communication on Euclidean Geometry
Mathematica Eterna Short Communication 2021 Short Communication on Euclidean Geometry Joseph* Department of Mathematics, University of Patras, Greece The word “geometry” comes from the Greek words “geo”, elementary geometry. it had been through his works, we've got a which implies the “earth”, and “matron”, which implies “to collective supply for learning pure mathematics; it lays the measure”. Euclidean geometry could be a mathematical system inspiration for geometry as we all know currently. attributed to geometer an instructor of arithmetic in Alexandria Euclidean Axioms in Egypt. geometer gave North American nation associate exceptional plan concerning the fundamental ideas of pure Here square measure the seven axioms given by geometer for pure mathematics, in his book referred to as “Elements”. mathematics. 1. Things that square measure up to identical issue square Euclid listed twenty three definitions in his book “Elements”. measure up to each other. Some small print square measure mentioned below: 2. If equals square measure additional to equals, the wholes • A line is associate endless length. square measure equal. • A purpose has no dimension (length, breadth and width). 3. If equals square measure subtracted from equals, the • A line that lies equally with the points on itself could be a remainders square measure equal. line. 4. Things that coincide with each other square measure up to • Points square measure the ends of a line. each other. • A surface is that that has breadth and length solely. 5. The total is larger than the half. • A plane surface could be a surface that lies equally with the 6. Things that square measure double of identical things square straight lines on itself. -

On the Tension Between Physics and Mathematics∗
On the tension between physics and mathematics∗ Mikl´osR´edeiy Department of Philosophy, Logic and Scientific Method London School of Economics and Political Science Houghton Street London WC2A 2AE e-mail: [email protected] May 28, 2019 Abstract Because of the complex interdependence of physics and mathematics their relation is not free of tensions. The paper looks at how the tension has been perceived and articulated by some physicists, mathematicians and mathematical physicists. Some sources of the tension are identified and it is claimed that the tension is both natural and fruitful for both physics and mathematics. An attempt is made to explain why mathematical precision is typically not welcome in physics. 1 The "supermarket picture" of the relation of physics and mathematics, and Tension of type I According to what can be called the standard picture of the relation of physics and mathematics, physics is a science in the modern sense because it is systematically mathematical, which means two things: (a) Physics carries out precision measurements aiming at determining values of operationally defined physical quantities. This is what quantitative experimental physics does, and this ensures descriptive accuracy of physics. (b) Physics sets up mathematical models of physical phenomena that make explicit the func- tional relationships among the measured quantities; i.e. physics formulates general quan- titative physical laws. This is the main activity in theoretical physics and this enables physics to be predictively successful. Both descriptive accuracy and predictive success should be understood here with a number of qualifications: the descriptive accuracy is never perfect (experimental errors); the operationally defined quantities are not purely empirical (theory-ladenness of observations), natural laws may also refer to entities that are not observable strictly speaking, etc. -

Bertrand Russell – Principles of Mathematics
Principles of Mathematics “Unless we are very much mistaken, its lucid application and develop- ment of the great discoveries of Peano and Cantor mark the opening of a new epoch in both philosophical and mathematical thought” – The Spectator Bertrand Russell Principles of Mathematics London and New York First published in 1903 First published in the Routledge Classics in 2010 by Routledge 2 Park Square, Milton Park, Abingdon, Oxon OX14 4RN Routledge is an imprint of the Taylor & Francis Group, an informa business This edition published in the Taylor & Francis e-Library, 2009. To purchase your own copy of this or any of Taylor & Francis or Routledge’s collection of thousands of eBooks please go to www.eBookstore.tandf.co.uk. © 2010 The Bertrand Russell Peace Foundation Ltd Introduction © 1992 John G. Slater All rights reserved. No part of this book may be reprinted or reproduced or utilized in any form or by any electronic, mechanical, or other means, now known or hereafter invented, including photocopying and recording, or in any information storage or retrieval system, without permission in writing from the publishers. British Library Cataloguing in Publication Data A catalogue record for this book is available from the British Library Library of Congress Cataloging in Publication Data A catalog record for this book has been requested ISBN 0-203-86476-X Master e-book ISBN ISBN 10: 0-415-48741-2 ISBN 10: 0-203-86476-X (ebk) ISBN 13: 978-0-415-48741-2 ISBN 13: 978-0-203-86476-0 (ebk) CONTENTS introduction to the 1992 edition xxv introduction to the second edition xxxi preface xliii PART I THE INDEFINABLES OF MATHEMATICS 1 1 Definition of Pure Mathematics 3 1. -

Fig. III.2A. Gauss - Weber Collage According to an Idea of Friedrich Zöllner
Fig. III.2A. Gauss - Weber collage according to an idea of Friedrich Zöllner. Reproduced from [Zöllner 1878], page v, by courtesy of NSUB Göttingen. III.2 ‘O θo`ςαριθμητιζ´ ι — The Rise of Pure Mathematics as Arithmetic with Gauss JOSE´ FERREIROS1 The beautiful picture facing this page, which displays Carl Gauss and his colleague physicist Wilhelm Weber, is noteworthy not just for the quality and accuracy of the portraits, but also because of the mottos it includes. It was composed upon the inspiration of Friedrich Zöllner (1834–1882), an astrophysicist, professor at Berlin, and close follower of Weber.2 Among the mottos, one originates with Gauss himself: o θo`ςαριθμητιζ´ ι, God does arithmetic, or more literally “God arithmetizes” – presumably meaning that in his thoughts God is always dealing with numbers and number-relations. This motto is an adaptation of a sentence attributed to Plato: o θoςαιγωμτρι´ , “God geometrizes eternally.”3 Although this sentence is not found in Plato’s dialogues, nevertheless they offer declarations in the same spirit (see for instance the dialogue The Republic). Interestingly, the very same sentence, in Greek, is quoted by Kepler in his first work, Mysterium cosmographicum (1596), a book that Gauss must have been familiar with. Plato’s words can be found in the crucial chapter where Kepler describes the main guidelines of his peculiarly platonic 1. Universidad de Sevilla. I am grateful to participants in the Gauss Tagung at Oberwolfach for their reactions, and more particularly to Catherine Goldstein, Norbert Schappacher and Jeremy Gray for their criticism and suggestions based on a previous version of this paper.