DOCSLIB.ORG

2014 Eisenbud Prize for Mathematics and Physics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
2014 Eisenbud Prize for Mathematics and Physics 2014 Eisenbud Prize for Mathematics and Physics Gregory W. Moore was awarded Biographical Sketch the 2014 Leonard Eisenbud Prize Gregory W. Moore received his A.B. in physics from for Mathematics and Physics at the Princeton University in 1982 and his Ph.D. in phys- 120th Annual Meeting of the AMS in ics from Harvard University in 1985. He then joined Baltimore, Maryland, in January 2014. the Harvard Society of Fellows and in 1987 became a five-year member at the Institute for Advanced Citation Study (IAS) in Princeton. In 1989 he joined the The 2014 Leonard Eisenbud Prize for faculty at Yale University. He moved to the Depart- Mathematics and Physics is awarded ment of Physics and Astronomy at Rutgers Univer- to Gregory W. Moore for his group sity in 2000. He has held visiting professorships of works on the structure of four- at the Kalvi Institute for Theoretical Physics (KITP) Gregory W. Moore dimensional supersymmetric theories in Santa Barbara, California, and at the IAS. The with extended supersymmetry. His Inspire HEP database lists 170 papers coauthored works on supersymmetric solitons in a variety by Professor Moore on physical mathematics, with of contexts—including black holes in supergrav- an emphasis on geometrical structures in physics. ity, branes in string theory, and monopoles in Most notably he has worked on rational conformal gauge theory—have led to an explanation of the field theories (with applications to condensed mat- wall-crossing phenomena in the BPS spectrum. ter physics), two-dimensional quantum gravity and Moore’s research has injected new physical ideas matrix models, topological field theories, string and created new constructions in the mathematical dualities and D-branes, applications of K-theory to fields of cluster algebras, integrable systems, and string theory, connections between number theory hyperkähler geometry. and supersymmetric black holes, and the proper- In particular the following papers are cited: ties of BPS states of supersymmetric theories with 1. Frederik Denef and Gregory W. Moore, “Split an emphasis in recent years on their wall-crossing states, entropy enigmas, holes and halos”, Journal properties and relations to hyperkähler geometry. of High Energy Physics 129 (2011), no. 11, i, 152 pp. He is a member of the American Physical Society, 2. Duiliu-Emanuel Diaconescu and Gregory W. the American Mathematical Society, the American Moore, “Crossing the wall: branes versus bundles”, Academy of Arts and Sciences, and a general mem- Advances in Theoretical Mathematical Physics 14 ber of the Aspen Center for Physics. (2010), no. 6, 1621–1650. Response from Gregory W. Moore 3. Davide Gaiotto, Gregory W. Moore, and An- drew Neitzke, “Four-dimensional wall-crossing via I am deeply honored, and not a little surprised, to three-dimensional field theory”, Communications be the sole recipient of the 2014 Leonard Eisen- in Mathematical Physics 299 (2010), no. 1, 163–224. bud Prize for Mathematics and Physics. First and 4. Davide Gaiotto, Gregory W. Moore, and An- foremost I would like to thank my collaborators, drew Neitzke, “Wall-crossing, Hitchin systems, and Frederik Denef, Emanuel Diaconescu, Davide Gaiotto, and Andrew Neitzke, for their essential the WKB approximation,” Advances in Mathematics insights and enthusiasm for what turned out to 234 (2013), 239–403. be a very fruitful line of enquiry. I was the senior 5. Davide Gaiotto, Gregory W. Moore, and An- author only in years—not infrequently it was my drew Neitzke, “Spectral networks”, Annales Henri collaborators who were leading the charge. Poincaré 14 (2013), no. 7, 1643–1731. Since the AMS has requested a response to this DOI: http://dx.doi.org/10.1090/noti1113 award, I will use the opportunity to sketch my 406 NOTICES OF THE AMS VOLUME 61, NUMBER 4 viewpoint on how the work mentioned in the Kontsevich and Yan Soibelman and separately citation fits into a broader context and then to by Dominic Joyce and Yinan Song in their work conclude even more broadly with some thoughts on generalized Donaldson-Thomas invariants for on the place of physical mathematics in the con- Calabi-Yau categories. Research into BPS states temporary relation of the mathematical and physi- continues to be a very active subject. cal sciences. As indicated in the citation, the investigations A central theme of the work in the citation is the into the BPS spectrum have led to a wide variety of behavior of four-dimensional theories with N=2 unexpected and rich connections to many branches supersymmetry. The 1994 breakthrough of Nathan of pure mathematics. Like a beautiful flower Seiberg and Edward Witten amply demonstrated which continues to unfold and dazzle, the deeper that quantum field theories with extended super- the probe, the richer the emergent mathematics. symmetry constitute a Goldilocks class of theories In addition to the relations of four-dimensional which are special enough to admit exact nontrivial N=2 theories to hyperkähler geometry, cluster results on their dynamics but general enough to algebras, cluster varieties, and integrable systems, exhibit a host of nontrivial phenomena in quantum several other remarkable links to subjects in field theory. The promise of the Seiberg-Witten pure mathematics have been discovered by many breakthrough is twofold: First, one can make exact mathematicians and physicists in the past several statements about how the massless particles in the years. The full list is too long to mention here, but theory interact at low energies. Second, one can some prominent examples include deep relations make exact statements about the spectrum of the to geometric representation theory and nontrivial Hamiltonian for a subsector of the Hilbert space connections with modular tensor categories and of states called the “BPS subspace”. One of the key two-dimensional conformal field theory. features of these theories is that the vacuum state In view of the extraordinary richness of the field, is not unique, but rather it is parameterized by a one might well wonder if there is some simplifying manifold (which carries a special Kähler metric). and unifying viewpoint on all the above connec- Thus, an example of the first kind of result is an tions. Indeed, the following is widely believed by exact description of the strength of Coulomb’s law many mathematicians and physicists: A striking as a function of the vacuum parameters. prediction of string theory from the mid-1990s (in I would guesstimate that there have been well the hands of Edward Witten, Andrew Strominger, over ten thousand physicist years devoted to the and Nathan Seiberg) is that there is a class of intense investigation of four-dimensional N =2 six-dimensional interacting conformal quantum field theories. Nevertheless, the full promise of field theories known as the (2,0)-theories. Many the Seiberg-Witten breakthrough has not yet been of the beautiful connections alluded to above can fully realized. Regarding the first kind of result, be traced to the very existence of these theories. important and nontrivial insights continue to be On the other hand, these six-dimensional theories uncovered up to the present day in the works of have not yet been fully formulated in any system- Nikita Nekrasov, Samson Shatashvili, Vasily Pes- atic way. There is no analog of a statement for tun, Edward Witten, and a host of others revealing nonabelian gauge theory, such as “Make sense of relations to integrable systems and many other the path integral over connections on a principal things. The papers mentioned in the citation ad- bundle weighted by the Yang-Mills action.” Indeed dress the second kind of result: deepening our the very mention of the (2,0)-theories is greeted by understanding of how to compute the so-called BPS some scientists with an indulgent smile. But many spectrum for ever larger classes of N =2 theories. of us take them seriously. An important problem The key theme in these papers is that, as a func- for the future is a deeper understanding and for- tion of vacuum parameters, the BPS spectrum can mulation of these theories. be discontinuous across real codimension 1 loci For reviews giving a more extensive explana- in the space of vacuum parameters. An important tion of these matters, the reader could consult my point is that there exists a very beautiful formula review talk at Strings2011 in Uppsala, Sweden, my which expresses how this spectrum changes. Since review talk at the 2012 International Congress on a real codimension 1 locus is a wall, the formula Mathematics and Physics in Aalborg, Denmark, or is known as a wall-crossing formula. The history my 2012 Felix Klein lectures delivered in Bonn, of this formula is far too complicated to be ex- Germany. They are all available on my home page. plained here, but I will note that it began with a I would like to stress that there are several view- formula of Sergio Cecotti and Cumrun Vafa for the points on this vibrant subject held by several other decays of solitons in two-dimensional quantum mathematicians and physicists which are equally if field theories, and, in addition to my work done not more valid. For a good example, see the review in collaboration with Denef, Diaconescu, Gaiotto, by Yuji Tachikawa, available on his home page. and Neitzke, essential insights and breakthroughs Looking further to the future, we should not were made in the context of pure mathematics— forget that the very existence of the (2,0)-theory and motivated by pure mathematics—by Maxim is but a corollary of the existence of string theory. APRIL 2014 NOTICES OF THE AMS 407 Work on the fundamental principles underlying the AMS during 2003–2004. The Eisenbud Prize for string theory has noticeably waned—it seems the Mathematics and Physics honors a work or group community is currently gathering more “data” of works that brings the two fields closer together.
Load more

Recommended publications
  • Stephen Hawking (1942–2018) World-Renowned Physicist Who Defied the Odds
    COMMENT OBITUARY Stephen Hawking (1942–2018) World-renowned physicist who defied the odds. hen Stephen Hawking was speech synthesizer processed his words and diagnosed with motor-neuron generated the androidal accent that became disease at the age of 21, it wasn’t his trademark. In this way, he completed his Wclear that he would finish his PhD. Against best-selling book A Brief History of Time all expectations, he lived on for 55 years, (Bantam, 1988), which propelled him to becoming one of the world’s most celebrated celebrity status. IAN BERRY/MAGNUM scientists. Had Hawking achieved equal distinction Hawking, who died on 14 March 2018, was in any other branch of science besides cos- born in Oxford, UK, in 1942 to a medical- mology, it probably would not have had the researcher father and a philosophy-graduate same resonance with a worldwide public. As mother. After attending St Albans School I put it in The Telegraph newspaper in 2007, near London, he earned a first-class degree “the concept of an imprisoned mind roaming in physics from the University of Oxford. He the cosmos” grabbed people’s imagination. began his research career in 1962, enrolling In 1965, Stephen married Jane Wilde. as a graduate student in a group at the Uni- After 25 years of marriage, and three versity of Cambridge led by one of the fathers children, the strain of Stephen’s illness of modern cosmology, Dennis Sciama. and of sharing their home with a team of The general theory of relativity was at that nurses became too much and they sepa- time undergoing a renaissance, initiated in rated, divorcing in 1995.
    [Show full text]
  • CERN Celebrates Discoveries
    INTERNATIONAL JOURNAL OF HIGH-ENERGY PHYSICS CERN COURIER VOLUME 43 NUMBER 10 DECEMBER 2003 CERN celebrates discoveries NEW PARTICLES NETWORKS SPAIN Protons make pentaquarks p5 Measuring the digital divide pl7 Particle physics thrives p30 16 KPH impact 113 KPH impact series VISyN High Voltage Power Supplies When the objective is to measure the almost immeasurable, the VISyN-Series is the detector power supply of choice. These multi-output, card based high voltage power supplies are stable, predictable, and versatile. VISyN is now manufactured by Universal High Voltage, a world leader in high voltage power supplies, whose products are in use in every national laboratory. For worldwide sales and service, contact the VISyN product group at Universal High Voltage. Universal High Voltage Your High Voltage Power Partner 57 Commerce Drive, Brookfield CT 06804 USA « (203) 740-8555 • Fax (203) 740-9555 www.universalhv.com Covering current developments in high- energy physics and related fields worldwide CERN Courier (ISSN 0304-288X) is distributed to member state governments, institutes and laboratories affiliated with CERN, and to their personnel. It is published monthly, except for January and August, in English and French editions. The views expressed are CERN not necessarily those of the CERN management. Editor Christine Sutton CERN, 1211 Geneva 23, Switzerland E-mail: [email protected] Fax:+41 (22) 782 1906 Web: cerncourier.com COURIER Advisory Board R Landua (Chairman), P Sphicas, K Potter, E Lillest0l, C Detraz, H Hoffmann, R Bailey
    [Show full text]
  • Inflation, Large Branes, and the Shape of Space
    Inflation, Large Branes, and the Shape of Space Brett McInnes National University of Singapore email: [email protected] ABSTRACT Linde has recently argued that compact flat or negatively curved spatial sections should, in many circumstances, be considered typical in Inflationary cosmologies. We suggest that the “large brane instability” of Seiberg and Witten eliminates the negative candidates in the context of string theory. That leaves the flat, compact, three-dimensional manifolds — Conway’s platycosms. We show that deep theorems of Schoen, Yau, Gromov and Lawson imply that, even in this case, Seiberg-Witten instability can be avoided only with difficulty. Using a specific cosmological model of the Maldacena-Maoz type, we explain how to do this, and we also show how the list of platycosmic candidates can be reduced to three. This leads to an extension of the basic idea: the conformal compactification of the entire Euclidean spacetime also has the topology of a flat, compact, four-dimensional space. arXiv:hep-th/0410115v2 19 Oct 2004 1. Nearly Flat or Really Flat? Linde has recently argued [1] that, at least in some circumstances, we should regard cosmological models with flat or negatively curved compact spatial sections as the norm from an Inflationary point of view. Here we wish to argue that cosmic holography, in the novel form proposed by Maldacena and Maoz [2], gives a deep new interpretation of this idea, and also sharpens it very considerably to exclude the negative case. This focuses our attention on cosmological models with flat, compact spatial sections. Current observations [3] show that the spatial sections of our Universe [as defined by observers for whom local isotropy obtains] are fairly close to being flat: the total density parameter Ω satisfies Ω = 1.02 0.02 at 95% confidence level, if we allow the imposition ± of a reasonable prior [4] on the Hubble parameter.
    [Show full text]
  • Christopher Elliott
    Christopher Elliott Contact Details Full Name Christopher James Elliott Date of Birth 20th Sep, 1987 Nationality British Contact Address University of Massachusetts Department of Mathematics and Statistics 710 N Pleasant St Amherst, MA 01003 USA E-mail Address [email protected] Work Experience 2019– Visiting Assistant Professor, University of Massachusetts, Amherst 2016–2019 Postdoctoral Fellow, Institut des Hautes Etudes´ Scientifiques Education 2010–2016 PhD, Northwestern University Advisors: Kevin Costello and David Nadler Thesis Title: Gauge Theoretic Aspects of the Geometric Langlands Correspondence. 2009–2010 MMath (Mathematics Tripos: Part III), University of Cambridge, With Distinction. Part III Essay: D-Modules and Hodge Theory 2006–2009 BA (hons) (Mathematics), University of Cambridge, 1st Class. Research Visits 2014–2018 Perimeter Institute (7 visits, each 1-3 weeks) Oct–Nov 2017 MPIM, Bonn Oct 2017 Hausdorff Institute, Bonn Nov 2016 MPIM, Bonn Research Interests I’m interested in mathematical aspects and applications of quantum field theory. In particular • The construction and classification of (not necessarily topological) twists of classical and quantum field theories, especially using techniques of derived algebraic geometry and homotopical algebra. • The connection between structures appearing in various versions of the geometric Langlands correspon- dence and twists of four-, five- and six-dimensional supersymmetric gauge theories. • The theory of factorization algebras as a model for perturbative quantum field theory, possibly with bound- ary conditions and defects. Publications and Preprints 1. Quantum Geometric Langlands Categories from N = 4 Super Yang–Mills Theory (joint with Philsang Yoo), arXiv:2008.10988 2. Spontaneous Symmetry Breaking: a View from Derived Geometry (joint with Owen Gwilliam), Journal of Geometry and Physics, Vol 162, 2021, arXiv:2008.02302 1 3.
    [Show full text]
  • Anomalies, Dualities, and Topology of D = 6 N = 1 Superstring Vacua
    RU-96-16 NSF-ITP-96-21 CALT-68-2057 IASSNS-HEP-96/53 hep-th/9605184 Anomalies, Dualities, and Topology of D =6 N =1 Superstring Vacua Micha Berkooz,1 Robert G. Leigh,1 Joseph Polchinski,2 John H. Schwarz,3 Nathan Seiberg,1 and Edward Witten4 1Department of Physics, Rutgers University, Piscataway, NJ 08855-0849 2Institute for Theoretical Physics, University of California, Santa Barbara, CA 93106-4030 3California Institute of Technology, Pasadena, CA 91125 4Institute for Advanced Study, Princeton, NJ 08540 Abstract We consider various aspects of compactifications of the Type I/heterotic Spin(32)/Z2 theory on K3. One family of such compactifications in- cludes the standard embedding of the spin connection in the gauge group, and is on the same moduli space as the compactification of arXiv:hep-th/9605184v1 25 May 1996 the heterotic E8 × E8 theory on K3 with instanton numbers (8,16). Another class, which includes an orbifold of the Type I theory re- cently constructed by Gimon and Polchinski and whose field theory limit involves some topological novelties, is on the moduli space of the heterotic E8 × E8 theory on K3 with instanton numbers (12,12). These connections between Spin(32)/Z2 and E8 × E8 models can be demonstrated by T duality, and permit a better understanding of non- perturbative gauge fields in the (12,12) model. In the transformation between Spin(32)/Z2 and E8 × E8 models, the strong/weak coupling duality of the (12,12) E8 × E8 model is mapped to T duality in the Type I theory. The gauge and gravitational anomalies in the Type I theory are canceled by an extension of the Green-Schwarz mechanism.
    [Show full text]
  • Pure Mathematics Professors Teaching and Leading Research CO-OP OR REGULAR 28
    PURE MATHEMATICS Pure Mathematics professors teaching and leading research CO-OP OR REGULAR 28 Mathematician ranked among top 10 TOP 10 jobs from 2011-2017 – Comcast.com of grads are employed Search for a deeper 96.6% within 2 years understanding of mathematics Pure mathematics is at the foundation of all mathematical reasoning. If first-year calculus ALEX teaches you how to drive the car, Pure Mathematics teaches you how to build one. 3B, PURE MATHEMATICS AND Mathematicians know that there could be no general relativity without differential COMBINATORICS AND geometry, and no computer security without advanced number theory. OPTIMIZATION Pure Mathematics at Waterloo is a small, cohesive, and challenging program that will open countless doors for you. Our graduates have used the program as a springboard into careers WHAT DO YOU LOVE ABOUT in information technology, finance, business, science, education, and insurance, often by way PURE MATHEMATICS? The satisfaction from understanding of some of the most prestigious graduate programs in the world. an idea at a deeper level and tying together unrelated branches of ALEX’S FAVOURITE COURSES mathematics or physics for the › PMATH 320 Euclidean Geometry: This course is everything you love about Geometry: first time is the most rewarding Euclid’s axioms, isometries of the Euclidean plane and of Euclidean space, polygons, part of learning and understanding polyhedral, polytopes, and the kissing problem. mathematics. What I really enjoy is › PMATH 351 Real Analysis: It’s a very intuitive and natural approach to real analysis, and the developing a deep understanding of complexity of the course builds very naturally to the end of the semester.
    [Show full text]
  • Doing Physics with Math ...And Vice Versa
    Doing physics with math ...and vice versa Alexander Tabler Thessaloniki, December 19, 2019 Thessaloniki, December 19, 2019 0 / 14 Outline 1 Physics vs. Mathematics 2 Case study: a question about shapes 3 Enter physics & quantum field theory 4 Summary Thessaloniki, December 19, 2019 1 / 14 1. Physics vs. Mathematics Thessaloniki, December 19, 2019 1 / 14 Common origins, divergent futures At some point, Mathematics and Physics were the same discipline: Natural philosophy. Calculus: mathematics or physics? \Isaac Newton" - Godfrey Kneller - commons.curid=37337 Thessaloniki, December 19, 2019 2 / 14 Today, Math=Physics6 Mathematics: - Definition. Theorem. Proof. (Bourbaki-style mathematics) - Logical rigor, \waterproof" - \Proof"-driven (Theoretical) Physics: - Less rigor - Computation-oriented (\shut up and calculate") - Experiment-driven ...in principle Thessaloniki, December 19, 2019 3 / 14 An early 20th century divorce Freeman Dyson, 1972: \The marriage between mathematics and physics has recently ended in divorce"1 F. Dyson - by ioerror - commons.curid=71877726 1 Dyson - \Missed Opportunities", Bull. Amer. Math. Soc., Volume 78, Number 5 (1972), 635-652. Thessaloniki, December 19, 2019 4 / 14 A fruitful relation However, strong bonds still remain: - Modern theoretical physics uses more abstract mathematics - There is a deep relationship between advances in both fields - This relationship is mutually beneficial https://www.ias.edu/ideas/power-mirror-symmetry Thessaloniki, December 19, 2019 5 / 14 2. Case study: a question about shapes Thessaloniki,
    [Show full text]
  • String Theory for Pedestrians
    String Theory for Pedestrians Johanna Knapp ITP, TU Wien Atominstitut, March 4, 2016 Outline Fundamental Interactions What is String Theory? Modern String Theory String Phenomenology Gauge/Gravity Duality Physical Mathematics Conclusions Fundamental Interactions What is String Theory? Modern String Theory Conclusions Fundamental Interactions • Four fundamental forces of nature • Electromagnetic Interactions: Photons • Strong Interactions: Gluons • Weak Interactions: W- and Z-bosons • Gravity: Graviton (?) • Successful theoretical models • Quantum Field Theory • Einstein Gravity • Tested by high-precision experiments Fundamental Interactions What is String Theory? Modern String Theory Conclusions Gravity • General Relativity 1 R − g R = 8πGT µν 2 µν µν • Matter $ Curvature of spacetime • No Quantum Theory of Gravity! • Black Holes • Big Bang Fundamental Interactions What is String Theory? Modern String Theory Conclusions Particle Interactions • Strong, weak and electromagnetic interactions can be described by the Standard Model of Particle Physics • Quantum Field Theory • Gauge Theory Fundamental Interactions What is String Theory? Modern String Theory Conclusions Unification of Forces • Can we find a unified quantum theory of all fundamental interactions? • Reconciliation of two different theoretical frameworks • Quantum Theory of Gravity • Why is unification a good idea? • It worked before: electromagnetism, electroweak interactions • Evidence of unification of gauge couplings • Open problems of fundamental physics should be solved. Fundamental Interactions What is String Theory? Modern String Theory Conclusions History of the Universe • Physics of the early universe Fundamental Interactions What is String Theory? Modern String Theory Conclusions Energy Budget of the Universe • Only about 5% of the matter in the universe is understood. • What is dark matter? Extra particles? Fundamental Interactions What is String Theory? Modern String Theory Conclusions String Theory Fact Sheet • String theory is a quantum theory that unifies the fundamental forces of nature.
    [Show full text]
  • Supergravity at 40: Reflections and Perspectives(∗)
    RIVISTA DEL NUOVO CIMENTO Vol. 40, N. 6 2017 DOI 10.1393/ncr/i2017-10136-6 ∗ Supergravity at 40: Reflections and perspectives( ) S. Ferrara(1)(2)(3)andA. Sagnotti(4) (1) Theoretical Physics Department, CERN CH - 1211 Geneva 23, Switzerland (2) INFN - Laboratori Nazionali di Frascati - Via Enrico Fermi 40 I-00044 Frascati (RM), Italy (3) Department of Physics and Astronomy, Mani L. Bhaumik Institute for Theoretical Physics U.C.L.A., Los Angeles CA 90095-1547, USA (4) Scuola Normale Superiore e INFN - Piazza dei Cavalieri 7, I-56126 Pisa, Italy received 15 February 2017 Dedicated to John H. Schwarz on the occasion of his 75th birthday Summary. — The fortieth anniversary of the original construction of Supergravity provides an opportunity to combine some reminiscences of its early days with an assessment of its impact on the quest for a quantum theory of gravity. 280 1. Introduction 280 2. The early times 282 3. The golden age 283 4. Supergravity and particle physics 284 5. Supergravity and string theory 286 6. Branes and M-theory 287 7. Supergravity and the AdS/CFT correspondence 288 8. Conclusions and perspectives ∗ ( ) Based in part on the talk delivered by S.F. at the “Special Session of the DISCRETE2016 Symposium and the Leopold Infeld Colloquium”, in Warsaw, on December 1 2016, and on a joint CERN Courier article. c Societ`a Italiana di Fisica 279 280 S. FERRARA and A. SAGNOTTI 1. – Introduction The year 2016 marked the fortieth anniversary of the discovery of Supergravity (SGR) [1], an extension of Einstein’s General Relativity [2] (GR) where Supersymme- try, promoted to a gauge symmetry, accompanies general coordinate transformations.
    [Show full text]
  • Pure Mathematics
    Why Study Mathematics? Mathematics reveals hidden patterns that help us understand the world around us. Now much more than arithmetic and geometry, mathematics today is a diverse discipline that deals with data, measurements, and observations from science; with inference, deduction, and proof; and with mathematical models of natural phenomena, of human behavior, and social systems. The process of "doing" mathematics is far more than just calculation or deduction; it involves observation of patterns, testing of conjectures, and estimation of results. As a practical matter, mathematics is a science of pattern and order. Its domain is not molecules or cells, but numbers, chance, form, algorithms, and change. As a science of abstract objects, mathematics relies on logic rather than on observation as its standard of truth, yet employs observation, simulation, and even experimentation as means of discovering truth. The special role of mathematics in education is a consequence of its universal applicability. The results of mathematics--theorems and theories--are both significant and useful; the best results are also elegant and deep. Through its theorems, mathematics offers science both a foundation of truth and a standard of certainty. In addition to theorems and theories, mathematics offers distinctive modes of thought which are both versatile and powerful, including modeling, abstraction, optimization, logical analysis, inference from data, and use of symbols. Mathematics, as a major intellectual tradition, is a subject appreciated as much for its beauty as for its power. The enduring qualities of such abstract concepts as symmetry, proof, and change have been developed through 3,000 years of intellectual effort. Like language, religion, and music, mathematics is a universal part of human culture.
    [Show full text]
  • Some Comments on Physical Mathematics
    Preprint typeset in JHEP style - HYPER VERSION Some Comments on Physical Mathematics Gregory W. Moore Abstract: These are some thoughts that accompany a talk delivered at the APS Savannah meeting, April 5, 2014. I have serious doubts about whether I deserve to be awarded the 2014 Heineman Prize. Nevertheless, I thank the APS and the selection committee for their recognition of the work I have been involved in, as well as the Heineman Foundation for its continued support of Mathematical Physics. Above all, I thank my many excellent collaborators and teachers for making possible my participation in some very rewarding scientific research. 1 I have been asked to give a talk in this prize session, and so I will use the occasion to say a few words about Mathematical Physics, and its relation to the sub-discipline of Physical Mathematics. I will also comment on how some of the work mentioned in the citation illuminates this emergent field. I will begin by framing the remarks in a much broader historical and philosophical context. I hasten to add that I am neither a historian nor a philosopher of science, as will become immediately obvious to any expert, but my impression is that if we look back to the modern era of science then major figures such as Galileo, Kepler, Leibniz, and New- ton were neither physicists nor mathematicans. Rather they were Natural Philosophers. Even around the turn of the 19th century the same could still be said of Bernoulli, Euler, Lagrange, and Hamilton. But a real divide between Mathematics and Physics began to open up in the 19th century.
    [Show full text]
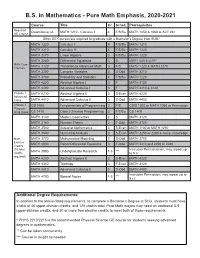
  • B.S. in Mathematics - Pure Math Emphasis, 2020-2021
    B.S. in Mathematics - Pure Math Emphasis, 2020-2021 Course Title Cr. Sched. Prerequisites Required Quantitative Lit. MATH 1210 - Calculus I 4 F/S/Su MATH 1050 & 1060 or ACT 26+ GE Course Other GE Courses are required to graduate with a Bachelor’s Degree from SUU.* MATH 1220 Calculus II 4 F/S/Su MATH 1210 MATH 2210 Calculus III 4 F/S/Su MATH 1220 MATH 2270 Linear Algebra 3 F/S/Su MATH 1220 MATH 2280 Differential Equations 3 S MATH 1220 & 2270** Math Core MATH 3120 Transition to Advanced Math 3 F/S MATH 1220 & MATH 2270 Courses MATH 3250 Complex Variables 3 S-Odd MATH 2210 MATH 3700 Probability and Statistics 4 F/S/Su MATH 1220 MATH 4220 Abstract Algebra I 3 F MATH 3120 MATH 4400 Advanced Calculus I 3 F MATH 2210 & 3120 Choose 1 MATH 4230 Abstract Algebra II 3 S-Even MATH 4220 Advanced Class MATH 4410 Advanced Calculus II 3 S-Odd MATH 4400 Choose 1 CS 1400 Fundamentals of Programming 3 F/S CSIS 1030 or MATH 1050 or Permission Program- ming Class CS 1410 Object Oriented Programming 3 F/S/Su CS 1400 MATH 3130 Modern Geometries 3 S MATH 3120 MATH 3160 Number Theory 3 F-Odd MATH 3120 MATH 3500 Actuarial Mathematics 3 S-Even MATH 1100 or MATH 1210 MATH 3600 Numerical Analysis 3 S-Even MATH 2250 or 2280 & comp. knowledge Math MATH 3770 Mathematical Modeling 3 S-Odd MATH 3700 Elective MATH 3800 Partial Differential Equations 3 F-Odd MATH 2210 and 2250 or 2280 Credits (15 total Instructor Permissission; may repeat up MATH 3990 Undergraduate Research 1-3 *** credits to 5 cr.
    [Show full text]