On the Tension Between Physics and Mathematics∗
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Research Statement
D. A. Williams II June 2021 Research Statement I am an algebraist with expertise in the areas of representation theory of Lie superalgebras, associative superalgebras, and algebraic objects related to mathematical physics. As a post- doctoral fellow, I have extended my research to include topics in enumerative and algebraic combinatorics. My research is collaborative, and I welcome collaboration in familiar areas and in newer undertakings. The referenced open problems here, their subproblems, and other ideas in mind are suitable for undergraduate projects and theses, doctoral proposals, or scholarly contributions to academic journals. In what follows, I provide a technical description of the motivation and history of my work in Lie superalgebras and super representation theory. This is then followed by a description of the work I am currently supervising and mentoring, in combinatorics, as I serve as the Postdoctoral Research Advisor for the Mathematical Sciences Research Institute's Undergraduate Program 2021. 1 Super Representation Theory 1.1 History 1.1.1 Superalgebras In 1941, Whitehead dened a product on the graded homotopy groups of a pointed topological space, the rst non-trivial example of a Lie superalgebra. Whitehead's work in algebraic topol- ogy [Whi41] was known to mathematicians who dened new graded geo-algebraic structures, such as -graded algebras, or superalgebras to physicists, and their modules. A Lie superalge- Z2 bra would come to be a -graded vector space, even (respectively, odd) elements g = g0 ⊕ g1 Z2 found in (respectively, ), with a parity-respecting bilinear multiplication termed the Lie g0 g1 superbracket inducing1 a symmetric intertwining map of -modules. -

Mathematical Methods of Classical Mechanics-Arnold V.I..Djvu
V.I. Arnold Mathematical Methods of Classical Mechanics Second Edition Translated by K. Vogtmann and A. Weinstein With 269 Illustrations Springer-Verlag New York Berlin Heidelberg London Paris Tokyo Hong Kong Barcelona Budapest V. I. Arnold K. Vogtmann A. Weinstein Department of Department of Department of Mathematics Mathematics Mathematics Steklov Mathematical Cornell University University of California Institute Ithaca, NY 14853 at Berkeley Russian Academy of U.S.A. Berkeley, CA 94720 Sciences U.S.A. Moscow 117966 GSP-1 Russia Editorial Board J. H. Ewing F. W. Gehring P.R. Halmos Department of Department of Department of Mathematics Mathematics Mathematics Indiana University University of Michigan Santa Clara University Bloomington, IN 47405 Ann Arbor, MI 48109 Santa Clara, CA 95053 U.S.A. U.S.A. U.S.A. Mathematics Subject Classifications (1991): 70HXX, 70005, 58-XX Library of Congress Cataloging-in-Publication Data Amol 'd, V.I. (Vladimir Igorevich), 1937- [Matematicheskie melody klassicheskoi mekhaniki. English] Mathematical methods of classical mechanics I V.I. Amol 'd; translated by K. Vogtmann and A. Weinstein.-2nd ed. p. cm.-(Graduate texts in mathematics ; 60) Translation of: Mathematicheskie metody klassicheskoi mekhaniki. Bibliography: p. Includes index. ISBN 0-387-96890-3 I. Mechanics, Analytic. I. Title. II. Series. QA805.A6813 1989 531 '.01 '515-dcl9 88-39823 Title of the Russian Original Edition: M atematicheskie metody klassicheskoi mekhaniki. Nauka, Moscow, 1974. Printed on acid-free paper © 1978, 1989 by Springer-Verlag New York Inc. All rights reserved. This work may not be translated or copied in whole or in part without the written permission of the publisher (Springer-Verlag, 175 Fifth Avenue, New York, NY 10010, U.S.A.), except for brief excerpts in connection with reviews or scholarly analysis. -

Pure Mathematics Professors Teaching and Leading Research CO-OP OR REGULAR 28
PURE MATHEMATICS Pure Mathematics professors teaching and leading research CO-OP OR REGULAR 28 Mathematician ranked among top 10 TOP 10 jobs from 2011-2017 – Comcast.com of grads are employed Search for a deeper 96.6% within 2 years understanding of mathematics Pure mathematics is at the foundation of all mathematical reasoning. If first-year calculus ALEX teaches you how to drive the car, Pure Mathematics teaches you how to build one. 3B, PURE MATHEMATICS AND Mathematicians know that there could be no general relativity without differential COMBINATORICS AND geometry, and no computer security without advanced number theory. OPTIMIZATION Pure Mathematics at Waterloo is a small, cohesive, and challenging program that will open countless doors for you. Our graduates have used the program as a springboard into careers WHAT DO YOU LOVE ABOUT in information technology, finance, business, science, education, and insurance, often by way PURE MATHEMATICS? The satisfaction from understanding of some of the most prestigious graduate programs in the world. an idea at a deeper level and tying together unrelated branches of ALEX’S FAVOURITE COURSES mathematics or physics for the › PMATH 320 Euclidean Geometry: This course is everything you love about Geometry: first time is the most rewarding Euclid’s axioms, isometries of the Euclidean plane and of Euclidean space, polygons, part of learning and understanding polyhedral, polytopes, and the kissing problem. mathematics. What I really enjoy is › PMATH 351 Real Analysis: It’s a very intuitive and natural approach to real analysis, and the developing a deep understanding of complexity of the course builds very naturally to the end of the semester. -

Mathematical Foundations of Supersymmetry
MATHEMATICAL FOUNDATIONS OF SUPERSYMMETRY Lauren Caston and Rita Fioresi 1 Dipartimento di Matematica, Universit`adi Bologna Piazza di Porta S. Donato, 5 40126 Bologna, Italia e-mail: [email protected], fi[email protected] 1Investigation supported by the University of Bologna 1 Introduction Supersymmetry (SUSY) is the machinery mathematicians and physicists have developed to treat two types of elementary particles, bosons and fermions, on the same footing. Supergeometry is the geometric basis for supersymmetry; it was first discovered and studied by physicists Wess, Zumino [25], Salam and Strathde [20] (among others) in the early 1970’s. Today supergeometry plays an important role in high energy physics. The objects in super geometry generalize the concept of smooth manifolds and algebraic schemes to include anticommuting coordinates. As a result, we employ the techniques from algebraic geometry to study such objects, namely A. Grothendiek’s theory of schemes. Fermions include all of the material world; they are the building blocks of atoms. Fermions do not like each other. This is in essence the Pauli exclusion principle which states that two electrons cannot occupy the same quantum me- chanical state at the same time. Bosons, on the other hand, can occupy the same state at the same time. Instead of looking at equations which just describe either bosons or fermions separately, supersymmetry seeks out a description of both simultaneously. Tran- sitions between fermions and bosons require that we allow transformations be- tween the commuting and anticommuting coordinates. Such transitions are called supersymmetries. In classical Minkowski space, physicists classify elementary particles by their mass and spin. -

Pure Mathematics
Why Study Mathematics? Mathematics reveals hidden patterns that help us understand the world around us. Now much more than arithmetic and geometry, mathematics today is a diverse discipline that deals with data, measurements, and observations from science; with inference, deduction, and proof; and with mathematical models of natural phenomena, of human behavior, and social systems. The process of "doing" mathematics is far more than just calculation or deduction; it involves observation of patterns, testing of conjectures, and estimation of results. As a practical matter, mathematics is a science of pattern and order. Its domain is not molecules or cells, but numbers, chance, form, algorithms, and change. As a science of abstract objects, mathematics relies on logic rather than on observation as its standard of truth, yet employs observation, simulation, and even experimentation as means of discovering truth. The special role of mathematics in education is a consequence of its universal applicability. The results of mathematics--theorems and theories--are both significant and useful; the best results are also elegant and deep. Through its theorems, mathematics offers science both a foundation of truth and a standard of certainty. In addition to theorems and theories, mathematics offers distinctive modes of thought which are both versatile and powerful, including modeling, abstraction, optimization, logical analysis, inference from data, and use of symbols. Mathematics, as a major intellectual tradition, is a subject appreciated as much for its beauty as for its power. The enduring qualities of such abstract concepts as symmetry, proof, and change have been developed through 3,000 years of intellectual effort. Like language, religion, and music, mathematics is a universal part of human culture. -

Renormalization and Effective Field Theory
Mathematical Surveys and Monographs Volume 170 Renormalization and Effective Field Theory Kevin Costello American Mathematical Society surv-170-costello-cov.indd 1 1/28/11 8:15 AM http://dx.doi.org/10.1090/surv/170 Renormalization and Effective Field Theory Mathematical Surveys and Monographs Volume 170 Renormalization and Effective Field Theory Kevin Costello American Mathematical Society Providence, Rhode Island EDITORIAL COMMITTEE Ralph L. Cohen, Chair MichaelA.Singer Eric M. Friedlander Benjamin Sudakov MichaelI.Weinstein 2010 Mathematics Subject Classification. Primary 81T13, 81T15, 81T17, 81T18, 81T20, 81T70. The author was partially supported by NSF grant 0706954 and an Alfred P. Sloan Fellowship. For additional information and updates on this book, visit www.ams.org/bookpages/surv-170 Library of Congress Cataloging-in-Publication Data Costello, Kevin. Renormalization and effective fieldtheory/KevinCostello. p. cm. — (Mathematical surveys and monographs ; v. 170) Includes bibliographical references. ISBN 978-0-8218-5288-0 (alk. paper) 1. Renormalization (Physics) 2. Quantum field theory. I. Title. QC174.17.R46C67 2011 530.143—dc22 2010047463 Copying and reprinting. Individual readers of this publication, and nonprofit libraries acting for them, are permitted to make fair use of the material, such as to copy a chapter for use in teaching or research. Permission is granted to quote brief passages from this publication in reviews, provided the customary acknowledgment of the source is given. Republication, systematic copying, or multiple reproduction of any material in this publication is permitted only under license from the American Mathematical Society. Requests for such permission should be addressed to the Acquisitions Department, American Mathematical Society, 201 Charles Street, Providence, Rhode Island 02904-2294 USA. -
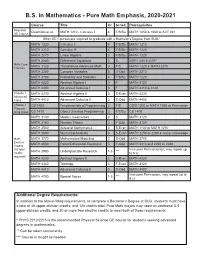
B.S. in Mathematics - Pure Math Emphasis, 2020-2021
B.S. in Mathematics - Pure Math Emphasis, 2020-2021 Course Title Cr. Sched. Prerequisites Required Quantitative Lit. MATH 1210 - Calculus I 4 F/S/Su MATH 1050 & 1060 or ACT 26+ GE Course Other GE Courses are required to graduate with a Bachelor’s Degree from SUU.* MATH 1220 Calculus II 4 F/S/Su MATH 1210 MATH 2210 Calculus III 4 F/S/Su MATH 1220 MATH 2270 Linear Algebra 3 F/S/Su MATH 1220 MATH 2280 Differential Equations 3 S MATH 1220 & 2270** Math Core MATH 3120 Transition to Advanced Math 3 F/S MATH 1220 & MATH 2270 Courses MATH 3250 Complex Variables 3 S-Odd MATH 2210 MATH 3700 Probability and Statistics 4 F/S/Su MATH 1220 MATH 4220 Abstract Algebra I 3 F MATH 3120 MATH 4400 Advanced Calculus I 3 F MATH 2210 & 3120 Choose 1 MATH 4230 Abstract Algebra II 3 S-Even MATH 4220 Advanced Class MATH 4410 Advanced Calculus II 3 S-Odd MATH 4400 Choose 1 CS 1400 Fundamentals of Programming 3 F/S CSIS 1030 or MATH 1050 or Permission Program- ming Class CS 1410 Object Oriented Programming 3 F/S/Su CS 1400 MATH 3130 Modern Geometries 3 S MATH 3120 MATH 3160 Number Theory 3 F-Odd MATH 3120 MATH 3500 Actuarial Mathematics 3 S-Even MATH 1100 or MATH 1210 MATH 3600 Numerical Analysis 3 S-Even MATH 2250 or 2280 & comp. knowledge Math MATH 3770 Mathematical Modeling 3 S-Odd MATH 3700 Elective MATH 3800 Partial Differential Equations 3 F-Odd MATH 2210 and 2250 or 2280 Credits (15 total Instructor Permissission; may repeat up MATH 3990 Undergraduate Research 1-3 *** credits to 5 cr. -

Supersymmetric Methods in Quantum and Statistical Physics Series: Theoretical and Mathematical Physics
springer.com Georg Junker Supersymmetric Methods in Quantum and Statistical Physics Series: Theoretical and Mathematical Physics The idea of supersymmetry was originally introduced in relativistic quantum field theories as a generalization of Poincare symmetry. In 1976 Nicolai sug• gested an analogous generalization for non-relativistic quantum mechanics. With the one-dimensional model introduced by Witten in 1981, supersym• metry became a major tool in quantum mechanics and mathematical, sta• tistical, and condensed-IIll;l. tter physics. Supersymmetry is also a successful concept in nuclear and atomic physics. An underlying supersymmetry of a given quantum-mechanical system can be utilized to analyze the properties of the system in an elegant and effective way. It is even possible to obtain exact results thanks to supersymmetry. The purpose of this book is to give an introduction to supersymmet• ric quantum mechanics and review some of the Softcover reprint of the original 1st ed. recent developments of vari• ous supersymmetric methods in quantum and statistical physics. 1996, XIII, 172 p. Thereby we will touch upon some topics related to mathematical and condensed-matter physics. A discussion of supersymmetry in atomic and nuclear physics is omit• ted. However, Printed book the reader will find some references in Chap. 9. Similarly, super• symmetric field theories and Softcover supergravity are not considered in this book. In fact, there exist already many excellent 89,99 € | £79.99 | $109.99 textbooks and monographs on these topics. A list may be found in Chap. 9. Yet, it is hoped that [1]96,29 € (D) | 98,99 € (A) | CHF this book may be useful in preparing a footing for a study of supersymmetric theories in 106,50 atomic, nuclear, and particle physics. -
![Arxiv:2012.09211V1 [Math-Ph] 16 Dec 2020](https://docslib.b-cdn.net/cover/3585/arxiv-2012-09211v1-math-ph-16-dec-2020-1053585.webp)
Arxiv:2012.09211V1 [Math-Ph] 16 Dec 2020
Supersymmetry and Representation Theory in Low Dimensions Mathew Calkins1a;b, S. James Gates, Jr.2c;d, and Caroline Klivans3c;e;f aGoogle Search, 111 8th Ave, New York, NY 10011, USA, bCourant Institute of Mathematical Sciences, New York University, 251 Mercer Street, New York, NY 10012, USA cBrown Theoretical Physics Center, Box S, 340 Brook Street, Barus Hall, Providence, RI 02912, USA dDepartment of Physics, Brown University, Box 1843, 182 Hope Street, Barus & Holley, Providence, RI 02912, USA eDivision of Applied Mathematics, Brown University, 182 George Street, Providence, RI 02906, USA and f Institute for Computational & Experimental Research in Mathematics, Brown University, 121 South Main Street Providence, RI 02903, USA ABSTRACT Beginning from a discussion of the known most fundamental dynamical structures of the Standard Model of physics, extended into the realms of math- ematics and theory by the concept of \supersymmetry" or \SUSY," an introduc- tion to efforts to develop a complete representation theory is given. Techniques drawing from graph theory, coding theory, Coxeter Groups, Riemann surfaces, arXiv:2012.09211v1 [math-ph] 16 Dec 2020 and computational approaches to the study of algebraic varieties are briefly highlighted as pathways for future exploration and progress. PACS: 11.30.Pb, 12.60.Jv Keywords: algorithms, off-shell, optimization, supermultiplets, supersymmetry 1 [email protected] 2 sylvester−[email protected] 3 Caroline−[email protected] 1 Supersymmetry and the Standard Model As far as experiments in elementary particle physics reveal, the basic constituents of matter and interactions (i.e. forces excluding gravity) in our universe can be summarized in the list of particles shown in the table indicated in Fig. -

Two Problems in the Theory of Differential Equations
TWO PROBLEMS IN THE THEORY OF DIFFERENTIAL EQUATIONS D. LEITES Abstract. 1) The differential equation considered in terms of exterior differential forms, as E.Cartan´ did, singles out a differential ideal in the supercommutative superalgebra of differential forms, hence an affine supervariety. In view of this observation, it is evident that every differential equation has a supersymmetry (perhaps trivial). Superymmetries of which (systems of) classical differential equations are missed yet? 2) Why criteria of formal integrability of differential equations are never used in practice? To the memory of Ludvig Dmitrievich Faddeev 1. Introduction While the Large Hadron Collider is busy testing (among other things) the existence of supersymmetry in the high energy physics (more correctly, supersymmetry’s applicability to the models), the existence of supersymmetry in the solid body theory (more correctly, its usefulness for describing the models) is proved beyond any doubt, see the excitatory book [Ef], and later works by K. Efetov. Nonholonomic nature of our space-time, suggested in models due to Kaluza–Klein (and seldom remembered Mandel) was usually considered seperately from its super nature. In this note I give examples where the supersymmetry and non-holonomicity manifest themselves in various, sometimes unexpected, instances. In the models of super space-time, and super strings, as well as in the problems spoken about in this note, these notions appear together and interact. L.D. Faddeev would have liked these topics, each of them being related to what used to be of interest to him. Many examples will be only mentioned in passing. 1.1. History: Faddeev–Popov ghosts as analogs of momenta in “odd” mechanics. -

Mathematical Physics – Online Course
Professor: Luis A. Anchordoqui PHY-307 Physics-307: Mathematical Physics – Online course. General Information: This course is classified as "Zero Textbook Cost." The material for the course is available at the course website https://www.lehman.edu/faculty/anchordoqui/307.html I will be posting weekly announcements on blackboard. Each week the same relevant information you would find on the course website will also be posted on blackboard. The course consists of 12 modules. Each module has a synchronous lecture (Thursday from 4:00 to 5:40) and a session of group discussion (Tuesday from 4:00 to 5:40). Asynchronous participation in the discussion board forum is highly recommended. There will be 3 midterm exams (10/01/2020; 11/24/2020; 12/08/2020) and a comprehensive final exam (12/15/2020). At the end of each lecture we will have a quiz related to the material of the previous module. The layout of the document is as follows. We first present the online course development plan. After that we describe the methodology for assessment of student coursework. Finally, we provide some guidelines on how to be successful in the course, and a summary calendar. Contact information: [email protected] Professor: Luis A. Anchordoqui PHY-307 Course Development Plan Module 1 (Online) Date: 08/27/2020 (Lecture) & 09/01/2020 (Group discussion) Topic: Analytic Functions Description: Complex Analysis I: Complex Algebra. Functions of a Complex Variable. Learning Objectives: 1.The educational methodology of this subject proposes to integrate the domain of concepts and knowledge from mathematics into practical application of physics phenomena, and the development of abilities and skills to solve example problems. -

Axiomatic Foundations of Mathematics Ryan Melton Dr
Axiomatic Foundations of Mathematics Ryan Melton Dr. Clint Richardson, Faculty Advisor Stephen F. Austin State University As Bertrand Russell once said, Gödel's Method Pure mathematics is the subject in which we Consider the expression First, Gödel assigned a unique natural number to do not know what we are talking about, or each of the logical symbols and numbers. 2 + 3 = 5 whether what we are saying is true. Russell’s statement begs from us one major This expression is mathematical; it belongs to the field For example: if the symbol '0' corresponds to we call arithmetic and is composed of basic arithmetic question: the natural number 1, '+' to 2, and '=' to 3, then symbols. '0 = 0' '0 + 0 = 0' What is Mathematics founded on? On the other hand, the sentence and '2 + 3 = 5' is an arithmetical formula. 1 3 1 1 2 1 3 1 so each expression corresponds to a sequence. Axioms and Axiom Systems is metamathematical; it is constructed outside of mathematics and labels the expression above as a Then, for this new sequence x1x2x3…xn of formula in arithmetic. An axiom is a belief taken without proof, and positive integers, we associate a Gödel number thus an axiom system is a set of beliefs as follows: x1 x2 x3 xn taken without proof. enc( x1x2x3...xn ) = 2 3 5 ... pn Since Principia Mathematica was such a bold where the encoding is the product of n factors, Consistent? Complete? leap in the right direction--although proving each of which is found by raising the j-th prime nothing about consistency--several attempts at to the xj power.