Geometry and Empirical Science Author(S): C
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Canada Archives Canada Published Heritage Direction Du Branch Patrimoine De I'edition
Rhetoric more geometrico in Proclus' Elements of Theology and Boethius' De Hebdomadibus A Thesis submitted in Candidacy for the Degree of Master of Arts in Philosophy Institute for Christian Studies Toronto, Ontario By Carlos R. Bovell November 2007 Library and Bibliotheque et 1*1 Archives Canada Archives Canada Published Heritage Direction du Branch Patrimoine de I'edition 395 Wellington Street 395, rue Wellington Ottawa ON K1A0N4 Ottawa ON K1A0N4 Canada Canada Your file Votre reference ISBN: 978-0-494-43117-7 Our file Notre reference ISBN: 978-0-494-43117-7 NOTICE: AVIS: The author has granted a non L'auteur a accorde une licence non exclusive exclusive license allowing Library permettant a la Bibliotheque et Archives and Archives Canada to reproduce, Canada de reproduire, publier, archiver, publish, archive, preserve, conserve, sauvegarder, conserver, transmettre au public communicate to the public by par telecommunication ou par Plntemet, prefer, telecommunication or on the Internet, distribuer et vendre des theses partout dans loan, distribute and sell theses le monde, a des fins commerciales ou autres, worldwide, for commercial or non sur support microforme, papier, electronique commercial purposes, in microform, et/ou autres formats. paper, electronic and/or any other formats. The author retains copyright L'auteur conserve la propriete du droit d'auteur ownership and moral rights in et des droits moraux qui protege cette these. this thesis. Neither the thesis Ni la these ni des extraits substantiels de nor substantial extracts from it celle-ci ne doivent etre imprimes ou autrement may be printed or otherwise reproduits sans son autorisation. reproduced without the author's permission. -

Squaring the Circle a Case Study in the History of Mathematics the Problem
Squaring the Circle A Case Study in the History of Mathematics The Problem Using only a compass and straightedge, construct for any given circle, a square with the same area as the circle. The general problem of constructing a square with the same area as a given figure is known as the Quadrature of that figure. So, we seek a quadrature of the circle. The Answer It has been known since 1822 that the quadrature of a circle with straightedge and compass is impossible. Notes: First of all we are not saying that a square of equal area does not exist. If the circle has area A, then a square with side √A clearly has the same area. Secondly, we are not saying that a quadrature of a circle is impossible, since it is possible, but not under the restriction of using only a straightedge and compass. Precursors It has been written, in many places, that the quadrature problem appears in one of the earliest extant mathematical sources, the Rhind Papyrus (~ 1650 B.C.). This is not really an accurate statement. If one means by the “quadrature of the circle” simply a quadrature by any means, then one is just asking for the determination of the area of a circle. This problem does appear in the Rhind Papyrus, but I consider it as just a precursor to the construction problem we are examining. The Rhind Papyrus The papyrus was found in Thebes (Luxor) in the ruins of a small building near the Ramesseum.1 It was purchased in 1858 in Egypt by the Scottish Egyptologist A. -

Pure Mathematics Professors Teaching and Leading Research CO-OP OR REGULAR 28
PURE MATHEMATICS Pure Mathematics professors teaching and leading research CO-OP OR REGULAR 28 Mathematician ranked among top 10 TOP 10 jobs from 2011-2017 – Comcast.com of grads are employed Search for a deeper 96.6% within 2 years understanding of mathematics Pure mathematics is at the foundation of all mathematical reasoning. If first-year calculus ALEX teaches you how to drive the car, Pure Mathematics teaches you how to build one. 3B, PURE MATHEMATICS AND Mathematicians know that there could be no general relativity without differential COMBINATORICS AND geometry, and no computer security without advanced number theory. OPTIMIZATION Pure Mathematics at Waterloo is a small, cohesive, and challenging program that will open countless doors for you. Our graduates have used the program as a springboard into careers WHAT DO YOU LOVE ABOUT in information technology, finance, business, science, education, and insurance, often by way PURE MATHEMATICS? The satisfaction from understanding of some of the most prestigious graduate programs in the world. an idea at a deeper level and tying together unrelated branches of ALEX’S FAVOURITE COURSES mathematics or physics for the › PMATH 320 Euclidean Geometry: This course is everything you love about Geometry: first time is the most rewarding Euclid’s axioms, isometries of the Euclidean plane and of Euclidean space, polygons, part of learning and understanding polyhedral, polytopes, and the kissing problem. mathematics. What I really enjoy is › PMATH 351 Real Analysis: It’s a very intuitive and natural approach to real analysis, and the developing a deep understanding of complexity of the course builds very naturally to the end of the semester. -

Can One Design a Geometry Engine? on the (Un) Decidability of Affine
Noname manuscript No. (will be inserted by the editor) Can one design a geometry engine? On the (un)decidability of certain affine Euclidean geometries Johann A. Makowsky Received: June 4, 2018/ Accepted: date Abstract We survey the status of decidabilty of the consequence relation in various ax- iomatizations of Euclidean geometry. We draw attention to a widely overlooked result by Martin Ziegler from 1980, which proves Tarski’s conjecture on the undecidability of finitely axiomatizable theories of fields. We elaborate on how to use Ziegler’s theorem to show that the consequence relations for the first order theory of the Hilbert plane and the Euclidean plane are undecidable. As new results we add: (A) The first order consequence relations for Wu’s orthogonal and metric geometries (Wen- Ts¨un Wu, 1984), and for the axiomatization of Origami geometry (J. Justin 1986, H. Huzita 1991) are undecidable. It was already known that the universal theory of Hilbert planes and Wu’s orthogonal geom- etry is decidable. We show here using elementary model theoretic tools that (B) the universal first order consequences of any geometric theory T of Pappian planes which is consistent with the analytic geometry of the reals is decidable. The techniques used were all known to experts in mathematical logic and geometry in the past but no detailed proofs are easily accessible for practitioners of symbolic computation or automated theorem proving. Keywords Euclidean Geometry · Automated Theorem Proving · Undecidability arXiv:1712.07474v3 [cs.SC] 1 Jun 2018 J.A. Makowsky Faculty of Computer Science, Technion–Israel Institute of Technology, Haifa, Israel E-mail: [email protected] 2 J.A. -

Pure Mathematics
Why Study Mathematics? Mathematics reveals hidden patterns that help us understand the world around us. Now much more than arithmetic and geometry, mathematics today is a diverse discipline that deals with data, measurements, and observations from science; with inference, deduction, and proof; and with mathematical models of natural phenomena, of human behavior, and social systems. The process of "doing" mathematics is far more than just calculation or deduction; it involves observation of patterns, testing of conjectures, and estimation of results. As a practical matter, mathematics is a science of pattern and order. Its domain is not molecules or cells, but numbers, chance, form, algorithms, and change. As a science of abstract objects, mathematics relies on logic rather than on observation as its standard of truth, yet employs observation, simulation, and even experimentation as means of discovering truth. The special role of mathematics in education is a consequence of its universal applicability. The results of mathematics--theorems and theories--are both significant and useful; the best results are also elegant and deep. Through its theorems, mathematics offers science both a foundation of truth and a standard of certainty. In addition to theorems and theories, mathematics offers distinctive modes of thought which are both versatile and powerful, including modeling, abstraction, optimization, logical analysis, inference from data, and use of symbols. Mathematics, as a major intellectual tradition, is a subject appreciated as much for its beauty as for its power. The enduring qualities of such abstract concepts as symmetry, proof, and change have been developed through 3,000 years of intellectual effort. Like language, religion, and music, mathematics is a universal part of human culture. -
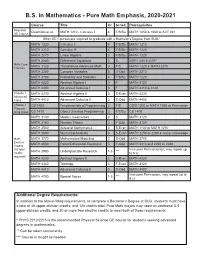
B.S. in Mathematics - Pure Math Emphasis, 2020-2021
B.S. in Mathematics - Pure Math Emphasis, 2020-2021 Course Title Cr. Sched. Prerequisites Required Quantitative Lit. MATH 1210 - Calculus I 4 F/S/Su MATH 1050 & 1060 or ACT 26+ GE Course Other GE Courses are required to graduate with a Bachelor’s Degree from SUU.* MATH 1220 Calculus II 4 F/S/Su MATH 1210 MATH 2210 Calculus III 4 F/S/Su MATH 1220 MATH 2270 Linear Algebra 3 F/S/Su MATH 1220 MATH 2280 Differential Equations 3 S MATH 1220 & 2270** Math Core MATH 3120 Transition to Advanced Math 3 F/S MATH 1220 & MATH 2270 Courses MATH 3250 Complex Variables 3 S-Odd MATH 2210 MATH 3700 Probability and Statistics 4 F/S/Su MATH 1220 MATH 4220 Abstract Algebra I 3 F MATH 3120 MATH 4400 Advanced Calculus I 3 F MATH 2210 & 3120 Choose 1 MATH 4230 Abstract Algebra II 3 S-Even MATH 4220 Advanced Class MATH 4410 Advanced Calculus II 3 S-Odd MATH 4400 Choose 1 CS 1400 Fundamentals of Programming 3 F/S CSIS 1030 or MATH 1050 or Permission Program- ming Class CS 1410 Object Oriented Programming 3 F/S/Su CS 1400 MATH 3130 Modern Geometries 3 S MATH 3120 MATH 3160 Number Theory 3 F-Odd MATH 3120 MATH 3500 Actuarial Mathematics 3 S-Even MATH 1100 or MATH 1210 MATH 3600 Numerical Analysis 3 S-Even MATH 2250 or 2280 & comp. knowledge Math MATH 3770 Mathematical Modeling 3 S-Odd MATH 3700 Elective MATH 3800 Partial Differential Equations 3 F-Odd MATH 2210 and 2250 or 2280 Credits (15 total Instructor Permissission; may repeat up MATH 3990 Undergraduate Research 1-3 *** credits to 5 cr. -

A CONCISE MINI HISTORY of GEOMETRY 1. Origin And
Kragujevac Journal of Mathematics Volume 38(1) (2014), Pages 5{21. A CONCISE MINI HISTORY OF GEOMETRY LEOPOLD VERSTRAELEN 1. Origin and development in Old Greece Mathematics was the crowning and lasting achievement of the ancient Greek cul- ture. To more or less extent, arithmetical and geometrical problems had been ex- plored already before, in several previous civilisations at various parts of the world, within a kind of practical mathematical scientific context. The knowledge which in particular as such first had been acquired in Mesopotamia and later on in Egypt, and the philosophical reflections on its meaning and its nature by \the Old Greeks", resulted in the sublime creation of mathematics as a characteristically abstract and deductive science. The name for this science, \mathematics", stems from the Greek language, and basically means \knowledge and understanding", and became of use in most other languages as well; realising however that, as a matter of fact, it is really an art to reach new knowledge and better understanding, the Dutch term for mathematics, \wiskunde", in translation: \the art to achieve wisdom", might be even more appropriate. For specimens of the human kind, \nature" essentially stands for their organised thoughts about sensations and perceptions of \their worlds outside and inside" and \doing mathematics" basically stands for their thoughtful living in \the universe" of their idealisations and abstractions of these sensations and perceptions. Or, as Stewart stated in the revised book \What is Mathematics?" of Courant and Robbins: \Mathematics links the abstract world of mental concepts to the real world of physical things without being located completely in either". -
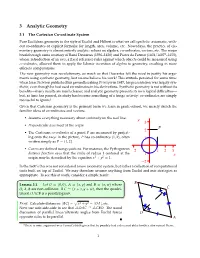
3 Analytic Geometry
3 Analytic Geometry 3.1 The Cartesian Co-ordinate System Pure Euclidean geometry in the style of Euclid and Hilbert is what we call synthetic: axiomatic, with- out co-ordinates or explicit formulæ for length, area, volume, etc. Nowadays, the practice of ele- mentary geometry is almost entirely analytic: reliant on algebra, co-ordinates, vectors, etc. The major breakthrough came courtesy of Rene´ Descartes (1596–1650) and Pierre de Fermat (1601/16071–1655), whose introduction of an axis, a fixed reference ruler against which objects could be measured using co-ordinates, allowed them to apply the Islamic invention of algebra to geometry, resulting in more efficient computations. The new geometry was revolutionary, so much so that Descartes felt the need to justify his argu- ments using synthetic geometry, lest no-one believe his work! This attitude persisted for some time: when Issac Newton published his groundbreaking Principia in 1687, his presentation was largely syn- thetic, even though he had used co-ordinates in his derivations. Synthetic geometry is not without its benefits—many results are much cleaner, and analytic geometry presents its own logical difficulties— but, as time has passed, its study has become something of a fringe activity: co-ordinates are simply too useful to ignore! Given that Cartesian geometry is the primary form we learn in grade-school, we merely sketch the familiar ideas of co-ordinates and vectors. • Assume everything necessary about on the real line. continuity y 3 • Perpendicular axes meet at the origin. P 2 • The Cartesian co-ordinates of a point P are measured by project- ing onto the axes: in the picture, P has co-ordinates (1, 2), often 1 written simply as P = (1, 2). -

Synthetic and Analytic Geometry
CHAPTER I SYNTHETIC AND ANALYTIC GEOMETRY The purpose of this chapter is to review some basic facts from classical deductive geometry and coordinate geometry from slightly more advanced viewpoints. The latter reflect the approaches taken in subsequent chapters of these notes. 1. Axioms for Euclidean geometry During the 19th century, mathematicians recognized that the logical foundations of their subject had to be re-examined and strengthened. In particular, it was very apparent that the axiomatic setting for geometry in Euclid's Elements requires nontrivial modifications. Several ways of doing this were worked out by the end of the century, and in 1900 D. Hilbert1 (1862{1943) gave a definitive account of the modern foundations in his highly influential book, Foundations of Geometry. Mathematical theories begin with primitive concepts, which are not formally defined, and as- sumptions or axioms which describe the basic relations among the concepts. In Hilbert's setting there are six primitive concepts: Points, lines, the notion of one point lying between two others (betweenness), congruence of segments (same distances between the endpoints) and congruence of angles (same angular measurement in degrees or radians). The axioms on these undefined concepts are divided into five classes: Incidence, order, congruence, parallelism and continuity. One notable feature of this classification is that only one class (congruence) requires the use of all six primitive concepts. More precisely, the concepts needed for the axiom classes are given as follows: Axiom class Concepts required Incidence Point, line, plane Order Point, line, plane, betweenness Congruence All six Parallelism Point, line, plane Continuity Point, line, plane, betweenness Strictly speaking, Hilbert's treatment of continuity involves congruence of segments, but the continuity axiom may be formulated without this concept (see Forder, Foundations of Euclidean Geometry, p. -

Axiomatic Foundations of Mathematics Ryan Melton Dr
Axiomatic Foundations of Mathematics Ryan Melton Dr. Clint Richardson, Faculty Advisor Stephen F. Austin State University As Bertrand Russell once said, Gödel's Method Pure mathematics is the subject in which we Consider the expression First, Gödel assigned a unique natural number to do not know what we are talking about, or each of the logical symbols and numbers. 2 + 3 = 5 whether what we are saying is true. Russell’s statement begs from us one major This expression is mathematical; it belongs to the field For example: if the symbol '0' corresponds to we call arithmetic and is composed of basic arithmetic question: the natural number 1, '+' to 2, and '=' to 3, then symbols. '0 = 0' '0 + 0 = 0' What is Mathematics founded on? On the other hand, the sentence and '2 + 3 = 5' is an arithmetical formula. 1 3 1 1 2 1 3 1 so each expression corresponds to a sequence. Axioms and Axiom Systems is metamathematical; it is constructed outside of mathematics and labels the expression above as a Then, for this new sequence x1x2x3…xn of formula in arithmetic. An axiom is a belief taken without proof, and positive integers, we associate a Gödel number thus an axiom system is a set of beliefs as follows: x1 x2 x3 xn taken without proof. enc( x1x2x3...xn ) = 2 3 5 ... pn Since Principia Mathematica was such a bold where the encoding is the product of n factors, Consistent? Complete? leap in the right direction--although proving each of which is found by raising the j-th prime nothing about consistency--several attempts at to the xj power. -

A Survey of the Development of Geometry up to 1870
A Survey of the Development of Geometry up to 1870∗ Eldar Straume Department of mathematical sciences Norwegian University of Science and Technology (NTNU) N-9471 Trondheim, Norway September 4, 2014 Abstract This is an expository treatise on the development of the classical ge- ometries, starting from the origins of Euclidean geometry a few centuries BC up to around 1870. At this time classical differential geometry came to an end, and the Riemannian geometric approach started to be developed. Moreover, the discovery of non-Euclidean geometry, about 40 years earlier, had just been demonstrated to be a ”true” geometry on the same footing as Euclidean geometry. These were radically new ideas, but henceforth the importance of the topic became gradually realized. As a consequence, the conventional attitude to the basic geometric questions, including the possible geometric structure of the physical space, was challenged, and foundational problems became an important issue during the following decades. Such a basic understanding of the status of geometry around 1870 enables one to study the geometric works of Sophus Lie and Felix Klein at the beginning of their career in the appropriate historical perspective. arXiv:1409.1140v1 [math.HO] 3 Sep 2014 Contents 1 Euclideangeometry,thesourceofallgeometries 3 1.1 Earlygeometryandtheroleoftherealnumbers . 4 1.1.1 Geometric algebra, constructivism, and the real numbers 7 1.1.2 Thedownfalloftheancientgeometry . 8 ∗This monograph was written up in 2008-2009, as a preparation to the further study of the early geometrical works of Sophus Lie and Felix Klein at the beginning of their career around 1870. The author apologizes for possible historiographic shortcomings, errors, and perhaps lack of updated information on certain topics from the history of mathematics. -

Is Geometry Analytic? Mghanga David Mwakima
IS GEOMETRY ANALYTIC? MGHANGA DAVID MWAKIMA 1. INTRODUCTION In the fourth chapter of Language, Truth and Logic, Ayer undertakes the task of showing how a priori knowledge of mathematics and logic is possible. In doing so, he argues that only if we understand mathematics and logic as analytic,1 by which he memorably meant “devoid of factual content”2, do we have a justified account of 3 a priori knowledgeδιανοια of these disciplines. In this chapter, it is not clear whether Ayer gives an argument per se for the analyticity of mathematics and logic. For when one reads that chapter, one sees that Ayer is mainly criticizing the views held by Kant and Mill with respect to arithmetic.4 Nevertheless, I believe that the positive argument is present. Ayer’s discussion of geometry5 in this chapter shows that it is this discussion which constitutes his positive argument for the thesis that analytic sentences are true 1 Now, I am aware that ‘analytic’ was understood differently by Kant, Carnap, Ayer, Quine, and Putnam. It is not even clear whether there is even an agreed definition of ‘analytic’ today. For the purposes of my paper, the meaning of ‘analytic’ is Carnap’s sense as described in: Michael, Friedman, Reconsidering Logical Positivism (New York: Cambridge University Press, 1999), in terms of the relativized a priori. 2 Alfred Jules, Ayer, Language, Truth and Logic (New York: Dover Publications, 1952), p. 79, 87. In these sections of the book, I think the reason Ayer chose to characterize analytic statements as “devoid of factual” content is in order to give an account of why analytic statements could not be shown to be false on the basis of observation.