DOCSLIB.ORG

Primary Cervical Spine Ligaments

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Primary Cervical Spine Ligaments Strain Rate Dependent Properties of Younger Human Cervical Spine Ligaments by Stephen Mattucci A thesis presented to the University of Waterloo in fulfillment of the thesis requirement for the degree of Master of Applied Science in Mechanical Engineering Waterloo, Ontario, Canada, 2011 ©Stephen Mattucci 2011 AUTHOR'S DECLARATION I hereby declare that I am the sole author of this thesis. This is a true copy of the thesis, including any required final revisions, as accepted by my examiners. I understand that my thesis may be made electronically available to the public. Stephen Frank Ernesto Mattucci ii Abstract The cervical spine ligaments play an essential role in limiting the physiological ranges of motion in the neck; however, traumatic loading such as that experienced in automotive crash scenarios can lead to ligament damage and result in neck injury. The development of detailed finite element models for injury simulation requires accurate ligament mechanical properties at relevant loading rates. The objective of this research was to provide detailed mechanical properties for the cervical spine ligaments, by performing tensile tests at elongation rates relevant to automobile crash scenarios, using younger specimens (less than 50 years old), and to provide a comprehensive investigation of spinal level and gender effects. The five primary ligaments (present between C2-T1) investigated were: the anterior longitudinal ligament, posterior longitudinal ligament, capsular ligament, ligamentum flavum, and interspinous ligament. The craniovertebral ligaments (Skull/C0-C2) investigated were the tectorial membrane/vertical cruciate/apical/alar ligament complex, transverse ligament, anterior atlanto- occipital membrane, posterior atlanto-occipital membrane, anterior atlanto-axial membrane, and posterior atlanto-axial membrane. Tests were performed within an environmental chamber designed to mimic in vivo temperature and humidity conditions, and specimens were preconditioned for 20 cycles at 10% strain prior to testing to failure. Ligaments were tested at quasi-static (0.5s-1), medium (20s-1) and high (150-250s-1). These strain rates were predicted by an existing cervical spine finite element model under typical crash scenarios. Two hundred sixty-one total primary ligament tests were performed, with approximately even distribution within elongation rate, spinal level, and gender. Another forty-four craniovertebral ligaments were tested. Results were plotted as force-displacement curves and the response characteristics determined from the curves were: failure force, failure elongation, stiffness of the linear region, toe region elongation, failure stress, failure strain, modulus and toe region strain. The measured force-displacement data followed expected trends when compared with previous studies. The younger ligaments had less scatter, and were both stiffer and stronger than the older specimens that were reported in previous studies at both quasi-static and comparable higher elongation rates. iii Statistical analysis was performed on the results to establish significant effects. Strain rate effects were most significant whereas spinal level effects were not found. In general, gender effects were not found to be significantly different, but consistent trends were identified with male ligaments having a higher stiffness and failure force than female ligaments. The post-ultimate load region of the curves was reported to offer insight into the ligament failure mechanism. The characteristic values obtained were used to develop average curves for each ligament, with the intention to eventually be directly integrated into finite element models to better represent the ligament structures. Curves were developed to incorporate the strain rate, spinal level and gender effects for each ligament based on the statistical analyses. Post-failure response was incorporated into these curves because this region has been shown to have an effect on neck behaviour in mathematical models. Recommendations for future studies include measuring accurate cross sectional areas of ligaments during tensile testing to obtain true stress and true strain measurements to better understand if differences in mechanical properties are structural or material. Other possible improvements would be further testing of young cervical spine ligaments with larger sample sizes to further explore spinal level and gender effects. Additional testing performed under identical testing conditions as the current study would allow for pooling of the results effectively increasing the sample size. iv Acknowledgements There are several people I would like to thank who played a role in my life during my time at the University of Waterloo working on my masters, both at school and in my life outside of school (however non-existent it seemed at times). I would like to thank my supervisors; Dr. Duane Cronin and Dr. Naveen Chandrashekar for their knowledge and guidance. They have introduced me to academic research and the entire process from identifying the problem to interpreting results, and shown me what it takes to produce valuable work. I am happy to thank the Global Human Body Model Consortium (GHBMC) for providing the motivation and funding behind this project. This research would not have been possible without their support. Specifically I would like to thank Dr. Yibing Shi and Dr. Zine Ben Aoun for providing a valuable external opinion and helping to bridge the gap between industry and academia. I would also like to thank my family; my parents, Kathy and Domenic, and sister Aly. Your unwavering support and unconditional love has always provided me with the extra push in times of need. My grandparents; Frank Ridler, and Theresa and Ernesto Mattucci. Your accomplishments in life have provided me with the opportunities I have had, and for that I am truly grateful. v Dedication I would like to dedicate this work to my sister Aly Mattucci. The challenges you overcome on a daily basis make me believe that anything is possible. You provide me with more inspiration and motivation than you could ever know. vi Table of Contents AUTHOR'S DECLARATION ............................................................................................................ ii Abstract ................................................................................................................................................ iii Acknowledgements ............................................................................................................................... v Dedication............................................................................................................................................. vi Table of Contents ................................................................................................................................ vii List of Figures ..................................................................................................................................... xii List of Tables ....................................................................................................................................... xv Chapter 1 Introduction ........................................................................................................................ 1 1.1 Motivation for Research ............................................................................................................... 1 1.2 Research Objectives and Approach .............................................................................................. 3 1.3 Thesis Outline ............................................................................................................................... 4 Chapter 2 Anatomy and Physiology ................................................................................................... 6 2.1 Anatomical Terminology.............................................................................................................. 6 2.1.1 Anatomical Directions ........................................................................................................... 6 2.1.2 Anatomical Sections and Planes ............................................................................................ 8 2.2 Vertebrae ...................................................................................................................................... 9 2.2.1 Cervical Vertebrae ............................................................................................................... 11 vii 2.2.2 C1 Vertebra (Atlas) ............................................................................................................. 15 2.2.3 C2 Vertebra (Axis) .............................................................................................................. 16 2.3 Facet Joints ................................................................................................................................. 19 2.4 Intervertebral Disc ...................................................................................................................... 20 2.5 Cervical Spine Ligaments........................................................................................................... 24 2.5.1 Primary Cervical Spine Ligaments ...................................................................................... 25 2.5.2 Craniovertebral Ligaments .................................................................................................
Load more

Recommended publications
  • Synovial Joints Permit Movements of the Skeleton
    8 Joints Lecture Presentation by Lori Garrett © 2018 Pearson Education, Inc. Section 1: Joint Structure and Movement Learning Outcomes 8.1 Contrast the major categories of joints, and explain the relationship between structure and function for each category. 8.2 Describe the basic structure of a synovial joint, and describe common accessory structures and their functions. 8.3 Describe how the anatomical and functional properties of synovial joints permit movements of the skeleton. © 2018 Pearson Education, Inc. Section 1: Joint Structure and Movement Learning Outcomes (continued) 8.4 Describe flexion/extension, abduction/ adduction, and circumduction movements of the skeleton. 8.5 Describe rotational and special movements of the skeleton. © 2018 Pearson Education, Inc. Module 8.1: Joints are classified according to structure and movement Joints, or articulations . Locations where two or more bones meet . Only points at which movements of bones can occur • Joints allow mobility while preserving bone strength • Amount of movement allowed is determined by anatomical structure . Categorized • Functionally by amount of motion allowed, or range of motion (ROM) • Structurally by anatomical organization © 2018 Pearson Education, Inc. Module 8.1: Joint classification Functional classification of joints . Synarthrosis (syn-, together + arthrosis, joint) • No movement allowed • Extremely strong . Amphiarthrosis (amphi-, on both sides) • Little movement allowed (more than synarthrosis) • Much stronger than diarthrosis • Articulating bones connected by collagen fibers or cartilage . Diarthrosis (dia-, through) • Freely movable © 2018 Pearson Education, Inc. Module 8.1: Joint classification Structural classification of joints . Fibrous • Suture (sutura, a sewing together) – Synarthrotic joint connected by dense fibrous connective tissue – Located between bones of the skull • Gomphosis (gomphos, bolt) – Synarthrotic joint binding teeth to bony sockets in maxillae and mandible © 2018 Pearson Education, Inc.
    [Show full text]
  • Diagnosis of Atlantoaxial Instability Requires Clinical Suspicion To
    al of S rn pi ou n Henderson Sr and Henderson Jr, J Spine 2017, 6:2 J e Journal of Spine DOI: 10.4172/2165-7939.1000364 ISSN: 2165-7939 Mini Review OMICS International Diagnosis of Atlantoaxial Instability Requires Clinical Suspicion to Drive the Radiological Investigation Fraser C Henderson Sr.1,2* and Fraser C Henderson Jr.3 1Doctors Community Hospital, Lanham, MD, USA 2The Metropolitan Neurosurgery Group, LLC, Chevy Chase, MD, USA 3Medical University of South Carolina, Charleston, SC, USA Introduction bending to the contralateral side, are often injured in motor vehicle collisions, and could be implicated in whiplash-associated disorders Atlantoaxial instability (AAI) occurs as a result of trauma, [15]. Failure of the alar ligament allows a 30% increased rotation to congenital conditions such as os odontoideum, neoplasm, infection the opposite side [16]. The atlantoaxial joint is ill-equipped to handle and degenerative connective tissue disorders such as rheumatoid the required multi-axial movements in the presence of ligamentous arthritis, genetic conditions such as HOX-D3 and Down syndrome, laxity or disruption [17]. Weakness of the muscles and ligaments, and heritable connective tissue disorders, emblematic of which are hormonal changes, infection, immunological problems, and congenital the Ehlers Danlos syndromes (EDS). Prototypical of disorders in dysmorphism may contribute to the overall mechanical dysfunction at which AAI is diagnosed, is rheumatoid arthritis (RA). Prior to the the C1-C2 motion segment. development of effective disease-modifying pharmacotherapies, 88% of RA patients exhibited radiographic evidence of C1-C2 involvement, Hypermobility of the AAJ is common in children, and up to 45° of in whom 49% were symptomatic and 20% myelopathic; ultimately, rotation may be observed in each direction.
    [Show full text]
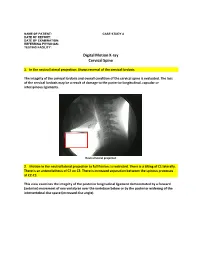
  • Digital Motion X-Ray Cervical Spine
    NAME OF PATIENT: CASE STUDY 4 DATE OF REPORT: DATE OF EXAMINATION: REFERRING PHYSICIAN: TESTING FACILITY: Digital Motion X-ray Cervical Spine 1. In the neutral lateral projection: Shows reversal of the cervical lordosis. The integrity of the cervical lordosis and overall condition of the cervical spine is evaluated. The loss of the cervical lordosis may be a result of damage to the posterior longitudinal, capsular or interspinous ligaments. Neutral lateral projection 2. Motion in the neutral lateral projection to full flexion: Is restricted. There is a tilting of C1 laterally. There is an anterolisthesis of C2 on C3. There is increased separation between the spinous processes at C2-C3. This view examines the integrity of the posterior longitudinal ligament demonstrated by a forward (anterior) movement of one vertebrae over the vertebrae below or by the posterior widening of the intervertebral disc space (increased disc angle). Widening of posterior disc space Anterolisthesis The integrity of the interspinous ligament is evaluated in the lateral flexion view. Damage to this ligament results in increased separation of the spinous processes in flexion. Damaged Interspinous Ligament Full flexion projection 3. Motion in the neutral lateral projection to full extension: Is restricted. There is a retrolisthesis of C4 on C5. This view examines the integrity of the anterior longitudinal ligament demonstrated by a backward (posterior) movement of one vertebrae over the vertebrae below or by the anterior widening of the intervertebral disc space (increased disc angle). Retrolisthesis Widening of the anterior disc Full Extension 4. Motion in the oblique flexion projection: Is restricted. There is gapping of the facet joints at C6-C7 bilaterally and C7-T1 bilaterally.
    [Show full text]
  • Epithelia Joitns
    NAME LOCATION STRUCTURE FUNCTION MOVEMENT Temporomandibular joint Condylar head of ramus of Synovial Diarthrosis Modified hinge joint mandible and glenoid fossa of Rotation and gliding temporal bone Biaxial Zygapophyseal joint Between articular processes of Synovial Diarthrosis Gliding 2 adjacent vertebrae Non axial Atlanto-Occipital joints Atlas and occipital condyle of Synovial Diarthrosis Ellipsoid occipital bone Biaxial Atlantoaxial joints Atlas and axis Synovial Diarthrosis Pivot Uniaxial Joints of vertebral arches Ligaments Fibrous Amphiarthrosis Syndesmoses Intervertebral symphyseal Intervertebral disk between 2 Cartilaginous Amphiarthrosis joints vertebrae Symphysis Costovertebral Head of ribs and body of Synovial Diarthrosis Gliding thoracic vertebra Non axial Costotrasnverse joints Tubercle of rib and transverse Synovial Diarthrosis Gliding process of thoracic vertebra Non axial Lumbosacral Joint Left and right zygopophyseal Laterally Synovial joint Intervertebral symphyseal joint Symphysis SternoclavicularJoint Clavicular notch articulates Synovial Diarthrosis Gliding with medial ends of clavicle Non Axial Manubriosternal Joint Hyaline cartilage junction Cartilaginous Synarthrosis Sternal Angle between manubrium and body Symphysis Xiphisternal Joint Cartilage between xiphoid Synchondrosis Synarthrosis process and body Synostoses Sternocostal Joint (1st) Costocartilage 1 with sternum Cartilaginous Synchondrosis Synarthrosis NAME Location Section Anterior longitudinal runs down anterior surface of vertebral body Vertebral column ligament Posterior longitudinal in canal, runs down posterior surface of vertebral body ligament Interspinous ligament Connects spinous processes Ligamentum flavum Connects laminae ! Intra-articular Disc Between articulating surface of sternum and clavicle Sternoclavicular Joint Costoclavicular ligament 1st rib to clavicle !.
    [Show full text]
  • Duplication of the Alar Ligaments: a Case Report
    Open Access Case Report DOI: 10.7759/cureus.2893 Duplication of the Alar Ligaments: A Case Report Asad Rizvi 1 , Joe Iwanaga 2 , Rod J. Oskouian 3 , Marios Loukas 4 , R. Shane Tubbs 5 1. St. Georges University School of Medicine, St. Georges, GRD 2. Seattle Science Foundation, Seattle, USA 3. Neurosurgery, Swedish Neuroscience Institute, Seattle, USA 4. Anatomical Sciences, St. George's University, St. George's, GRD 5. Neurosurgery, Seattle Science Foundation, Seattle, USA Corresponding author: Joe Iwanaga, [email protected] Abstract The alar ligament is one of the two strongest ligaments stabilizing the craniocervical junction. The literature describes many variations of the attachment, insertion, shape, and orientation of the alar ligament and an understanding of these variations is vital as they can lead to altered biomechanics or misinterpretation on imaging. Herein, we report, to our knowledge, the first case of duplication of the alar ligaments and discuss the anatomical variations present in the literature. Categories: Neurology, Pathology Keywords: alar ligament, duplication, craniocervical junction, variant, transverse occipital ligament, anatomy Introduction The craniocervical junction is composed of the atlantooccipital and the atlantoaxial joints. Several ligaments stabilize these joints, namely the transverse, alar, transverse occipital, accessory, lateral atlantooccipital, and apical ligaments [1]. The transverse and alar ligaments are the two strongest ligaments stabilizing the craniocervical junction with approximately 400 N and 200 N necessary until failure, respectively [1-2]. The alar ligaments are fibrous cords that attach to the dens bilaterally and insert on the base of the skull. They function to limit axial rotation and lateral bending on the contralateral side, and flexion secondarily [1- 2].
    [Show full text]
  • Posterior Longitudinal Ligament Status in Cervical Spine Bilateral Facet Dislocations
    Thomas Jefferson University Jefferson Digital Commons Department of Orthopaedic Surgery Faculty Papers Department of Orthopaedic Surgery November 2005 Posterior longitudinal ligament status in cervical spine bilateral facet dislocations John A. Carrino Harvard Medical School & Brigham and Women's Hospital Geoffrey L. Manton Thomas Jefferson University Hospital William B. Morrison Thomas Jefferson University Hospital Alex R. Vaccaro Thomas Jefferson University Hospital and The Rothman Institute Mark E. Schweitzer New York University & Hospital for Joint Diseases Follow this and additional works at: https://jdc.jefferson.edu/orthofp Part of the Orthopedics Commons LetSee next us page know for additional how authors access to this document benefits ouy Recommended Citation Carrino, John A.; Manton, Geoffrey L.; Morrison, William B.; Vaccaro, Alex R.; Schweitzer, Mark E.; and Flanders, Adam E., "Posterior longitudinal ligament status in cervical spine bilateral facet dislocations" (2005). Department of Orthopaedic Surgery Faculty Papers. Paper 3. https://jdc.jefferson.edu/orthofp/3 This Article is brought to you for free and open access by the Jefferson Digital Commons. The Jefferson Digital Commons is a service of Thomas Jefferson University's Center for Teaching and Learning (CTL). The Commons is a showcase for Jefferson books and journals, peer-reviewed scholarly publications, unique historical collections from the University archives, and teaching tools. The Jefferson Digital Commons allows researchers and interested readers anywhere in the world to learn about and keep up to date with Jefferson scholarship. This article has been accepted for inclusion in Department of Orthopaedic Surgery Faculty Papers by an authorized administrator of the Jefferson Digital Commons. For more information, please contact: [email protected].
    [Show full text]
  • Variability of Morphology and Signal Intensity of Alar Ligaments in Healthy Volunteers Using MR ORIGINAL RESEARCH Imaging
    Variability of Morphology and Signal Intensity of Alar Ligaments in Healthy Volunteers Using MR ORIGINAL RESEARCH Imaging N. Lummel BACKGROUND AND PURPOSE: Evaluation of alar traumatic injuries by using MR imaging is frequently C. Zeif performed. This study investigates the variability of morphology and signal intensity of alar ligaments in healthy volunteers so that pathology can be more accurately defined. A. Kloetzer J. Linn MATERIALS AND METHODS: Fifty healthy volunteers were examined on a 1.5T MR imaging scanner Ϫ H. Bru¨ ckmann with 2-mm PD weighted sequences in 3 planes. Delineation of the alar ligaments in 3 planes and signal-intensity characteristics on sagittal planes were analyzed by using a 4-point grading scale. H. Bitterling Variability of courses and morphologic characteristics were described. RESULTS: Delineation of alar ligaments was best viewed in the coronal plane, followed by the sagittal and axial planes. In the sagittal view, 6.5% of alar ligaments appeared homogeneously dark. Hyper- intense signal intensity in up to one-third of the cross-sectional area was present in 33% of cases; in up to two-thirds of the cross-sectional area, in 45% of cases; and in more than two-thirds of the cross-sectional area, in 15% of cases. Of alar ligaments, 58.5% ascended laterally, 40.5% ran horizontally, and 1% descended laterally. The cross-sectional area was round in 41.5%, oval in 51.5%, and winglike in 6.5%. CONCLUSIONS: On 1.5T MR imaging, the alar ligaments can be delineated best in the coronal and sagittal planes. Our data indicate a remarkable variability of morphology and course as well as signal intensity.
    [Show full text]
  • Diagnostic Utility of Increased STIR Signal in the Posterior Atlanto-Occipital and Atlantoaxial Membrane Complex on MRI in Acute C1–C2 Fracture
    Published July 6, 2017 as 10.3174/ajnr.A5284 ORIGINAL RESEARCH SPINE Diagnostic Utility of Increased STIR Signal in the Posterior Atlanto-Occipital and Atlantoaxial Membrane Complex on MRI in Acute C1–C2 Fracture X Y.-M. Chang, X G. Kim, X N. Peri, X E. Papavassiliou, X R. Rojas, and X R.A. Bhadelia ABSTRACT BACKGROUND AND PURPOSE: Acute C1–C2 fractures are difficult to detect on MR imaging due to a paucity of associated bone marrow edema. The purpose of this study was to determine the diagnostic utility of increased STIR signal in the posterior atlanto-occipital and atlantoaxial membrane complex (PAOAAM) in the detection of acute C1–C2 fractures on MR imaging. MATERIALS AND METHODS: Eighty-seven patients with C1–C2 fractures, 87 with no fractures, and 87 with other cervical fractures with acute injury who had both CT and MR imaging within 24 hours were included. All MR images were reviewed by 2 neuroradiologists for the presence of increased STIR signal in the PAOAAM and interspinous ligaments at other cervical levels. Sensitivity and specificity of increased signal within the PAOAAM for the presence of a C1–C2 fracture were assessed. RESULTS: Increased PAOAAM STIR signal was seen in 81/87 patients with C1–C2 fractures, 6/87 patients with no fractures, and 51/87 patients with other cervical fractures with 93.1% sensitivity versus those with no fractures, other cervical fractures, and all controls. Specificity was 93.1% versus those with no fractures, 41.4% versus those with other cervical fractures, and 67.2% versus all controls for the detection of acute C1–C2 fractures.
    [Show full text]
  • Biomechanics of the Cervical Spine. I
    Clinical Biomechanics 15 (2000) 633±648 www.elsevier.com/locate/clinbiomech Review paper Biomechanics of the cervical spine. I: Normal kinematics Nikolai Bogduk a,*, Susan Mercer b a Newcastle Bone and Joint Institute, University of Newcastle, Royal Newcastle Hospital, Level 4, David Maddison Building, Newcastle, NSW 2300, Australia b Department of Anatomy, University of Otago, Dunedin, New Zealand Abstract This review constitutes the ®rst of four reviews that systematically address contemporary knowledge about the mechanical behavior of the cervical vertebrae and the soft-tissues of the cervical spine, under normal conditions and under conditions that result in minor or major injuries. This ®rst review considers the normal kinematics of the cervical spine, which predicates the appreciation of the biomechanics of cervical spine injury. It summarizes the cardinal anatomical features of the cervical spine that determine how the cervical vertebrae and their joints behave. The results are collated of multiple studies that have measured the range of motion of individual joints of the cervical spine. However, modern studies are highlighted that reveal that, even under normal conditions, range of motion is not consistent either in time or according to the direction of motion. As well, detailed studies are summarized that reveal the order of movement of individual vertebrae as the cervical spine ¯exes or extends. The review concludes with an account of the location of instantaneous centres of rotation and their biological basis. Relevance The facts and precepts covered in this review underlie many observations that are critical to comprehending how the cervical spine behaves under adverse conditions, and how it might be injured.
    [Show full text]
  • Supraspinous Ligament Sprains
    Unraveling the Mystery of Low Back Pain #5: Supraspinous Ligament Sprains Instructor: Ben Benjamin, Ph.D. Instructor: Ben Benjamin, Ph.D. [email protected] 1 SPONSOREDSPONSORED BY:BY: Over 30 years of experience building the finest portable treatment tables and accessories. Products that are visually stimulating, ergonomically supportive, and incredibly comfortable. The superior design and engineering capabilities merge to create the ultimate experience for you and your clients. www.oakworks.com 717.235.6807 SPONSOREDSPONSORED BY:BY: Mattes chair Side-lying position system Webinar Goal Explore the assessment and treatment of supraspinous ligament injuries: • Supraspinous ligaments L1-L5 • Suprasacral ligaments 2 Pretest 1. The supraspinous ligament is also known as the supraspinal ligament. True or False? 2. The suprasacral ligament connects the sacrum to the ilium. True or False? 3. The interspinous ligament is not continuous from vertebra to vertebra; it only connects two spinous processes to each other. True or False? 4. The supraspinous ligament in the low back limits lumbar flexion. True or False? 5. The posterior layer of thoracolumbar fascia and multifidus muscles combine to form the lumbar supraspinous ligaments. True or False? 6. The suprasacral ligament holds the sacrum to the pelvis. True or False? Anatomy Anatomy of the Supraspinous Ligaments • Connect all five lumbar vertebrae • Connect L5 to the sacrum • Sometimes called the supraspinal ligaments 3 Anatomy of the Supraspinous Ligaments • Run between the tips of the spinous
    [Show full text]
  • Development, Validation and Clinical Application of Finite Element Human Pelvis Model
    Health Science Campus FINAL APPROVAL OF THESIS Master of Science in Biomedical Sciences Development, validation and clinical application of finite element human pelvis model Submitted by: Alexander A. Ivanov In partial fulfillment of the requirements for the degree of Master of Science in Biomedical Sciences Examination Committee Signature/Date Major Advisor: Nabil Ebraheim, M.D. Academic Vijay Goel, Ph.D. Advisory Committee: Ashok Biyani, M.D. Senior Associate Dean College of Graduate Studies Michael S. Bisesi, Ph.D. Date of Defense: May 15, 2008 A Thesis Entitled Development, Validation and Clinical Application of the Finite Element Model of Human Pelvis. By Alexander A. Ivanov, M.D. Submitted as partial fulfillment of the requirements for the Master of Science in Orthopaedic Science ______________________________ Advisor: Dr. Nabil A. Ebraheim, M.D. ______________________________ Co-Advisor: Dr. Vijay K. Goel, Ph.D. ______________________________ Graduate School The University of Toledo 2008 1 © 2008, Alexander A. Ivanov 2 College of Health Science I HEREBY RECOMMEND THAT THE THESIS PREPARED UNDER MY SUPERVISION BY: Alexander A Ivanov, M.D. ENTITLED: Development, validation and clinical application of finite element human pelvis model BE ACCEPTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF: Master of Science in Orthopaedic Science ______________________________________________________________ Thesis Advisor: Dr. Nabil A. Ebraheim, M.D. _______________________________________________________________ Thesis Co-Advisor: Dr. Vijay K. Goel, Ph.D. Recommendation concurred by: ___________________________________ Committee Dr.Ashok Biyani, M.D. Of Final Examination ________________________________________________________________ Dean, College of Health Science 3 Acknowledgment I would like to extend my gratitude to my advisors Dr. Nabil Ebraheim and Dr. Vijay Goel for their incredible support of this work.
    [Show full text]
  • A Case-Based Review
    NEUROSURGICAL FOCUS Neurosurg Focus 38 (4):E3, 2015 Magnetic resonance imaging of traumatic injury to the craniovertebral junction: a case-based review Anil K. Roy, MD,1 Brandon A. Miller, MD, PhD,1 Christopher M. Holland, MD, PhD,1 Arthur J. Fountain Jr., MD,2 Gustavo Pradilla, MD,1 and Faiz U. Ahmad, MD1 Departments of 1Neurosurgery and 2Radiology, Emory University School of Medicine, Atlanta, Georgia OBJECT The craniovertebral junction (CVJ) is unique in the spinal column regarding the degree of multiplanar mobility allowed by its bony articulations. A network of ligamentous attachments provides stability to this junction. Although liga- mentous injury can be inferred on CT scans through the utilization of craniometric measurements, the disruption of these ligaments can only be visualized directly with MRI. Here, the authors review the current literature on MRI evaluation of the CVJ following trauma and present several illustrative cases to highlight the utility and limitations of craniometric mea- sures in the context of ligamentous injury at the CVJ. METHODS A retrospective case review was conducted to identify patients with cervical spine trauma who underwent cervical MRI and subsequently required occipitocervical or atlantoaxial fusion. Craniometric measurements were per- formed on the CT images in these cases. An extensive PubMed/MEDLINE literature search was conducted to identify publications regarding the use of MRI in the evaluation of patients with CVJ trauma. RESULTS The authors identified 8 cases in which cervical MRI was performed prior to operative stabilization of the CVJ. Craniometric measures did not reliably rule out ligamentous injury, and there was significant heterogeneity in the reliability of different craniometric measurements.
    [Show full text]