4 Linear Power Amplifiers
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Chapter 2 Basic Concepts in RF Design
Chapter 2 Basic Concepts in RF Design 1 Sections to be covered • 2.1 General Considerations • 2.2 Effects of Nonlinearity • 2.3 Noise • 2.4 Sensitivity and Dynamic Range • 2.5 Passive Impedance Transformation 2 Chapter Outline Nonlinearity Noise Impedance Harmonic Distortion Transformation Compression Noise Spectrum Intermodulation Device Noise Series-Parallel Noise in Circuits Conversion Matching Networks 3 The Big Picture: Generic RF Transceiver Overall transceiver Signals are upconverted/downconverted at TX/RX, by an oscillator controlled by a Frequency Synthesizer. 4 General Considerations: Units in RF Design Voltage gain: rms value Power gain: These two quantities are equal (in dB) only if the input and output impedance are equal. Example: an amplifier having an input resistance of R0 (e.g., 50 Ω) and driving a load resistance of R0 : 5 where Vout and Vin are rms value. General Considerations: Units in RF Design “dBm” The absolute signal levels are often expressed in dBm (not in watts or volts); Used for power quantities, the unit dBm refers to “dB’s above 1mW”. To express the signal power, Psig, in dBm, we write 6 Example of Units in RF An amplifier senses a sinusoidal signal and delivers a power of 0 dBm to a load resistance of 50 Ω. Determine the peak-to-peak voltage swing across the load. Solution: a sinusoid signal having a peak-to-peak amplitude of Vpp an rms value of Vpp/(2√2), 0dBm is equivalent to 1mW, where RL= 50 Ω thus, 7 Example of Units in RF A GSM receiver senses a narrowband (modulated) signal having a level of -100 dBm. -

Wideband Automatic Gain Control Design in 130 Nm CMOS Process for Wireless Receiver Applications
Wideband Automatic Gain Control Design in 130 nm CMOS Process for Wireless Receiver Applications A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science in Engineering By Joseph Benito Strzelecki, B.S. Wright State University, 2013 2015 Wright State University WRIGHT STATE UNIVERSITY GRADUATE SCHOOL _August 19, 2015_______ I HEREBY RECOMMEND THAT THE THESIS PREPARED UNDER MY SUPERVISION BY Joseph Benito Strzelecki ENTITLED Wideband Automatic Gain Control Design in 130 nm CMOS Process for Wireless Receiver Applications BE ACCEPTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF Master of Science in Engineering. ___________________________________ Saiyu Ren, Ph.D. Thesis Director ___________________________________ Brian D. Rigling, Ph.D. Department Chair Committee on Final Examination ________________________________ Saiyu Ren, Ph.D. ________________________________ Raymond E. Siferd, Ph.D. ________________________________ John M. Emmert, Ph.D. ________________________________ Arnab K. Shaw, Ph.D. ________________________________ Robert E. W. Fyffe, Ph.D. Vice President for Research and Dean of the Graduate School Abstract Strzelecki, Joseph Benito, M.S.Egr, Department of Electrical Engineering, Wright State University, 2015. “Wideband Automatic Gain Control Design in 130 nm CMOS Process for Wireless Receiver Applications” An analog automatic gain control circuit (AGC) and mixer were implemented in 130 nm CMOS technology. The proposed AGC was intended for implementation into a wireless receiver chain. Design specifications required a 60 dB tuning range on the output of the AGC, a settling time within several microseconds, and minimum circuit complexity to reduce area usage and power consumption. Desired AGC functionality was achieved through the use of four nonlinear variable gain amplifiers (VGAs) and a single LC filter in the forward path of the circuit and a control loop containing an RMS power detector, a multistage comparator, and a charging capacitor. -

An Overview of Automatic Level Control
Maxim > Design Support > Technical Documents > Application Notes > Audio Circuits > APP 3673 Keywords: MAX9756, ALC, Automatic Level Control, AGC, Automatic Gain Control, Maxim APPLICATION NOTE 3673 An Overview of Automatic Level Control Dec 22, 2005 Abstract: Automatic Level Control (ALC) is a technology that automatically controls output power to the speaker. ALC prevents loudspeaker overload and optimizes dynamic range. This application note presents ALC technology and demonstrates its use in the MAX9756/MAX9757/MAX9758 stereo speaker amplifiers. Maxim's Automatic Level Control (ALC) offers two key benefits (Figures 1 and 2). 1. It protects the loudspeaker by limiting the amplifier output power. 2. It boosts low-level signals without distorting the high-level signals. ALC is implemented in the MAX9756, MAX9757, and MAX9758 2.3W stereo speaker amplifiers and DirectDrive headphone amplifiers. Attend this brief webcast by Maxim on TechOnline Figures 1 and 2. The MAX9756's automatic level control (ALC) function protects the speakers without adding distortion. ALC vs. Output Limiting ALC differs from traditional output limiting. An output-limiter function limits the output swing at a predetermined level so that the transducer is protected from overvoltage peaks. Clipping (distortion) is added Page 1 of 5 at the output signal as a result (Figure 3). An ALC function, however, reduces the gain so that the transducer is protected. No distortion is added (Figure 4). Figure 3. The output limiter clips the output signal in overvoltage conditions and, thus, produces audible distortion. Figure 4. The MAX9756's ALC reduces the amplifier gain in overvoltage conditions so that no distortion is added to the output signal. -

UNIVERSITY of CALIFORNIA Los Angeles Wideband Reconfigurable Blocker Tolerant Receiver for Cognitive Radio Applications a Disser
UNIVERSITY OF CALIFORNIA Los Angeles Wideband Reconfigurable Blocker Tolerant Receiver for Cognitive Radio Applications A dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in Electrical Engineering by Qaiser Nehal 2018 c Copyright by Qaiser Nehal 2018 ABSTRACT OF THE DISSERTATION Wideband Reconfigurable Blocker Tolerant Receiver for Cognitive Radio Applications by Qaiser Nehal Doctor of Philosophy in Electrical Engineering University of California, Los Angeles, 2018 Professor Asad A. Abidi, Chair Cognitive radios (CRs) use \white spaces" in spectrum for communication. This requires front-end circuits that are highly linear when the white space is adjacent to a strong blocker. For example, in the TV spectrum (54 MHz-862 MHz) broadcast transmissions are the block- ers. This work describes the design of a wideband blocker tolerant receiver. First EKV based MOSFET model is used to analyze RF transconductor distortion. Expressions for its IIP3 and P1dB are also given. Derivative superposition based linearization scheme for the RF transconductor is also explained. Second mixer switch nonlinearity is analyzed using EKV. Simple expressions for receiver IIP3 and P1dB are given that provide design insights for linearity optimization. Low phase noise LO design is also described to lower receiver noise figure in the presence of large blockers. Finally, transimpedance amplifier (TIA) large-signal operation is studied using EKV. It is shown that source follower inverter-based TIA transconductor results in higher receiver P1dB. A prototype receiver based on these ideas was designed in 16nm FinFET CMOS. Mea- sured results show that receiver can operate from 100 MHz to 6 GHz and can tolerate up to +12 dBm blockers. -

Gan Essentials™
APPLICATION NOTE AN-010 GaN Essentials™ AN-010: GaN for LDMOS Users NITRONEX CORPORATION 1 JUNE 2008 APPLICATION NOTE AN-010 GaN Essentials: GaN for LDMOS Users 1. Table of Contents 1. TABLE OF CONTENTS................................................................................................................................... 2 2. ABSTRACT......................................................................................................................................................... 3 IMPEDANCE PROFILES.......................................................................................................................................... 3 2.1. INPUT IMPEDANCE .................................................................................................................................... 3 2.2. OUTPUT IMPEDANCE ................................................................................................................................ 4 3. STABILITY ......................................................................................................................................................... 5 4. CAPACITANCE VS. VOLTAGE ................................................................................................................... 6 4.1. TYPICAL CAPACITANCE -VOLTAGE (CV) CHARACTERISTICS ................................................................ 6 4.2. OUTPUT CAPACITANCE COMPARISON BETWEEN GAN AND LDMOS .................................................. 7 5. BIAS CIRCUITS................................................................................................................................................ -

Replacing the Automatic Gain Control Loop in a Mobile, Digital TV Broadcast Receiver by a Software Based Solution
Replacing the automatic gain control loop in a mobile, digital TV broadcast receiver by a software based solution diploma thesis Patrick Boettcher Technische Fachhochschule Wildau Fachbereich Betriebswirtschaft/Wirtschaftsinformatik Date: 09.03.2008 Erstbetreuer: Prof. Dr. Christian Müller Zweitbetreuer: Prof. Dr. Bernd Eylert ii A part of this diploma thesis is not available until April 2010, because it is protected by a lock flag. The complete work can and will be made available by that time. The parts affected are – Chapter 4, – Chapter 5, – Appendix C and – Appendix D. If by that time you cannot find the complete work anywhere, please contact the author. iii Danksagung An dieser Stelle möchte ich all jenen danken, die durch ihre fachliche und persönliche Unterstützung zum Gelingen dieser Diplomarbeit beigetragen haben. Besonderer Dank gebührt meiner Lebenspartnerin Ariane und meinen Eltern, die mir dieses Studium durch ihre Unterstützung ermöglicht haben und mir fortwährend Vorbild und Ansporn waren. Weiterhin bedanke ich mich bei Professor Dr. Christian Müller und Professor Dr. Bernd Eylert für die Betreuung dieser Diplomarbeit. Großer Dank gilt ebenfalls meinen Kollegen bei DiBcom S.A., die mir die Möglichkeit gaben, diese Arbeit zu verfassen und mich technich sehr stark unterstützten. Vor allem möchte ich mich in diesem Zusammenhang bei Jean-Philippe Sibers bedanken, der mir immer mit einer Inspriration zur Seite stand. Gleiches gilt für das „Physical Layer Software Team“: Luc Banda, Frédéric Tarral und Vincent Recrosio. Acknowledgment I want to use this opportunity to thank everyone who supported me personally and professionally to create this diploma thesis. Special thanks appertain to my partner Ariane and my parents, who supported me during my studies and who continuously guided and motivated me. -
Next Topic: NOISE
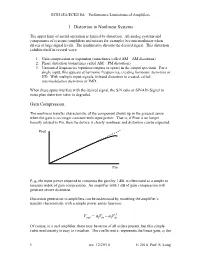
ECE145A/ECE218A Performance Limitations of Amplifiers 1. Distortion in Nonlinear Systems The upper limit of useful operation is limited by distortion. All analog systems and components of systems (amplifiers and mixers for example) become nonlinear when driven at large signal levels. The nonlinearity distorts the desired signal. This distortion exhibits itself in several ways: 1. Gain compression or expansion (sometimes called AM – AM distortion) 2. Phase distortion (sometimes called AM – PM distortion) 3. Unwanted frequencies (spurious outputs or spurs) in the output spectrum. For a single input, this appears at harmonic frequencies, creating harmonic distortion or HD. With multiple input signals, in-band distortion is created, called intermodulation distortion or IMD. When these spurs interfere with the desired signal, the S/N ratio or SINAD (Signal to noise plus distortion ratio) is degraded. Gain Compression. The nonlinear transfer characteristic of the component shows up in the grossest sense when the gain is no longer constant with input power. That is, if Pout is no longer linearly related to Pin, then the device is clearly nonlinear and distortion can be expected. Pout Pin P1dB, the input power required to compress the gain by 1 dB, is often used as a simple to measure index of gain compression. An amplifier with 1 dB of gain compression will generate severe distortion. Distortion generation in amplifiers can be understood by modeling the amplifier’s transfer characteristic with a simple power series function: 3 VaVaVout=−13 in in Of course, in a real amplifier, there may be terms of all orders present, but this simple cubic nonlinearity is easy to visualize. -

5 Steps to Selecting the Right RF Power Amplifier
modular rf 5 Steps to Selecting the Right RF Power Amplifier Jason Kovatch Sr. Development Engineer AR Modular RF, Bothell WA You need an RF power amplifier. You have measured the power of your signal and it is not enough. You may even have decided on a power level in Watts that you think will meet your needs. Are you ready to shop for an amplifier of that wattage? With so many variations in price, size, and efficiency for amplifiers that are all rated at the same number of Watts many RF amplifier purchasers are unhappy with their selection. Some of the unfortunate results of amplifier selection by Watts include: unacceptable distortion or interference, insufficient gain, premature amplifier failure, and wasted money. Following these 5 steps will help you avoid these mistakes. Step 1 - Know Your Signal Step 2 – Do the Math Step 3 - Window Shopping Step 4 - Compare Apples to Apples Step 5 – Shopping for Bells and Whistles Step 1 – Know Your Signal You need to know 2 things about your signal: what type of modulation is on the signal and the actual Peak power of your signal to be amplified. Knowing the modulation is the most important as it defines broad variations in amplifiers that will provide acceptable performance. Knowing the Peak power of your signal will allow you calculate your gain and/or power requirements, as shown in later steps. Signal Modulation and Power- CW, SSB, FM, and PM are Easy To avoid distortion, amplifiers need to be able to faithfully process your signal’s peak power. -

Large Signal RF Power Transmission Characterization of Ingap HBT for RF Power Amplifiers
Vol. 31, No. 1 Journal of Semiconductors January 2010 Large signal RF power transmission characterization of InGaP HBT for RF power amplifiers Zhao Lixin(赵立新), Jin Zhi(金智), and Liu Xinyu(刘新宇) (Institute of Microelectronics, Chinese Academy of Sciences, Beijing 100029, China) Abstract: The large signal RF power transmission characteristics of an advanced InGaP HBT in an RF power amplifier are investigated and analyzed experimentally. The realistic RF powers reflected by the transistor, transmitted from the transistor and reflected by the load are investigated at small signal and large signal levels. The RF power multiple frequency components at the input and output ports are investigated at small signal and large signal levels, including their effects on RF power gain compression and nonlinearity. The results show that the RF power reflections are different between the output and input ports. At the input port the reflected power is not always proportional to input power level; at large power levels the reflected power becomes more serious than that at small signal levels, and there is a knee point at large power levels. The results also show the effects of the power multiple frequency components on RF amplification. Key words: large signal characteristics; InGaP HBT; nonlinearity DOI: 10.1088/1674-4926/31/1/014001 PACC: 7280E; 7360L 1. Introduction nonlinear vector network analyzer systemŒ9; 10, and for maxi- mum output power at initial bias conditions of VCE = 3.61 V, Advanced indium gallium phosphide heterojunction bipo- IC = 53.7 mA, VBE = 1.28 V, IB = 0.71 mA. lar transistors (InGaP HBTs) are key components in RF power With the injection of a sinusoidal RF signal and increas- Œ1 3 amplifiers in radar and communication systems . -

Amplifiers
ECE 451 Advanced Microwave Measurements Amplifier Characterization Jose E. Schutt-Aine Electrical & Computer Engineering University of Illinois [email protected] ECE 451 – Jose Schutt-Aine 1 Transistor Technology Transistors are semiconductor devices with 3 terminals. They are used to amplify signals and get voltage, current or power gain • Tree fundamental types – Bipolar junction transistors (BJT) – Junction field effect transistors (JFET) – Metal-oxide semiconductor transistors (MOSFET) • Technologies – Silicon – Compound Semiconductors (GaAs, InP, GaN) ECE 451 – Jose Schutt-Aine 2 Models for Transistors • Polarity – NPN, PNP for BJT – NMOS, PMOS for MOSFET – CMOS NPN is favorites for BJT NMOS is favorite for MOSFET drain collector C base gate B E emitter source NPN NMOS ECE 451 – Jose Schutt-Aine 3 Transistor Models • Bipolar – Ebers-Moll – Gummel-Poon • MOSFET – Shichman-Hodges – BSIM ECE 451 – Jose Schutt-Aine 4 MOSFET Amplifier Common Source Topology Small‐Signal Model ECE 451 – Jose Schutt-Aine 5 BJT Amplifier Common Emitter Topology Small‐Signal Model ECE 451 – Jose Schutt-Aine 6 Amplifier Efficiency PRF, out Total PPDCRFin , PP A RF,, out RF in PAE P AB DC B C ECE 451 – Jose Schutt-Aine 7 Amplifier Efficiency For high‐gain amplifiers, PRF,in << PDC and PRF, out Total PAE PDC Efficiencies are typically between 25% and 50% • Class A amplifier – Maintain bias so that the transistor is in the middle of the linear range – Efficiency is reduced because of DC current – Best linearity – Choice for small signal (small input) amplification ECE 451 – Jose Schutt-Aine 8 Amplifier Efficiency Efficiency is improved by reducing DC power and moving bias point further down the DC load line as in class B, AB and C. -

RF Measurements Techniques
Fritz Caspers Piotr Kowina Manfred Wendt 2015 The CERN Accelerator School Advanced Accelerator Physics Instructions NCBJ - Świerk National Centre for Nuclear Research Warsaw - Poland 27 September - 9 October 2015 RF Measurements Techniques Suggested measurements – overview Spectrum Analyzer test stand 1 © Measurements of several types of modulation (AM FM PM) in the time and frequency domain. © Superposition of AM and FM spectrum (unequal carrier side bands). © Concept of a spectrum analyzer: the superheterodyne method. Practice all the different settings (video bandwidth, resolution bandwidth etc.). Advantage of FFT spectrum analyzers. Spectrum Analyzer test stand 2 © Measurement of the TOI point of some amplifier (intermodulation tests). © Concept of noise figure and noise temperature measurements, testing a noise diode, the basics of thermal noise. © EMC measurements (e.g.: analyze your cell phone spectrum). © Nonlinear distortion in general concept and application of vector spectrum analyzers, spectrogram mode. © Measurement of the RF characteristic of a microwave detector diode (output voltage versus input power... transition between regime output voltage proportional input power and output voltage proportional input voltage). Spectrum Analyzer test stand 3 © Concept of noise figure and noise temperature measurements, testing a noise diode, the basics of thermal noise. © Noise figure measurements on amplifiers and also attenuators. © The concept and meaning of ENR numbers. © Noise temperature of the fluorescent tubes in the room using a satellite receiver Network Analyzer test stand 1 © Calibration of the Vector Network Analyzer. © Navigation in the Smith Chart. © Application of the triple stub tuner for matching. © Measurements of the light velocity using a trombone (constant impedance adjustable coax line) in the frequency domain. -

Chapter 2 Power Control and Linear Transmitter Fundamental Theory
Chapter 2 Power Control and Linear Transmitter Fundamental Theory 2.1 Typical power control architecture The digital wireless communications standard requires accurate control of a unit`s transmitted power over a wide dynamic range. Accurate power control is required to meet system specifications under operating conditions like supply voltage variation. Today, The most common solution today is a power-control loop based on a directional coupler with a peak detector and a comparator. 2.1.1 RF attenuator power control architecture With RF attenuator power control, the attenuator is inserted into two stages (is shown in Figure 2.1) before the power amplifier. Figure.2.2 shows the RF attenuator. Figure 2.1 RF attenuator power control 3 Figure 2.2 A four diode attenuator This decreasing the RF power into the power transistors, hence reducing the RF output power, as long as the amplifier is not driven into saturation. The output power in the RF attenuator control is related to the linear attenuation of input power. The fact that there is a simple linear relation between control signal and RF output power provides three disadvantages: 1. It is too small that the dynamic range of the RF attenuator is 20 dB. 2. The diode is saturated when large signal into the pin diode of RF attenuator. 3. The mismatch between the two stages is caused by the reflecting attenuator. 2.1.2 A variable gain of pre-amplifier power control architecture The amplifier is designed to a variable gain device. Figure2.3 shows the architecture. The different gain control is based on a attenuation relation between the power of the amplifier.