Chapter 2 Basic Concepts in RF Design
1 Sections to be covered
• 2.1 General Considerations • 2.2 Effects of Nonlinearity • 2.3 Noise • 2.4 Sensitivity and Dynamic Range • 2.5 Passive Impedance Transformation
2 Chapter Outline
Nonlinearity Noise Impedance Harmonic Distortion Transformation Compression Noise Spectrum Intermodulation Device Noise Series-Parallel Noise in Circuits Conversion Matching Networks
3 The Big Picture: Generic RF Transceiver Overall transceiver
Signals are upconverted/downconverted at TX/RX, by an oscillator controlled by a Frequency Synthesizer. 4 General Considerations: Units in RF Design
Voltage gain: rms value
Power gain: These two quantities are equal (in dB) only if the input and output impedance are equal. Example： an amplifier having an input resistance of R0 (e.g., 50 Ω) and driving a load resistance of R0 :
5 where Vout and Vin are rms value. General Considerations: Units in RF Design
“dBm”
The absolute signal levels are often expressed in dBm (not in watts or volts);
Used for power quantities, the unit dBm refers to “dB’s above 1mW”.
To express the signal power, Psig, in dBm, we write
6 Example of Units in RF
An amplifier senses a sinusoidal signal and delivers a power of 0 dBm to a load resistance of 50 Ω. Determine the peak-to-peak voltage swing across the load.
Solution:
a sinusoid signal having a peak-to-peak amplitude of Vpp an rms value of Vpp/(2√2), 0dBm is equivalent to 1mW,
where RL= 50 Ω thus,
7 Example of Units in RF A GSM receiver senses a narrowband (modulated) signal having a level of -100 dBm. If the front-end amplifier provides a voltage gain of 15 dB, calculate the peak-to-peak voltage swing at the output of the amplifier.
Solution: suppose the input and output impedance are equal.
convert the received signal level to voltage: -100 dBm is 100 dB below 632 mVpp. 100 dB for voltage quantities is equivalent to 105.
-100 dBm is equivalent to 6.32 μVpp. This input level is amplified by 15 dB (≈ 5.62),
The output swing is 35.5 μVpp.
Notice: For a narrowband (not sinusoid) 0-dBm signal, it is still possible to approximate the (average) peak-to-peak swing as 632mV. 8 Voltage vs Power Why the output voltage of the amplifier is of interest in this example? – If the circuit following the amplifier does not present a 50-Ω input impedance, the power gain and voltage gain are not equal in dB.
– Mostly, the next stage may exhibit a purely capacitive input impedance, thereby requiring no signal “power”.
• one stage drives the gate of the transistor in the next stage.
9 dBm Used at Interfaces Without Power Transfer We use “dBm” at interfaces that do not necessarily entail power transfer. (a) LNA driving a pure-capacitive
impedance with a 632-mVpp swing, delivering no average power. How about the power delivery?
Assumption: attaching an ideal voltage buffer to node X and drive a 50-Ω load. the signal at node X has a level of 0 dBm, means that if this signal were applied to a 50-Ω load, then it would deliver 1 mW.
(b) Use of fictitious buffer to visualize the signal level in “dBm” voltage buffer 10 General Considerations: linearity
A system is linear if its output can be expressed as a linear combination (superposition) of responses to individual inputs.
For arbitrary a and b, it holds that:
Any system that does not satisfy this condition is nonlinear. Example:
nonzero initial conditions or dc offsets cause nonlinearity;
However, we often relax the rule ------accommodate these two effects.
11 Nonlinearity: Memoryless and Static System
Memoryless or static : if its output does not depend on the past values of its input;
Memoryless, linear
The input/output characteristic of a memoryless nonlinear system can be approximated with a polynomial
Memoryless, nonlinear
If the system is time variant，αj would be general functions of time. 12 Nonlinearity: Memoryless and Static System
Example of a memoryless nonlinear circuit:
If M1 operates in the saturation region and can be approximated as a square-law device [Lee]
1 = 2 then 𝑊𝑊 2 𝐼𝐼𝐷𝐷 𝜇𝜇𝑛𝑛𝐶𝐶𝑜𝑜𝑜𝑜 𝑉𝑉𝑖𝑖𝑖𝑖 − 𝑉𝑉𝑇𝑇𝑇𝑇 𝐿𝐿 Common-source stage
In this idealized case, the circuit displays only second-order nonlinearity.
13 Nonlinearity: Odd symmetry
A system has “odd symmetry” if y(t) is an odd function of x(t), i.e., if the response to –x(t) is the negative of that to x(t).
23 yt()=+++αα01 xt () α 2 x () t α 3 x () t +
y(t) is odd symmetry if αj=0 for even j.
Such a system is sometimes called “balanced”, as exemplified by the differential pair shown in the next page.
14 Example of Polynomial Approximation
For square-law MOS transistors operating in saturation, the characteristic “differential pair circuit” can be expressed as
If the differential input is small, approximate the characteristic by a polynomial.
Assuming
Approximation (Taylor Expansions) gives us:
Differential pair Input/output characteristic
15 Example of Polynomial Approximation
Observations
The first term represents linear operation,
the small-signal voltage gain of the circuit (-gmRD);
Due to symmetry, even-order nonlinear terms are absent;
Notice: square-law devices yield a third-order characteristic in this case.
16 General Considerations: Time Variance
A system is time-invariant if a time shift in its input results in the same time shift in its output.
If y(t) = f [x(t)]
then y(t-τ) = f [x(t-τ)]
Time Variance Nonlinearity
Do not be confused by these two attributes.
17 Example of Time Variance Plot the output waveform of the circuit in Fig. 1: vin1 = A1 cos ω1t vin2 = A2 cos(1.25ω1t ) Solution:
Fig.1
Switch: vout tracks vin2 if vin1 > 0 and is pulled down to zero by R1 if vin1 < 0.
vout is equal to the product of vin2 and a square wave toggling between 0 and 1.
This is an example of RF “mixers”. 18 A time shift in input does not result in the same time shift in output. Time Variance: Generation of Other Frequency Components S(t) denotes a square wave toggling between 0 and 1 with a frequency of
f1=ω1/(2π)
The spectrum of square wave: a train of impulses whose amplitude follow a sinc envelop. Illustration: T1= 2π /ω1
Multiplication in time domain
Convolution in frequency domain
A linear system can generate frequency components that do not exist in the19 input signal when system is time variant. Effects of nonlinearity
• ? Frequency • ? Amplitude • Harmonic distortion (谐波失真) • Gain compression (增益压缩) • Cross modulation (互调) • Intermodulation (交叉调制)
20 Notice
Analog and RF circuits can be approximated with a linear model for small-signal operation.
In general, we have
memoryless time-variant systems with input/output characteristic :
23 yt()≈+αα12 xt () x () t + α 3 x () t
α1 is considered as the small-signal gain.
The nonlinearity effects primarily arise from the third-order term α3.
21 Effects of nonlinearity
• Harmonic distortion (谐波失真) • Gain compression (增益压缩) • Cross modulation (互调) • Intermodulation (交叉调制)
22 Effects of Nonlinearity: Harmonic Distortion If a sinusoid is applied to a nonlinear system: the output exhibits frequency components that are integer multiplies (“harmonics”) of the input frequency. input: xt( )= A cosω t 23 output: yt()≈+αα12 xt () x () t + α 3 x () t
DC Fundamental Second Third Harmonic Harmonic
Arising from The term with the second-order input frequency nonlinearity 23 Observations
23 yt()≈+αα12 xt () x () t + α 3 x () t
Even-order harmonics result from αj with even j and vanish if the system has odd symmetry, If mismatches corrupt the symmetry, what will happen?
The amplitude of the nth harmonic grows in proportion to? An .
24 Example of Harmonic Distortion in Mixer
An analog multiplier “mixes” its two inputs, producing y(t) = kx1(t)x2(t), where k is a constant. Assume x1(t) = A1 cos ω1t and x2(t) = A2 cos ω2t. Question: (a) If the mixer is ideal, determine the output frequency components.
Solution:
(a)
Analog multiplier
The output contains the sum and difference frequencies.
These are “desired” components. 25 Example of Harmonic Distortion in Mixer
An analog multiplier “mixes” its two inputs below, producing y(t) = kx1(t)x2(t), where k is a constant. Assume x1(t) = A1 cos ω1t and x2(t) = A2 cos ω2t. (a)If the mixer is ideal, determine the output frequency components. (b) If the input port sensing x2(t) suffers from third-order nonlinearity, determine the output frequency components.
Solution:
(b) Third Harmonic of x2(t)
Analog multiplier
The mixers produces two “spurious” components at ω1+3ω2 and ω1-3ω2, Cause other problems… 26 These are “undesired” components that are difficult to remove by filter. Example of Harmonics on GSM Signal The transmitter in a 900-MHz GSM cellphone delivers 1 W of power to the antenna. Explain the effect of the harmonics of this signal.
The second harmonic? falls within another GSM cellphone band around 1800 MHz; Must be sufficiently small to impact the other users in that band.
The third, fourth, and fifth harmonics? do not coincide with any popular bands; but must still remain below a certain level imposed by regulatory organizations in each country. (中国工信部无线电管理局/US FCC)
The sixth harmonic? falls in the 5-GHz band used in wireless local area networks (WLANs).
fundamental
27 Effects of nonlinearity
• Harmonic distortion (谐波) • Gain compression (增益压缩) • Cross modulation (互调) • Intermodulation (交叉调制)
28 Gain Compression– Sign of α1, α3 = ω 23 xt( ) A cos t yt()≈+αα12 xt () x () t + α 3 x () t
2 The gain of fundamental component ω is equal to α1 + 3α3A /4 varied as A becomes larger.
Expansive: Compressive: 3 expanding the gain as the input The term α3x “bends” the characteristic amplitude increases for sufficiently large x, decreasing the gain as the input amplitude increases.
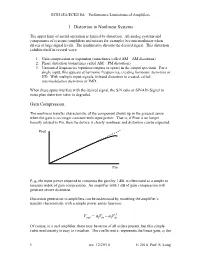
29 Most RF circuit of interest are compressive, we focus on this type. Gain Compression: 1-dB Compression Point
2 With α1α3 <0, the fundamental gain is equal to α1 + 3α3A /4 and falls as A rises.
1-dB compression point: defined as the input signal level that causes the small signal gain to drop by 1dB.
small signal gain
large signal gain
Plotted on a log-log scale as a function of the input level
Output level, Aout, falls below its ideal value by 1 dB at the 1-dB compression point, Ain,1dB. 30 Calculation
At the 1-dB compression point, Ain,1dB: 3 20log αα+=−A2 20log α 1dB 14 3in ,1dB 1
small signal gain
α1 Ain,1dB = 0.145 α3 large signal gain
Notice: The relationship of the input is between peak value (rather than the peak-to- peak value).
Ain and Aout are voltage quantities, but compression can also be expressed in31 terms of power quantities (dBm). Observations
• The 1-dB compression point is typically in the range of
-20 to -25 dBm (63.2 to 35.6 mVpp in 50-Ω system) at the input of RF receivers front-end amplifiers.
• We use the notations A1dB and P1dB interchangeably in this book.
• Why does compression matter? – a signal is so large as to reduce the gain of a receiver
32 Gain Compression: Effect on FM and AM Waveforms
Are they acceptable? FM signal carries no information in its amplitude and hence tolerates compression. √ AM contains information in its amplitude, hence distorted by compression. X
33 • Gain compression on two signals?
34 Gain Compression: Desensitization
If there are two signals: a small desired signal + a large interferer
According to the effect of gain compression, if a signal is too large, it will reduce the gain of a receiver.
Desensitization: when small desired signal is superimposed on the large interferer, the receiver gain is reduced even though the desired signal itself is small.
This phenomenon lowers the signal-to-noise ratio (SNR) at the receiver,35 even if the signal contains no amplitude information. Example of Gain Compression
A 900-MHz GSM transmitter delivers a power of 1 W to the antenna. By how much must the second harmonic of the signal be suppressed (filtered) so that it does not desensitize a 1.8-GHz receiver having P1dB = -25 dBm? Assume the receiver is 1 m away and the 1.8-GHz signal is attenuated by 10 dB as it propagates across this distance. Solution: The output power at 900 MHz is +30 dBm (1W).
With an attenuation of 10 dB, the second harmonic must not exceed -15 dBm at the transmitter antenna so that it is below P1dB of the receiver.
Thus, the second harmonic must remain at least 45 dB below the fundamental at the TX output.
In practice, this interference must be another several dB lower to ensure the 36 RX does not compress. How to quantify desensitization?
With the third-order characteristic,
23 yt()≈+αα12 xt () x () t + α 3 x () t
the output is:
For A1 << A2
2 The gain experienced by the desired signal is equal to α1 + 3α3A2 /2,
a decreasing function of A2 if α1α3 <0.
For sufficiently large A2, the gain drops to zero, and we say the signal is “blocked”. 37 Observations
In RF design, the term “blocking signal” or “blocker” refers to interferers that desensitize a circuit, even if they do not reduce the gain to zero.
Some RF receivers must be able to withstand blockers that are 60 to 70 dB greater than the desired signal.
38 Effects of nonlinearity
• Harmonic distortion (谐波) • Gain compression (增益压缩) • Cross modulation (互调) • Intermodulation (交叉调制)
39 Effects of Nonlinearity: Cross Modulation
When a weak signal and a strong interferer pass through a nonlinear system, “cross modulation” will happen.
Phenomenon: modulation (or noise) on the amplitude of the interferer will transfer to the amplitude of the weak signal.
40 Effects of Nonlinearity: Cross Modulation
Suppose that the interferer is an amplitude-modulated signal
where m is a constant and ωm denotes the modulating frequency.
For A1 << A2
41 Desired signal at output suffers from amplitude modulation at ωm and 2ωm. Example of Cross Modulation
Suppose an interferer contains phase modulation but not amplitude modulation. Does cross modulation occur in this case?
PM interferer (A2 is constant Solution: but Φ varies with time)
Expressing the input as:
We now note that ± (1) the second-order term yields components at ω1 ω2 but not at ω1------can be removed; 2 2 (2) the third-order term expansion gives 3α3A1 cos ω1t A2 cos (ω2t+Φ), according to cos2x=(1+cos2x)/2, results in a component at ω1.
42 The desired signal at ω1 does not experience cross modulation. (constant can be removed.) Example of Cross Modulation: observations
Phase-modulated interferers do not cause cross modulation in memoryless (static) nonlinear systems.
Cross modulation commonly arises in amplifiers that must simultaneously process many independent signal channels.
Examples include cable television transmitters and system employing “orthogonal frequency division multiplexing” (OFDM).
43 Effects of Nonlinearity: Intermodulation— Recall Previous Discussion
Desired Signal Harmonic distortion
Desired Signal + one (large) Desensitization + Cross Modulation interferer
Desired Signal + two large Intermodulation interferers???
44 Effects of Nonlinearity: Intermodulation
If two interferers at ω1 and ω2 are applied to a nonlinear system, – the output exhibits components that are not harmonics of these frequencies.
The phenomenon of “intermodulation” (IM) arises from “mixing” (multiplication) of the two components.
45 Effects of Nonlinearity: Intermodulation
Assume
23 Third-order characteristic, yt()≈+αα12 xt () x () t + α 3 x () t
Expanding the right-hand side and discarding the dc terms, ± Intermodulation products: harmonics, and components at ω1 ω2, we have:
Fundamental components:
46 Third-order IM products
The third-order IM products at 2ω1- ω2 and 2ω2-ω1 are of particular interest.
if ω1 and ω2 are close to each other,
2ω1- ω2 and 2ω2-ω1 are close to ω1 and ω2,
47 Intermodulation Product Falling on Desired Channel Interferer
desired
Suppose an antenna receives:
a small desired signal at ω0
two large interferers at ω1 and ω2, Applying to a low-noise amplifier (nonlinear). Suppose
The intermodulation product at 2ω1-ω2, falls onto the desired channel, corrupting the signal. 48 Example of Intermodulation
Suppose four Bluetooth users operate in a room as shown in figure below. User 4 is in the receive mode and attempts to sense a weak signal transmitted by User 1 at 2.410 GHz; Users 2 and 3 transmit at 2.420 GHz and 2.430 GHz, respectively. Explain what happens?
Solution:
The frequencies transmitted by Users 1, 2, and 3 are equally spaced; The intermodulation in the LNA of RX4 corrupts the desired signal at 2.410 GHz. 49 Example of Gain Compression and Intermodulation If the gain is not compressed, can we say that intermodulation is negligible? A Bluetooth receiver: a) a low-noise amplifier (LNA) having a gain of 10 b) input impedance of 50 Ω. The LNA senses a desired signal level of -80 dBm at 2.410 GHz and two interferers of equal levels at 2.420 GHz and 2.430 GHz. a) For simplicity, assume the LNA drives a 50-Ω load. a) Determine the value of α3 that yields a P1dB of -30 dBm. b) If each interferer is 10 dB below P1dB, determine the corruption experienced by the desired signal at the LNA output.
A = 0.145 αα -2 (a) From previous equation, in ,1dB 1 3 α3 = 14,500 V -80 dBm
(b) Each interferer has a level of -40 dBm (= 3.16 m Vp), the amplitude of the IM product at 2.410 GHz as:
(c) The desired signal is amplified by a factor of α1=10=20dB, emerging at the output at a level of -60dBm. 50 (d) The IM product is as large as the signal even though the LNA does not experience significant compression. Intermodulation: Third Intercept Point
“Third Intercept Point” (IP3): if the amplitude of each tone arises, that of the output IM products increases more sharply (∞A3). Thus, if we continue to raise A, the amplitude of the IM products eventually becomes equal to that of the fundamental tones at the output.
The input level at which this occurs is called the “input third interception point” (IIP3), where the corresponding output is represented by OIP3.
A: equal amplitude of each tone Equate the fundamental and IM amplitudes:
α1 A1dB = 0.145 α3
51 Example of Third Intercept Point A low-noise amplifier senses a -80-dBm signal at 2.410 GHz and two -20-dBm interferers at 2.420 GHz and 2.430 GHz. What IIP3 is required if the IM products must remain 20 dB below the signal? For simplicity, assume 50-Ω interfaces at the input and output.
Solution: IM amplitude Fundamental amplitude At the LNA output: >
>
Asig = 31.6μV; Aint = 31.6mV Extremely difficult to achieve in this case. > Usually we have:
A1dB: -20 to -25dBm > 3.16 VP +9.6dB 52 > +20dBm IP3: -10 to -15dBm Effects of Nonlinearity: Recall Previous Discussion So far we have discussed the case of:
Single Signal Harmonic distortion
Signal + one large interferer Desensitization + Cross Modulation
Signal + two large interferers Intermodulation
53 Effects of Nonlinearity: Cascaded Nonlinear Stages
Consider two nonlinear stages in cascade:
Considering only the first- and third-order terms, we have:
54 Cascaded Nonlinear Stages: Intuitive results
“ ” divide IP3 of the second stage by α1. Effect: the higher the gain of the first stage, the more nonlinearity is contributed by the second stage.
α1 ↑ → ↑ → ↑→ AIP3 ↓ → nonlinearity ↑ 55 IM Spectra in a Cascade
Most RF systems incorporate narrowband circuits ± the terms at ω1 ω2 , 2ω1, and 2ω2 are heavily attenuated at the output of the first stage second-order nonlinearity is attenuated.
For more stages:
Notice: The nonlinearity of the latter stages becomes increasingly more critical; because the IP3 of each stage is equivalently scaled down by the total gain preceding that stage. 56 Example of Cascaded Nonlinear Stages
A low-noise amplifier having an input IP3 of -10 dBm and a gain of 20 dB is followed by a mixer with an input IP3 of +4 dBm. Which stage limits the IP3 of the cascade more? Solution:
α1 = 20 dB
The scaled IP3 of the second stage AIP3,2 is lower than the IP3 of the first stage AIP3,1,
The second stage limits the overall IP3 more. 57 Sections to be covered
• 2.1 General Considerations • 2.2 Effects of Nonlinearity • 2.3 Noise • 2.4 Sensitivity • 2.5 Passive Impedance Transformation
58 Noise
The performance of RF systems is limited by noise.
Without noise, an RF receiver would be able to detect arbitrarily small inputs, allowing communication across arbitrarily long distances.
In this section, we review basic properties of noise and methods of calculating noise in circuits.
59 Noise: Noise as a Random Process “noise is random,” the instantaneous value of noise cannot be predicted. Example: a resistor tied to a battery and carrying a current. Due to the ambient temperature, each electron carrying the current experiences thermal agitation, moving toward the positive terminal of the battery with a random path;
Higher temperature
a) greater thermal agitation of electrons; b) larger fluctuations in the current.
The average current remains equal to VB/R; The instantaneous current displays random values. 60 Noise: Noise as a Random Process Noise cannot be characterized in terms of instantaneous voltages or currents.
How do we express the concept of larger random swings for a current or voltage quantity? Average power
n(t) represents the noise waveform
Noise components in circuits have a constant average power.
For example, Pn is known and constant for a resistor at a constant temperature.
61 Noise Spectrum: Power Spectral Density (PSD)
Total area under Sx(f) represents the average power carried by x(t)
Parseval's theorem
Two-Sided One-Sided
62 Example of Noise Spectrum
A resistor of value R1 generates a white noise voltage whose one-sided PSD is given by
Boltzmann constant k = 1.38 × 10-23 J/K The absolute temperature T.
(a) What is the total average power carried by the noise voltage? (b) What is the dimension of Sv(f)? (c) Calculate the noise voltage for a 50-Ω resistor in 1 Hz at room temperature.
， (a) Ideally, the area under Sv(f) appears to be infinite resistor noise arises from the finite ambient heat. In reality, Sv(f) begins to fall at f > 1 THz, exhibiting a finite total energy, i.e., thermal noise is not quite white.
2 (b) The dimension of Sv(f) is voltage squared per unit bandwidth (V /Hz), we may write the PSD as
where denotes the average power of Vn in 1 Hz.
(4kTRΔf) indicates the total noise in a bandwidth of Δf . 63 Example of Noise Spectrum
A resistor of value R1 generates a noise voltage whose one-sided PSD is given by
where k = 1.38 × 10-23 J/K denotes the Boltzmann constant and T the absolute temperature. (c) Calculate the noise voltage for a 50-Ω resistor in 1 Hz at room temperature.
(c) For a 50-Ω resistor at T = 270 C or 3000 K
a root-mean-squared (rms) quantity:
64 Noise Figure
How does the SNR degrade as the signal travels through a given circuit? If the circuit contains no noise, • the output SNR is equal to the input SNR • (even if the circuit acts as an attenuator.)
To quantify how noisy the circuit is, we define its noise figure (NF) as:
equal to 1 for a noiseless stage.
in decibels: 65 Device Noise
Model the noise by voltage and current sources:
Thermal noise of resistors can be modeled by a series voltage source with a PSD of [Thevenin equivalent, 戴维南等效] or a parallel current source with a PSD of 2 [Norton equivalent, 诺顿等效 ];
(a) (b) (a) Thevenin (b) Norton models of resistor thermal noise
Polarity of the sources is unimportant but must be kept same throughout the calculations. The choice of the model sometimes simplifies the analysis. 66 Noise in MOSFETS
Thermal noise of MOS transistors operating in the saturation region or can be modeled by a voltage is approximated by a current source in series with gate. source tied between the source and drain terminals;
(a) Current source (b) Voltage source
： γ is the “excess noise coefficient” and gm the transconductance. The value of γ 2/3 for long-channel transistors； may rise to even 2 in short-channel devices. The actual value of γ has other dependencies and is usually obtained by measurements for each generation of CMOS technology. 67 Other noises in MOSFETS Flicker or “1/f ” noise – Modeled by a voltage source in series with the gate,
– 1/f dependence
– For a given device size and bias current, the 1/f noise PSD intercepts the thermal noise PSD at some frequency, called the “1/f noise corner frequency,” fc.
– It can be negligible at high frequencies.
68 Effect of Transfer Function on Noise
If white noise is applied to a low-pass filter, how do we determine the PSD at the output?
If x(t) is applied to a linear, time-invariant system with a transfer function H(s), then the output spectrum is
where H(f)= H(s = j2πf ).
69 Example of Device Noise Sketch the PSD of the noise voltage measured across the parallel RLC tank depicted in figure below.
ZT
2 𝐼𝐼𝑛𝑛1
(a) RLC (b) inclusion of resistor noise (c) output noise spectrum due to R1
Modeling the noise of R1 by a current source ,
The transfer function Vn/In1 is equal to the impedance of the tank ZT ,
At f0, L1 and C1 resonate, reducing the circuit to only R1. Thus, the output noise at f0 is simply equal to 4kTR1. At lower or higher frequencies, the impedance of the tank falls ; 70 the output noise falls. Energy delivery of thermal noise What is the energy delivered by thermal noise?
R1 at room temperature; 0 R2 is an ideal noiseless resistance (at 0 K) ;
Effect: R1 continuous to draw thermal energy from its environment, converting it to noise and delivering the energy to R2.
The average power transferred to R2 is:
Transfer of noise from one resistor to another
This quantity reaches a maximum if R2 = R1 : PR2,max = kT (W/Hz) =-174 dBm/Hz
71 Available noise power Observations
• If a passive circuit dissipates energy, – it must contain a physical resistance – must produce thermal noise.
• “lossy circuits are noisy”.
72 A Theorem about Lossy Circuit
passive network
If the real part of the impedance seen between two terminals of a passive network is equal to Re{Zout},
the PSD of the thermal noise seen between these terminals is given by 4kTRe{Zout}
73 Lossy Circuit: example
(a) Transmitting antenna (b) receiving antenna producing thermal noise
A transmitter antenna As a receiving element, the dissipates energy by radiation antenna generates a thermal according to the equation noise PSD of 2 V TX,rms/Rrad,
where Rrad is the “radiation resistance”.
74 Useful Tools
• Effect of Transfer Function on Noise
• A Theorem about Lossy Circuit
passive network 75 Noise Figure
How does the SNR degrade as the signal travels through a given circuit? If the circuit contains no noise, • then the output SNR is equal to the input SNR • even if the circuit acts as an attenuator.
To quantify how noisy the circuit is, we define its noise figure (NF) as:
equal to 1 for a noiseless stage.
in decibels: 76 Noise Figure
Depends on: the circuit under consideration the SNR provided by the preceding stage.
If SNRin=∞ NF=∞ even though the circuit may have finite internal noise.
77 Calculation of Noise Figure (1)
A low-noise amplifier senses the signal received by an antenna;
The antenna “radiation resistance,” RS, produces thermal noise.
represents the thermal noise of the antenna;
represents the output noise of the LNA.
How to compute SNRin at the LNA input and SNRout at its output?
78 Calculation of Noise Figure (2)
If the LNA exhibits an input We assume a voltage gain of Av from the LNA input to the output; impedance of Zin, Both Vin and VRS experience an Output signal power: attenuation factor of α = Zin / (Zin + RS) Output noise consists of two parts: the noise of the antenna amplified by the LNA, the output noise of the LNA,
79 Calculation of Noise Figure (3)
Calculate the output noise due to the amplifier, divide it by the gain, 80 normalize it to 4kTRs , add 1 to the result. Calculation of Noise Figure (4)
Reduce the right hand side to a simpler form: The numerator is the total noise measured at the output, denoted as , includes both the source impedance noise and the LNA noise;
A0 =| α |Av is the voltage gain from Vin to Vout (not the gain from the LNA input to its output).
Divide total output noise by the gain from Vin to Vout
normalize the result to the noise of Rs 81 Noise Figure of Cascaded Stages
AP1 is the “available power gain” of the first stage, the “available power” at its output, Pout,av (the power that it would deliver to a matched load) divided by the available source power, PS,av (the power that the source would deliver to a matched load).
Called “Friis’ equation”, the noise contributed by each stage decreases as the total gain preceding that stage increases； the first few stages in a cascade are the most critical. 82 Noise Figure of Lossy Circuits
Passive circuits (filters) appear at the front end of RF transceivers; their loss proves critical. attenuate the signal introduce noise.
Proposition: the noise figure of a passive circuit is equal to its “power loss,” defined as L=Pin/Pout,
Pin is the available source power;
Pout is the available power at the output.
Proof: The lossy circuit is driven by a source impedance of RS while driving a load impedance of RL.
83 Noise Figure of Lossy Circuits
According to the theorem of “thermal noise model of lossy circuit”, we have
VThev
2 The available source power is Pin =V in/(4RS); Divide total output noise by the According to Thevenin equivalent, the squared gain from Vin to Vout and available (matching) output power is Pout normalize the result to the noise of Rs 2 =V Thev/(4Rout).
84 Example of Noise Figure of Lossy Circuits A receiver a front-end band-pass filter (BPF) to suppress some of the interferers that may desensitize the LNA; the filter has a loss of L; the LNA a noise figure of NFLNA; calculate the overall noise figure.
The noise figure of the filter is NFfilt,
Friis’ equation:
According to the definition of L, available power gain Ap1=1/L
where NFLNA can be calculated with respect to the output resistance of the filter Example: 85 if L = 1.5 dB and NFLNA = 2 dB, then NFtot = 3.5 dB. Sections to be covered
• 2.1 General Considerations • 2.2 Effects of Nonlinearity • 2.3 Noise • 2.4 Sensitivity • 2.5 Passive Impedance Transformation
86 Sensitivity The minimum signal level that a receiver can detect with “acceptable quality.” acceptable quality: sufficient signal-to-noise ratio, It depends on the type of modulation and the corruption (e.g., bit error rate) that the system can tolerate.
All quantities expressed in W/Hz (or dBm/Hz)
Match of receiver and antenna Eq. (2.91) PRS= kT= -174 dBm/Hz
Sensitivity Noise Floor: the total integrated noise87 Example of Sensitivity Compare the sensitivities of these two systems if both have an NF of 7 dB. A GSM receiver requires a minimum SNR of 12 dB and has a channel bandwidth of 200 kHz. A wireless LAN receiver specifies a minimum SNR of 23 dB and has a channel bandwidth of 20 MHz.
Solution:
For the GSM receiver, Psen = -174+7+53+12= -102 dBm,
For the wireless LAN system, Psen = -174+7+73+23= -71 dBm.
Does this mean that the latter is inferior? No, the latter employs a much wider bandwidth and a more efficient modulation to accommodate a data rate of 54 Mb/s.
The GSM system handles a data rate of only 270 kb/s.
In other words, specifying the sensitivity of a receiver without the data rate is not meaningful. 88 The journey of Noise
RF Receiver
Source Digital Receiver 89 Sections to be covered
• 2.1 General Considerations • 2.2 Effects of Nonlinearity • 2.3 Noise • 2.4 Sensitivity • 2.5 Passive Impedance Transformation – Thomas H. Lee – Razavi – 张肃文
90 Sections to be covered
• 2.1 General Considerations • 2.2 Effects of Nonlinearity • 2.3 Noise • 2.4 Sensitivity • 2.5 Passive Impedance Transformation – Series RLC tank – Parallel RLC tank – Series and parallel RC/RL networks – Basic Matching Networks
91 Series RLC tank circuit
The complex impedance of this circuit is given by adding up the impedance of the components:
1 ZRjXRjL=+=+()ω − ωC Resistance reactance 1 ZR=22 +−()ω L ωC 1 when ωL = ZRmin = V - the voltage of the power source ωC I - the current in the circuit R - the resistance of the resistor 1 resonance frequency: ωs = L - the inductance of the inductor LC C - the capacitance of the capacitor There is a valley in impedance at resonance. 1 L 92 Characteristic impedance: ρω=s L = = ωsCC Attributes of impedance Z Z 1 ZRjXRjL=+=+()ω − ωC
1 magnitude ZR=22 +−()ω L ωC
ω ωs ϕ
π 2 phase shift ω
ωs π − 2 93 Quality Factor
The quality factor, Q, indicates how close to ideal an energy-storing device is.
An ideal capacitor or inductor dissipates no energy, exhibiting an infinite Q, but a series resistance or a parallel resistance reduces its Q.
The definition of Q:
energy stored Q = ω Q is dimensionless. average power dissipated
As to a series RLC tank circuit:
1 ρ ωωLC1 L Q = =ss = = s R R R RC 94 Frequency response of the current: the magnitude
1 ZR=22 +−()ω L ωC I 11 = = Imax 22ω ωωs 2 1(+−Qs )1(+ Qs 2 ) ωωs ωs
ωωω= − s
Imax is the maximum current at resonance frequency
ωs 95 Frequency response of the current: the phase shift
1 X is the imaginary part of Z, defined as ZRjXRjL=+=+()ω − ωC reactance V − X I = ϕ = −tg 1 Z R ϕ π 2
ωs ω Q 2 QQ> Q1 12 π − 2 96 Bandwidth The resonance effect can be used for filtering;
The rapid change in impedance near resonance can be used to Pass signals block signals
A key parameter in filter design is bandwidth. The bandwidth is measured between the 3dB-points；
Half-power frequencies: the power passed through the circuit has fallen to half the value passed at resonance.
ωs B =−=ωω21 Qs
97 Q and Bandwidth B
• Q is related to bandwidth; – low Q circuits are wide band – high Q circuits are narrow band
• Q is the inverse of fractional bandwidth( B/ωs );
• Q factor is directly proportional to selectivity, as Q factor depends inversely on bandwidth.
ω Q = s s B
98 Loaded Q factor
L R C
R S
R L V s load
ωs L Qs = Unloaded Q RRs +
ωs L QQLs= < 99 RsL++ RR Parallel RLC tank circuit The complex admittance of this circuit is given by adding up the admittances of the components: 1 YGjC=+−()ω Iin R C L V ωL out Conductance susceptance
1 YG=22 +−()ω C ωL 1 1 when ωL = YG= = ωC min R 1 resonance frequency: ω = There is a valley in p LC admittance at resonance. 1 L Characteristic impedance: ρω=p L = = ω pCC RR R As to a parallel RLC tank circuit: Qpp= = =RCω = 100 ρωp L LC/ Frequency response of the voltage: the magnitude
V 11 I R C = = in L Vout V ω ωω 2 max 1(+−Q 22p )1(+ Q 2 ) p p ω ωωp p
1 ωωω= − YG=22 +−()ω C p ωL V is the maximum V max 1 voltage at resonance Vmax frequency -3 dB 0.7
ω p B =−=ωω21 Qp
101 ω1 ω p ω2 Loaded Q factor
C Is R S L R P R L
load
1 Qp = Unloaded Q ω pLG() ps+ G 1 ′ Rp GGG psL++ 1 QQLp= = = < ωωωppppsLLLLGGG()++
102 Another example
How about the property of “not-quite- parallel RLC tank circuit”?
I L L Please refer to “高频电子线路,张肃文”
I Is V C C
R
103 • Impedance transformation – Matching Network – Series/parallel
104 Series and parallel RC/RL networks
R ρ Q = Q = p ρ s R
What choice of Series RC circuit values makes the two networks Equivalent parallel circuit equivalent?
Here, ω ≈ωs
Series RL circuit Equivalent parallel circuit 105 Series-to-Parallel Conversion (1)
Equating the impedance: 1 Rp 1 jCω p Rs += jCω s 1 Rp + jCω p reforming: 2 RCps jωω=−1 RCRCppss ++( RC pp RC ss) j ω 1 Real part Equation 2 C ω Rp (1) ss = RCp pss RCω =1 = QQsp Rs 1 106 Cppω Series-to-Parallel Conversion (2) Real part equation 2 RCp pss RCω =1 (1)
Image part equation RCpp+− RC ss RC ps =0 (2)
When Cp and Cs are selected, the two impedances remain equal at all frequencies? No!!! An approximation allows equivalence for a narrow frequency range. 1 For a general ω, Substitute RpCp in (1) from (2): = + RRps22 RCssω
Simplified but with constraints, Since Q =1/C ω R , then 2 s s s s RQps=( +1) R s near ωs 2 Qs Substitute Qs into (1): = CCps2 Qs +1 Q2 1 2 s Rp≈ QR ss 107 CCps≈ Parallel-to-Series Conversion
Observations: Typically, Q>4, Series-to-Parallel Conversion: retain the value of the capacitor 2 but raises the resistance by a factor of Qs . Parallel-to-Series Conversion: reduce the resistance by a factor of Q 2. P 108 This statement applies to RL sections as well. Basic Matching Networks a load resistance must be transformed to a lower value.
the capacitor in parallel with RL converts this resistance to a lower series component. The inductance is inserted to cancel the equivalent series capacitance.
≈ ω ωp
RL transformed down by a factor Setting imaginary part to zero (resonate), we have ω≈ ωp
R Q=L = RCω If p 1 Lp1 109 C1ω p Example of Basic Matching Networks
Design the matching network of the following figure so as to transform RL = 50 Ω to 25 Ω at a center frequency of 5 GHz.
Solution:
2 Assuming QP >> 1, we have C1 = 0.90 pF and L1 = 1.13 nH. however, QP = 1.41, 2 indicating the QP >> 1 approximation cannot be used.
We thus obtain C1 = 0.637 pF and L1 = 0.796 nH. 110 Please fill out the detail calculation by yourself! Another Example of Basic Matching Networks
Determine how the circuit shown below transforms RL.
The L1-RL branch to a parallel section produces a higher resistance.
2 2 If QS = (L1ω/RL) >> 1, then the equivalent parallel resistance is
The parallel equivalent inductance is approximately equal to L1 and is cancelled 111 by C1. L-Section topologies L1 transforms RL to a smaller series C transforms R 1 L value while C to a smaller 1 resonates with L series value and 1 L1 cancels C1
L1 transforms RL to a larger C1 transforms RL parallel value to a larger and C1 cancels parallel value the parallel and L1 cancels inductance the parallel capacitance
1. In (a), the power delivered to the input port is 2. Power delivered to the load is 3. if L1 and C1 are ideal, these two powers must be equal:
a network transforming R to a lower value “amplifies” the voltage and attenuates the L 112 current by the above factor. Transfer a Resistance to a Higher Value
if , the parallel combination of C1 and RL can be converted to a series network
Viewing C2 and C1 as one capacitor, Ceq converting the resulting series section to a parallel circuit
RL boosted
Notice: the capacitive component must be cancelled by placing an inductor in parallel with the input. 113 Impedance Matching by Transformers
An ideal transformer having a turns ratio of n “amplifiers” the input voltage by a factor of n.
No power is lost, thus:
114 Observations
The networks studied here operate across a narrow bandwidth (near resonate frequency) transformation ratio, e.g., 1+Q2, varies with frequency;
The capacitance and inductance approximately resonate over a narrow frequency range;
Broadband matching networks can be constructed, but they typically suffer from a high loss.
115 Loss in Matching Networks (1)
Analyze the effect of loss.
We define the loss as the power provided by the input divided by that delivered to RL
The power delivered to Rin1 is entirely absorbed by R P =P . L in1 L The loss of L1 modeled by a series resistance, Rs
This network transforms RL to a lower value, R =R /(1+Q2 ), in1 L P 116 suffering from loss even if Rs appears small. Loss in Matching Networks (2)
The loss of L1 modeled by a parallel resistance, RP.
Pin represents the power delivered by Vin, which is entirely absorbed by RP||RL:
power delivered to the load, PL,
117 Basic matching networks
L-match π-match T-match Tapped capacitor resonator as an impedance matching network Tapped inductor match
118 L-match (refer to P112,116)
There are only two degrees of freedom (one can choose only L and C); Once the impedance transformation ratio and resonant frequency have been specified, network Q is automatically determined;
How to get a different value of Q?
119 π-match
Cascade two L-matches Original circuit L L1 L2
C C C 2 R 1 C R Rin 1 R P in RI 2 P
Parallel RC network Two L-matches connected in cascade, one transforms down one transforms up;
L The load resistance RP is transformed to a L1 2 lower resistance RI at the junction of the two inductances;
C2s R C 1 RI RI is transformed up to a value Rin by a in second L-match section. Series RI equivalent120 π-match: another example C 2
C Rin 1 L R P
Observations:
We have three degrees of freedom (the two capacitance and the sum of two inductances),
We can independently specify center frequency, Q, overall impedance transformation ratio;
In many instance, cascading several matching networks may be helpful. 121 T-match
Connecting up the L-sections L L 1 2 another way leads to the dual of π-match, denoted T-match; R R I in C C 1 2 R S A single capacitor in a practical implementation has RI been decomposed explicitly into two separate ones;
The parallel image resistance
(RI) is seen across these capacitors, either looking to the right or looking to the left.
122 Tapped capacitor match (refer to P107)
(a) capacitive (b) simplified (c) cascading (d) simplified matching circuit circuit with two capacitance circuit with parallel-to-series series-to-parallel conversion conversion
2 1 C p The capacitive divider RRtot = =1 + p ω 2 C “boosts” the value of RP by a RCs( tot ) 1 factor 2 (1+ CCp 1 ) CC1 p Ctot = 123 CC1 + p Tapped inductor match
a) Convert the parallel combination Lp and Rp to series circuit Ls and Rs; b) Combining L1 and Ls into Leq; c) Converting series circuit to parallel circuit and we have: 2 L ≈+1 RRtot 1 p Lp 124 Ltot = LL1 + p Double-tapped resonator
This circuit first boosts R2 to a larger effective parallel resistance across the whole tank than in a L C standard tapped capacitor 1 1 network;
It then reduces this parallel resistance by the tapped Rin L C 2 2 R2 inductors to the desired value Rin.
125