DOCSLIB.ORG

Chapter 7 Unitary Symmetries and QCD As a Gauge Theory

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 7 Unitary Symmetries and QCD As a Gauge Theory Chapter 7 Unitary symmetries and QCD as a gauge theory Literature: Lipkin [23] (group theory concepts from a physicist’s point of view) • Lee [24], chapter 20 (extensive treatment of Lie groups an Lie a!gebras in the • context of ifferentia! geometry) Interactions "etween particles shou! respect some o"served symmetry% &ften, the proce- ure of postu!ating a speci(c symmetry !ea s to a uni)ue theory% *his way of approach is the one of gauge theories% The usual examp!e of a gauge theory is +,-, which correspon s to a !oca!U(1)-symmetry of the La grangian / ieqeχ(x) ψ ψ � 0 e ψ, (1%.) → A A � 0A ∂ χ(x). (1%2) µ → µ µ − µ 2e can co e this comp!icated transformation "ehavior "y rep!acing in the +,- La- grangian∂ µ "y the covariant derivativeD µ 0∂ µ 3 ieqeAµ% 7.1 IsospinSU(2) 4or this section we consi er on!y the strong interaction an ignore the electromagnetic an weak interactions. $n this regar , isobaric nuclei (with the same mass num"er A) are very simi!ar% Heisen"erg propose to interpret protons an neutrons as two states of the same o"ject / the nucleon/ . p 0ψ(x) , | � 0 � � 0 n 0ψ(x) . | � . � � .25 .26 CHAPTER 7. UNITARY SYMMETRIES AND QCD AS A GAUGE THEORY 2e note the analogy to the spin forma!ism of nonrelativistic )uantum mechanics, which originated the name isospin% 1 In isospin'space, p an n can "e represented as a two-component spinor withI0 2 % p has thenI 0| 3� 1 an| �n hasI 0 1 % | � 3 2 | � 3 − 2 :ince the strong interaction is "!in to other charges (e!ectromagnetic charge, weak hy' percharge), the (strong) physics must "e the same for any !inear com"inations of p an n % $n other wor s, for, | � | � p p� 0α p 3β n , | �→| � | � | � n n� 0γ p 3δ n , | �→| � | � | � for some α,β,γ,δ C, or, ∈ ψp N 0 N � 0U N , (1%3) | � ψn → | � | � � � for some 2 2 matrixU with comp!ex entries, t he (strong) physics oes not change if we × switch from N to N � to escri"e the system% | � | � 2e remark at this point that this symmetry is on!y an approximate symmetry since it is violated "y the other interactions, an is hence not a symmetry of nature. First we require the conservation of the norm N N which we interpret as the num"er of particles !ike in )uantum mechanics% This yi�el |s,� ! N N N � N � 0 N U †U N 0 N N � | �→� | � � | | � � | � U †U0UU † 0 U U(2). (7% 4) ⇒ ⇒ ∈ 5 genera! unitary matrix has 4 rea! parameters. :ince the effect ofU an e iϕU are the same, we (x one more parameter "y imposing, etU 0! . U SU(2), (1%8) ⇒ ∈ the special unitary group in 2 imensions. *his group is a Lie group (a group which is at the same time a manifo!d)% 2e use the representation, ˆ U0e iαj Ij , (1%9) where theα j’s are arbitrary group parameters (constant, or epen ing on the spacetime coor inatex), an the I;j’s are the generators of the Lie group% 2e concentrate on in(nitesima! transformations, for whichα j .% $n this approximation we can write � U 3 iα I; . (1%1) ≈ j j 7.1. ISOSPINSU(2) .27 The two e(ning con itions ofSU(2), ,)% (1%4) an (1%8), imp!y then for the generators, ; ; Ij† 0 Ij (hermitian), (1%8) *r I;j 0 0 (traceless). (1%=) In or er for the exponentiation procedure to converge for nonin(nitesimalα j’s, the gen' erators must satisfy a comutation relation, thus e(ning the Lie algebra su(2) of the groupSU(2)% +uite in general, the commutator of two generators must "e expressi"!e as a !inear com' "ination of the other generators 1% In the case of su(2) we have, [I;i, I;j] 0 iεijkI;k, (1%.0) whereε ijk is the total!y antisymmetric tensor withε 123 0 3.% They are characteristic of the (universa! covering group of the) Lie group ("ut in epen ent of the chosen represen' tation) an calle structure constants of the Lie group% The representations can "e characterized accor ing to their tota! isospin% Consi er now I0. 2, where the generators a re given "y . I; 0 ! i 2 i with! i 0" i the @au!i spin matrices (this notation is chosen to prevent confusion with ordinary spin)/ 0 . 0 i . 0 ! 0 ! 0 ! 0 1 . 0 2 i0− 3 0 . � � � � � − � which fu!(!! ["i,"j] 0 2iεijk"k. *he action of the matrices of the representation (see ,)% (1%6)) is a non'a"elian phase transformation/ #» #» iα τ N � 0e · 2 N . | � | � 4orSU(2), there exists on!y one ia gona! matrix (!3). In genera!, forSU(N), the fo!!owing ho! s true: Rankr0N ./ *here arer simu!taneous!y iagona ! operators. • − Dimension of the Lie a!gebra#0N 2 ./ *here are# generators of the group an • − therefore# group parameters. ,% g. in the case ofSU(2) ∼0 S$(3) this means that there are three rotations/generators an three ang!es{± as} parameters. 1Since we are working in a matrix representation ofSU(2) this statement mak es sense. The difference between the abstract group and its matrix representation is often neglected. .28 CHAPTER 7. UNITARY SYMMETRIES AND QCD AS A GAUGE THEORY � ���� �������� �3 �� �� Figure 1%./ The nucleons n and p form an isospin double t. | � | � Isospin particle mu!tip!ets (representations) can "e characterized "y their )uantum num' "ersI an I 3/ There are 2I 3 . states. Consi er for examp!e once again the caseI0. 2. There are two states, characterize "y theirI 3 )uantum num"er/ I0 1 ,I 0 3 1 p 2 3 2 0 | � . I0 1 ,I 0 1 n �� 2 3 − 2 �� �| �� � � � This is visua!ized in Fig% 1%1, a!ong� with the action of the operators! 0 . 2(!1 iτ2): ± ± 0 0 . 0 ! p 0 0 0 n − | � . 0 0 . | � � � � � � � ! n 0 p + | � | � ! n 0! + p 00. − | � | � This is the sma!!est non-trivia! representation of SU(2) an therefore its fun amenta! representation% 4urther examp!es for isospin mu!tip!ets are I mu!tip!ets I3 + 3 1 1 p % 2He 3 2 2 n %0 36 1 � � � � �1 � − 2 &+ 3. &0 0 &− . ++ −3 B 3 2 + 1 3 B 3 2 2 0 1 B 2 − 3 B− − 2 wherem 1232 MeD an m 93< MeV. Δ ≈ p,n ≈ 5!!I� . representations can " e o"taine from irect pro ucts out of the fun amental I0. 2 representation 2 where “2F enotes the num"er of states. In ana!ogy to the a ition of two electron spins where the ?!ebsch'Gor an ecomposition rea s rep% 1/2 ⊗ 7.1. ISOSPINSU(2) .29 rep%1/2 0 rep%0 rep%1 an where there are two states for the spin'.A2 representation, one state for the spin-0⊕ representation, an three states for the spin'. representation, we have 2 2 0 . 3 . (7%.1) ⊗ ⊕ I= 1 1 =0,1 isosinglet,I=0 isotriplet,I=1 | 2 ± 2 | However, there is an important� �� �ifference "etwee���� n isospin���� an spin mu!tip!ets. $n the !atter case, we are consi ering a "oun system an the constituents carrying the spin have the same mass. &n the other han , pions are not simp!e "oun states. Their structure wi!! "e escri"ed "y the )uark mo el% 7.1.1 Isospin invariant interactions Isospin invariant interactions can "e constructed "y choosingSU(2) invariant interaction terms �. 4or instance, consi er the Hukawa mo e!, escri"ing nucleon'pion coup!ing, whereL #» #» #» #» � 0 igNI !N &0 ig NI � !N � & � (1%.2) LπN · · which is an isovector an where the secon i entity is ue toSU(2) invariance% In(nites ' ima!!y, the transformation !ooks as fo!!ows: i #» #» N � 0UN U03 α ! (1%.3) 2 · i #» #» 1 NI � 0 NUI † U † 0 α !0U − (1%.4) − 2 · #» #» #» #» & � 0( &(03i α t . (1%.5) · #» The parameters t can "e etermine from the isospin invariance con ition in ,)% (1%12): 1 N!I jN&j 0 NUI − !iUN(ij&j. With( ij 0δ ij 3 iαk(tk)ij (cp% ,)% (1%.8)) an inserting the expressions forU an U †, this yiel s i i ! 0 α ! ! 3 α ! δ 3 iα (t ) j − 2 k k i 2 k k ij k k ij � � � � � � i 2 =τ i + 2 αk[τi, τk] + (α k) i O 2 =τ i + αk2iεiklτl + (α ) � 2 �� O k � 0! 3 iα iε ! 3! (t ) j k { jkl l i k ij} 0! 3 iα ! iε 3 (t ) j k i { jki k ij} ! =0 (t ) 0 iε . ⇒ k ij −� kij �� � .30 CHAPTER 7. UNITARY SYMMETRIES AND QCD AS A GAUGE THEORY This means that the 3 3 matricest k,)0.,2,3, are given "y the struct ure constants (see ,)% (7..0))% 4or the×commutator we therefore have [t , t ] 0 ε ε 3ε ε 0ε ε 0 iε ( iε ) 0 iε (t ) (1%.9) k l ij − kim lmj lim kmj klm mij klm − mij klm m ij where the secon i entity fo!!ows using the Jaco"i i entity% This means that the matrices tk fu!(!! the Lie algebra [tk, tl] 0 iεklmtm. Thet ks form the a joint representation ofSU(2). 7.2 Quark model of hadrons It is experimental!y we!! esta"!ishe that the proton and the neutron have inner structure.
Load more

Recommended publications
  • QCD Theory 6Em2pt Formation of Quark-Gluon Plasma In
    QCD theory Formation of quark-gluon plasma in QCD T. Lappi University of Jyvaskyl¨ a,¨ Finland Particle physics day, Helsinki, October 2017 1/16 Outline I Heavy ion collision: big picture I Initial state: small-x gluons I Production of particles in weak coupling: gluon saturation I 2 ways of understanding glue I Counting particles I Measuring gluon field I For practical phenomenology: add geometry 2/16 A heavy ion event at the LHC How does one understand what happened here? 3/16 Concentrate here on the earliest stage Heavy ion collision in spacetime The purpose in heavy ion collisions: to create QCD matter, i.e. system that is large and lives long compared to the microscopic scale 1 1 t L T > 200MeV T T t freezefreezeout out hadronshadron in eq. gas gluonsquark-gluon & quarks in eq. plasma gluonsnonequilibrium & quarks out of eq. quarks, gluons colorstrong fields fields z (beam axis) 4/16 Heavy ion collision in spacetime The purpose in heavy ion collisions: to create QCD matter, i.e. system that is large and lives long compared to the microscopic scale 1 1 t L T > 200MeV T T t freezefreezeout out hadronshadron in eq. gas gluonsquark-gluon & quarks in eq. plasma gluonsnonequilibrium & quarks out of eq. quarks, gluons colorstrong fields fields z (beam axis) Concentrate here on the earliest stage 4/16 Color charge I Charge has cloud of gluons I But now: gluons are source of new gluons: cascade dN !−1−O(αs) d! ∼ Cascade of gluons Electric charge I At rest: Coulomb electric field I Moving at high velocity: Coulomb field is cloud of photons
    [Show full text]
  • The Positons of the Three Quarks Composing the Proton Are Illustrated
    The posi1ons of the three quarks composing the proton are illustrated by the colored spheres. The surface plot illustrates the reduc1on of the vacuum ac1on density in a plane passing through the centers of the quarks. The vector field illustrates the gradient of this reduc1on. The posi1ons in space where the vacuum ac1on is maximally expelled from the interior of the proton are also illustrated by the tube-like structures, exposing the presence of flux tubes. a key point of interest is the distance at which the flux-tube formaon occurs. The animaon indicates that the transi1on to flux-tube formaon occurs when the distance of the quarks from the center of the triangle is greater than 0.5 fm. again, the diameter of the flux tubes remains approximately constant as the quarks move to large separaons. • Three quarks indicated by red, green and blue spheres (lower leb) are localized by the gluon field. • a quark-an1quark pair created from the gluon field is illustrated by the green-an1green (magenta) quark pair on the right. These quark pairs give rise to a meson cloud around the proton. hEp://www.physics.adelaide.edu.au/theory/staff/leinweber/VisualQCD/Nobel/index.html Nucl. Phys. A750, 84 (2005) 1000000 QCD mass 100000 Higgs mass 10000 1000 100 Mass (MeV) 10 1 u d s c b t GeV HOW does the rest of the proton mass arise? HOW does the rest of the proton spin (magnetic moment,…), arise? Mass from nothing Dyson-Schwinger and Lattice QCD It is known that the dynamical chiral symmetry breaking; namely, the generation of mass from nothing, does take place in QCD.
    [Show full text]
  • Modern Methods of Quantum Chromodynamics
    Modern Methods of Quantum Chromodynamics Christian Schwinn Albert-Ludwigs-Universit¨atFreiburg, Physikalisches Institut D-79104 Freiburg, Germany Winter-Semester 2014/15 Draft: March 30, 2015 http://www.tep.physik.uni-freiburg.de/lectures/QCD-WS-14 2 Contents 1 Introduction 9 Hadrons and quarks . .9 QFT and QED . .9 QCD: theory of quarks and gluons . .9 QCD and LHC physics . 10 Multi-parton scattering amplitudes . 10 NLO calculations . 11 Remarks on the lecture . 11 I Parton Model and QCD 13 2 Quarks and colour 15 2.1 Hadrons and quarks . 15 Hadrons and the strong interactions . 15 Quark Model . 15 2.2 Parton Model . 16 Deep inelastic scattering . 16 Parton distribution functions . 18 2.3 Colour degree of freedom . 19 Postulate of colour quantum number . 19 Colour-SU(3).............................. 20 Confinement . 20 Evidence of colour: e+e− ! hadrons . 21 2.4 Towards QCD . 22 3 Basics of QFT and QED 25 3.1 Quantum numbers of relativistic particles . 25 3.1.1 Poincar´egroup . 26 3.1.2 Relativistic one-particle states . 27 3.2 Quantum fields . 32 3.2.1 Scalar fields . 32 3.2.2 Spinor fields . 32 3 4 CONTENTS Dirac spinors . 33 Massless spin one-half particles . 34 Spinor products . 35 Quantization . 35 3.2.3 Massless vector bosons . 35 Polarization vectors and gauge invariance . 36 3.3 QED . 37 3.4 Feynman rules . 39 3.4.1 S-matrix and Cross section . 39 S-matrix . 39 Poincar´einvariance of the S-matrix . 40 T -matrix and scattering amplitude . 41 Unitarity of the S-matrix . 41 Cross section .
    [Show full text]
  • The Center Symmetry and Its Spontaneous Breakdown at High Temperatures
    CORE Metadata, citation and similar papers at core.ac.uk Provided by CERN Document Server THE CENTER SYMMETRY AND ITS SPONTANEOUS BREAKDOWN AT HIGH TEMPERATURES KIERAN HOLLAND Institute for Theoretical Physics, University of Bern, CH-3012 Bern, Switzerland UWE-JENS WIESE Center for Theoretical Physics, Laboratory for Nuclear Science and Department of Physics, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA The Euclidean action of non-Abelian gauge theories with adjoint dynamical charges (gluons or gluinos) at non-zero temperature T is invariant against topologically non-trivial gauge transformations in the ZZ(N)c center of the SU(N) gauge group. The Polyakov loop measures the free energy of fundamental static charges (in- finitely heavy test quarks) and is an order parameter for the spontaneous break- down of the center symmetry. In SU(N) Yang-Mills theory the ZZ(N)c symmetry is unbroken in the low-temperature confined phase and spontaneously broken in the high-temperature deconfined phase. In 4-dimensional SU(2) Yang-Mills the- ory the deconfinement phase transition is of second order and is in the universality class of the 3-dimensional Ising model. In the SU(3) theory, on the other hand, the transition is first order and its bulk physics is not universal. When a chemical potential µ is used to generate a non-zero baryon density of test quarks, the first order deconfinement transition line extends into the (µ, T )-plane. It terminates at a critical endpoint which also is in the universality class of the 3-dimensional Ising model. At a first order phase transition the confined and deconfined phases coexist and are separated by confined-deconfined interfaces.
    [Show full text]
  • The Confinement Problem in Lattice Gauge Theory
    The Confinement Problem in Lattice Gauge Theory J. Greensite 1,2 1Physics and Astronomy Department San Francisco State University San Francisco, CA 94132 USA 2Theory Group, Lawrence Berkeley National Laboratory Berkeley, CA 94720 USA February 1, 2008 Abstract I review investigations of the quark confinement mechanism that have been carried out in the framework of SU(N) lattice gauge theory. The special role of ZN center symmetry is emphasized. 1 Introduction When the quark model of hadrons was first introduced by Gell-Mann and Zweig in 1964, an obvious question was “where are the quarks?”. At the time, one could respond that the arXiv:hep-lat/0301023v2 5 Mar 2003 quark model was simply a useful scheme for classifying hadrons, and the notion of quarks as actual particles need not be taken seriously. But the absence of isolated quark states became a much more urgent issue with the successes of the quark-parton model, and the introduction, in 1972, of quantum chromodynamics as a fundamental theory of hadronic physics [1]. It was then necessary to suppose that, somehow or other, the dynamics of the gluon sector of QCD contrives to eliminate free quark states from the spectrum. Today almost no one seriously doubts that quantum chromodynamics confines quarks. Following many theoretical suggestions in the late 1970’s about how quark confinement might come about, it was finally the computer simulations of QCD, initiated by Creutz [2] in 1980, that persuaded most skeptics. Quark confinement is now an old and familiar idea, routinely incorporated into the standard model and all its proposed extensions, and the focus of particle phenomenology shifted long ago to other issues.
    [Show full text]
  • Phenomenological Review on Quark–Gluon Plasma: Concepts Vs
    Review Phenomenological Review on Quark–Gluon Plasma: Concepts vs. Observations Roman Pasechnik 1,* and Michal Šumbera 2 1 Department of Astronomy and Theoretical Physics, Lund University, SE-223 62 Lund, Sweden 2 Nuclear Physics Institute ASCR 250 68 Rez/Prague,ˇ Czech Republic; [email protected] * Correspondence: [email protected] Abstract: In this review, we present an up-to-date phenomenological summary of research developments in the physics of the Quark–Gluon Plasma (QGP). A short historical perspective and theoretical motivation for this rapidly developing field of contemporary particle physics is provided. In addition, we introduce and discuss the role of the quantum chromodynamics (QCD) ground state, non-perturbative and lattice QCD results on the QGP properties, as well as the transport models used to make a connection between theory and experiment. The experimental part presents the selected results on bulk observables, hard and penetrating probes obtained in the ultra-relativistic heavy-ion experiments carried out at the Brookhaven National Laboratory Relativistic Heavy Ion Collider (BNL RHIC) and CERN Super Proton Synchrotron (SPS) and Large Hadron Collider (LHC) accelerators. We also give a brief overview of new developments related to the ongoing searches of the QCD critical point and to the collectivity in small (p + p and p + A) systems. Keywords: extreme states of matter; heavy ion collisions; QCD critical point; quark–gluon plasma; saturation phenomena; QCD vacuum PACS: 25.75.-q, 12.38.Mh, 25.75.Nq, 21.65.Qr 1. Introduction Quark–gluon plasma (QGP) is a new state of nuclear matter existing at extremely high temperatures and densities when composite states called hadrons (protons, neutrons, pions, etc.) lose their identity and dissolve into a soup of their constituents—quarks and gluons.
    [Show full text]
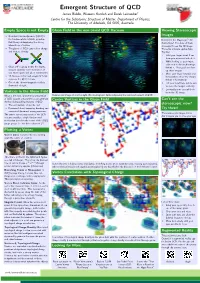
  • Emergent Structure Of
    Emergent Structure of QCD James Biddle, Waseem Kamleh and Derek Leinwebery Centre for the Subatomic Structure of Matter, Department of Physics, The University of Adelaide, SA 5005, Australia Empty Space is not Empty Gluon Field in the non-trivial QCD Vacuum Viewing Stereoscopic Images Quantum Chromodynamics (QCD) is the fundamental relativistic quantum Remember the Magic Eye R 3D field theory underpinning the strong illustrations? You stare at them interactions of nature. cross-eyed to see the 3D image. The gluons of QCD carry colour charge The same principle applies here. and interact directly Try this! 1. Hold your finger about 5 cm from your nose and look at it. 2. While looking at your finger, take note of the double image Gluon self-coupling makes the empty behind it. Your goal is to line vacuum unstable to the formation of up those images. non-trivial quark and gluon condensates. 3. Move your finger forwards and 16 chromo-electric and -magnetic fields backwards to move the images compose the QCD vacuum. behind it horizontally. One of the chromo-magnetic fields is 4. Tilt your head from side to side illustrated at right. to move the images vertically. 5. Eventually your eyes will lock Vortices in the Gluon Field in on the 3D image. What is the most fundamental perspective Stereoscopic image of one the eight chromo-magnetic fields composing the nontrivial vacuum of QCD. of QCD vacuum structure that can generate Centre Vortices in the Gluon Field Can't see the the key distinguishing features of QCD stereoscopic view? The confinement of quarks, and Dynamical chiral symmetry breaking and Try these! associated dynamical-mass generation.
    [Show full text]
  • Quantum Chromodynamics (QCD) QCD Is the Theory That Describes the Action of the Strong Force
    Quantum chromodynamics (QCD) QCD is the theory that describes the action of the strong force. QCD was constructed in analogy to quantum electrodynamics (QED), the quantum field theory of the electromagnetic force. In QED the electromagnetic interactions of charged particles are described through the emission and subsequent absorption of massless photons (force carriers of QED); such interactions are not possible between uncharged, electrically neutral particles. By analogy with QED, quantum chromodynamics predicts the existence of gluons, which transmit the strong force between particles of matter that carry color, a strong charge. The color charge was introduced in 1964 by Greenberg to resolve spin-statistics contradictions in hadron spectroscopy. In 1965 Nambu and Han introduced the octet of gluons. In 1972, Gell-Mann and Fritzsch, coined the term quantum chromodynamics as the gauge theory of the strong interaction. In particular, they employed the general field theory developed in the 1950s by Yang and Mills, in which the carrier particles of a force can themselves radiate further carrier particles. (This is different from QED, where the photons that carry the electromagnetic force do not radiate further photons.) First, QED Lagrangian… µ ! # 1 µν LQED = ψeiγ "∂µ +ieAµ $ψe − meψeψe − Fµν F 4 µν µ ν ν µ Einstein notation: • F =∂ A −∂ A EM field tensor when an index variable µ • A four potential of the photon field appears twice in a single term, it implies summation µ •γ Dirac 4x4 matrices of that term over all the values of the index
    [Show full text]
  • QFT II Solution 7
    QFT II FS 2019 Solution 7. Prof. M. Grazzini Exercise 1. Remaining Feynman rules for QCD Starting from the full QCD-Lagrangian with gauge-fixing and Fadeev-Popov term, 1 1 2 L = − F a F a,µν + ¯iD= − m − @µAa − c¯a@µDabcb ; (1) QCD 4 µν 2ξ µ µ find the terms of Lint contributing to the gluon-quark and the gluon-ghost vertices and derive the corre- sponding Feynman rules using path-integral methods. Solution. The first term, the pure Yang-Mills Lagrangian, only contributes to the gluon self- interaction we calculated on sheet 6. The gauge fixing term is quadratic in the fields and will therefore not contribute to any interaction. We are left with the second and fourth term, and the corresponding contributions to Lint will become obvious once we write out the covariant derivatives. For the quarks (fundamental representation) we have a a Dµ i = (@µδij − igtijAµ) j ; (S.1) and for the ghosts (adjoint representation) ab b ab abc c b Dµ c = (@µδ − gf Aµ)c : (S.2) With this we find gqq¯ ¯ a a gcc¯ abc µ a c b Lint = g itijA= j ; Lint = −gf (@ c¯ )Aµc ; (S.3) where we shifted the derivative to act on the anti-ghost by means of partial integration. To derive the vertices we expand the exponential in a a a Z[Jµ; a¯i; ai; η¯ ; η ] Z 4 1 δ 1 δ 1 δ 1 δ 1 δ a a a = N exp i d zLint a ; ; − ; a ; − a Z0[Jµ; a¯i; ai; η¯ ; η ] (S.4) i δJµ i δa¯i i δai i δη¯ i δη a a a to first order, as usual.a ¯i; ai are the sources for the quarks,η ¯ ; η for the ghosts and Jµ for the gluon-field.
    [Show full text]
  • Instantons at Work
    Instantons at work Dmitri Diakonov1,2 1NORDITA, Denmark 2St. Petersburg Nuclear Physics Institute, Russia Abstract The aim of this review is to demonstrate that there exists a coherent picture of strong interactions, based on instantons. Starting from the first principles of Quantum Chromo- dynamics – via the microscopic mechanism of spontaneous chiral symmetry breaking – one arrives to a quantitative description of the properties of light hadrons, with no fitting parameters. The discussion of the importance of instanton-induced interactions in soft high-energy scattering is new. Contents 1 Introduction 2 2 What are instantons? 5 2.1 Periodicity of the Yang–Mills potential energy ................... 5 2.2 Instantons in simple words .............................. 7 2.3 Instanton configurations ............................... 9 2.4 Instanton collective coordinates ........................... 10 2.5 Gluon condensate ................................... 11 2.6 One-instanton weight ................................. 13 2.7 Instanton ensemble .................................. 15 arXiv:hep-ph/0212026v4 16 Apr 2003 3 Non-instanton semiclassical configurations 18 4 Chiral symmetry breaking by instantons 26 4.1 Chiral symmetry breaking by definition ....................... 26 4.2 Physics: quarks hopping from one instanton to another .............. 29 4.3 Quark propagator and dynamical quark mass .................... 31 5 Instanton-induced interactions 35 6 Effective Chiral Lagrangian 40 7 Chromomagnetic pomeron 41 8 Baryons 47 9 Chiral Quark–Soliton Model 49 10 Summary 51 1 1 Introduction Strong interactions as described by Quantum Chromodynamics (QCD) is a remarkable branch of physics where the observable entities – hadrons and nuclei – are very far from quarks and gluons in terms of which the theory is formulated. To make matters worse, the scale of strong interactions 1 fm is nowhere to be found in the QCD Lagrangian.
    [Show full text]
  • QCD and Renormalisation Group Methods
    QCD and Renormalisation Group Methods Lecture presented at Herbstschule f¨ur Hochenergiephysik Maria Laach, 2006 by Matthias Jamin ICREA & IFAE Universitat Aut`onoma de Barcelona E-08193 Bellaterra, Barcelona, Spain [email protected] Version of 1.9.2006 Contents 1 Introduction 1 1.1 QCDbasics ................................... 2 1.2 Dimensionalregularisation . .... 6 1.3 Renormalisationatone-loop . ... 12 2 Renormalisation Group 18 2.1 Renormalisationgroupequation . .... 18 2.2 Runninggaugecoupling . .. .. 19 2.3 Runningquarkmass .............................. 22 3 Applications 23 3.1 e+e−-scatteringtohadrons . .. .. 23 3.2 QCDsumrules ................................. 27 3.3 Contourimprovedperturbationtheory . ..... 32 3.4 Renormalisation of composite operators . ....... 33 3.5 TheweakeffectiveHamiltonian . .. 35 A Solutions to the exercises 44 i Chapter 1 Introduction In the following lecture, renormalisation group methods in the context of quantum field theory will be discussed. Most concepts and applications will be investigated on the basis of QCD, the theory of the strong interactions. The following material is mainly taken from the following textbooks and review articles [1–9]. Further references will be mentioned when they are required for a specific topic. Along the lecture, many problems will be presented which should be worked out explicitly in order to deepen the understanding of the subject, or practice computational skills. Often, the problems ask to perform a computation in a special case, in order to get the main idea, but then in the solution, more general cases are discussed, since the additional structure might shed further light on the interpretation of the results. Historically, the method of the renormalisation group was first introduced by St¨uckelberg and Petermann [10] as well as Gell-Mann and Low [11], as a means to deal with the failure of perturbation theory in quantum electrodynamics at very high energies.
    [Show full text]
  • M.Guenin University of Genera, Switzerland 1. Green's Functions Of
    RELATIVISTIC QUANTUM FIELD TK30RY WITHOUT is still far from complete, specially from ASYMPTOTIC PARTICLES AND QUARKS CONFINEMENT a conceptual point of view, in particular the M.Guenin causal behaviour is rather tricky. University of Genera, Switzerland We can define a field theory by simply giving its vertex and its propagators, this is at least true for the perturbative expansion 1. Green’s Functions of Quantum Field Theories of the ^-matrix and for writing the Bethe-Sal- The бгееп’e functions of a field theory are peter equation. In such a case, it is of course determined Ъу imposing a certain number of bo­ necessary to verify that it corresponds to undary conditions. Among them, is a condition a relativistic, local, causal theory if one on the behaviour at infinity which is usually wants such properties to be true. tacitely assumed, namely that the Green func­ We define what we call a space-like field tion should vanish at infinity in X space. theory for a scalar or vector gluon by the rules: The reason for the existence of this condition 1) Write the propagator inX space, as Bes­ is that one wants asymptotically free particles, sel function (this is necessary because our because a non vanishing propagator function, at propagator does not have a Fourier transform infinity implies a non vanishing potential for in the usual sense). the particles at infinity. 2) T^e space-like theory is obtained from This postulate is therefore perfectly the Feynman form by replacing № by - tyl. justified for standard scattering systems in This gluon field can be coupled with which the particles can be considered as asymp­ a Fermion quark field.
    [Show full text]