DOCSLIB.ORG

Pimmaj Thesis.Pdf

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Pimmaj Thesis.Pdf The University of Nottingham Department of Mechanical, Materials and Manufacturing Engineering Analysis of Flexible Fabric Structures Thesis submitted to the University of Nottingham for the degree of Doctor of Philosophy by Andrew James Pimm July 2011 Abstract This thesis is primarily aimed at carrying out analysis of Energy Bags, reinforced fabric bags used for subsea compressed air energy storage. Subsea compressed air energy storage is a completely new method of large-scale energy storage designed to be integrated with direct- compression offshore wind turbines and wave energy converters. Energy Bags are impermeable bags anchored to the seabed at significant depths (e.g. 500m) in which high pressure air, compressed by specially designed wind turbines and wave energy converters, is stored at pressures roughly equal to the hydrostatic pressure of the surrounding water. Energy Bags do not need to be particularly strong because most of the reaction to the pressure load is provided by the surrounding water, and high energy densities are available at such depths as 500m. This thesis investigates the deformed shapes of Energy Bags and studies optimal designs. Three analysis methods are developed which vary in their complexity, ease of use, and accuracy. First, a system of coupled ordinary differential equations (ODEs) is derived which describes the deformed shape of an axisymmetric Energy Bag. This model is later used in an optimisation study to find the shapes of bag which minimise the cost of materials (reinforcement, fabric, and ballast) per unit of energy stored. Circumferential reinforcement, hanging masses from the inside of the bag (which it was hoped would lower the total cost) and fill level are all included as variables in the optimisation, and it is found that for reasonable materials costs an Energy Bag could cost less than £10,000/MWh when anchored at 500m. This compares favourably with all other methods of large-scale energy storage. However, the bags used in the optimisation study have wide bases, which will require sealing against the seabed (unless water is to be allowed into the bags). Problems are encountered when trying to use the ODE method to find the shapes of partially inflated bags, and it is generally not very easy to use. Next, we carry out finite element analysis (FEA) of an axisymmetric Energy Bag using cable elements. This is much more user-friendly and flexible than the ODE method. Partially inflated bag shapes are found, and pressure-volume curves are presented which show the almost isobaric performance of an Energy Bag. It is found that material mass limits the extent to which the bag can be deflated before it becomes unstable. The axisymmetric FEA is used to study bags with much more realistic circumferential reinforcement than the ODE method, and we also look at bags with an unsealed base, which allow water in through the base as they deflate. ii A three-dimensional FEA tool is presented which models an Energy Bag as a cable- reinforced membrane using cable and membrane elements, and special measures had to be taken to deal with wrinkling. We assume that the bag is rotationally symmetric, comprising a number of symmetric lobes. The 3D FEA is used to find the stress distribution in the membrane of the bag, however a converged solution cannot always be found. It is not certain why this is the case but it is anticipated that it is because deformed bags are not always rotationally symmetric. The 3D FEA could also be used to model other membrane structures such as balloons, parachutes, roofs and sails, as well as nets. The standard cutting patterns for lobes in lobed balloons are analysed, and a new cutting pattern known as the Constant Tension lobe is generated. This is an extension of the Constant Radius lobe and takes into account the pressure gradient found in both air and water, minimising waste material. The Constant Tension lobe is particularly appropriate for Energy Bags because of the large pressure gradient in water. The Ultra High Performance Vessel architecture is also presented, upon which the design of the prototype Energy Bags is based. The fabric structure of an Ultra High Performance Vessel comprises only two sheets of fabric (rather than many separate lobes welded together), and tendon shortening and “bellows” serve to ensure that there is no meridional stress in the fabric. An analytical optimisation is used to show that the zero pressure bag that minimises cost of materials per unit of energy stored has equal costs of reinforcement and membrane. The axisymmetric FEA is also used to find the optimum bag size and maximum fill level for a bag which comes down to a single point at the base (as opposed to a wide base bag). Finally, testing of two 1.8m diameter superpressure Energy Bags has been commenced during the course of this work, and the prototypes and test rig are documented in this thesis. The prototypes were manufactured for us by Thin Red Line Aerospace Ltd., a Canadian manufacturer of deployable fabric structures for use in space. They are being cycled back-to-back in order to prove the concept, assess the performance of an Energy Bag over time, and identify any problems that need to be addressed. One of the bags had a few small leaks from the moment it was first inflated, but the other has remained airtight to date. It was found that if an Energy Bag is to be airtight, special attention must be paid to the welds at the seams and the sealing around the airline fittings. iii Acknowledgements First and foremost I would like to thank my supervisor, Professor Seamus Garvey, for guiding me through the project with such vigour and expertise, and Dr Richard Drew of E.ON New Build and Technology for providing valuable support and ensuring that the project has progressed on schedule. I would also like to thank my internal assessor, Professor Adib Becker, for giving useful feedback at my progression assessments, and Maxim De Jong of Thin Red Line Aerospace for showing such enthusiasm for the idea, manufacturing the prototypes, and guiding me to some very useful literature. Dr Cosimo Buffone and the technicians in the university laboratories provided help with setting up the testing that is very much appreciated, and my associate supervisor, Dr Mike Wood, has also been supportive. I would also like to thank Gran for giving me so much help with maths and physics at school and for getting me interested in renewable energy, and Jenny, Mum and Dad, and all my family and friends for their love and support. iv Contents 1 Introduction ....................................................................................................................... 1 1.1 Fossil Fuels and their Drawbacks ..................................................................... 1 1.2 Energy Storage and ICARES ............................................................................ 5 1.3 Fabric Structures ............................................................................................. 16 1.4 Aims and Scope .............................................................................................. 17 1.5 Layout of the Thesis ........................................................................................ 18 2 Literature Review ........................................................................................................... 20 2.1 Energy Storage ................................................................................................ 20 2.1.1 Compressed Air ........................................................................................... 21 2.1.2 Pumped Hydro ............................................................................................ 30 2.1.3 Batteries ...................................................................................................... 32 2.1.4 Flow Batteries ............................................................................................. 33 2.1.5 Flywheels .................................................................................................... 34 2.1.6 Superconductors (SMES) ............................................................................ 35 2.1.7 Hydrogen ..................................................................................................... 36 2.1.8 Thermal Energy Storage ............................................................................. 37 2.2 Underwater Inflatables and Water Load Test Weights ................................... 39 2.2.1 Lifting Bags ................................................................................................. 40 2.2.2 Water Load Test Weights ............................................................................ 46 2.2.3 Correspondence with Manufacturers .......................................................... 49 2.3 Ballooning ....................................................................................................... 50 2.3.1 Early Days of Ballooning ............................................................................ 50 2.3.2 Scientific Ballooning and Superpressure Balloons ..................................... 52 2.3.3 Wrinkling of Membranes ............................................................................. 61 2.3.4 The Young-Laplace Equation ...................................................................... 63 2.4 Techniques in Nonlinear Finite Element Analysis .......................................... 64 2.4.1 The Newton-Raphson Method ....................................................................
Load more

Recommended publications
  • Dive Theory Guide
    DIVE THEORY STUDY GUIDE by Rod Abbotson CD69259 © 2010 Dive Aqaba Guidelines for studying: Study each area in order as the theory from one subject is used to build upon the theory in the next subject. When you have completed a subject, take tests and exams in that subject to make sure you understand everything before moving on. If you try to jump around or don’t completely understand something; this can lead to gaps in your knowledge. You need to apply the knowledge in earlier sections to understand the concepts in later sections... If you study this way you will retain all of the information and you will have no problems with any PADI dive theory exams you may take in the future. Before completing the section on decompression theory and the RDP make sure you are thoroughly familiar with the RDP, both Wheel and table versions. Use the appropriate instructions for use guides which come with the product. Contents Section One PHYSICS ………………………………………………page 2 Section Two PHYSIOLOGY………………………………………….page 11 Section Three DECOMPRESSION THEORY & THE RDP….……..page 21 Section Four EQUIPMENT……………………………………………page 27 Section Five SKILLS & ENVIRONMENT…………………………...page 36 PHYSICS SECTION ONE Light: The speed of light changes as it passes through different things such as air, glass and water. This affects the way we see things underwater with a diving mask. As the light passes through the glass of the mask and the air space, the difference in speed causes the light rays to bend; this is called refraction. To the diver wearing a normal diving mask objects appear to be larger and closer than they actually are.
    [Show full text]
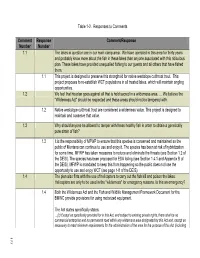
  • Final EIS Responses to Comments 1-40
    Table 1-2. Responses to Comments Comment Response Comment/Response Number Number 1.1 The lakes in question are in our main camp area. We have operated in this area for thirty years and probably know more about the fish in these lakes than anyone associated with this ridiculous plan. These lakes have provided unequalled fishing to our guests and all others that have fished them. 1.1 This project is designed to preserve this stronghold for native westslope cutthroat trout. This project proposes to re-establish WCT populations in all treated lakes, which will maintain angling opportunities. 1.2 We feel that his plan goes against all that is held sacred in a wilderness area. … We believe the "Wilderness Act" should be respected and these areas should not be tampered with. 1.2 Native westslope cutthroat trout are considered a wilderness value. This project is designed to maintain and conserve that value. 1.3 Why should anyone be allowed to tamper with these healthy fish in order to obtain a genetically pure strain of fish? 1.3 It is the responsibility of MFWP to ensure that this species is conserved and maintained so the public of Montana can continue to use and enjoy it. The species has been at risk of hybridization for some time. MFWP has taken measures to reduce and eliminate the threats (see Section 1.2 of the DEIS). The species has been proposed for ESA listing (see Section 1.4.1 and Appendix B of the DEIS). MFWP is mandated to keep this from happening so the public does not lose the opportunity to use and enjoy WCT (see page 1-8 of the DEIS).
    [Show full text]
  • Quality Rental Tools and Equipment– Well Serviced, Priced Right
    RENTAL CATALOG QUALITY RENTAL TOOLS AND EQUIPMENT– WELL SERVICED, PRICED RIGHT. RENTAL INDEX CORE DRILLS SAFETY AIR COMPRESSORS Core Drills . 1 Confined Space Tripod . 13 Air Compressors - Tow Behind . 24 Accessories . 1 Davit System . 13 Air Compressors - Electric . 24 Bits . 2 Fall Protection Carts . 13 Retractable Lifelines . 13 BREAKERS ELECTRICAL Horizontal Lifelines . 13 Air (30lb, 60lb and 90lb) . 25 Cable Cutters . 3 Gas Monitors . 13 Electric . 25 Cable Crimpers . 3 Monitor Pumps . 13 Air Hose . 25 Cable Pullers . 3 Cable Sheaves . 3 BLOWERS BAKER SCAFFOLD Pull Monitor . 3 Blowers . 14 Baker Scaffold . 25 Cable Feeder . 5 Reel Stands . 5 MATERIAL LIFTS AIR TOOLS Reel Stand Spindles . 5 Material Lifts . 14 Rivet Buster . 26 Rod and Strut Cutters . 5 Roustabouts . 14 Rivet Buster Bits . .26 Conduit Benders . 5-6 A/C Lift and Mover . 14 Scalers . 26 Conduit Cart . 6 Gantry . .15 Chippers . 26 Knock Out Sets . 6 Bits for Air Chippers . 26 Cable Stripper . 6 HYDRAULIC CYLINDERS Impacts . 26 Hydraulic Cylinders/Bags . 15-16 Air Hose . 26 RADIOS Hydraulic Pumps and Hoses . 16 Saws . 28 Radios . 6 TORQUE TOOLS COMPACTION PIPING TOOLS Hand Torque Wrenches . 16 Plate Compactor . .28 Threaders . 7 Cordless Torque Wrenches . 18 Jumping Jack Tampers . 28 Threader Accessories . 7 Hydraulic Torque Wrenches . 18 Roll Groovers . 7 Punches . 18 GENERATORS AND PUMPS Groover Accessories . 9 Generators . 28 See Snake Camera . 9 CHAIN HOISTS Gas Pumps . 29 Locators . 9 Hand Chainfall Hoist . 18-19 Electric Pumps . 29 Pipe Freeze Kits . 9 Hand Lever Hoist (Come-A-Long) . 19 Pipe Thawers . 9 Electric Chainfalls . 20-21 WELDING T-Drills . 9 Air Hoist .
    [Show full text]
  • Diving Incidents Report Foreward Introduction
    APPENDIX A - DIVING INCIDENTS REPORT FOREWARD The 1992 Diving Incidents Report, produced by The British Sub-Aqua Club (BSAC) in the interest of promoting diving safety. As the Goveming Body of the sport of sub-aqua diving within the United Kingdom, the BSAC publishes this information and makes it freely available, subject to the bounds of medical confidentiality, for the benefit of all those concerned with the organisation and conduct of sport diving activities, and in particular, all divers. The BSAC Incidents Reporting Scheme has been established for some 27 years, longer than some diver training organisations. It uses information gathered from a large variety of sources, including the individuals and clubs involved, H.M. Coastguard, recompression chamber operators, the Institute of Naval Medicine and a press cuttings service. All reports received are analysed and summarised in this report with the intention of highlighting any lessons that can be learnt. The BSAC uses this information to identify any trends in diving incidents in order togive its best advice and, if necessary, introduce new training prior to these trends becoming commonplace occurrences. This year (1992) there have been 123 reports received, and it is estimated that over 1.5 million 'man-dives' have been carried out. This is an apparent 30% reduction in dives carried out when compared to 1991 ,possibly due to both the depressed state of the economy and due to the inclement weather on the South Coast for most of the year. The vast majority of these dives were carried out in complete safety and attracted no publicity.
    [Show full text]
  • Dock Leveler Air-Air-Pair-Poweredpowered
    DOCK LEVELER AIR-AIR-PAIR-POWEREDPOWERED 1 aFX® DOCK LEVELER PRODUCT DETAILS Provides better stress distribution, resulting in less wear and It’s the original Kelley air-powered dock leveler that revolutionized the industry. In addition to delivering a safe, powered 1. Unique Lambda Beam Design: fatigue, longer life and less downtime for emergency maintenance. performance at a cost comparable to mechanical dock levelers, the aFX features airDefense® — preventing stump-out and providing a measure of free fall protection. The aFX is also backed by the strongest warranty in the industry, with a rated lifetime lip hinge 2. Self-Cleaning, Lug-Type Hinge: With heavy lugs welded directly to each beam and lip warranty, 10-year structural warranty and a 5-year parts and labor warranty on the lifting system, making it the preferred choice of assembly, the Kelley lug-style hinge design is the strongest in the industry. warehousing operations worldwide. 3. Durable, Reinforced Composite Lifting Bag: Lifting bag with RF welded, reinforced polyvinyl chloride coated polyester fibers operates without loss of performance in temperatures from -65°F to +200°F, even if punctured. The airbag cannot be over-inflated (maximum motor pressure is 4 PSI), and has been tested for chemical immersion and rodent damage. 2 4. Deck Support Legs with airDefense®: High efficiency 60,000 lbs. dock level support legs 9 are drop tested to the full rated capacity of the dock leveler. Special airDefense rollers glide along a reinforced cam, preventing stump-out and providing fluid, free-float motion, along with a measure of free fall protection in the event of premature trailer separation.
    [Show full text]
  • 2 & 3 Teir Lifting Bags
    2 & 3 TEIR LIFTING BAGS CONTENTS 3 2 & 3 TEIR LIFTING BAGS 5 STANDARD REGULATOR 6 ALUMINIUM CONTROLLERS 7 HANDHELD CONTROLLERS 8 HOSES 2 & 3 TIER LIFTING BAGS MFC International offer a 2 or 3 tier low pressure airlift These bags have a large contact area which means they bag designed primarily for the recovery of vehicles. The uniformly distribute lift pressure across a large surface area, tiered design allows for greater stability during the lift than making them suitable for lifting at weak points of a vehicle such conventional low pressure bags. as the roof, sides, wings, bonnet and boot. FEATURES USED FOR • Lightweight and easily portable • Road traffic incidents • Provide a strong and steady lift to stabilize a vehicle and improve access to casualties INCLUDED • Exceptionally Stable • Valise (for up to two bags) • Strong and Durable • Repair kit • Non-slip top surface • Low maintenance costs • Large lift capacity and height • Small footprint for lift height • Controlled deflation capability 3 2 & 3 TIER LIFTING BAGS 2 TIER 3 TIER Product Code LB0067 LB0068 Materials Hypalon Coated Nylon Length (cm / inch) 55 / 21.7” 55 / 21.7” Width (cm / inch) 45 / 17.7” 45 / 17.7” Inflated Height (cm / inch) 40 / 15.7” 60 / 23.6” Deflated Height (cm / inch) 5 / 2” 5 / 2” Lift at Max Pressure (kg / lbs) 2150 / 4740 1780 / 3924 Air Requirements (ltr / ft3) 110 / 3.9 150 / 5.3 Packed Weight (kg) 10 / 22 15 / 32 Max Pressure (bar /psi) 1 / 14.5 1 / 14.5 SYSTEM SCHEMATIC d a c b 1 2 3 4 Low-Pressure Supply Either from BA cylinder & regulator or a compressor
    [Show full text]
  • Draft Environmental Impact Statement
    South Fork Flathead Watershed Westslope Cutthroat Trout Conservation Program Draft Environmental Impact Statement Responsible Agency: U.S. Department of Energy (DOE), Bonneville Power Administration (BPA) Cooperating Agencies: U.S. Department of Agriculture, Forest Service (FS) and State of Montana Fish, Wildlife, and Parks (MFWP) Department Title of Proposed Project: South Fork Flathead Watershed Westslope Cutthroat Trout Conservation Program State Involved: Montana Abstract: In cooperation with MFWP, BPA is proposing to implement a conservation program to preserve the genetic purity of the westslope cutthroat trout populations in the South Fork of the Flathead drainage. The South Fork Flathead Watershed Westslope Cutthroat Trout Conservation Program constitutes a portion of the Hungry Horse Mitigation Program. The purpose of the Hungry Horse Mitigation Program is to mitigate for the construction and operation of Hungry Horse Dam through restoring habitat, improving fish passage, protecting and recovering native fish populations, and reestablishing fish harvest opportunities. The target species for the Hungry Horse Mitigation Program are bull trout, westslope cutthroat trout, and mountain whitefish. The program is designed to preserve the genetically pure fluvial and adfluvial westslope cutthroat trout (Oncorhynchus clarki lewisi) populations in the South Fork drainage of the Flathead River. In order to accomplish the goals, MFWP is proposing to remove hybrid trout from identified lakes in the South Fork Flathead drainage on the Flathead National Forest and replace them with genetically pure native westslope cutthroat trout over the next 10-12 years. Some of these lakes occur within the Bob Marshall Wilderness and Jewel Basin Hiking Area. Currently, 21 lakes and their outflow streams with hybrid populations have been identified and are included in this proposal.
    [Show full text]
  • Functional Neuromuscular Electrical Stimulation 8.03.01
    Functional Neuromuscular Electrical Stimulation 8.03.01 Functional Neuromuscular Electrical Stimulation Policy Number: 8.03.01 Last Review: 4/2021 Origination: 10/1988 Next Review: 4/2022 Blue KC has developed medical policies that serve as one of the sets of guidelines for coverage decisions. Benefit plans vary in coverage and some plans may not provide coverage for certain services discussed in the medical policies. Coverage decisions are subject to all terms and conditions of the applicable benefit plan, including specific exclusions and limitations, and to applicable state and/or federal law. Medical policy does not constitute plan authorization, nor is it an explanation of benefits. When reviewing for a Medicare beneficiary, guidance from National Coverage Determinations (NCD) and Local Coverage Determinations (LCD) supersede the Medical Policies of Blue KC. Blue KC Medical Policies are used in the absence of guidance from an NCD or LCD. Policy Blue Cross and Blue Shield of Kansas City (Blue KC) will not provide coverage for functional neuromuscular stimulation. This is considered investigational. Neuromuscular stimulation is excluded in contracts that contain an exclusion for electrical stimulation. Verify benefits to determine whether this is a benefit exclusion or investigational. When Policy Topic is covered Not Applicable When Policy Topic is not covered Neuromuscular (electrical) stimulation is considered investigational as a technique to restore function following nerve damage or nerve injury. This includes its use in the following situations: . As a technique to provide ambulation in patients with spinal cord injury; or . To provide upper extremity function in patients with nerve damage (e.g., spinal cord injury or post-stroke); or Functional Neuromuscular Electrical Stimulation 8.03.01 .
    [Show full text]
  • Scientific Diving Techniques in Restricted Overhead Environments
    doi:10.3723/ut.31.013 International Journal of the Society for Underwater Technology, Vol 31, No 1, pp 13–19, 2012 per Scientific diving techniques in restricted overhead environments *1,2 3 4 1 Giorgio Caramanna , Pirkko Kekäläinen , Jouni Leinikki and Mercedes Maroto-Valer Pa Technical 1Heriot-Watt University, Edinburgh, Scotland, UK 2Italian Association of Scientific Divers (AIOSS), Italy 3University of Helsinki, Finland 4Alleco Ltd, Finland Abstract applications (Auster et al., 1988; Auster, 1997; Scientific diving is an extremely useful tool for supporting Norcross and Mueter, 1999; Sarradin et al., 2002; research in environments with restricted access, where Bovio et al., 2006; Bowen et al., 2007), they cannot remotely operated or autonomous underwater vehicles can- always replace the presence of a scientific diver with not be used. However, these environments tend to be close regard to the quality and reliability of collected data. to the surface and require the application of advanced diving There are also environments, such as caves, under- techniques to ensure that the research is conducted within ice areas, springs or small lakes, in which access can acceptable safety parameters. The two main techniques be restricted and difficult to enter, and where use of discussed are under-ice and cave diving; for each environ- automated systems can be either complex or impos- ment the specific hazards are reviewed and methods for sible to achieve. Some of these restricted environ- mitigating the concomitant risks are detailed. It is concluded ments have related potential hazards for diving that that scientific diving operations in these environments can have to be correctly identified and addressed in be conducted to acceptable risk levels; however, risk man- agement strategies must outline precisely when and where order to guarantee that the underwater research is diving operations are to be prohibited or terminated.
    [Show full text]
  • Jacks, Industrial Rollers, Air Casters, and Hydraulic Gantries
    ASME B30.1-2015 (Revision of ASME B30.1-2009) Jacks, Industrial Rollers, Air Casters, and Hydraulic Gantries Safety Standard for Cableways, Cranes, Derricks, Hoists, Hooks, Jacks, and Slings AN AMERICAN NATIONAL STANDARD www.astaco.ir ASME B30.1-2015 (Revision of ASME B30.1-2009) Jacks, Industrial Rollers, Air Casters, and Hydraulic Gantries Safety Standard for Cableways, Cranes, Derricks, Hoists, Hooks, Jacks, and Slings AN AMERICAN NATIONAL STANDARD Two Park Avenue • New York, NY • 10016 USA www.astaco.ir Date of Issuance: May 29, 2015 The next edition of this Standard is scheduled for publication in 2020. This Standard will become effective 1 year after the Date of Issuance. ASME issues written replies to inquiries concerning interpretations of technical aspects of this Standard. Interpretations are published on the ASME Web site under the Committee Pages at http://cstools.asme.org/ as they are issued. Interpretations will also be included with each edition. Errata to codes and standards may be posted on the ASME Web site under the Committee Pages to provide corrections to incorrectly published items, or to correct typographical or grammatical errors in codes and standards. Such errata shall be used on the date posted. The Committee Pages can be found at http://cstools.asme.org/. There is an option available to automatically receive an e-mail notification when errata are posted to a particular code or standard. This option can be found on the appropriate Committee Page after selecting “Errata” in the “Publication Information” section. ASME is the registered trademark of The American Society of Mechanical Engineers.
    [Show full text]
  • Www .Savatech.Com
    www.savatech.com 1 CONTENTS HIGH-PRESSURE LIFTING BAGS 4 HIGH-PRESSURE FLAT-FORM LIFTING BAGS 6 HIGH-PRESSURE HOSE 7 MEDIUM-PRESSURE BAGS 8 MAXI-LIFT RECOVERY BAGS 9 TANK SEALING BAGS 10 PIPE SEALING BAGS 11 INFLATION ACCESSORIES 12 INFLATION ACCESSORIES 13 TANKS 14 SHELTERS - WILDERNESS RESCUE 15 Savatech Corp. 413 Oak Place, Bldg. 5J Port Orange, FL 32127 USA 888-436-9778 toll free 386-760-0706 International 386-760-8754 fax www.savatech.com [email protected] 2 APPLICATION High-pressure lifting bags For lifting the heaviest objects. Lift up to 74 tons per bag. Use these bags for sturdy objects. Use these bags for lifting, stabilizing or moving steel objects, motor vehicles, buildings, concrete or other sturdy structures. High-lift, medium-pressure lifting bags For lifting large objects or delicate structures such as aircraft, or light-weight aluminum structures. Low-pressure, high-lift, lifting bags exerte a low concentrated lifting force over a wide area. High-pressure Flat-Form lifting bags HighH lift and high capacity. The newest technology in the high-pressure liftingl bag industry. Use these bags when extra stability is desired. Higher lift can be achieved by stacking more bags. Maxi-lift recovery lifting bags For lifting the largest objects. Excellent for delicate structures such as soft-side tractor-trailers, aircraft, or light-weight aluminum structures. Low-pressure lifting bags exert low concentrated force over a wider area. Leak sealing bags For temporary leak sealing. Use for tanks, pipes, containers of all shapes and sizes. Can be used for the most hazardous liquids, fuels, water,w oils, etc.
    [Show full text]
  • Severe Hypoxemia During Apnea in Humans: Influence of Cardiovascular Responses
    From the Department of Physiology and Pharmacology Section of Environmental Physiology Karolinska Institutet Stockholm, Sweden Severe hypoxemia during apnea in humans: influence of cardiovascular responses by Peter Lindholm Stockholm 2002 ABSTRACT When a diving human holds his or her breath, the heart beat slows and the blood vessels constrict in large portions of the body. In diving mammals such as seals, similar responses effectively conserve oxygen for the brain, enabling them to dive very deep and to stay underwater for a long time. The principal aim of this thesis was to study the biological significance of bradycardia (a slowing of the heart rate) and vasoconstriction during apnea in exercising humans. The question was whether these cardiovascular mechanisms also in humans would temporarily “conserve” oxygen (i.e. temporarily reduce O2 uptake in muscles etc.) and thus protect the brain from a level of hypoxia that would otherwise cause unconsciousness in a breath-hold diver. A second aim was to determine the inter-individual variation among the human subjects in terms of the degree of bradycardia during apnea, in order to explore whether the intensity of these cardiovascular responses would make some individuals more fit to survive underwater swimming and apnea than others. Our results indeed showed inter-individual differences such that a high degree of bradycardia during apnea correlated significantly with higher levels (= better conservation) of arterial oxygen saturation. Thus, the subjects with the lowest heart rates during exercise and apnea had the best preserved saturation measured with earlobe pulse oximetry. Also, we found that the cardiovascular responses to apnea in exercising humans clearly delay the development of hypoxemia by reducing the rate of uptake from the main oxygen store, i.e.
    [Show full text]