2011 Results 2011 Résultats Canadian Senior and Intermediate
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Final Symposium 2019
Global Ideas Institute FINAL SYMPOSIUM 2019 GII PARTNERS GUEST SPEAKERS John Robinson Professor, Munk School of Global Affairs and Public Policy, School of the Environment Kris Hornburg Manager, Program & Strategic Initiatives, Solid Waste Management Services, City of Toronto Garima Tilokani Graduate Student, Munk School of Global Affairs and Public Policy Hannah Rundle Graduate Student, Munk School of Global Affairs and Public Policy Juliana Forner Graduate Student, Munk School of Global Affairs and Public Policy Joshua Folkema Business Development Manager, Canada World Vision Joseph Wong Founder, Global Ideas Institute Benjamin Scott Technology Manager, GreenMantra Technologies Asif Raza Manager of Engineering, GreenMantra Technologies Dilip Solman Canada Research Chair in Behavioral Science and Economics, Rotman School of Management Welcome to the GLOBAL IDEAS INSTITUTE In our global economy, it is becoming increasingly of plastic packaging waste per capita. The many important for students to learn about the world and benefits of plastic are undeniable. The material is to think in a global context. This cutting-edge cheap, lightweight, easy to make, and versatile, with program provides students with the tools, innumerable applications. These same properties knowledge, and guidance to develop innovative have led to a boom in the production of plastic over solutions to complex world issues. Over the course the past century, a trend that is projected to of the year, students gain exposure to leading global skyrocket over the next 10 to 15 years. However, experts, develop complex problem-solving skills, due to the durability of the material and because and deliver pitches to a panel of distinguished most plastic do not biodegrade, it makes it experts. -

1986 C 1 51-1 06/12/B5 1
• I i Clause Report FI Ie Page ~ ~~NO. ~ 1. APPO I NTMENT OF ALDERMEN TO REPRESENT THE CITY OF NORTH YORK ()'~ METRO TORONTO OOUNCI L C 51-1 06/12/B5 2. APPOINTMENT OF STANDING COMMITTEES OF COUNCIL FOR THE PERIOD FROM DEC. 1/85 TO NOV. 30/86 C 51-1 06/12/B5 3. ENACT BY-LAW 29763 TO VARY THE COMPOSITION OF THE PLANNING ADVISORY COMMITTEE C 51-1 06/12/85 4. APPOINTMENT OF MEMBERS OF COUNCIL TO VARIOUS OTHER BOARDS AND COMMITTEES FOR THE PERIOD DEC. I/B5 TO NOV. 30/B6 C 51-1 06/12/85 5. ENACT BY-LAW 29764 TO APPOINT ALDERMAN B. BURTON AS A SUBSTITUTE FOR THE MAYOR ON THE N.YK. PUBLIC LIBRARY BOARD FOR THE YEAR 1986 C 1 51-1 06/12/B5 1. Z-B5-61 - BRUNO FATTORE - lB3 & 185 JOICEY BLVD. WARD 6 C 2 86 16/12/85 2. DPZ-85-62 - W. WITHROW AND I. SEARLE - 90-96 ELLERSLIE AVENUE. WARD 9 C 2 86 16/12/85 3. DPZ-85-63 - ROCCO GROSS I GROUP CONSTRUCTI ON LTD. - 20 PR IVET ROAD. WAAD 2 C 2 86 16/121B5 4. DPZ-85-64 - SERVOCRAFT LIMITED - SOUTH-EAST CORNER OF LAWRENCE AVENUE WET AND BLACK CREEK DRIVE. WAAD 2 C 2 86 16/12/85 5. Z-B5-65 - THE GLEN GROUP - 5050 DUFFERIN STREET - WEST SIDE DUFFERIN STREET, NORTH OF DOLOMITE DRIVE. WARD 7 C 2 86 16/12/85 6. Z-B5-66 - SERBINSKI & ASSOCIATES INC. - 183 SHEPPARD AVENUE WEST. -

2020/21 Annual Report 2020/21 Annual Table of Contents Report
2020/21 Annual Report 2020/21 Annual Table of Contents Report Board 2020/21 1 Board Nomination 3 President’s Message 4 Treasurer’s Report 6 Marketing & Communications 8 Events 9 2020/21 Event Highlights 12 Our Members 14 About NISPA 15 2020/21 Annual Report 2020/21 Annual 2020/21 Board Report Page 1 Krystie Robinson-Vincent Connie Castillo PRESIDENT Montcrest School Pickering College Jackie Sklenka Domenica Coppa The York School & Crescent School VICE PRESIDENT Holy Trinity School Nancy Nash The York School Kerstin Lueck St. Michael’s College School PAST PRESIDENT (Ex-Officio) The York School Tanya Giaquinto Appleby College Susan Ianni St. Michael’s College School TREASURER Holy Trinity School Patricia A. Graham St. Michael’s College School Kathy Vucic De La Salle College (Oaklands) SECRETARY Appleby College Rachel O’Donovan St. John’s-Kilmarnock School 2020/21 Annual Report Page 2 Thank You to our Board members who are moving on: Connie Castillo Kerstin Lueck Nancy Nash Patricia Graham Rachel O’Donovan It has been amazing having you all on the team! Thank you for your dedication, commitment and all for that you have done to help NISPA succeed over the years. Your contributions over the years have been invaluable! 2020/21 Annual 2021–2022 Board Nominations Report Page 3 NISPA’s Nomination Committee is pleased to present a slate of Board members for election at the upcoming Annual General Meeting on May 26, 2021. Nominees Chair Domenica Coppa Vice Chair Tanya Giaquinto Treasurer Susan Ianni Secretary Kathy Vucic Director Jackie Sklenka Nicol Andrea Domingues Jo Hanna Ex-Officio Past President Krystie Robinson-Vincent 2020/21 Annual President’s Message Report Page 4 With hopes of returning to our much anticipated in-person networking events, this year at NISPA we remained focused on keeping our members safe and continued to concentrate our attention on providing engaging, interactive, and informative events using our virtual platforms. -

University of Toronto 2005 National Biology Competition HONOUR ROLL
University of Toronto 2005 National Biology Competition HONOUR ROLL There were 6319 eligible contestants from 453 schools. The top 50 (plus those tied with the 50th) are National Biology Scholars with Distinction. The next 200 (plus those tied with the 250th) are National Biology Scholars. Tied contestants are listed in alphabetical order. * The Top 75 Schools are listed on pages 8 and 9. NATIONAL BIOLOGY SCHOLARS WITH DISTINCTION Rank Name School 1 Charles Hache Kennebecasis Valley HS, Quispamsis, NB 2 Zexi Wang Fort Richmond Collegiate, Winnipeg, MB 3 Andrew Holt St. Matthew HS, Ottawa, ON 4 Ioana Ivan Don Mills CI, Don Mills, ON 5 Ryan Pratt St. Francis HS, Calgary, AB 6 John Rozehnal Upper Canada College, Toronto, ON 7-8 Jenny Hsi Burnaby North SS, Burnaby, BC 7-8 Shannon Refvik Fort Richmond Collegiate, Winnipeg, MB 9 Merlin Lo Burnaby North SS, Burnaby, BC 10-11 Mengzhu Jiang Victoria Park SS, North York, ON 10-11 Elizabeth Joyce Kennebecasis Valley HS, Quispamsis, NB 12-14 Kawther Hamed Mindview Academy, Pickering , ON 12-14 Alex Leong St. George’s School, Vancouver, BC 12-14 Hann-Shuin Yew The Harker School, San Jose, CA, USA 15 Kristen Sabourin St. Francis HS, Calgary, AB 16 Brienne McKenzie Trinity College School, Port Hope, ON 17 Justin Chakma Waterloo CI, Waterloo, ON 18 Linda Yuan Old Scona Academic School, Edmonton, AB 19-21 James Huang Harry Ainlay HS, Edmonton, AB 19-21 Jun Wang Bell HS, Nepean, ON 19-21 Christopher Yau University of Toronto Schools, Toronto, ON 22 Richard Oosthuizen St. Andrew’s College, Aurora, ON 23 -

Bayview Glen Independent School Annual Report
Bayview Glen Independent School Annual Report Bayview Table of Contents Glen Independent Message from Athletics School 5 Head of School 38 Alumni Relations 6 Board of Directors 44 Volunteerism 2015/2016 16 Round Square 46 Class of 2016 24 Advancement 48 Annual Advanced Placement 30 Finance 50 Scholars Report 36 The Arts 2015/2016 ANNUAL REPORT Message from Head of School Eileen Daunt y any measure, the 2016 school year was a resounding Our Grads also accumulated thousands of dollars in scholarships, success and continued to build Bayview Glen’s reputation with one of our students being awarded one of only two $10,000 for excellence. scholarship from the Rotman School of Business. BWe launched our new branding focussed on connector We continued to focus on developing our Global Citizen with our words. These words were carefully chosen to reflect who we are as Round Square exchanges, service projects at home and abroad, a school today. We were thrilled with the launch of our new website and participation in the international conferences in Germany and and Prospectus, both of which reflect the new face of Bayview Glen. Singapore. In other student achievements, our Gryphons were unstoppable, winning 51 team medals. In the Arts, our annual CISMF In 2016, Bayview Glen also unveiled its new Strategic Framework: Concert, our theatre production METAMORPHOSES, and Art Exhibit Inspiring Global Citizens and an Entrepreneurial Mindset, Enabling and Auction ALTERED, and the amazing Spring Festivals were Excellence in Learning, as well as, Connecting our Community and resounding successes. Winning a coveted spot on the Ontario Team Building Sustainability for Future Generations. -

Annual Report
2016 2017 Annual Report Bayview Glen Independent School 5 • Message from Head of School 6 • Strategic Framework 2016/2017 Annual Report 11 • Board of Directors 20 • Alumni Association Board 22 • Finance 26 • Athletics Table of Contents 32 • The Arts 34 • Digital Fluency in the 21st Century 36 • Bayview Glen Camp 38 • Parent Association 40 • Class of 2017 42 • Advancement 44 • Donor Recognition Beehive on the Moatfield rooftop garden 48 • Advanced Placement Scholars 5 elcome to the Annual Report for the 2016-2017 school year. They compiled it all into one slideshow; 26 different things were As we navigate our way through the 2017-2018 year and acknowledged and presented during their Canada 150 Assembly. Wprepare for the upcoming year, casting our minds back is worthwhile. It allows us the opportunity to revisit all the triumphs of In athletics, our Gryphons were unstoppable, amassing an amazing 2016-2017 and celebrate the amazing success once again. 58 medals altogether – 32 Gold CISAA banners, 9 Silver and 18 Bronze. Go Grrryphons! Leading the way was the Class of 2017. 47% of this class consisted of lifetime BVG students. 88% of this amazing class also challenged 223 Added to this was our Ctrl-Z World Robotics Championship and our AP exams. 100% of our graduates were accepted into post-secondary M.I.T. BioBuilders Club Bee Project. During the summer of 2017, our institutions of choice and amassed an astounding $600,000 in bees were actively pollinating and making honey on our beautiful scholarships, including Presidential, Dean’s and Faculty Scholarships rooftop patio. In September, together with our urban beekeeping at several universities. -

Bayview Glen CFO Posting
Client Organization: Bayview Glen School Position Title: Chief Financial Officer Reports to: Head of School Location: Toronto, Ontario “WHOLE CHILD, WHOLE LIFE, WHOLE WORLD” T H E SCHOOL Bayview Glen School is a progressive and innovative independent school focused on developing the whole child with a whole world view. Bayview Glen’s graduates stand out as adaptable, responsible and connected global citizens, and the School provides opportunities for a unique learning experience, developing in students the creativity, entrepreneurial mindset and capacity for innovation they need to succeed throughout their whole life. A non-profit, coeducational day school with more than 1000 students from Preschool through to Grade 12, Bayview Glen offers a truly transformative educational experience, intentionally creating a welcoming, vibrantly diverse community, guided by inspiring teachers and fueled by a forward-looking curriculum. Academically invigorating and internationally connected, Bayview Glen’s advanced inquiry- based academic program is balanced with a strong music and arts program, languages, physical education, Outdoor Adventure, and Duke of Edinburgh Programme; and co-curricular activities including an art festival, drama productions, choirs, bands, and extensive team sports. As a member of Round Square, students have a strong focus on international understanding and participate regularly in community service and character-building life experiences, locally and abroad. T H E R O L E The Chief Financial Officer is responsible to oversee and be accountable for the current and long-term effectiveness of the School’s operations functions, including Finance and Facilities. This position ensures the financial health of the School and is accountable for the overall integrity and protection of its financial records. -

923466Magazine1final
www.globalvillagefestival.ca Global Village Festival 2015 Publisher: Silk Road Publishing Founder: Steve Moghadam General Manager: Elly Achack Production Manager: Bahareh Nouri Team: Mike Mahmoudian, Sheri Chahidi, Parviz Achak, Eva Okati, Alexander Fairlie Jennifer Berry, Tony Berry Phone: 416-500-0007 Email: offi[email protected] Web: www.GlobalVillageFestival.ca Front Cover Photo Credit: © Kone | Dreamstime.com - Toronto Skyline At Night Photo Contents 08 Greater Toronto Area 49 Recreation in Toronto 78 Toronto sports 11 History of Toronto 51 Transportation in Toronto 88 List of sports teams in Toronto 16 Municipal government of Toronto 56 Public transportation in Toronto 90 List of museums in Toronto 19 Geography of Toronto 58 Economy of Toronto 92 Hotels in Toronto 22 History of neighbourhoods in Toronto 61 Toronto Purchase 94 List of neighbourhoods in Toronto 26 Demographics of Toronto 62 Public services in Toronto 97 List of Toronto parks 31 Architecture of Toronto 63 Lake Ontario 99 List of shopping malls in Toronto 36 Culture in Toronto 67 York, Upper Canada 42 Tourism in Toronto 71 Sister cities of Toronto 45 Education in Toronto 73 Annual events in Toronto 48 Health in Toronto 74 Media in Toronto 3 www.globalvillagefestival.ca The Hon. Yonah Martin SENATE SÉNAT L’hon Yonah Martin CANADA August 2015 The Senate of Canada Le Sénat du Canada Ottawa, Ontario Ottawa, Ontario K1A 0A4 K1A 0A4 August 8, 2015 Greetings from the Honourable Yonah Martin Greetings from Senator Victor Oh On behalf of the Senate of Canada, sincere greetings to all of the organizers and participants of the I am pleased to extend my warmest greetings to everyone attending the 2015 North York 2015 North York Festival. -

2008 Results Pascal Contest Cayley Contest Fermat Contest 2008
Canadian Concours Mathematics canadien de Competition math´ematiques An activity of the Centre for Une activit´edu Centre d’´education Education in Mathematics and Computing, en math´ematiques et en informatique, University of Waterloo, Waterloo, Ontario Universit´ede Waterloo, Waterloo, Ontario 2008 2008 Results R´esultats Pascal Contest Concours Pascal (Grade 9) (9e ann´ee– Sec. III) Cayley Contest Concours Cayley (Grade 10) (10e ann´ee– Sec. IV) Fermat Contest Concours Fermat (Grade 11) (11e ann´ee– Sec. V) C.M.C. Sponsors C.M.C. Supporter Chartered Accountants c 2008 Centre for Education in Mathematics and Computing Competition Organization Organisation du Concours Centre for Education in Mathematics and Computing Faculty and Staff / Personnel du Concours canadien de math´ematiques Ed Anderson Lloyd Auckland Terry Bae Janet Baker Steve Brown Jennifer Couture Fiona Dunbar Jeff Dunnett Mike Eden Barry Ferguson Judy Fox Sandy Graham Angie Hildebrand Judith Koeller Joanne Kursikowski Dean Murray J.P. Pretti Linda Schmidt Kim Schnarr Jim Schurter Carolyn Sedore Ian VanderBurgh Troy Vasiga 2 Competition Organization Organisation du Concours Problems Committees / Comit´esdes probl`emes Pascal Contest / Concours Pascal Wally Webster (Chair / pr´esident), Exeter, ON Lloyd Auckland, Waterloo, ON Janet Christ, Walter Murray C.I., Saskatoon, SK Nerissa Coronel, St. Marguerite d’Youville C.S.S., Brampton, ON JP Pretti, University of Waterloo, Waterloo, ON Jim Schurter, University of Waterloo, Waterloo, ON Tyler Somer, Kitchener, ON Anna Spanik, -

Fibonacci 2019 STUDENT HONOUR ROLL - CANADA 2019-05-12 PALMARÈS DES ÉLEVES - CANADA
Fibonacci 2019 STUDENT HONOUR ROLL - CANADA 2019-05-12 PALMARÈS DES ÉLEVES - CANADA 13984 Students have participated \ Elèves ont participé Rank Student School City Province Score Rang Élève École Ville Province Note 1 LU ISAAC GLEN SHIELDS P.S. CONCORD ON 40 1 SAJWANI AHSAN CROSBY HEIGHTS P.S. RICHMOND HILL ON 40 1 TONG MATTHEW UPPER CANADA COLLEGE TORONTO ON 40 1 ZHANG KENNY CROSBY HEIGHTS P.S. RICHMOND HILL ON 40 1 DADASHZADEH DANIEL E.E.P.JULIE PAYETTE KANATA ON 40 1 GAUTHIER EMY ECOLE DES TROIS-TEMPS (SWL) ST-LIN-LAURENTI QC 40 1 CHEN PATRICK IVY PATH SCHOOL TORONTO ON 40 1 WANG ZHENG ELITE COLLEGE MONTREAL QC 40 1 HONG JINYANG ROTHERGLEN OAKVILLE ON 40 1 BIGRAS ROSE ECOLE DES TROIS-TEMPS (SWL) ST-LIN-LAURENTI QC 40 1 BLONDIN SAMUEL ECOLE DES TROIS-TEMPS (SWL) ST-LIN-LAURENTI QC 40 1 ZHANG ANDY DENLOW P.S. TORONTO ON 40 1 AUGER PERRON ALEXANDRA ECOLE DES TROIS-TEMPS (SWL) ST-LIN-LAURENTI QC 40 1 TREMBLAY MOLIE ECOLE DES TROIS-TEMPS (SWL) ST-LIN-LAURENTI QC 40 1 BEI ER VBE (MACC) VANCOUVER BC 40 1 PLUTA ANDREI SPIRIT OF MATH (OAKV) MISSISSAUGA ON 40 1 WALTER KERI KITCHENER-WATERLOO B.S. WATERLOO ON 40 1 XING HARVEY ST.JOHN BREBEUF WINNIPEG MB 40 1 THERIAULT LAURENCE ECOLE DES TROIS-TEMPS (SWL) ST-LIN-LAURENTI QC 40 1 ZHU TONY OLYMPIADS SCHOOL NORTH YORK ON 40 1 MARGOLIS SHANNA DENLOW P.S. TORONTO ON 40 22 HE ASHER JESSIE WOWK E.S. RICHMOND BC 39 22 HUA JOYANN W.D.FERRIS E.S. -

2013 Canadian Computing Competition Results
2013 Canadian Computing Competition Results Sponsor: 1 Comments Commentaires The 2013 CCC was another year of change. In a way similar to 2012, the averages this year were very good, reinforcing that both the Junior and Senior competitions are approachable for the majority of students. Again, there is a large clump of Junior competitors who acheived 60/75, which is a very good score. We launched a live version of the on-line CCC grader (expanding from the pilot version in 2012) that about half of the competitors registered for this year. With a few glitches now sorted out (including Java memory errors and timing issues), I think the on-line grader will become the de-facto standard for contest writers, due to the feedback it provides. We will still allow teachers and students to choose to grade off-line, but the selection of languages (C, C++, Pascal, Java, Python, Perl and PHP) will hopefully cover the vast majority of competitors. Again, if students want to learn Python, check out the CS Cirlces On-line Resource at: cscircles.cemc.uwaterloo.ca We continued the collaboration with Tsinghua University in Beijing and the University of Hong Kong to offer the contest to Beijing and Hong Kong high school students. More information (including results) can be found at: http://ccc.cs.tsinghua.edu.cn/ and http://www.cs.hku.hk/ccc2013/. As in previous years, the organizers from Tsinghua and HKU collaborated with UW to create a contest different than the Canadian CCC. Below, a qualitative summary of both the Junior and Senior contest is presented. -
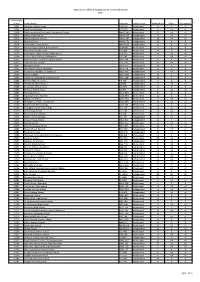
2009 Admissions Cycle
Applications, Offers & Acceptances by UCAS Apply Centre 2009 UCAS Apply Centre School Name Postcode School Sector Applications Offers Acceptances 10001 Ysgol Syr Thomas Jones LL68 9TH Maintained <4 0 0 10002 Ysgol David Hughes LL59 5SS Maintained 4 <4 <4 10008 Redborne Upper School and Community College MK45 2NU Maintained 5 <4 <4 10010 Bedford High School MK40 2BS Independent 7 <4 <4 10011 Bedford Modern School MK41 7NT Independent 18 <4 <4 10012 Bedford School MK40 2TU Independent 20 8 8 10014 Dame Alice Harpur School MK42 0BX Independent 8 4 <4 10018 Stratton Upper School, Bedfordshire SG18 8JB Maintained 5 0 0 10020 Manshead School, Luton LU1 4BB Maintained <4 0 0 10022 Queensbury Upper School, Bedfordshire LU6 3BU Maintained <4 <4 <4 10024 Cedars Upper School, Bedfordshire LU7 2AE Maintained 7 <4 <4 10026 St Marylebone Church of England School W1U 5BA Maintained 8 4 4 10027 Luton VI Form College LU2 7EW Maintained 12 <4 <4 10029 Abingdon School OX14 1DE Independent 15 4 4 10030 John Mason School, Abingdon OX14 1JB Maintained <4 0 0 10031 Our Lady's Abingdon Trustees Ltd OX14 3PS Independent <4 <4 <4 10032 Radley College OX14 2HR Independent 15 7 6 10033 The School of St Helen & St Katharine OX14 1BE Independent 22 9 9 10035 Dean College of London N7 7QP Independent <4 0 0 10036 The Marist Senior School SL57PS Independent <4 <4 <4 10038 St Georges School, Ascot SL5 7DZ Independent <4 0 0 10039 St Marys School, Ascot SL5 9JF Independent 6 <4 <4 10041 Ranelagh School RG12 9DA Maintained 8 0 0 10043 Ysgol Gyfun Bro Myrddin SA32 8DN Maintained