2008 2008 Results R´Esultats
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

2011 Results 2011 Résultats Canadian Senior and Intermediate
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING Le CENTRE d'EDUCATION´ en MATHEMATIQUES´ et en INFORMATIQUE www.cemc.uwaterloo.ca 2011 2011 Results R´esultats Canadian Senior and Intermediate Mathematics Contests Concours canadiens de math´ematiques de niveau sup´erieuret interm´ediaire c 2012 University of Waterloo Competition Organization Organisation du Concours Centre for Education in Mathematics and Computing Faculty and Staff / Personnel du Concours canadien de math´ematiques Ed Anderson Terry Bae Steve Brown Ersal Cahit Karen Cole Serge D'Alessio Frank DeMaio Jennifer Doucet Fiona Dunbar Mike Eden Barry Ferguson Barb Forrest Judy Fox Steve Furino John Galbraith Sandy Graham Angie Hildebrand Judith Koeller Joanne Kursikowski Bev Marshman Dean Murray Jen Nissen J.P. Pretti Linda Schmidt Kim Schnarr Jim Schurter Carolyn Sedore Ian VanderBurgh Troy Vasiga Problems Committees / Comit´esdes probl`emes Canadian Senior Mathematics Contest / Concours canadien de niveau sup´erieur Mike Eden (Chair / pr´esident), University of Waterloo, Waterloo, ON Kee Ip, Crescent School, Toronto, ON Paul Leistra, Guido de Bres Christian H.S., Hamilton, ON Daryl Tingley, University of New Brunswick, Fredericton, NB Joe West, University of Waterloo, Waterloo, ON Bruce White, Windsor, ON Canadian Intermediate Mathematics Contest / Concours canadien de niveau interm´ediaire John Galbraith (Chair / pr´esident), University of Waterloo, Waterloo, ON Ed Barbeau, Toronto, ON Alison Cornthwaite, Lo-Ellen Park S.S., Sudbury, ON Brian McBain, North Lambton S.S., Forest, ON Ginger Moorey, Abbey Park H.S., Oakville, ON Dean Murray, University of Waterloo, Waterloo, ON 2 Foreword Avant-Propos The Centre for Education in Mathematics and Computing is pleased to announce the results of the 2011 Canadian Senior and Intermediate Mathematics Contests. -

2008 Results Pascal Contest Cayley Contest Fermat Contest 2008
Canadian Concours Mathematics canadien de Competition math´ematiques An activity of the Centre for Une activit´edu Centre d’´education Education in Mathematics and Computing, en math´ematiques et en informatique, University of Waterloo, Waterloo, Ontario Universit´ede Waterloo, Waterloo, Ontario 2008 2008 Results R´esultats Pascal Contest Concours Pascal (Grade 9) (9e ann´ee– Sec. III) Cayley Contest Concours Cayley (Grade 10) (10e ann´ee– Sec. IV) Fermat Contest Concours Fermat (Grade 11) (11e ann´ee– Sec. V) C.M.C. Sponsors C.M.C. Supporter Chartered Accountants c 2008 Centre for Education in Mathematics and Computing Competition Organization Organisation du Concours Centre for Education in Mathematics and Computing Faculty and Staff / Personnel du Concours canadien de math´ematiques Ed Anderson Lloyd Auckland Terry Bae Janet Baker Steve Brown Jennifer Couture Fiona Dunbar Jeff Dunnett Mike Eden Barry Ferguson Judy Fox Sandy Graham Angie Hildebrand Judith Koeller Joanne Kursikowski Dean Murray J.P. Pretti Linda Schmidt Kim Schnarr Jim Schurter Carolyn Sedore Ian VanderBurgh Troy Vasiga 2 Competition Organization Organisation du Concours Problems Committees / Comit´esdes probl`emes Pascal Contest / Concours Pascal Wally Webster (Chair / pr´esident), Exeter, ON Lloyd Auckland, Waterloo, ON Janet Christ, Walter Murray C.I., Saskatoon, SK Nerissa Coronel, St. Marguerite d’Youville C.S.S., Brampton, ON JP Pretti, University of Waterloo, Waterloo, ON Jim Schurter, University of Waterloo, Waterloo, ON Tyler Somer, Kitchener, ON Anna Spanik, -

2013 Canadian Computing Competition Results
2013 Canadian Computing Competition Results Sponsor: 1 Comments Commentaires The 2013 CCC was another year of change. In a way similar to 2012, the averages this year were very good, reinforcing that both the Junior and Senior competitions are approachable for the majority of students. Again, there is a large clump of Junior competitors who acheived 60/75, which is a very good score. We launched a live version of the on-line CCC grader (expanding from the pilot version in 2012) that about half of the competitors registered for this year. With a few glitches now sorted out (including Java memory errors and timing issues), I think the on-line grader will become the de-facto standard for contest writers, due to the feedback it provides. We will still allow teachers and students to choose to grade off-line, but the selection of languages (C, C++, Pascal, Java, Python, Perl and PHP) will hopefully cover the vast majority of competitors. Again, if students want to learn Python, check out the CS Cirlces On-line Resource at: cscircles.cemc.uwaterloo.ca We continued the collaboration with Tsinghua University in Beijing and the University of Hong Kong to offer the contest to Beijing and Hong Kong high school students. More information (including results) can be found at: http://ccc.cs.tsinghua.edu.cn/ and http://www.cs.hku.hk/ccc2013/. As in previous years, the organizers from Tsinghua and HKU collaborated with UW to create a contest different than the Canadian CCC. Below, a qualitative summary of both the Junior and Senior contest is presented. -
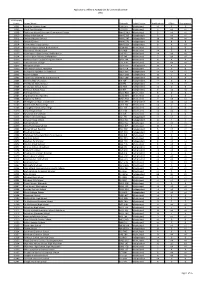
2009 Admissions Cycle
Applications, Offers & Acceptances by UCAS Apply Centre 2009 UCAS Apply Centre School Name Postcode School Sector Applications Offers Acceptances 10001 Ysgol Syr Thomas Jones LL68 9TH Maintained <4 0 0 10002 Ysgol David Hughes LL59 5SS Maintained 4 <4 <4 10008 Redborne Upper School and Community College MK45 2NU Maintained 5 <4 <4 10010 Bedford High School MK40 2BS Independent 7 <4 <4 10011 Bedford Modern School MK41 7NT Independent 18 <4 <4 10012 Bedford School MK40 2TU Independent 20 8 8 10014 Dame Alice Harpur School MK42 0BX Independent 8 4 <4 10018 Stratton Upper School, Bedfordshire SG18 8JB Maintained 5 0 0 10020 Manshead School, Luton LU1 4BB Maintained <4 0 0 10022 Queensbury Upper School, Bedfordshire LU6 3BU Maintained <4 <4 <4 10024 Cedars Upper School, Bedfordshire LU7 2AE Maintained 7 <4 <4 10026 St Marylebone Church of England School W1U 5BA Maintained 8 4 4 10027 Luton VI Form College LU2 7EW Maintained 12 <4 <4 10029 Abingdon School OX14 1DE Independent 15 4 4 10030 John Mason School, Abingdon OX14 1JB Maintained <4 0 0 10031 Our Lady's Abingdon Trustees Ltd OX14 3PS Independent <4 <4 <4 10032 Radley College OX14 2HR Independent 15 7 6 10033 The School of St Helen & St Katharine OX14 1BE Independent 22 9 9 10035 Dean College of London N7 7QP Independent <4 0 0 10036 The Marist Senior School SL57PS Independent <4 <4 <4 10038 St Georges School, Ascot SL5 7DZ Independent <4 0 0 10039 St Marys School, Ascot SL5 9JF Independent 6 <4 <4 10041 Ranelagh School RG12 9DA Maintained 8 0 0 10043 Ysgol Gyfun Bro Myrddin SA32 8DN Maintained -

Toronto Regional Showcase 2017
Toronto Regional Showcase 2017 April 6, 7 and 8 Hart House Theatre University of Toronto Page 1 Welcomes you to the Regional Showcase of the 71st Annual Sears Ontario Drama Festival! Sears Canada is proud to sponsor this exceptional event and to celebrate remarkable achievements in the arts by talented students, such as those you will see on the stage this evening. These performances are a reflection of the dedicated and talented students and teachers in the drama programs of our Ontario high schools. The Sears Charitable Foundation is a registered Canadian charity focused on the development of children and youth in areas of both health and education. The health component is centered on raising awareness and providing funds for research and treatment for the fight against childhood cancer. The education component is centered on after-school programs and initiatives such as the Sears Ontario Drama Festival, which enrich young people’s lives and allow them to reach their full potential. Please consider making a donation and help us continue to provide meaningful experiences. Together, we can make a difference in the lives of young people. Visit www.searsfoundation.ca Page 2 Welcome... to the 71st Toronto Regional Showcase of the Sears Ontario Drama Festival. The nine productions that you will see during the three evenings of the Showcase represent outstanding achievement in high school theatre from the three Toronto District Festivals. The presentations are accompanied by public and private adjudications that expand the participating students’ -

Applications, Offers & Acceptances by UCAS Apply Centre
Applications, Offers & Acceptances by UCAS Apply Centre 2015 UCAS Apply School Name Postcode School Sector Applications Offers Acceptances Centre 10001 Ysgol Syr Thomas Jones LL68 9TH Maintained <3 <3 <3 10002 Ysgol David Hughes LL59 5SS Maintained 5 <3 <3 10006 Ysgol Gyfun Llangefni LL77 7NG Maintained <3 <3 <3 10008 Redborne Upper School and Community College MK45 2NU Maintained 3 <3 <3 10011 Bedford Modern School MK41 7NT Independent 19 4 4 10012 Bedford School MK40 2TU Independent 8 <3 <3 10018 Stratton Upper School, Bedfordshire SG18 8JB Maintained 3 <3 <3 10019 Dunstable College LU5 4HG Maintained <3 <3 <3 10020 Manshead School, Luton LU1 4BB Maintained <3 <3 <3 10024 Cedars Upper School, Bedfordshire LU7 2AE Maintained 3 <3 <3 10026 St Marylebone Church of England School W1U 5BA Maintained 6 <3 <3 10027 Luton VI Form College LU2 7EW Maintained 6 3 3 10029 Abingdon School OX14 1DE Independent 19 4 4 10030 John Mason School, Abingdon OX14 1JB Maintained 3 <3 <3 10032 Radley College OX14 2HR Independent 9 3 3 10033 St Helen & St Katharine OX14 1BE Independent 10 5 4 10034 Heathfield School, Berkshire SL5 8BQ Independent <3 <3 <3 10036 The Marist Senior School SL5 7PS Independent <3 <3 <3 10038 St Georges School, Ascot SL5 7DZ Independent <3 <3 <3 10039 St Marys School, Ascot SL5 9JF Independent 12 5 5 10041 Ranelagh School RG12 9DA Maintained <3 <3 <3 10042 Bracknell and Wokingham College RG12 1DJ Maintained <3 <3 <3 10043 Ysgol Gyfun Bro Myrddin SA32 8DN Maintained <3 <3 <3 10044 Edgbarrow School RG45 7HZ Maintained <3 <3 <3 10045 -

IBM Centers for Advanced Studies : CASCON
Country/region [ select ] Home Business solutions IT services Products Support & downloads My IBM CAS Worldwide Homepage Overview Technology Showcase Technical Papers Workshops Schedule at a Glance Speakers by Day CASCON technology showcase CASCON technical papers An amazing range of technology innovations as The technical papers program features experience well as a showcase of research results. Come to reports and original research papers. Best Paper browse the displays and talk to developers and and Best Student Paper awards will be presented Registration is now closed. CASCON 2009 will take place researchers from industry and academia. at Tuesday morning's keynote session. on November 2-5. Learn more Learn more CASCON 2008 Highlights Highlights and video on CASCON speakers ITWorldCanada CASCON workshops Keynote and Frontiers of Software Practice More info From hands-on learning to tutorials to panel presentations by innovators and thought-leaders discussions, CASCON workshops give you a great on topics of world-changing impact. Don't miss Read the highlights article opportunity to acquire new skills and participate in them! View (28kb) lively discussions. Learn more Get Adobe® Reader® Learn more Navigation and resources CASCON 2008 Resources Related links CASCON events CASCON 2008 Videos Registration & sign-in Hotel information IBM University Relations CASCONcamp demo camp Watch full-length videos from Full papers Sponsors Programming Contest High school competition the conference CASCON 2008 Program Contacts Central Click here Committee -

2012 Canadian Computing Competition Results
2012 Canadian Computing Competition Results Sponsor: 1 Comments Commentaires The 2012 CCC was a year of expansions, simplifications and new initiatives. In terms of expansions, the registrations for the CCC increased by 20the last few years. Thanks to all of those participants, both new and returning. In terms of simplifications, the averages on the contest were much higher, since we intended to make the contests much more approachable, both in the Junior and Senior categories. Overall, I am happy that so many Junior students got a score of 60/75 or better. You will see a large “clump” of results in Group 4 of the Junior results. In other words, don’t print this document on paper unless you really need to! In terms of new initiatives, 2012 (and late 2011) saw a few firsts. The CEMC undertook the Beaver Computing Competition (BCC), which is intended to get interested math students to consider trying out programming. We have also launched “CS Circles”, which is a way to learn Python, which would be a very good language to program the CCC in. And, finally, we launched a pilot version of the on-line CCC grader that many of the Senior competitors tried out this year. We will be launching a Canada-wide version in Fall 2012, both for practice and for writing the actual CCC in Feburary 2013. All of these new items can be found at: www.cemc.uwaterloo.ca We continued the collaboration with Tsinghua University in Beijing and the University of Hong Kong to offer the contest to Beijing and Hong Kong high school students. -
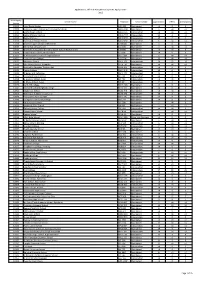
2012 Admissions Cycle
Applications, Offers & Acceptances by UCAS Apply Centre 2012 UCAS Apply School Name Postcode School Sector Applications Offers Acceptances Centre 10002 Ysgol David Hughes LL59 5SS Maintained <4 0 0 10008 Redborne Upper School and Community College MK45 2NU Maintained 5 <4 <4 10010 Bedford High School MK40 2BS Independent <4 <4 <4 10011 Bedford Modern School MK41 7NT Independent 15 4 <4 10012 Bedford School MK40 2TU Independent 15 4 4 10014 Dame Alice Harpur School MK42 0BX Independent 6 <4 <4 10018 Stratton Upper School, Bedfordshire SG18 8JB Maintained 4 0 0 10020 Manshead School, Luton LU1 4BB Maintained 4 <4 <4 10022 Queensbury Academy (formerly Upper School) Bedfordshire LU6 3BU Maintained <4 <4 0 10024 Cedars Upper School, Bedfordshire LU7 2AE Maintained <4 0 0 10026 St Marylebone Church of England School W1U 5BA Maintained 6 <4 <4 10027 Luton VI Form College LU2 7EW Maintained 15 <4 <4 10029 Abingdon School OX14 1DE Independent 26 13 10 10030 John Mason School, Abingdon OX14 1JB Maintained <4 <4 <4 10031 Our Lady's Abingdon Trustees Ltd OX14 3PS Independent <4 0 0 10032 Radley College OX14 2HR Independent 18 6 5 10033 St Helen & St Katharine OX14 1BE Independent 14 4 <4 10036 The Marist Senior School SL5 7PS Independent <4 0 0 10038 St Georges School, Ascot SL5 7DZ Independent <4 <4 0 10039 St Marys School, Ascot SL5 9JF Independent 7 4 4 10040 Garth Hill College RG42 2AD Maintained <4 0 0 10042 Bracknell and Wokingham College RG12 1DJ Maintained <4 0 0 10044 Edgbarrow School RG45 7HZ Maintained <4 <4 0 10045 Wellington College, -

2013 Canadian Computing Competition Results
2013 Canadian Computing Competition Results Sponsors: 1 Comments Commentaires The 2013 CCC was another year of change. In a way similar to 2012, the averages this year were very good, reinforcing that both the Junior and Senior competitions are approachable for the majority of students. Again, there is a large clump of Junior competitors who acheived 60/75, which is a very good score. We launched a live version of the on-line CCC grader (expanding from the pilot version in 2012) that about half of the competitors registered for this year. With a few glitches now sorted out (including Java memory errors and timing issues), I think the on-line grader will become the de-facto standard for contest writers, due to the feedback it provides. We will still allow teachers and students to choose to grade off-line, but the selection of languages (C, C++, Pascal, Java, Python, Perl and PHP) will hopefully cover the vast majority of competitors. Again, if students want to learn Python, check out the CS Cirlces On-line Resource at: cscircles.cemc.uwaterloo.ca We continued the collaboration with Tsinghua University in Beijing and the University of Hong Kong to offer the contest to Beijing and Hong Kong high school students. More information (including results) can be found at: http://ccc.cs.tsinghua.edu.cn/ and http://www.cs.hku.hk/ccc2013/. As in previous years, the organizers from Tsinghua and HKU collaborated with UW to create a contest different than the Canadian CCC. Below, a qualitative summary of both the Junior and Senior contest is presented. -

2009 Results Sun Life Financial Canadian Open Mathematics
in collaboration with / en collaboration avec The CENTRE for EDUCATION Le CENTRE d'EDUCATION´ in MATHEMATICS en MATHEMATIQUES´ and COMPUTING et en INFORMATIQUE Faculty of Mathematics Facult´ede math´ematiques University of Waterloo Universit´ede Waterloo Waterloo, Ontario, Canada N2L 3G1 Waterloo, Ontario, Canada N2L 3G1 2009 2009 Results R´esultats Sun Life Financial D´efiouvert Canadian Open canadien Mathematics de math´ematiques Challenge Financi`ere Sun Life 2009 Canadian Mathematical Society © 2009 La Soci´et´emath´ematiquedu Canada Introduction Introduction The Sun Life Financial Canadian Open Mathematics Challenge (COMC) is a collaborative initiative between the Canadian Mathematical Society (CMS) and Centre for Education in Mathematics and Computing (CEMC), based at the University of Waterloo. The competition is one in a series of CMS competitions leading to the selection of the Canadian student team to compete in the International Mathematical Olympiad (IMO), and provides an excellent complement to the CEMC's mathematical competitions. The purpose of the Sun Life Financial COMC is to encourage students to explore, discover, and learn more about mathematics and problem solving. At the same time, the competition serves to provide teachers with a unique student enrichment activity during the fall term. Outstanding performance in the Sun Life Financial COMC is recognized in three ways. First, Provincial Cham- pions and their respective schools are each awarded a plaque. Second, a number of high-ranking students in each jurisdiction are awarded Gold Medals. Third, the top-ranked fifty or so students are invited to write the more advanced Canadian Mathematical Olympiad (CMO), and their schools each receive a subscription to the CMS's internationally recognized problem solving journal CRUX with MAYHEM. -

2011 Results Pascal Contest Cayley Contest Fermat Contest 2011 Résultats Concours Pascal Concours Cayley Concours Fermat
The CENTRE for EDUCATION in MATHEMATICS and COMPUTING Le CENTRE d'EDUCATION´ en MATHEMATIQUES´ et en INFORMATIQUE www.cemc.uwaterloo.ca 2011 2011 Results R´esultats Pascal Contest Concours Pascal (Grade 9) (9e ann´ee{ Sec. III) Cayley Contest Concours Cayley (Grade 10) (10e ann´ee{ Sec. IV) Fermat Contest Concours Fermat (Grade 11) (11e ann´ee{ Sec. V) c 2011 Centre for Education in Mathematics and Computing Competition Organization Organisation du Concours Centre for Education in Mathematics and Computing Faculty and Staff / Personnel du Concours canadien de math´ematiques Ed Anderson Lloyd Auckland Terry Bae Steve Brown Ersal Cahit Karen Cole Jennifer Couture Serge D'Alessio Frank DeMaio Fiona Dunbar Mike Eden Barry Ferguson Barb Forrest Judy Fox Steve Furino John Galbraith Sandy Graham Angie Hildebrand Judith Koeller Joanne Kursikowski Bev Marshman Dean Murray Jen Nissen J.P. Pretti Linda Schmidt Kim Schnarr Jim Schurter Carolyn Sedore Ian VanderBurgh Troy Vasiga 2 Competition Organization Organisation du Concours Problems Committees / Comit´esdes probl`emes Pascal Contest / Concours Pascal Wally Webster (Chair / pr´esident), Dashwood, ON Lloyd Auckland, St. Thomas, ON Janet Christ, Walter Murray C.I., Saskatoon, SK J.P. Pretti, University of Waterloo, Waterloo, ON Jim Schurter, University of Waterloo, Waterloo, ON Tyler Somer, Kitchener, ON Anna Spanik, Halifax West H.S., Halifax, NS Aaron Warner, St. Mildred's-Lightbourn School, Oakville, ON Cayley Contest / Concours Cayley Jen Nissen (Chair / pr´esidente), University of Waterloo,