Flood Forecast Systems 1 Introduction
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Rapid Attribution of Heavy Rainfall Events Leading to the Severe Flooding in Western Europe During July 2021
Rapid attribution of heavy rainfall events leading to the severe flooding in Western Europe during July 2021 Contributors Frank Kreienkamp1, Sjoukje Y. Philip2, Jordis S. Tradowsky1,4, Sarah F. Kew2, Philip Lorenz1, Julie Arrighi7,8,9, Alexandre Belleflamme16, Thomas Bettmann18, Steven Caluwaerts13,19, Steven C. Chan14, Andrew Ciavarella22, Lesley De Cruz13, Hylke de Vries2, Norbert Demuth18, Andrew Ferrone17, Erich M. Fischer6, Hayley J. Fowler14, Klaus Goergen16, Dorothy Heinrich7, Yvonne Henrichs18, Geert Lenderink2, Frank Kaspar10, Enno Nilson15, Friederike E L Otto11, Francesco Ragone13,20, Sonia I. Seneviratne6, Roop K. Singh7, Amalie Skålevåg, Piet Termonia13,19, Lisa Thalheimer11, Maarten van Aalst7,8,21, Joris Van den Bergh13, Hans Van de Vyver13, Stéphane Vannitsem13, Geert Jan van Oldenborgh2,3, Bert Van Schaeybroeck13, Robert Vautard5, Demi Vonk8, Niko Wanders12 1 - Deutscher Wetterdienst (DWD), Regionales Klimabüro Potsdam, Potsdam, Germany; 2 - Royal Netherlands Meteorological Institute (KNMI), De Bilt, The Netherlands; 3 - Atmospheric, Oceanic and Planetary Physics, University of Oxford, UK; 4 - Bodeker Scientific, Alexandra, New Zealand; 5 - Institut Pierre-Simon Laplace, CNRS, Paris, France; 6 - Institute for Atmospheric and Climate Science, Department of Environmental Systems Science, ETH Zurich, Zurich, Switzerland; 7 - Red Cross Red Crescent Climate Centre, The Hague, the Netherlands; 8 - Faculty of Geo-Information Science and Earth Observation (ITC), University of Twente, Enschede, the Netherlands; 9 - Global Disaster -

The Attack Will Go on the 317Th Infantry Regiment in World War Ii
Louisiana State University LSU Digital Commons LSU Master's Theses Graduate School 2003 The tta ack will go on the 317th Infantry Regiment in World War II Dean James Dominique Louisiana State University and Agricultural and Mechanical College, [email protected] Follow this and additional works at: https://digitalcommons.lsu.edu/gradschool_theses Part of the Arts and Humanities Commons Recommended Citation Dominique, Dean James, "The tta ack will go on the 317th Infantry Regiment in World War II" (2003). LSU Master's Theses. 3946. https://digitalcommons.lsu.edu/gradschool_theses/3946 This Thesis is brought to you for free and open access by the Graduate School at LSU Digital Commons. It has been accepted for inclusion in LSU Master's Theses by an authorized graduate school editor of LSU Digital Commons. For more information, please contact [email protected]. THE ATTACK WILL GO ON THE 317TH INFANTRY REGIMENT IN WORLD WAR II A Thesis Submitted to the Graduate Faculty of the Louisiana State University and Agricultural and Mechanical College in partial fulfillment of the requirements for a degree of Master of Arts in Liberal Arts In The Interdepartmental Program in Liberal Arts by Dean James Dominique B.S., Regis University, 1997 August 2003 i ii TABLE OF CONTENTS LIST OF MAPS........................................................................................................... iii ABSTRACT................................................................................................................. iv INTRODUCTION .........................................................................................................1 -

Council CNL(14)23 Annual Progress Report on Actions Taken
Agenda Item 6.1 For Information Council CNL(14)23 Annual Progress Report on Actions Taken Under Implementation Plans for the Calendar Year 2013 EU – Germany CNL(14)23 Annual Progress Report on Actions taken under Implementation Plans for the Calendar Year 2013 The primary purposes of the Annual Progress Reports are to provide details of: • any changes to the management regime for salmon and consequent changes to the Implementation Plan; • actions that have been taken under the Implementation Plan in the previous year; • significant changes to the status of stocks, and a report on catches; and • actions taken in accordance with the provisions of the Convention These reports will be reviewed by the Council. Please complete this form and return it to the Secretariat by 1 April 2014. The annual report 2013 is structured according to the catchments of the rivers Rhine, Ems, Weser and Elbe. Party: European Union Jurisdiction/Region: Germany 1: Changes to the Implementation Plan 1.1 Describe any proposed revisions to the Implementation Plan and, where appropriate, provide a revised plan. Item 3.3 - Provide an update on progress against actions relating to Aquaculture, Introductions and Transfers and Transgenics (section 4.8 of the Implementation Plan) - has been supplemented by a new measure (A2). 1.2 Describe any major new initiatives or achievements for salmon conservation and management that you wish to highlight. Rhine ICPR The 15th Conference of Rhine Ministers held on 28th October 2013 in Basel has agreed on the following points for the rebuilding of a self-sustainable salmon population in the Rhine system in its Communiqué of Ministers (www.iksr.org / International Cooperation / Conferences of Ministers): - Salmon stocking can be reduced step by step in parts of the River Sieg system in the lower reaches of the Rhine, even though such stocking measures on the long run remain absolutely essential in the upper reaches of the Rhine, in order to increase the number of returnees and to enhance the carefully starting natural reproduction. -
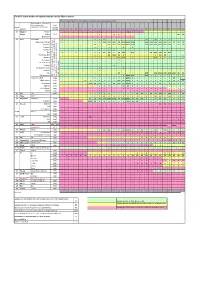
Proof of Reproduction of Salmon Returned to the Rhine System
Proof of reproduction of salmon returned to the Rhine system Year of spawning proof (reproduction during the preceding autumn/winter) Project water - Selection of the most important First Countr tributaries (* no stocking) salmon y System stocking 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016 2017 2018 2019 2020 D Wupper- Wupper / / / / / / / / 0 / / / / / (X) / / / / / / / / / / X Dhünn Dhünn 1993 / / / / / / / / 0 / / X X / / / / / / / / / / / XX XX Eifgenbach / / / / / / / / / / / / 0 / / / / / / / / / / / / / D Sieg Sieg NRW X / / / / / / X 0 XX / / / / / / / / XX / XX 0 0 0 / / / Agger (lower 30 km) X / / / / / / 0 0 XXX XXX XXX XX XXXX XXXX XXXX / / XXX XXX XXX XXX XXX XX XX XX XX Naafbach / / / / / / / XX 0 / XXX XXX XXX XXXX XXXX XXXX / / XXX XXX XXX XXXX XXX XXX 0 XX XX Pleisbach / / / / / / / 0 / / 0 / / X / X / / / / / / / / / / Hanfbach / / / / / / / / 0 / 0 X / / / / / / / / / / / / / / Bröl X / / X / / / 0 0 XX XX 0 XX XXX / XXX / / / XX XXX XXX XX XXX / / Homburger Bröl / / / / / / / 0 0 / XX XXX XX X / / / / / / 0 XX XX 0 / / 0 Waldbröl / / / / / / / 0 0 / 0 0 XXX XXX / 0 / / / / XXX 0 0 0 / / 0 Derenbach / / / / / / / / / / / / 0 / / / / / / / / / / / / / Steinchesbach / / / / / / / / / / / / 0 / / / / / / / / / / / / / Krabach / / / / / / / / / / / X / / / / / / / / / / / / / / Gierzhagener Bach / / / / / / / / 0 / / / / X / / / / / / / / / / / / Irsenbach / / / / / / / / 0 / / / / / / / / / / / / / / / / / Sülz / / / / / / / 0 0 / / / XX / / / / / -

Anhang 1 Wasserkörper Im BG Mosel-Saar (Oberflächen- Und Grundwasserkörper)
Maßnahmenprogramm BG Mosel-Saar – Anhang 1 Anhang 1 Wasserkörper im BG Mosel-Saar (Oberflächen- und Grundwasserkörper) Tabelle 1.1: Darstellung der Oberflächenwasserkörper im BG Mosel-Saar, in denen eine Veränderung der Bewertung im Vergleich zu 2009 erfolgte und für die eine Ursache der Veränderung genannt wurde Ökologischer Ökologischer Ökologischer Ursache Wasserkörpername HMWB Zustand 2009 Zustand 2015 Zustand 2020 Veränderung Alf-Sammetbach NWB 2 2 3 2 Altlayer Bach NWB 2 2 3 3 Baybach NWB 2 2 3 3 Bickenalb NWB 3 4 3 9 Bieberbach NWB neu 4 5 3 Biewerbach NWB 4 3 2 1 Dünnbach NWB 2 2 3 6 Ehlenzbach NWB 2 3 2 6 Fellerbach NWB 3 2 3 6 Föhrenbach NWB 3 3 4 2 Glaadtbach NWB 4 4 2 9 Großbach (Mosel) NWB 2 2 3 3 Konzer Bach HMWB 5 5 4 3 Lambach NWB 5 3 2 3 Lambsbach NWB 3 5 4 9 Lammbach NWB 3 4 5 6 Lützbach NWB 2 2 3 6 Mittlere Nims NWB 2 4 3 6 Nothbach NWB 5 4 5 3 Obere Salm NWB 1 2 3 3 Oberer Elzbach NWB 3 2 3 3 Oberer Kautenbach NWB neu 1 2 3 Oberer Spanger Bach NWB 4 5 4 6 Oosbach NWB 2 3 2 6 Rommelsbach NWB 5 5 4 6 Schönbach NWB 2 5 2 1 Selchenbach NWB 2 3 4 9 Stillegraben NWB 2 1 2 6 Taubkyll NWB 2 2 3 3 Trualbe HMWB 4 4 3 1 Untere Alf NWB 3 2 3 2 Untere Dhron NWB 2 2 3 3 Untere Enz NWB 2 2 3 3 Untere Irsen NWB 2 2 3 6 Untere Kleine Dhron NWB 4 3 4 6 Untere Lieser NWB 3 3 4 6 Maßnahmenprogramm BG Mosel-Saar – Anhang 1 Ökologischer Ökologischer Ökologischer Ursache Wasserkörpername HMWB Zustand 2009 Zustand 2015 Zustand 2020 Veränderung Untere Mosel HMWB 5 4 5 6 Untere Rodalb HMWB 3 2 3 3 Untere Ruwer NWB 2 2 3 3 Unterer Kautenbach NWB 4 4 5 6 Unterer Ueßbach NWB 2 2 3 3 Veldenzbach NWB 4 2 3 3 Vlierbach NWB 3 4 3 3 Waldholzbach NWB 2 4 3 9 Wallhalbe NWB 3 4 3 1 Weilerbach NWB 2 1 2 6 Welschbilligerbach NWB 4 4 2 2 Wiltinger Bogen NWB 5 4 5 6 Wirft NWB 2 2 4 6 (1) Veränderung aufgrund durchgeführter Maßnahmen (2) Veränderung aufgrund veränderter Belastungen (3) Veränderung aufgrund eines grundsätzlich veränderten Vorgehens beim Monitoring und/oder Zustandsbewertung (inkl. -

HOLIDAY PLANNER Hosts and Travel Offers
VISIT TRIER ENGLISH HOLIDAY PLANNER Hosts and Travel Offers 2021 www.trier-info.de Map showing Trier hotels … this sign points the way Pictograms of the hotels Classifi cations Pictograms of the apartments A1 Hotels 5 10 grid square/Hotel-No. non-smoking-room number of persons barrier-free Nr. 13 ★★★★★ = Luxury ★★★★ = First Class ★★★ = Comfort TRAVEL REQUEST FORM 250 Room for meetings/ number of beds ★★ = Standard 60 festivities ★ = Tourist square metre bed linen included S = This provider has signifi cantly more For your personalized offer please contact us and tell us your wishes: Trier Tourismus und Marketing GmbH/ 15 classifi cation points than is required restaurant inside Pets allowed for its classifi cation. Hotel department, Simeonstr. 55, 54290 Trier, Fax +49 (0) 651 / 978 08-69, Tel. +49 (0) 651 / 978 08-16 (-14) kitchen towels included Holiday rooms, Vacation/holiday bath/toilet fond of children apartments Lawn/garden for = First-class furnishings bath/toilet sunbathing = High-quality overall furnishings Travel Offer shower/toilet Motorcycle-friendly = Good, cozy furnishings = Medium comfort = Simple, purposeful furnishings shower/toilet terrace hair dryer Bicycle-friendly 54 Guest-houses, inns, and boarding houses phone solarium television playground Arrival day Departure day G★★★★★ = Accom. with the highest standards G★★★★ = Accom. with high standards 21 G★★★ = Accom. with elevated standards 23 30 G★★ = Accom. with medium standards � WiFi in the room sauna radio barbecue Please inform me about the following additional services: G★ = Accom. with simple standards 37 television massage Providers without stars have not participated in the voluntary classifi cation. An evaluation of WiFi balcony the provider ist the therefore not bound to a � classifi cation. -

COMMISSION DECISION of 20 March 2009 Amending Decision 2003/135
L 75/24EN Official Journal of the European Union 21.3.2009 COMMISSION DECISION of 20 March 2009 amending Decision 2003/135/EC as regards the eradication and emergency vaccination plans for classical swine fever in feral pigs in certain areas of the Federal States of North Rhine-Westphalia and Rhineland-Palatinate (Germany) (notified under document number C(2009) 1669) (Only the French and German texts are authentic) (2009/255/EC) THE COMMISSION OF THE EUROPEAN COMMUNITIES, phalia and Rhineland-Palatinate which was free of the disease so far have been reported. Accordingly, the eradi Having regard to the Treaty establishing the European cation and emergency vaccination plans for classical Community, swine fever in feral pigs needs to be applied in those areas. Having regard to Council Directive 2001/89/EC of 23 October 2001 on Community measures for the control of classical swine (5) Decision 2003/135/EC should therefore be amended fever (1), and in particular Article 16(1) and 20(2) thereof, accordingly. Whereas: (6) The measures provided for in this Decision are in accordance with the opinion of the Standing (1) Commission Decision 2003/135/EC of 27 February Committee on the Food Chain and Animal Health, 2003 on the approval of the plans for the eradication of classical swine fever and the emergency vaccination of HAS ADOPTED THIS DECISION: feral pigs against classical swine fever in Germany, in the Federal States of Lower Saxony, North Rhine-Westphalia, Article 1 Rhineland-Palatinate and Saarland (2) was adopted as one of a number of measures to combat classical swine fever. -

To Discover and Enjoy the Mosel Region
Discover and enjoy the Moselle countryside 2 At the top A warm welcome to the Moselle, Saar und Ruwer ... a countryside of superlatives awaiting your visit! It is here that winegrowers produce top international wines, it is here that the Romans founded the oldest city of Germany, it is here that you will find one of the most successful combinations of rich, ancient culture and countryside, which is sometimes gentle and sometimes spectacular. As far as the art of living is concerned, the proximity to France and Luxem- bourg inspires not only the cuisine of the Moselle region. There is hardly any other holiday region that has so many fascinating facets. 3 Winegrowers who cultivate steep hillsi INSIDE GERMANY the Moselle care and manual work. A winegro- has cut its way through deep wer must not suffer from vertigo gorges and countless meanders here! The steep slopes and terraces, into the mountains over a distance with their mild micro-climate and of more than 240 kilometres, until slate ground that stores the heat, it meets Father Rhine in Koblenz. are the ideal conditions for the Europe’s steepest vineyard, the Riesling grape, which produces the Bremmer Calmont, with a 68° uniquely delicate fruity and tangy slope, is situated in the largest wines along the Moselle, Saar and enclosed area of cliffs in the world: Ruwer. The dry Moselle wines, in roughly half of the Moselle vine- particular, that are cultivated by the yards, comprising around 10,000 5000 or so winegrowers, with a hectares in total, are cultivated in wealth of individual nuances, are 4 this way, which demands a lot of an excellent accompaniment to ides are heroes delicate dishes. -

Air Power for Patton's Army
AIR POWER FOR PATTON’S ARMY The XIX Tactical Air Command in the Second World War David N. Spires Air Force History and Museums Program Washington, D. C. 2002 Library of Congress Cataloging-in-Publication Data Spires, David N. Air Power for Patton’s Army : the XIX Tactical Air Command in the Second World War / David N. Spires. p. cm. Includes bibliographical references and index. 1. World War, 1939-1945—Aerial operations, American. 2. United States. Army Air Forces. Tactical Air Command, 19th—History. 3. World War, 1939- 1945—Campaigns—Western Front. 4. Close air sup- port—History—20th century. 5. United States. Army. Army, 3rd—History. I. Title. D790 .S65 2002 940.54’4973—dc21 2002000903 In Memory of Colonel John F. “Fred” Shiner, USAF (1942–1995) Foreword This insightful work by David N. Spires holds many lessons in tacti- cal air-ground operations. Despite peacetime rivalries in the drafting of service doctrine, in World War II the immense pressures of wartime drove army and air commanders to cooperate in the effective prosecution of battlefield opera- tions. In northwest Europe during the war, the combination of the U.S. Third Army commanded by Lt. Gen. George S. Patton and the XIX Tactical Air Command led by Brig. Gen. Otto P. Weyland proved to be the most effective allied air-ground team of World War II. The great success of Patton’s drive across France, ultimately crossing the Rhine, and then racing across southern Germany, owed a great deal to Weyland’s airmen of the XIX Tactical Air Command. This deft cooperation paved the way for allied victory in Westren Europe and today remains a clas- sic example of air-ground effectiveness. -

Tank Busters
TANK BUSTERS THE HISTORY of the 607thTANK DESTROYER BATTALION IN COMBAT ON THE WESTERN FRONT Printed in Munich of Bavaria by Knorr & Hirth, Sendlinger Strasse 83 DEDICATED TO THE SOLDIERS WHO DIED SO THAT OTHERS MIGHT BE FREE TO LIVE AS THEY DESIRE. BATTALION HISTORY STAFF 1st Lt. HAROLD H. EBY, Historian T/Sgt. ORNO D. STRONG JR., Layout T/5 FRANK W. DAVIS, Artist T/5 ROY M. KEMP, Typist Acknowledgment is made to the officers of all companies who aided in submitting stories from their units and to all the men who submitted the pictures found in this book. CONTENTS FRONT MATTER Section 01 FOREWORD INTRODUCTION PART ONE NORMANDY AND FALAISE BATTLES Section 02 The Buildup The Breakthrough On To Le Mans Closing The Trap MOSELLE RIVER AND METZ BATTLES Section 03 Racing Through France Fighting For The Moselle Storming Of Metz THE SIEGFRIED BATTLES Section 04 Racing For The Saar The Bridgehead The Defensive Against The Siegfried Again RHINE BATTLES Section05 The Approach The Crossing First Task Force Second Task Force PART TWO COMMENDATIONS & BATTALION ROSTERS Section 06 LT. COL. HARALD S. SUNDT FOREWORD SOLDIERS of the 607th Tank Destroyer Battalion: This memento of our labor and sacrifice, of our teamwork and cooperation with the combined arms of our Army will take on increasing importance in our lives as the stress of battle grows dim and the struggle for a better world, socially, economically, politically, and religiously goes on. In the carrying out of your assigned missions there will be trials, there will be triumphs, there will be disasters, for you individually or as a member of the group with whom you may be associated. -

WELCOME to Our Region!
WELCOME T O O UR R E GI O N! H O S T N A T I O N C O U nc I L S PA N GDA H L E M E .V. 2 GERMAN-AMERICAN We would like to consider this wonderful German- American relationship as indispensable for both na- FRIENDSHIP – A STRONG tions. ALLIANCE And when Spangdahlem Air Base celebrated its 50th anniversary in 2003 German political, economical and HOST NATION COUncIL – AN INITIATIVE social representatives took advantage of this opportu- FOR US CITIZENS IN THE REGION nity and realized a long cherished desire: Foundation of the Host Nation Council. In 1953 this region gained a very important institution: With this foundation, the Host Nation Council wanted Spangdahlem Air Base! to enhance the already existing strong support for all What an enormous new experience for the people in American neighbours, underline the importance of the the Eifel! local US Forces presence and stress the significant meaning of our friendship. We are striving for the Eifel Although, first rather cautious, people in the Eifel to become your ’Home away from Home‘. And last, soon developed a certain curiosity towards these but not least, the Council's foundation is to serve as a new neighbours coming from an entirely different sign of gratitude for over 50 years of liberty, freedom part of the world. Soon their culture, their customs and democracy, guaranteed by the US leadership and and courtesies were very much appreciated and had its service members. more and more a formative influence on the life of the Eifel citizens thus presenting a mutual enrichment for The Council's chairman and head of the Board is both nations, which again resulted in a unique and Jan Niewodniczanski with Michael Billen harmonious living together. -

Master Plan Migratory Fish Rhine
Master Plan Migratory Fish Rhine Report No. 179 Imprint Publisher: International Commission for the Protection of the Rhine (ICPR) Kaiserin-Augusta-Anlagen 15, D 56068 Koblenz P.O. box 20 02 53, D 56002 Koblenz Telephone +49-(0)261-94252-0, Fax +49-(0)261-94252-52 Email: [email protected] www.iksr.org ISBN 978-3-941994-09-6 © IKSR-CIPR-ICBR 2009 Report 179e.doc Internationale Kommission zum Schutz des Rheins International Commission for the Protection of the Rhine Commission Internationale pour la Protection du Rhin Internationale Commissie ter Bescherming van de Rijn Master Plan Migratory Fish Rhine ICPR report no. 179 1. Initial conditions ..................................................................................... 2 2. Background............................................................................................ 3 3. Already implemented measures for anadromous migratory fish...................... 5 4. Measures planned for anadromous migratory fish in the different sections of the Rhine.................................................................................................... 6 4.1 River Continuity and Habitats...................................................................... 6 4.1.1 Delta Rhine............................................................................................ 6 4.1.2 Lower Rhine........................................................................................... 7 4.1.3 Middle Rhine .........................................................................................