DOCSLIB.ORG

Determination of a Reaction's Activated Energy Using Naoh As A

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Determination of a Reaction's Activated Energy Using Naoh As A DOI: 10.26717/BJSTR.2018.06.001282 Anita Kovač Kralj. Biomed J Sci & Tech Res ISSN: 2574-1241 Research Article Open Access Determination of a Reaction’s Activated Energy Using Naoh as a Reactant Anita Kovač Kralj* Faculty of Chemistry and Chemical Engineering, University of Maribor, Slovenia Received: June 14, 2018; Published: June 21, 2018 *Corresponding author: Anita Kovač Kralj, Faculty of Chemistry and Chemical Engineering, University of Maribor, Smetanova 17, Maribor, Slovenia Abstract Determining chemical kinetics is the basis for reactor design, the determining of activated energy, energy efficiency, steam production, and integrating the reactor’s outlet stream with the inlet. The purpose of this article is to describe a sensitivity method for concentration and activated energy determination. This sensitivity method defines the sensitivity parameter for determining the characteristics of a reaction using strong electrolytes (for example sodium hydroxide - NaOH) as reactants. The sensitivity parameter is constant throughout this specific reaction. Concentrations of strong electrolytes can be determined by the sensitivity method, which is based on the measurement of conductivities. This method proposes continuous concentration determination of NaOH (or strong electrolyte) as a reactant or product. This sensitivity method wasKeywords: tested using titration. Sensitivity Method; Strong Electrolyte; Concentration; Activation Energy Introduction algorithms. Advances in computing have allowed researchers to The basis is presented for determining concentration and obtain increasing amounts of chemically-relevant information activated energies from the reactions of strong electrolytes. from their data; however, this is not always achieved using simple Determining these concentrations is basic for analytical chemistry, data-processing techniques. It is important to establish true using different methods. Eldridge, Piret [1] obtained the pseudo- mathematical models for utilization within the chemical industry first-order reaction rate constant using a batch reactor. In order [4]. to determine the acetic anhydride concentration, samples from the reactor were withdrawn into tarred flasks containing 15-20 Chemical kinetics, also known as reaction kinetics, is the times the quantity of saturated aniline-water required to react study of chemical processes’ rates. Chemical kinetics includes with the sample. Since the anhydride rapidly acetylates the aniline, investigations into how different experimental conditions can thus producing acetanilide and acetic acid, the samples were then influence the speed of a chemical reaction and yield information titrated to determine the concentration of acetic acid. In another about the reaction’s mechanism and transition states, as well as study, Shatyski and Hanesian [2] determined the kinetics of the the construction of mathematical models that can describe the above reaction by using temperature-time data obtained under characteristics of a chemical reaction. In 1864, Peter Waage and adiabatic conditions within a batch reactor. The use of in-situ FTIR Cato Guldberg pioneered the development of chemical kinetics by spectroscopy has already been demonstrated, when following the formulating the law of mass action, which states that the speed of hydrolysis of acetic anhydride reaction [3]. An analysis of the batch a chemical reaction is proportional to the quantity of the reacting reactor’s data showed that the hydrolysis of acetic anhydride is a substances [5]. The different forms of energy include kinetic, pseudo-first order reaction. The rate constants were calculated potential, thermal, gravitational, sound, elastic, and electromagnetic from the batch data using both integral and differential methods energy. These forms of energy are often named after a related force. of analysis. German physicist Hermann von Helmholtz established that all A forms of energy are equivalent-energy in one form can disappear Advances in electronics and computing over the past 30 but the same amount of energy will reappear in another form. years have revolutionized the analytical laboratory. Technological restatement of this idea is that energy is subject to a conservation developments have allowed instruments to become smaller, law over time [6]. This paper studies the concentration and activated faster, and cheaper, while continuing to increase accuracy, energy determined by the reactant NaOH (strong electrolytes), precision, and availability. Furthermore, software sold with many using the sensitivity method. commercial instruments contains automatic data-processing Cite this article: : . 4937 Anita Kovač Kralj. Determination of a Reaction’s Activated Energy Using Naoh as a Reactant. Biomed J Sci&Tech Res 6(1)- 2018. BJSTR. MS.ID.001282. DOI 10.26717/ BJSTR.2018.06.001282 Anita Kovač Kralj. Biomed J Sci & Tech Res Volume 6- Issue 1: 2018 The Sensitivity Method Λ = Λo − m m K c Λm (2.5) The sensitivity method is an alternative method for accurately 2 Where introduces the molar conductivity in Siemens metre- quantifying reactant or product concentrations during NaOH (strong −1 κ Λ = electrolytes) determination. This method applies a sensitivity squared per mole (S m molm ), which is defined as: c parameter for determining concentrations and activated energies c (2.6) for strong electrolytes (such as NaOH), by using conductivity. κ Specific characteristic-sensitivity parameter (s) can be found from Where is the molar concentration of the added−1 electrolyte, Λo c and is the conductivitym in siemens per metre (S m ). the measurements for strong electrolytes. Concentrations of strong o t) Λ electrolytes ( can be determined by using the sensitivity method. The constant is the limiting molar conductivity, the molarm This method proposes a continuous determination of reactant or s conductivity within the limit of zero concentration. The for product concentrations. Each reaction using NaOH as reactant has sodium o hydroxide at a temperature2 of around 25°C is2 [7]: Λ=m 5.01 + 19.91 = 24.92 the specific characteristic sensitivity parameter ( ), which can be −1 −1 mS m mol = 2492 mS dm mol (2.7) determined using the sensitivity method by applying conductivity. c κ0 Conductivity for a specific reaction has a specific characteristic, Kohlrausch’s constant can0 be calculated by known values for therefore certain sensitivity parameters can be determined -the the initial concentration ( ) and initial conductivity ( ), using sensitivity constant, which is constant during a specific reaction. equations 2.5 and 2.6: Λo κ K = m − 0 c 0.5 c 1.5 0 0 (2.8) The essence of the strong electrolytes theory is that you can determine the concentration of a reactant or product. The reaction can be observed by using the concentrationκ calculation. The two Λo − K c = basic equations 2.5 and 2.6m are used:c (2.9) The concentration is expressed by equation 2.9 for the numerical method: κ + c1.5K c = o Λm (2.10) Figure 1: The sensitivity method. The concentration can be calculated by using a numerical method (eq. 2.10; for example successive substitution; addition A). This sensitivity method is a very simple method for the The initial concentration (zc) and the allowed differences between determining concentrations cc=–· ∆ ofκ strong s electrolytes (Figure 1): t 00 the initial and target values (EPS) are needed. The determination of (2.1) cct =00–· ∆κ s any concentration change by using a numerical method is very long- cc= – (κκ–) · s (2.2) term, so it is only used at the beginning so that you can determine tt00 the sensitivity constant of the conductivity. The sensitivity method (2.3) was tested for various real reactions by using NaOH as reactant c t Case(chapter study 3) (Figure 1). The non-reactive reactant’s (such as NaOH),κ concentration depends on time ( ) which can be calculated by using equations 2.1 or 2.3 with a difference in conductivitys (Δ ; eq. 2.2). The sensitivity method was tested to synthesize sodium The sensitivity constant ( ) for a specific reaction can be methoxide, sodium benzoate, and sodium acetate. Sodium calculated by equations= ( cc2.4:00 − tt) /–(κκ) hydroxide (NaOH) was, in all cases, the reactant and a strong Sodium Methoxide Synthesis κ electrolyte. c0 0 (2.4) is the known initial reactant’s concentration and is the 3 known initial conductivity of strong electrolytest (NaOH). We need Sodium methoxide (CH ONa) was produced from sodium c only a fewt measurements of conductivity κ , depending on time, hydroxideNaOH (NaOH) + CH and OH methanol = H O ++ Na(MeOH)+− CH in O a batch reactor: s 32 3 so that can be calculated using the Kohlrausch law (equations (R1) 2.5; [7]). The constant is equal for all measurements. Friedrich Kohlrausch showed that, at low concentrations, the molar A B C conductivities of strong electrolytes vary linearly with the square The main application of sodium methoxide today is its use root of the concentration: as a catalyst in the production of bio-diesel. During this process, Biomedical Journal of Scientific & Technical Research (BJSTR) 4938 Anita Kovač Kralj. Biomed J Sci & Tech Res Volume 6- Issue 1: 2018 Table 1: Experimental data and calculation for sodium methoxide synthesis, using numerical and sensitivity methods. vegetable oils or animal fats, which are chemically fatty acid triglycerides, are transesterified with methanol to produce fatty cA /(mol/L) cA /(mol/L) acida) methyl Determining esters (FAMEs). the concentration using the sensitivity t/min κ/(mS/dm) calculated by calculated by num. meth. sens. meth. method: 0.00 A schematic diagram of the laboratory apparatus is 0.80 247.0240.0 0.1670 shown in (Figure 2). A batch reactor with a stirrer was used in 0.91 0.1599 0.1599 the experiment. Methanol (0.12mL) was heated into a reactor at a temperature of 28 °C, and 3.34g pure NaOH was dissolved 238.0 0.1578 κt t 2.00 in 500mL of water. Both substances were mixed and the 1.25 236.7 0.1565 0.1565 κ0 conductivity ( ) was measured depending on time, (Table 234.1 0.1539 cA0, 1). The first conductivity of the sodium hydroxide ( ) was 2.25 233.5 0.1532 0.1532 247mS/dm.
Load more

Recommended publications
  • Methanogenesis Rates in Acetate and Nitrate Amended Anoxic Slurries
    Methanogenesis rates in acetate and nitrate amended anoxic slurries BIOS 35502: Practicum in Environmental Field Biology Patrick Revord Advisor: William West 2011 Abstract With increasing urbanization and land use changes, pollution of lakes and wetland ecosystems is imminent. Any influx of nutrients, anthropogenic or natural, can have dramatic effects on lake gas production and flux. However, the net effect of simultaneous increase of both acetate and nitrate is unknown. Methane (CH4) production was measured in anoxic sediment and water slurries amended with ammonium nitrate (NH4NO3), which has been shown to inhibit methanogenesis, and sodium acetate (CH3COONa or NaOAc), which is known to increase methanogenesis. The addition of acetate significantly increased the methanogenesis rate, but the nitrate amendment had no significant effect. The simultaneous amendment of both acetate and nitrate showed no significant increase in CH4 compared to the control, indicating that the presence of nitrate may have reduced the effect of acetate amendment. Introduction Methane, a greenhouse gas associated with global warming, continues to increase in concentration in our atmosphere. Global yearly flux of methane into the atmosphere is 566 teragrams of CH4 per year, which is more than double pre-industrial yearly flux (Solomon et al. 2007). Increasing urbanization and land-use changes contribute significantly to increased gas levels (Anderson et al. 2010, Vitousek 1994). Nutrients travel from anthropogenic sources such as wastewater treatment facilities, landfills, and agricultural plots into nearby lakes, rivers, and wetlands, causing increased primary productivity in a process known as eutrophication (Vitousek et al. 1997). The increased nutrients and productivity lead to toxic algal blooms that create products such as acetate, H2, and CO2; a nutrient-rich anoxic environment suitable for anaerobic bacteria to produce unnaturally high levels of methane and other greenhouse gases (Davis and Koop 2006, West unpublished data).
    [Show full text]
  • NMR Chemical Shifts of Common Laboratory Solvents As Trace Impurities
    7512 J. Org. Chem. 1997, 62, 7512-7515 NMR Chemical Shifts of Common Laboratory Solvents as Trace Impurities Hugo E. Gottlieb,* Vadim Kotlyar, and Abraham Nudelman* Department of Chemistry, Bar-Ilan University, Ramat-Gan 52900, Israel Received June 27, 1997 In the course of the routine use of NMR as an aid for organic chemistry, a day-to-day problem is the identifica- tion of signals deriving from common contaminants (water, solvents, stabilizers, oils) in less-than-analyti- cally-pure samples. This data may be available in the literature, but the time involved in searching for it may be considerable. Another issue is the concentration dependence of chemical shifts (especially 1H); results obtained two or three decades ago usually refer to much Figure 1. Chemical shift of HDO as a function of tempera- more concentrated samples, and run at lower magnetic ture. fields, than today’s practice. 1 13 We therefore decided to collect H and C chemical dependent (vide infra). Also, any potential hydrogen- shifts of what are, in our experience, the most popular bond acceptor will tend to shift the water signal down- “extra peaks” in a variety of commonly used NMR field; this is particularly true for nonpolar solvents. In solvents, in the hope that this will be of assistance to contrast, in e.g. DMSO the water is already strongly the practicing chemist. hydrogen-bonded to the solvent, and solutes have only a negligible effect on its chemical shift. This is also true Experimental Section for D2O; the chemical shift of the residual HDO is very NMR spectra were taken in a Bruker DPX-300 instrument temperature-dependent (vide infra) but, maybe counter- (300.1 and 75.5 MHz for 1H and 13C, respectively).
    [Show full text]
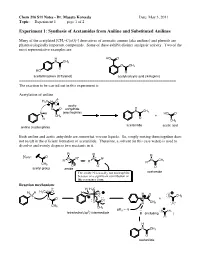
  • Experiment 1: Synthesis of Acetamides from Aniline and Substituted Anilines
    Chem 216 S11 Notes - Dr. Masato Koreeda Date: May 3, 2011 Topic: __Experiment 1____ page 1 of 2. Experiment 1: Synthesis of Acetamides from Aniline and Substituted Anilines Many of the acetylated [CH3–C(=O)-] derivatives of aromatic amines (aka anilines) and phenols are pharmacologically important compounds. Some of these exhibit distinct analgesic activity. Two of the most representative examples are: H HO O N CH3 O CH3 O HO O acetaminophen (Tylenol) acetylsalicylic acid (Aspirin) ======================================================================= The reaction to be carried out in this experiment is: Acetylation of aniline δ- H3C δ+ O acetic O O anhydride H N CH3 N H (electrophile) HO O CH3 + H O CH3 acetanilide acetic acid aniline (nucleophile) Both aniline and acetic anhydride are somewhat viscous liquids. So, simply mixing them together does not result in the efficient formation of acetanilide. Therefore, a solvent (in this case water) is used to dissolve and evenly disperse two reactants in it. R R R Note: O + N R" N R" N CH R' R' R' 3 CH3 - O O O acetyl group amide The amide N is usually not nucleophilic acetamide because of a significant contribution of this resonance form. Reaction mechanism: δ- H H3C H H H3C δ+ O H N O H O N O CH3 O O N + O O H CH3 O CH3 CH3 pKa ~ -5 3 O CH3 tetrahedral (sp ) intermediate B (including ) O H N CH3 O acetanilide Chem 216 S11 Notes - Dr. Masato Koreeda Date: May 3, 2011 Topic: __Experiment 1____ page 2 of 2. Additional comments on the reaction mechanism: 1.
    [Show full text]
  • Sodium Acetate
    SODIUM ACETATE Prepared at the 18th JECFA (1974), published in NMRS 54B (1975) and in FNP 52 (1992). Metals and arsenic specifications revised at the 59th JECFA (2002). An ADI not limited' was established at the 17th JECFA (1973) SYNONYMS INS No. 262(i) DEFINITION Chemical names Sodium acetate C.A.S. number 127-09-3 Chemical formula C2H3NaO2 · nH2O (n = 0 or 3) Structural formula CH3COONa · nH2O (n = 0 or 3) Formula weight Anhydrous: 82.03 Trihydrate: 136.08 Assay Not less than 98.5% after drying DESCRIPTION Anhydrous: White, odourless, granular, hygroscopic powder Trihydrate: Colourless, transparent crystals or a granular crystalline powder, odourless or with a faint, acetic odour. Effloresces in warm, dry air. FUNCTIONAL USES Buffer CHARACTERISTICS IDENTIFICATION Solubility (Vol. 4) Very soluble in water; soluble in ethanol pH (Vol. 4) 8.0 - 9.5 (1 in 100 soln) Test for sodium (Vol. 4) Passes test Test for acetate (Vol. 4) Passes test Heat test Anhydrous: When heating the sample slowly, it first fuses gradually and boils, and later decomposes evolving an unpleasant odour of acetone. A solution of the residue gives alkaline reaction with litmus paper. Trihydrate: When heating the sample slowly, it liquefies. Then water evaporates, and a powder forms. By heating more strongly, the powder fuses, and becomes lumpy and later decomposes evolving an odour of acetone. A solution of the residue gives alkaline reaction with litmus paper. PURITY Loss on drying (Vol. 4) Anhydrous: Not more than 2.0% (120o, 4 h) Trihydrate: Between 36 and 42% (120o, 4 h) Test for potassium Negative test (Vol.
    [Show full text]
  • Compare 1 L of Acetate Buffer Solution (0.50 Mol of Acetic Acid and 0.50 Mol Sodium Acetate) to 1 L of Hcl Solution
    Compare 1 L of acetate buffer solution (0.50 mol of acetic acid and 0.50 mol sodium acetate) to 1 L of HCl solution + + H AcOH + + + H - - H + H H AcO AcO + H - H + Cl AcOH - H AcOH AcO - - + AcO AcOH + - Cl - H - H Cl Cl AcOH AcO - - - + AcOH AcOH - + Cl Cl Cl H - AcO H AcO AcOHAcOH - - AcO = CH 3 CO 2 The acetate solution was made by dissolving 0.50 mol of acetic acid and 0.50 mol sodium acetate in 1 liter of water; at equilibrium [H+] = 1.8 x 10-5 M. The HCl solution was made by dissolving 1.8 x 10-5 mol of HCl in 1 liter of water. Similarities The pH of each of these solutions is the same; that is, the [H+] is the same in both beakers (go ahead and count). Differences The total amount of acid pesent is not the same. [H+] is the same (1.8 x 10-5 M), but the acetate buffer contains additional acid in the form of undissociated acetic acid (0.50 M). The amount of base present is not the same. The HCl solution does not contain a base; Cl– is the conjugate base, but the conjugate base of a strong acid does not act like a base. – The acetate buffer does contain a base; CH3CO2 is the conjugate base, and the conjugate base of a weak acid is a weak base. 125 What happens when base is added to each flask. Say, 0.001 mol NaOH. The following reaction occurs + – H (aq) + OH (aq) H2O (l) So, the H+ is consumed by the OH–.
    [Show full text]
  • Chemical Names and CAS Numbers Final
    Chemical Abstract Chemical Formula Chemical Name Service (CAS) Number C3H8O 1‐propanol C4H7BrO2 2‐bromobutyric acid 80‐58‐0 GeH3COOH 2‐germaacetic acid C4H10 2‐methylpropane 75‐28‐5 C3H8O 2‐propanol 67‐63‐0 C6H10O3 4‐acetylbutyric acid 448671 C4H7BrO2 4‐bromobutyric acid 2623‐87‐2 CH3CHO acetaldehyde CH3CONH2 acetamide C8H9NO2 acetaminophen 103‐90‐2 − C2H3O2 acetate ion − CH3COO acetate ion C2H4O2 acetic acid 64‐19‐7 CH3COOH acetic acid (CH3)2CO acetone CH3COCl acetyl chloride C2H2 acetylene 74‐86‐2 HCCH acetylene C9H8O4 acetylsalicylic acid 50‐78‐2 H2C(CH)CN acrylonitrile C3H7NO2 Ala C3H7NO2 alanine 56‐41‐7 NaAlSi3O3 albite AlSb aluminium antimonide 25152‐52‐7 AlAs aluminium arsenide 22831‐42‐1 AlBO2 aluminium borate 61279‐70‐7 AlBO aluminium boron oxide 12041‐48‐4 AlBr3 aluminium bromide 7727‐15‐3 AlBr3•6H2O aluminium bromide hexahydrate 2149397 AlCl4Cs aluminium caesium tetrachloride 17992‐03‐9 AlCl3 aluminium chloride (anhydrous) 7446‐70‐0 AlCl3•6H2O aluminium chloride hexahydrate 7784‐13‐6 AlClO aluminium chloride oxide 13596‐11‐7 AlB2 aluminium diboride 12041‐50‐8 AlF2 aluminium difluoride 13569‐23‐8 AlF2O aluminium difluoride oxide 38344‐66‐0 AlB12 aluminium dodecaboride 12041‐54‐2 Al2F6 aluminium fluoride 17949‐86‐9 AlF3 aluminium fluoride 7784‐18‐1 Al(CHO2)3 aluminium formate 7360‐53‐4 1 of 75 Chemical Abstract Chemical Formula Chemical Name Service (CAS) Number Al(OH)3 aluminium hydroxide 21645‐51‐2 Al2I6 aluminium iodide 18898‐35‐6 AlI3 aluminium iodide 7784‐23‐8 AlBr aluminium monobromide 22359‐97‐3 AlCl aluminium monochloride
    [Show full text]
  • Trna Northern Analysis
    tRNA Northern Analysis Brian Jester ( [email protected] ) Université de Strasbourg Method Article Keywords: tRNA Posted Date: May 3rd, 2011 DOI: https://doi.org/10.1038/protex.2011.223 License: This work is licensed under a Creative Commons Attribution 4.0 International License. Read Full License Page 1/4 Abstract This protocol provides a means to dene the level of aminoacylation for a specic tRNA in vivo. Introduction Herein describes a method for extracting total RNA from a cell, resolving the charged and uncharged species by electrophoresis and the blotting/detection of a specic tRNA species. Reagents LB media Sodium Acetate 0.3M \(pH 4.5), 10 mM EDTA. sodium acetate 10 mM \(pH4.5) sodium acetate 1.0 M \(pH 5.0) sodium acetate 0.3 M \(pH5.0) etoH phenol:chloroform \(pH 4.7) 40% polyacrylamide \ (19:1) urea 100 mM Tris-Hcl, 100 mM NaCl pH 9.5 1.0 M Tris-Oac pH 7.8 EDTA \(0.5 M pH 8.0) Equipment incubator to grow culture centrifuge microfuge vortex spectrophotometer agarose gel electrophoresis BioRad miniprotein II rig for gel running/blotting hot water bath UV crosslinker hybridization oven Procedure **Culture Growth \(_B. subtilis_)** 1. Grow an overnight 5.0 ml LB culture of the strains to be evaluated. 2. Inoculate the overnights to 30 ml LB and do a short growth curve to get the cells at mid log-phase \ (OD600 = 0.5). 3. Pellet cells at 5k, 5 min., 4∞C. All steps and solutions from here forward are to be on ice. 4.
    [Show full text]
  • Cbc Storeroom Chemical Price Listing
    CBC STOREROOM CHEMICAL PRICE LISTING PRODUCT NAME PRODUCT CODE SIZE PRICE LOCATION 1 . ACETIC ACID A38S-212 2.5 LT $34.75 23C1 2 . ACETIC ACID A38-500 500 ML $23.75 23B1 3 . ACETIC ACID, MACRON CHEMIC MKV19318 2.5L $85.25 23D1 4 . ACETIC ANHYDRIDE A10-500 500 ML $32.75 RRC1 5 . ACETONE ACS A18P-4 4 LT $46.50 RRB1 6 . ACETONE HISTOLOGICAL A16P-4 4 LT $38.50 RRA1 7 . ACETONITRILE HPLC A998-1 1 LT $41.25 RRC1 8 . ACETONITRILE HPLC A998-4 4 LT $75.25 RRC1 9 . ALCOHOL HPLC GRADE DENATU A995-4 4 LT $26.25 RRD2 10 . ALUMINA, BASIC, 60-325 MESH A941-500 500G $64.75 SPECIAL ORDER 11 . ALUMINA, NEUTRAL, 60-325 ME A950-500 500G $101.95 SPECIAL ORDER 12 . ALUMINUM CHLORIDE A573-500 500 G $50.00 06A1 13 . ALUMINUM NITRATE A586-250 250 G $28.50 13A1 14 . ALUMINUM NITRATE A586-500 500 G $49.50 13A2 15 . AMMONIUM BICARBONATE A643-500 500 G $33.00 06A2 16 . AMMONIUM CHLORIDE A661-3 3 KG $53.85 06B1 17 . AMMONIUM CHLORIDE A661-500 500 G $29.25 06B2 18 . AMMONIUM DICHROMATE A644-500 500 G $55.00 13A3 19 . AMMONIUM HYDROXIDE A669S-212 2.5 LT $39.50 12A1 20 . AMMONIUM HYDROXIDE A669-500 500 ML $30.75 12A2 21 . AMMONIUM NITRATE A676-500 500 G $37.50 13A4 22 . AMMONIUM SULFATE A702-500 500 G $25.75 06B3 23 . AMYL ALCOHOL, N- A394-500 500 ML $31.75 RRC1 24 . ARGON GAS CYLINDER AR 200X CHEM OWNED $25.50 CYLINDER WALL 25 .
    [Show full text]
  • Nucleic Acid Precipitation from Dilute Solutions
    Protocol TD-P Revision 2.0 Creation Date: 6/10/2015 Revision Date: 3/6/2019 Nucleic Acid Precipitation from Dilute Solutions Introduction Glycogen is also an inert carrier used to increase nucleic acid recovery from alcohol precipitation. It is a preferred coprecipitant for solutions containing oligonucleotides or low concentrations of DNA or RNA, as it does not add exogenous nucleic acids like other coprecipitants, such as yeast RNA or tRNA. Glycogen, a highly purified branched chain carbohydrate, is insoluble in ethanol and isopropanol and forms a precipitate that traps nucleic acids. Upon centrifugation, the insoluble glycogen/nucleic acid precipitate forms a visible pellet that simplifies downstream sample processing. Glycogen, 20 mg/ml, may be used for the recovery of oligonucleotides (>8 bases) and low amounts of nucleic acids (≥20 pg) from diluted solutions. Materials Nucleic acid solution Glycogen, 20 mg/ml (GoldBio Catalog # G-090) 3M Sodium Acetate, pH 5.2 Isopropanol or ethanol Nuclease-free water or TE Buffer, pH 8 Method 1. Add 1/10 volume of 3M sodium acetate, pH 5.2 to the nucleic acid in solution. Note: 1/10 volume of 2M sodium chloride or 5M ammonium acetate may be substituted. 2. Add Glycogen Solution, 20 mg/ml to final concentration of 0.05-1 µg/µl. Note: For oligonucleotides, use a final concentration of 1 µg/µl. For DNA or RNA, use a final concentration of 0.05-1 µg/µl of Glycogen Solution. 3. Add 1 volume of isopropanol to the solution. Mix gently. Note: 2.5 volumes of ethanol may be substituted.
    [Show full text]
  • Buffer Solutions
    Buffer Solutions pH of solution adding 0.10 M HCl to 100 mL water HCl added pH 7 0 mL 7.00 6 2 mL 2.71 5 5 mL 2.32 4 10 mL 2.04 3 20 mL 1.78 2 50 mL 1.48 1 0 1020304050 mL of 0.10 M HCl added Buffer Solutions ν A buffer helps a solution maintain its pH when acid or base is added ν A buffer must contain two components to work ν a weak acid that reacts with added base ν a weak base that reacts with added acid ν Buffers usually contain approximately equal amounts of a weak acid and its conjugate base 1 Buffer Solutions Solution that is 0.100 M CH3COOH (acetic acid) and 0.100 M NaCH3COO (sodium acetate) Find pH of buffer solution: ↔ - + CH3COOH(aq) + H2O CH3COO (aq) + H3O (aq) - + [CH3COOH] [CH3COO ] [H3O ] initial 0.100 0.100 ≈0 -x x x equil 0.100 – x 0.100 + x x Buffer Solutions Find pH of buffer solution: ↔ - + CH3COOH(aq) + H2O CH3COO (aq) + H3O (aq) - + + = [CH3COO ][H3O ] = (.100 x)x = -5 Ka 1.8 x 10 [CH 3COOH ] (.100 - x) assume x is negligible compared to .100 M x = 1.80 x 10-5 M pH = 4.74 2 Buffer Solutions Add 5 mL .10 M HCl Find pH of resulting solution Assume all acid added reacts with acetate ion to form acetic acid (remember that acids react with bases) ↔ - + CH3COOH(aq) + H2O CH3COO (aq) + H3O (aq) + -3 [H3O ] added = (5 mL)(.10 M)/(105 mL) = 4.76x10 M [CH3COOH] = 0.100 + 0.005 = 0.105 M - [CH3COO ] = 0.100 - 0.005 = 0.095 M Buffer Solutions Now let solution come to equilibrium - + [CH3COOH] [CH3COO ] [H3O ] initial .105 .095 ≈0 -x x x equil .105 – x .095 + x x - + + = [CH3COO ][H3O ] = (.095 x)x = -5 Ka 1.8 x 10 [CH 3COOH
    [Show full text]
  • Reaction Rate and Rate Constant of the Hydrolysis of Ethyl Acetate With
    AMERICAN JOURNAL OF SCIENTIFIC AND INDUSTRIAL RESEARCH © 2015,Science Huβ, http://www.scihub.org/AJSIR ISSN: 2153-649X, doi:10.5251/ajsir.2015.6.1.1.4 Reaction rate and rate constant of the hydrolysis of ethyl acetate with sodium hydroxide Ikhazuangbe, Prosper Monday Ohien and Oni, Aisosa Babalola Madonna university, Faculty of Engineering Chemical Engineering Department, P.m.b 302 Enugu, Nigeria ABSTRACT Hydrolysis is a chemical decomposition involving breaking of a bond and the addition of elements of water. In this hydrolysis of ester (ethyl acetate) with an alkali (sodium hydroxide), HCl was used as catalyst to accelerate it. 1ml and 2ml of ethyl acetate was injected separately into the 500ml reactor vessels which contains 0.05N of NaOH and thoroughly mixed. At regular time interval, 0, 10, 20, 30, 40, and 90 minutes, 25ml of each of the samples were withdrawn into a 250ml conical flask containing 0.05N HCl, and titrated against 0.05N NaOH solution using phenolphthalein as indicator. From the titre values, the hydrolysis involving the 1ml ethyl acetate was faster than that of the 2ml ethyl acetate, indicating that the higher the concentration the faster the rate of reaction. The rate constant after evaluation from the graphs was approximately 0.003min-1cm-3 for the 1ml and 2ml ethyl acetate, signifying that while the rate of reaction is concentration dpendent, the rate constant is not dependent on concentration Key words: Alkali, concentration, ester, hydrolysis and reactor INTRODUCTION product is formed. The rate at which the reactant ‘a’ is disappearing is proportional to its concentration at Chemical reaction takes place when a detectable any instance, number of molecules of one or more species have lost their identity and assumed a new form by a I.e.
    [Show full text]
  • 1 Binding of Divalent Cations to Acetate
    Binding of Divalent Cations to Acetate: Molecular Simulations Guided by Raman Spectroscopy Denilson Mendes de Oliveira1, Samual R. Zukowski1, Vladimir Palivec2, Jérôme Hénin3,4, 2 1* 2* 2,3,4* Hector Martinez Seara , Dor Ben-Amotz , Pavel Jungwirth , Elise Duboué-Dijon 1 Department of Chemistry, Purdue University, West Lafayette, Indiana 47907 2 Institute of Organic Chemistry and Biochemistry, Academy of Sciences of the Czech Republic, Flemingovo nám. 2, 16610 Prague 6, Czech Republic 3CNRS, Université de Paris, UPR 9080, Laboratoire de Biochimie Théorique, 13 rue Pierre et Marie Curie, 75005, Paris, France 4 Institut de Biologie Physico-Chimique-Fondation Edmond de Rothschild, PSL Research University, Paris, France *email: [email protected]; [email protected]; [email protected] Abstract In spite of the biological importance of the binding of Zn2+, Ca2+, and Mg2+ to the carboxylate group, cation-acetate binding affinities and binding modes remain actively debated. Here, we report the first use of Raman multivariate curve resolution (Raman-MCR) vibrational spectroscopy to obtain self-consistent free and bound metal acetate spectra and one-to-one binding constants, without the need to invoke any a priori assumptions regarding the shapes of the corresponding vibrational bands. The experimental results, combined with classical molecular dynamics simulations with a force field effectively accounting for electronic polarization via charge scaling and ab initio simulations, indicate that the measured binding constants pertain to direct (as opposed to water separated) ion pairing. The resulting binding constants do not scale with cation size, as 1 the binding constant to Zn2+ is significantly larger than that to either Mg2+ or Ca2+, although Zn2+ and Mg2+ have similar radii that are about 25% smaller than Ca2+.
    [Show full text]