DOCSLIB.ORG

Buffer Solutions

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Buffer Solutions Buffer Solutions pH of solution adding 0.10 M HCl to 100 mL water HCl added pH 7 0 mL 7.00 6 2 mL 2.71 5 5 mL 2.32 4 10 mL 2.04 3 20 mL 1.78 2 50 mL 1.48 1 0 1020304050 mL of 0.10 M HCl added Buffer Solutions ν A buffer helps a solution maintain its pH when acid or base is added ν A buffer must contain two components to work ν a weak acid that reacts with added base ν a weak base that reacts with added acid ν Buffers usually contain approximately equal amounts of a weak acid and its conjugate base 1 Buffer Solutions Solution that is 0.100 M CH3COOH (acetic acid) and 0.100 M NaCH3COO (sodium acetate) Find pH of buffer solution: ↔ - + CH3COOH(aq) + H2O CH3COO (aq) + H3O (aq) - + [CH3COOH] [CH3COO ] [H3O ] initial 0.100 0.100 ≈0 -x x x equil 0.100 – x 0.100 + x x Buffer Solutions Find pH of buffer solution: ↔ - + CH3COOH(aq) + H2O CH3COO (aq) + H3O (aq) - + + = [CH3COO ][H3O ] = (.100 x)x = -5 Ka 1.8 x 10 [CH 3COOH ] (.100 - x) assume x is negligible compared to .100 M x = 1.80 x 10-5 M pH = 4.74 2 Buffer Solutions Add 5 mL .10 M HCl Find pH of resulting solution Assume all acid added reacts with acetate ion to form acetic acid (remember that acids react with bases) ↔ - + CH3COOH(aq) + H2O CH3COO (aq) + H3O (aq) + -3 [H3O ] added = (5 mL)(.10 M)/(105 mL) = 4.76x10 M [CH3COOH] = 0.100 + 0.005 = 0.105 M - [CH3COO ] = 0.100 - 0.005 = 0.095 M Buffer Solutions Now let solution come to equilibrium - + [CH3COOH] [CH3COO ] [H3O ] initial .105 .095 ≈0 -x x x equil .105 – x .095 + x x - + + = [CH3COO ][H3O ] = (.095 x)x = -5 Ka 1.8 x 10 [CH 3COOH ] (.105 - x) x = 1.99 x 10-5 M pH = 4.71 3 Buffer Solutions pH of buffered solution adding 0.10 M HCl to 100 mL soln 7 HCl added pH 6 0 mL 4.74 5 mL 4.71 5 Buffered solution 10 mL 4.66 4 15 mL 4.58 3 25 mL 4.57 2 1 50 mL 4.45 0 1020304050 mL of 0.10 M HCl added Buffer Solutions ν Henderson-Hasselbach Equation ν Allows calculation of pH of a buffer if concentrations of conjugate acid and conjugate base are known ↔ + - HA(aq) + H2O H3O (aq) + A (aq) [H O+ ][A-] K = 3 a [HA] + K [HA] [H O ] = a 3 [A-] 4 Buffer Solutions ν Take -log of both sides + ⎧ K [HA]⎫ ⎛ [HA]⎞ −log[H O ] = -log⎨ a ⎬ = - log() K -log⎜ ⎟ 3 ⎩ [A-] ⎭ a ⎝ [A-] ⎠ ⎛ [HA]⎞ ⎛ [A-] ⎞ -log(K ) = pK −log⎜ ⎟ = log⎜ ⎟ a a ⎝ [A− ]⎠ ⎝ [HA]⎠ ⎛ [A-] ⎞ pH = pK + log⎜ ⎟ Henderson-Hasselbach a ⎝ [HA]⎠ Eqn Buffer Solutions ν Using the Henderson-Hasselbach Eqn, we can: ν Determine pH of a solution ν Determine ratio of conjugate base to conjugate acid to achieve specific pH ⎛ [A-] ⎞ pH = pK + log⎜ ⎟ a ⎝ [HA]⎠ 5 Buffer Solutions ν Let’s go back to problem of adding HCl to buffer solution: ν We can use H-H eqn. to make the calculations much easier [CH3COOH] = 0.100 + [HCl]added - [CH3COO ] = 0.100 – [HCl]added ⎛ [A-] ⎞ pH = pK + log⎜ ⎟ a ⎝ [HA]⎠ Buffer Solutions - VHCl [HCl] [CH3COOH] [CH3COO ] pH 5mL (.1)(5mL)/105mL .100+.005 .100-.005 = .00476 M =.105 M =.095 M 4.70 10mL (.1)(10)/110 .100+.009 .100-.009 = .00909 M =.109 M =.091 M 4.66 25mL (.1)(25)/125 .100+.020 .100-.020 = .0200 M =.120 M =.080 M 4.56 50mL (.1)(50)/150 .100+.033 .100-.033 = .0333 M =.133 M =.067 M 4.44 6 Buffer Solutions ν Buffer Capacity—the amount of acid or base that can be added to a buffer without the pH significantly changing ν Suppose we acid to a buffer solution: ν The acid will react with the conjugate base until it is depleted ν Past this point, the solution behaves as if no buffer were present Acid-Base Titrations ν A titration is a method used to determine the concentration of an unknown species ν Add a measured amount of a known reactant ν Determine when the reaction has gone to completion [unknown] + [known] → products ν At the equivalence point moles unknown = moles known added CunknownVunknown = CknownVknown 7 Acid-Base Titrations Titrate 50.00 10 mL unknown 9 HCl soln. 8 equivalence point with 0.2137 7 M NaOH 6 5 4 3 2 1 0 5 10 15 20 25 30 35 40 mL NaOH added Acid-Base Titrations 10 At equivalence point, VNaOH = 23.96 mL 9 8 equivalence point mol(NaOH) = 7 (.2137 M)(.02396 L) 6 = 5.120 x 10-3 mol 5 4 -3 mol(HCl) = 5.120 x 10 mol 3 (mol known = mol unknown) 2 1 [HCl] = 0 5 10 15 20 25 30 35 40 (5.120x10-3 mol)/(.05000 L) mL NaOH added = 0.1024 M 8 Indicators ν An indicator is a chemical species that changes color depending on the pH of the solution ν An indicator is a conjugate acid-conjugate base pair in which the acid and base forms of the compound have different colors → - + HIn(aq) + H2O In (aq) + H3O (aq) color 1 color 2 ν Indicators are used to determine the endpoint of a titration Indicators ν The pKa of the indicator determines the pH range over which the color changes [HIn]/[In-] ≥ 10 acid color [HIn]/[In-] ″ 0.1 base color [HIn]/[In-] ≈ 1 intermediate color ν - Remember: pH = pKa + log{[In ]/[HIn]} If [HIn]/[In-] = 1, log{[HIn]/[In-]} = 0 ∴ pH = pKa at point when indicator is changing color 9 Indicators Indicator pKa pH range color change Methyl orange 3.7 3.1 – 4.4 red to yellow Bromophenol blue 4.0 3.0 – 4.6 yellow to blue Methyl red 5.1 4.2 – 6.3 red to yellow Bromothymol blue 7.0 6.0 – 7.6 yellow to blue Phenol red 7.9 6.8 – 8.4 yellow to red Phenolphthalein 9.3 8.2 – 10.0 clear to pink Indicators Figure 17.5: pH curve for change after endpoint titration of 0.100 M HCl with 0.100 M NaOH change around endpoint change before endpoint 10 Indicators ν Titration of weak acid with strong base - → - HA(aq) + OH (aq) A (aq) + H2O ν At equivalence point - ↔ - A (aq) + H2O HA(aq) + OH (aq) the solution is basic because conjugate base of weak acid reacts with water to form OH-(aq) Indicators ν Titrate 25.00 mL 0.100 M formic acid (HCOOH) with 0.100 M NaOH -4 Ka = 1.8 x 10 ν Find pH at equivalence point and select appropriate indicator ν At equivalence point, mol(HCOOH) = mol(OH-) mol(fa) = (0.100 M fa)(0.02500 L) = 2.5 x 10-3 mol fa = formic acid -3 VNaOH added = (2.5 x 10 mol)/(0.100 M) = 25.0 mL Vtotal = 50.0 mL 11 Indicators ν Assume HCOOH + OH- reaction goes to completion: [HCOO-] = (2.5 x 10-3 mol)/(0.0500 L) = 0.0500 M ν Determine Keq for reaction of formate ion: - ↔ - HCOO (aq) + H2O HCOOH(aq) + OH (aq) - = [HCOOH][OH ] = Kw = -11 Keq − 6.67 x 10 [HCOO ] Ka Indicators - = [HCOOH][OH ] = Kw = -11 Keq − 6.67 x 10 [HCOO ] Ka [HCOO-] [HCOOH] [OH-] initial .0500 0 0 -x x x equil .0500 – x x x [HCOOH][OH-] x2 K = = = 6.67 x 10-11 eq [HCOO-] 0.0500 − x 12 Indicators [HCOOH][OH-] x2 K = = = 6.67 x 10-11 eq [HCOO-] 0.0500 − x x = 1.83 x 10-6 M = [OH-] pOH = -log(1.83 x 10-6) =5.74 pH = 14.00 – 5.74 = 8.26 Phenol red (6.8 – 8.4) or phenolphthalein (8.2 – 10.0) would be appropriate indicators Indicators ν Titration of weak base with strong acid + → + B(aq) + H3O (aq) BH (aq) + H2O ν At equivalence point + ↔ + BH (aq) + H2O B(aq) + H3O (aq) the solution is acidic because conjugate acid of + weak base reacts with water to form H3O (aq) 13 Indicators Figure 17.8: titration of 0.100 M NH3 with 0.100 M HCl Acid Rain ν Carbon dioxide in the air is in equilibrium with H2O in atmospheric water droplets (clouds & fog): ↔ CO2(aq) + H2O H2CO3(aq) -7 carbonic acid Ka = 4.2 x 10 ↔ + - H2CO3(aq) + H2O H3O (aq) + HCO3 (aq) ν Natural rain water has pH = 5.6 14 Acid Rain ν Emitted pollutants can form additional acid sources in clouds: NO2: ↔ 2 NO2(aq) + H2O HNO3(aq) + HNO2(aq) nitric acid nitrous acid -4 strong Ka = 4.5 x 10 Acid Rain ν Emitted pollutants can form additional acid sources in clouds: SO2: ↔ SO2(aq) + H2O H2SO3(aq) -2 sulfurous acid Ka = 1.2 x 10 → 2 SO2(g) + O2(g) 2 SO3(g) ↔ SO3(aq) + H2O H2SO4(aq) sulfuric acid strong 15 Acid Rain Solubility Products ν Many salts are only slightly soluble ν The solubility product is a measure of the concentration of ions in a solution saturated with the salt ↔ + - + - MA(s) M (aq) + A (aq) Ksp = [M ][A ] Examples ↔ + - + - -10 AgCl(s) Ag (aq) + Cl (aq) Ksp=[Ag ][Cl ]=1.8x10 ↔ 2+ - 2+ - 2 -5 PbCl2(s) Pb (aq) + 2 Cl (aq) Ksp=[Pb ][Cl ] =1.7x10 ↔ 3+ - 3+ - 3 -36 AuBr3(s) Au (aq) + 3 Br (aq) Ksp=[Au ][Br ] =4.0x10 16 Solubility Products ν Knowing the Ksp, we can calculate the concentration of ions in solution Examples ↔ + - + - -10 AgCl(s) Ag (aq) + Cl (aq) Ksp=[Ag ][Cl ]=1.8x10 °-x x x x2 = 1.8 x 10-10 ⇒ x = 1.3 x 10-5 M = [Ag+] = [Cl-] Solubility Products Examples ↔ 2+ - 2+ - 2 -5 PbCl2(s) Pb (aq) + 2 Cl (aq) Ksp=[Pb ][Cl ] =1.7x10 °-x x 2x x(2x)2 = 1.7 x 10-5 4x3 = 1.7 x 10-5 ⇒ x = 1.6 x 10-2 M [Pb2+] = 1.6 x 10-2 M [Cl-] = 3.2 x 10-2 M 17 Solubility Products Examples ↔ 3+ - 3+ - 3 -36 AuBr3(s) Au (aq) + 3 Br (aq) Ksp=[Au ][Br ] =4.0x10 °-x x 3x x(3x)3 = 4.0 x 10-36 27x4 = 4.0 x 10-36 ⇒ x = 6.2 x 10-10 M [Au3+] = 6.2 x 10-10 M [Br-] = 1.9 x 10-9 M Solubility Products Examples—Common ion effect How much PbI2 will dissolve in a 0.0100 M solution of NaI? ↔ 2+ - -9 PbI2(s) Pb (aq) + 2 I (aq) Ksp = 8.7 x 10 °-x x 2x + .0100 x(2x+.0100)2 = 8.7 x 10-9 x(4x2 + 0.0200x + 1.0x10-4) = 8.7 x 10-9 4x3 + .0200x2 + 1.0x10-4x – 8.7x10-9 = 0 x = 8.6 x 10-5 M vs 1.3 x 10-3 M if no I-(aq) were present initially 18 Factors Affecting Solubility ν Salts that are slightly soluble in water can be much more soluble in acid if one or both of its ions are moderately basic: ↔ 2+ 2- -9 CaCO3(s) Ca (aq) + CO3 (aq) Ksp = 8.7 x 10 ν 2- - But CO3 (aq) is the conjugate base of HCO3 (aq) 2- + ↔ - -4 CO3 (aq) + H3O (aq) HCO3 (aq) + H2OKb = 2.1x10 - + ↔ -8 HCO3 (aq) + H3O (aq) H2CO3(aq) + H2OKb = 2.4x10 ↔ ≈ 5 H2CO3(aq) H2O + CO2(g) Keq 10 ν Works for carbonates, some sulfides, phosphates, etc.
Load more

Recommended publications
  • Choosing Buffers Based on Pka in Many Experiments, We Need a Buffer That Maintains the Solution at a Specific Ph. We May Need An
    Choosing buffers based on pKa In many experiments, we need a buffer that maintains the solution at a specific pH. We may need an acidic or a basic buffer, depending on the experiment. The Henderson-Hasselbalch equation can help us choose a buffer that has the pH we want. pH = pKa + log([conj. base]/[conj. acid]) With equal amounts of conjugate acid and base (preferred so buffers can resist base and acid equally), then … pH = pKa + log(1) = pKa + 0 = pKa So choose conjugates with a pKa closest to our target pH. Chemistry 103 Spring 2011 Example: You need a buffer with pH of 7.80. Which conjugate acid-base pair should you use, and what is the molar ratio of its components? 2 Chemistry 103 Spring 2011 Practice: Choose the best conjugate acid-base pair for preparing a buffer with pH 5.00. What is the molar ratio of the buffer components? 3 Chemistry 103 Spring 2011 buffer capacity: the amount of strong acid or strong base that can be added to a buffer without changing its pH by more than 1 unit; essentially the number of moles of strong acid or strong base that uses up all of the buffer’s conjugate base or conjugate acid. Example: What is the capacity of the buffer solution prepared with 0.15 mol lactic acid -4 CH3CHOHCOOH (HA, Ka = 1.0 x 10 ) and 0.20 mol sodium lactate NaCH3CHOHCOO (NaA) and enough water to make 1.00 L of solution? (from previous lecture notes) 4 Chemistry 103 Spring 2011 Review of equivalence point equivalence point: moles of H+ = moles of OH- (moles of acid = moles of base, only when the acid has only one acidic proton and the base has only one hydroxide ion).
    [Show full text]
  • Buffers a Guide for the Preparation and Use of Buffers in Biological Systems Calbiochem® Buffers a Guide for the Preparation and Use of Buffers in Biological Systems
    Buffers A guide for the preparation and use of buffers in biological systems Calbiochem® Buffers A guide for the preparation and use of buffers in biological systems Chandra Mohan, Ph.D. EMD, San Diego, California © EMD, an affiliate of Merck KGaA, Darmstadt, Germany. All rights reserved. A word to our valued customers We are pleased to present to you the newest edition of Buffers: A Guide for the Preparation and Use of Buffers in Biological Systems. This practical resource has been especially revamped for use by researchers in the biological sciences. This publication is a part of our continuing commitment to provide useful product information and exceptional service to you, our customers. You will find this booklet a highly useful resource, whether you are just beginning your research work or training the newest researchers in your laboratory. Over the past several years, EMD Biosciences has clearly emerged as a world leader in providing highly innovative products for your research needs in Signal Transduction, including the areas of Cancer Biology, Alzheimer’s Disease, Diabetes, Hypertension, Inflammation, and Apoptosis. Please call us today for a free copy of our LATEST Catalog that includes tools for signal transduction and life science research. If you have used our products in the past, we thank you for your support and confidence in our products, and if you are just beginning your research career, please call us and give us the opportunity to demonstrate our exceptional customer and technical service. Corrine Fetherston Sr. Director, Marketing ii Table of Contents: Why does Calbiochem® Biochemicals Publish a Booklet on Buffers? .
    [Show full text]
  • AMMONIA BUFFER SOLUTION MSDS CAS-No
    AMMONIA BUFFER SOLUTION MSDS CAS-No.: MSDS MATERIAL SAFETY DATA SHEET (MSDS) SECTION 1: Identification of the substance/mixture and of the company/undertaking 1.1. Product identifier Product form : Mixture : Product code : 01077 1.2. Relevant identified uses of the substance or mixture and uses advised against 1.2.1. Relevant identified uses Use of the substance/mixture : Laboratory chemicals, Manufacture of substances 1.2.2. Uses advised against No additional information available 1.3. Details of the supplier of the safety data sheet LOBA CHEMIE PVT.LTD. 107 Wode House Road, Jehangir Villa, Colaba 400005 Mumbai - INDIA T +91 22 6663 6663 - F +91 22 6663 6699 [email protected] - www.lobachemie.com 1.4. Emergency telephone number Emergency number : + 91 22 6663 6663 (9:00am - 6:00 pm) SECTION 2: Hazards identification 2.1. Classification of the substance or mixture Classification according to Regulation (EC) No. 1272/2008 [CLP]Mixtures/Substances: SDS EU 2015: According to Regulation (EU) 2015/830 (REACH Annex II) Skin corrosion/irritation, H314 Category 1B Specific target organ H335 toxicity — Single exposure, Category 3, Respiratory tract irritation Hazardous to the aquatic H400 environment — Acute Hazard, Category 1 Full text of hazard classes and H-statements : see section 16 Adverse physicochemical, human health and environmental effects No additional information available www.lobachemie.com 21/04/2016 1/9 AMMONIA BUFFER SOLUTION Safety Data Sheet according to Regulation (EC) No. 1907/2006 (REACH) with its amendment Regulation (EU) 2015/830 2.2. Label elements Labelling according to Regulation (EC) No. 1272/2008 [CLP] Extra labelling to displayExtra classification(s) to display Hazard pictograms (CLP) : GHS05 GHS07 GHS09 Signal word (CLP) : Danger Hazard statements (CLP) : H314 - Causes severe skin burns and eye damage.
    [Show full text]
  • Methanogenesis Rates in Acetate and Nitrate Amended Anoxic Slurries
    Methanogenesis rates in acetate and nitrate amended anoxic slurries BIOS 35502: Practicum in Environmental Field Biology Patrick Revord Advisor: William West 2011 Abstract With increasing urbanization and land use changes, pollution of lakes and wetland ecosystems is imminent. Any influx of nutrients, anthropogenic or natural, can have dramatic effects on lake gas production and flux. However, the net effect of simultaneous increase of both acetate and nitrate is unknown. Methane (CH4) production was measured in anoxic sediment and water slurries amended with ammonium nitrate (NH4NO3), which has been shown to inhibit methanogenesis, and sodium acetate (CH3COONa or NaOAc), which is known to increase methanogenesis. The addition of acetate significantly increased the methanogenesis rate, but the nitrate amendment had no significant effect. The simultaneous amendment of both acetate and nitrate showed no significant increase in CH4 compared to the control, indicating that the presence of nitrate may have reduced the effect of acetate amendment. Introduction Methane, a greenhouse gas associated with global warming, continues to increase in concentration in our atmosphere. Global yearly flux of methane into the atmosphere is 566 teragrams of CH4 per year, which is more than double pre-industrial yearly flux (Solomon et al. 2007). Increasing urbanization and land-use changes contribute significantly to increased gas levels (Anderson et al. 2010, Vitousek 1994). Nutrients travel from anthropogenic sources such as wastewater treatment facilities, landfills, and agricultural plots into nearby lakes, rivers, and wetlands, causing increased primary productivity in a process known as eutrophication (Vitousek et al. 1997). The increased nutrients and productivity lead to toxic algal blooms that create products such as acetate, H2, and CO2; a nutrient-rich anoxic environment suitable for anaerobic bacteria to produce unnaturally high levels of methane and other greenhouse gases (Davis and Koop 2006, West unpublished data).
    [Show full text]
  • NMR Chemical Shifts of Common Laboratory Solvents As Trace Impurities
    7512 J. Org. Chem. 1997, 62, 7512-7515 NMR Chemical Shifts of Common Laboratory Solvents as Trace Impurities Hugo E. Gottlieb,* Vadim Kotlyar, and Abraham Nudelman* Department of Chemistry, Bar-Ilan University, Ramat-Gan 52900, Israel Received June 27, 1997 In the course of the routine use of NMR as an aid for organic chemistry, a day-to-day problem is the identifica- tion of signals deriving from common contaminants (water, solvents, stabilizers, oils) in less-than-analyti- cally-pure samples. This data may be available in the literature, but the time involved in searching for it may be considerable. Another issue is the concentration dependence of chemical shifts (especially 1H); results obtained two or three decades ago usually refer to much Figure 1. Chemical shift of HDO as a function of tempera- more concentrated samples, and run at lower magnetic ture. fields, than today’s practice. 1 13 We therefore decided to collect H and C chemical dependent (vide infra). Also, any potential hydrogen- shifts of what are, in our experience, the most popular bond acceptor will tend to shift the water signal down- “extra peaks” in a variety of commonly used NMR field; this is particularly true for nonpolar solvents. In solvents, in the hope that this will be of assistance to contrast, in e.g. DMSO the water is already strongly the practicing chemist. hydrogen-bonded to the solvent, and solutes have only a negligible effect on its chemical shift. This is also true Experimental Section for D2O; the chemical shift of the residual HDO is very NMR spectra were taken in a Bruker DPX-300 instrument temperature-dependent (vide infra) but, maybe counter- (300.1 and 75.5 MHz for 1H and 13C, respectively).
    [Show full text]
  • Solvent Effects on the Thermodynamic Functions of Dissociation of Anilines and Phenols
    University of Wollongong Research Online University of Wollongong Thesis Collection 1954-2016 University of Wollongong Thesis Collections 1982 Solvent effects on the thermodynamic functions of dissociation of anilines and phenols Barkat A. Khawaja University of Wollongong Follow this and additional works at: https://ro.uow.edu.au/theses University of Wollongong Copyright Warning You may print or download ONE copy of this document for the purpose of your own research or study. The University does not authorise you to copy, communicate or otherwise make available electronically to any other person any copyright material contained on this site. You are reminded of the following: This work is copyright. Apart from any use permitted under the Copyright Act 1968, no part of this work may be reproduced by any process, nor may any other exclusive right be exercised, without the permission of the author. Copyright owners are entitled to take legal action against persons who infringe their copyright. A reproduction of material that is protected by copyright may be a copyright infringement. A court may impose penalties and award damages in relation to offences and infringements relating to copyright material. Higher penalties may apply, and higher damages may be awarded, for offences and infringements involving the conversion of material into digital or electronic form. Unless otherwise indicated, the views expressed in this thesis are those of the author and do not necessarily represent the views of the University of Wollongong. Recommended Citation Khawaja, Barkat A., Solvent effects on the thermodynamic functions of dissociation of anilines and phenols, Master of Science thesis, Department of Chemistry, University of Wollongong, 1982.
    [Show full text]
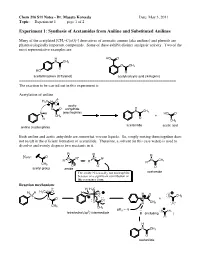
  • Experiment 1: Synthesis of Acetamides from Aniline and Substituted Anilines
    Chem 216 S11 Notes - Dr. Masato Koreeda Date: May 3, 2011 Topic: __Experiment 1____ page 1 of 2. Experiment 1: Synthesis of Acetamides from Aniline and Substituted Anilines Many of the acetylated [CH3–C(=O)-] derivatives of aromatic amines (aka anilines) and phenols are pharmacologically important compounds. Some of these exhibit distinct analgesic activity. Two of the most representative examples are: H HO O N CH3 O CH3 O HO O acetaminophen (Tylenol) acetylsalicylic acid (Aspirin) ======================================================================= The reaction to be carried out in this experiment is: Acetylation of aniline δ- H3C δ+ O acetic O O anhydride H N CH3 N H (electrophile) HO O CH3 + H O CH3 acetanilide acetic acid aniline (nucleophile) Both aniline and acetic anhydride are somewhat viscous liquids. So, simply mixing them together does not result in the efficient formation of acetanilide. Therefore, a solvent (in this case water) is used to dissolve and evenly disperse two reactants in it. R R R Note: O + N R" N R" N CH R' R' R' 3 CH3 - O O O acetyl group amide The amide N is usually not nucleophilic acetamide because of a significant contribution of this resonance form. Reaction mechanism: δ- H H3C H H H3C δ+ O H N O H O N O CH3 O O N + O O H CH3 O CH3 CH3 pKa ~ -5 3 O CH3 tetrahedral (sp ) intermediate B (including ) O H N CH3 O acetanilide Chem 216 S11 Notes - Dr. Masato Koreeda Date: May 3, 2011 Topic: __Experiment 1____ page 2 of 2. Additional comments on the reaction mechanism: 1.
    [Show full text]
  • Buffers and Buffer Capacity
    BUFFERS AND BUFFER CAPACITY By Dr. Jan Pláteník Principle of buffering A buffer solution is a solution that resists changes in pH either when diluted or when limited amounts of acid or base are added to it. Such a solution can be prepared by combining a weak acid and its salt with a strong base (conjugated base) or, analogously, a weak base and its salt with a strong acid (conjugated acid). For example: Acetate buffer : CH 3COOH (the weak acid) + CH 3COONa (the salt, conjugated base) Phosphate buffer : NaH 2PO 4 (the weak acid) + Na 2HPO 4 (the salt, conjugated base) Tris buffer: (Tris: Tris [2-amino-2-(hydroxymethyl)-propan-1,3-diol)] , an organic base) The Henderson-Hasselbalch equation describes the behavior of such a buffer and for the mixture of a weak acid and its salt with a strong base (conjugated base) it has the form: cs pH = pK a + log cac pK a negative logarithm of the dissociation constant for the weak acid, cs substance concentration of the salt (conjugated base), cac substance concentration of the weak acid (conjugated acid). Graphically the Henderson-Hasselbalch equation plotted as the acid : conjugated base ratio vs. pH of buffer actually constitutes the titration curve of the weak acid (see figure on the next page). Note also that for the acid : base ratio 1:1 the pH of buffer just equals the pK a (this is valid for uni-univalent systems, e.g., CH 3COOH/CH 3COONa, NaH 2PO 4/Na 2HPO 4). 1 Titration curve of sodium phosphate buffer 10 9 8 pH = pKa = 7.21 7 pHof buffer 6 5 9:1 8:2 7:3 6:4 1:1 4:6 3:7 2:8 1:9 Acid : base ratio The equation for a weak base and its salt with a strong acid (conjugated acid) has the form: cb pH = pK w − pK b + log cs pK b negative logarithm of the dissociation constant for the weak base, cb substance concentration of the base, cs substance concentration of the salt (conjugated acid), -14 pK w = 14 = − log 10 (ionic product of water).
    [Show full text]
  • Sodium Acetate
    SODIUM ACETATE Prepared at the 18th JECFA (1974), published in NMRS 54B (1975) and in FNP 52 (1992). Metals and arsenic specifications revised at the 59th JECFA (2002). An ADI not limited' was established at the 17th JECFA (1973) SYNONYMS INS No. 262(i) DEFINITION Chemical names Sodium acetate C.A.S. number 127-09-3 Chemical formula C2H3NaO2 · nH2O (n = 0 or 3) Structural formula CH3COONa · nH2O (n = 0 or 3) Formula weight Anhydrous: 82.03 Trihydrate: 136.08 Assay Not less than 98.5% after drying DESCRIPTION Anhydrous: White, odourless, granular, hygroscopic powder Trihydrate: Colourless, transparent crystals or a granular crystalline powder, odourless or with a faint, acetic odour. Effloresces in warm, dry air. FUNCTIONAL USES Buffer CHARACTERISTICS IDENTIFICATION Solubility (Vol. 4) Very soluble in water; soluble in ethanol pH (Vol. 4) 8.0 - 9.5 (1 in 100 soln) Test for sodium (Vol. 4) Passes test Test for acetate (Vol. 4) Passes test Heat test Anhydrous: When heating the sample slowly, it first fuses gradually and boils, and later decomposes evolving an unpleasant odour of acetone. A solution of the residue gives alkaline reaction with litmus paper. Trihydrate: When heating the sample slowly, it liquefies. Then water evaporates, and a powder forms. By heating more strongly, the powder fuses, and becomes lumpy and later decomposes evolving an odour of acetone. A solution of the residue gives alkaline reaction with litmus paper. PURITY Loss on drying (Vol. 4) Anhydrous: Not more than 2.0% (120o, 4 h) Trihydrate: Between 36 and 42% (120o, 4 h) Test for potassium Negative test (Vol.
    [Show full text]
  • CHAPTER 17: Advanced Acid-Base Equilibria
    Chapter 17 Advanced Acid-Base Equilibria SY 4/12/11 CHAPTER 17: Advanced Acid-Base Equilibria Chapter 17 17.1 Acid-Base Reactions 17.2 Buffers 17.3 Acid-Base Titrations Chapter In Context 17.4 Polyprotic Acids We will now expand the introductory coverage of acid-base equilibria in the previous 17.5 Two Important Buffer Systems chapter and explore the chemistry of more complicated aqueous solutions containing acids and bases. First we will address the different types of acid-base reactions and then move on to study buffer solutions, acid-base titrations, and polyprotic acids. So that you can get a feeling for the importance of buffers in your world, we will also briefly discuss Chapter Goals the chemistry of two important buffers in biological systems. In the following chapter Recognize the different we will conclude our coverage of chemical equilibria with Lewis acids and bases and the types of and the extent equilibria of sparingly soluble compounds. of acid-base reactions. Describe the One of the more important types of acid-base solutions in terms of commercial and components of a buffer. biological applications are buffers because they allow us to control the pH of a solution. Apply the principles of Buffers play an important role wherever you look: acid-base equilibria to Biology: You are composed of molecules that depend on hydrogen bonding for their buffer solutions. Apply the concepts of structure and function, and are therefore highly sensitive to pH. Most of the reactions acid-base equilibria to in your body occur in aqueous solutions containing buffering agents.
    [Show full text]
  • Buffers and the Common-Ion Effect (Ch 16) a Buffer Works Through the Common-Ion Effect
    Buffers and the Common-ion Effect (Ch 16) A buffer works through the common-ion effect. Acetic acid in water dissociates slightly to produce some acetate ion: - + CH3COOH(aq) + H2O(l) CH3COO (aq) + H3O (aq) acetic acid acetate ion If NaCH3COO is added, it provides a source of - CH3COO ion, and the equilibrium shifts to the left. - CH3COO is common to both solutions. - The addition of CH3COO reduces the % dissociation of the acid. ©2013 McGraw-Hill Ryerson Limited 17-1 Table 17.1 The Effect of Added Acetate Ion on the Dissociation of Acetic Acid - * + [CH3COOH]init [CH3COO ]added % Dissociation [H3O ] pH 0.10 0.00 1.3 1.3x10-3 2.89 0.10 0.050 0.036 3.6x10-5 4.44 0.10 0.10 0.018 1.8x10-5 4.74 0.10 0.15 0.012 1.2x10-5 4.92 [CH COOH] * % Dissociation = 3 dissoc x 100 [CH3COOH]init ©2013 McGraw-Hill Ryerson Limited 17-2 How a Buffer Works The buffer components (HA and A-) are able to consume - + small amounts of added OH or H3O by a shift in equilibrium position. - + CH3COOH(aq) + H2O(l) CH3COO (aq) + H3O (aq) - + Added OH reacts with Added H3O reacts with - CH3COOH, causing a shift to CH3COO , causing a the right. shift to the left. The shift in equilibrium position absorbs the change in + - [H3O ] or [OH ], and the pH changes only slightly. ©2013 McGraw-Hill Ryerson Limited 17-3 Figure 17.3 How a buffer works. Buffer has more HA after Buffer has equal Buffer has more A- after + - - addition of H3O .
    [Show full text]
  • Buffer Solution Adapted from WIKI
    技 术 资 料 集 锦 NO：20140924 Buffer solution in Biology adapted from WIKI A buffer solution (more precisely, pH buffer or hydrogen ion buffer) is an aqueous solution consisting Acids and bases of a mixture of a weak acid and its conjugate base, or vice versa. Its pH changes very little when a small amount ofstrong acid or base is added to it and thus it is used to prevent changes in the pH of a solution. Buffer solutions are used as a means of keeping pH at a nearly constant value in a wide variety of chemical applications. Many life forms thrive only in a relatively small pH range so they utilize a buffer solution to maintain a constant pH. One example of a buffer solution found in nature is blood. pH Acid–base reaction Contents Acid–base titration Acid-base extraction Dissociation constant 1 Principles of buffering Acid dissociation constant 2 Applications Acid strength o 2.1 Simple buffering agents Acidity function o 2.2 "Universal" buffer mixtures Buffer solutions o 2.3 Common buffer compounds used in biology Proton affinity 3 Buffer capacity Self-ionization of water 4 Calculating buffer pH Amphoterism o 4.1 Monoprotic acids Acid types o 4.2 Polyprotic acids 5 See also Brønsted 6 References Lewis 7 External links Mineral 0510 81819585 | 189 51576701 | QQ: 2642 166682 | [email protected] 1 无锡天演生物技术有限公司 | 江苏省无锡市智慧路 33 号 7 栋 601 室 技 术 资 料 集 锦 NO：20140924 Organic Strong Superacids Principles of buffering Weak Simulated titration of an acidified solution of a weak acid (pKa = Base types 4.7) with alkali.
    [Show full text]