Redalyc.Perception of Acceleration in Motion-In-Depth with Only
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

5892 Cisco Category: Standards Track August 2010 ISSN: 2070-1721
Internet Engineering Task Force (IETF) P. Faltstrom, Ed. Request for Comments: 5892 Cisco Category: Standards Track August 2010 ISSN: 2070-1721 The Unicode Code Points and Internationalized Domain Names for Applications (IDNA) Abstract This document specifies rules for deciding whether a code point, considered in isolation or in context, is a candidate for inclusion in an Internationalized Domain Name (IDN). It is part of the specification of Internationalizing Domain Names in Applications 2008 (IDNA2008). Status of This Memo This is an Internet Standards Track document. This document is a product of the Internet Engineering Task Force (IETF). It represents the consensus of the IETF community. It has received public review and has been approved for publication by the Internet Engineering Steering Group (IESG). Further information on Internet Standards is available in Section 2 of RFC 5741. Information about the current status of this document, any errata, and how to provide feedback on it may be obtained at http://www.rfc-editor.org/info/rfc5892. Copyright Notice Copyright (c) 2010 IETF Trust and the persons identified as the document authors. All rights reserved. This document is subject to BCP 78 and the IETF Trust's Legal Provisions Relating to IETF Documents (http://trustee.ietf.org/license-info) in effect on the date of publication of this document. Please review these documents carefully, as they describe your rights and restrictions with respect to this document. Code Components extracted from this document must include Simplified BSD License text as described in Section 4.e of the Trust Legal Provisions and are provided without warranty as described in the Simplified BSD License. -

Kyrillische Schrift Für Den Computer
Hanna-Chris Gast Kyrillische Schrift für den Computer Benennung der Buchstaben, Vergleich der Transkriptionen in Bibliotheken und Standesämtern, Auflistung der Unicodes sowie Tastaturbelegung für Windows XP Inhalt Seite Vorwort ................................................................................................................................................ 2 1 Kyrillische Schriftzeichen mit Benennung................................................................................... 3 1.1 Die Buchstaben im Russischen mit Schreibschrift und Aussprache.................................. 3 1.2 Kyrillische Schriftzeichen anderer slawischer Sprachen.................................................... 9 1.3 Veraltete kyrillische Schriftzeichen .................................................................................... 10 1.4 Die gebräuchlichen Sonderzeichen ..................................................................................... 11 2 Transliterationen und Transkriptionen (Umschriften) .......................................................... 13 2.1 Begriffe zum Thema Transkription/Transliteration/Umschrift ...................................... 13 2.2 Normen und Vorschriften für Bibliotheken und Standesämter....................................... 15 2.3 Tabellarische Übersicht der Umschriften aus dem Russischen ....................................... 21 2.4 Transliterationen veralteter kyrillischer Buchstaben ....................................................... 25 2.5 Transliterationen bei anderen slawischen -

The Unicode Standard 5.1 Code Charts
Cyrillic Extended-B Range: A640–A69F The Unicode Standard, Version 5.1 This file contains an excerpt from the character code tables and list of character names for The Unicode Standard, Version 5.1. Characters in this chart that are new for The Unicode Standard, Version 5.1 are shown in conjunction with any existing characters. For ease of reference, the new characters have been highlighted in the chart grid and in the names list. This file will not be updated with errata, or when additional characters are assigned to the Unicode Standard. See http://www.unicode.org/errata/ for an up-to-date list of errata. See http://www.unicode.org/charts/ for access to a complete list of the latest character code charts. See http://www.unicode.org/charts/PDF/Unicode-5.1/ for charts showing only the characters added in Unicode 5.1. See http://www.unicode.org/Public/5.1.0/charts/ for a complete archived file of character code charts for Unicode 5.1. Disclaimer These charts are provided as the online reference to the character contents of the Unicode Standard, Version 5.1 but do not provide all the information needed to fully support individual scripts using the Unicode Standard. For a complete understanding of the use of the characters contained in this file, please consult the appropriate sections of The Unicode Standard, Version 5.0 (ISBN 0-321-48091-0), online at http://www.unicode.org/versions/Unicode5.0.0/, as well as Unicode Standard Annexes #9, #11, #14, #15, #24, #29, #31, #34, #38, #41, #42, and #44, the other Unicode Technical Reports and Standards, and the Unicode Character Database, which are available online. -

Instructions for Use
Instructions for Use Part 1 Instructions for Use – GB Manual de instrucciones – ES Bruksanvisning – SE Instructions d’utilisation – FR Οδηγίες Χρήσης - GR Gebrauchsanweisung – DE Istruzioni per l’uso – IT Instruções de utilização – PT VNG Stand Alone Unit VN415 / VO425 Valid from software version 7.07 8011826 Rev. 3 - 11/2013 Instructions for Use - GB VNG Stand Alone Unit VN415 / VO425 Valid from software version 7.00 VN415 / VO425 Instructions for Use - English Date: 2010-12-20 Page 1 Intended Use The two Interacoustics VNG systems, VN415 and VO425, are primarily intended for use in the evaluation, documentation and diagnosis of vestibular disorders. This is of particular interest to Ear, Nose and Throat specialists, to Neurology specialists, Audiology specialists and other health care professions concerned with balance assessment. The VN415 is the basic unit for peripheral vestibular testing and the VO425 is the extended system for central testing using oculomotor stimuli. Precautions WARNING indicates a hazardous situation which, if not avoided, could result in death or serious injury. CAUTION, used with the safety alert symbol, indicates a hazardous situation which, if not avoided, could result in minor or moderate injury. NOTICE is used to address practices not related to personal injury. 1. It is recommended that parts which are in direct contact with the patient (e.g. disposable goggle foam pads) should only be used with one patient, and should therefore be discarded after each session. 2. Please note that the CE Marking is only legal if this Instruction is translated into the national language of the user no later than at the delivery to him, if the national legislation demands a text in the national language according to MDD article 4.4. -

ISO/IEC International Standard 10646-1
JTC1/SC2/WG2 N3381 ISO/IEC 10646:2003/Amd.4:2008 (E) Information technology — Universal Multiple-Octet Coded Character Set (UCS) — AMENDMENT 4: Cham, Game Tiles, and other characters such as ISO/IEC 8824 and ISO/IEC 8825, the concept of Page 1, Clause 1 Scope implementation level may still be referenced as „Implementa- tion level 3‟. See annex N. In the note, update the Unicode Standard version from 5.0 to 5.1. Page 12, Sub-clause 16.1 Purpose and con- text of identification Page 1, Sub-clause 2.2 Conformance of in- formation interchange In first paragraph, remove „, the implementation level,‟. In second paragraph, remove „, and to an identified In second paragraph, remove „with an implementation implementation level chosen from clause 14‟. level‟. In fifth paragraph, remove „, the adopted implementa- Page 12, Sub-clause 16.2 Identification of tion level‟. UCS coded representation form with imple- mentation level Page 1, Sub-clause 2.3 Conformance of de- vices Rename sub-clause „Identification of UCS coded repre- sentation form‟. In second paragraph (after the note), remove „the adopted implementation level,‟. In first paragraph, remove „and an implementation level (see clause 14)‟. In fourth and fifth paragraph (b and c statements), re- move „and implementation level‟. Replace the 6-item list by the following 2-item list and note: Page 2, Clause 3 Normative references ESC 02/05 02/15 04/05 Update the reference to the Unicode Bidirectional Algo- UCS-2 rithm and the Unicode Normalization Forms as follows: ESC 02/05 02/15 04/06 Unicode Standard Annex, UAX#9, The Unicode Bidi- rectional Algorithm, Version 5.1.0, March 2008. -

Estrabismo Y Cirugía Refractiva Vol
Cabrejas L, Wakfie R, Guijarro A, Jiménez‑Alfaro I Acta Estrabológica Estrabismo y cirugía refractiva Vol. XLIX, Enero‑Junio 2020; 1: 9‑26 Monografía breve Estrabismo y cirugía refractiva Strabismus and refractive surgery Laura Cabrejas1, Rosita Lucia Wakfie Corieh2, Andrea Guijarro2, Ignacio Jiménez-Alfaro3 HU Fundación Jiménez Díaz Resumen Objetivo: Realizar una revisión bibliográfica actualizada sobre la cirugía refractiva como trata- miento para mejorar algunos tipos de estrabismo y como causa de descompensación y establecer recomendaciones para prevenirlo. Métodos: Revisión bibliográfica. Resultados: Existen pocos artículos publicados, la mayoría retrospectivos, sobre la eficacia de la cirugía refractiva en el tratamiento de la endotropia acomodativa, parcialmente acomodativa y en la exotropia. Los estudios publicados de diplopía y descompensación del estrabismo tras cirugía refractiva son escasos. Los cambios en la alineación ocular o diplopía son más frecuentes en pa- cientes con anisometropia, foria o estrabismo pre-existente y en miopía o hipermetropía elevada. Las causas principales de diplopía tras cirugía refractiva corneal son: problemas técnicos con el pro- cedimiento quirúrgico, descompensación de un estrabismo preexistente, aniseiconia y monovisión iatrogénica. En un paciente operado de catarata con diplopia la primera causa es la anestesia local, seguida de descompensación de un estrabismo preexistente, deprivación sensorial y otras patolo- gías oftalmológicas o sistémicas. En cirugía de presbicia, la monovisión inducida en pacientes con anisometropia elevada o un estrabismo preexistente puede provocar diplopia. Es fundamental determinar el riesgo previo a la cirugía, para lo cual es necesario realizar una bue- na anamnesis y exploración física y en función de ello realizar las exploraciones complementarias pertinentes. Conclusiones: La cirugía refractiva puede mejorar el ángulo de desviación de algunos tipos de estra- bismo y a la vez ser causa de diplopia y descompensación de un estrabismo previo. -

Cyrillic # Version Number
############################################################### # # TLD: xn--j1aef # Script: Cyrillic # Version Number: 1.0 # Effective Date: July 1st, 2011 # Registry: Verisign, Inc. # Address: 12061 Bluemont Way, Reston VA 20190, USA # Telephone: +1 (703) 925-6999 # Email: [email protected] # URL: http://www.verisigninc.com # ############################################################### ############################################################### # # Codepoints allowed from the Cyrillic script. # ############################################################### U+0430 # CYRILLIC SMALL LETTER A U+0431 # CYRILLIC SMALL LETTER BE U+0432 # CYRILLIC SMALL LETTER VE U+0433 # CYRILLIC SMALL LETTER GE U+0434 # CYRILLIC SMALL LETTER DE U+0435 # CYRILLIC SMALL LETTER IE U+0436 # CYRILLIC SMALL LETTER ZHE U+0437 # CYRILLIC SMALL LETTER ZE U+0438 # CYRILLIC SMALL LETTER II U+0439 # CYRILLIC SMALL LETTER SHORT II U+043A # CYRILLIC SMALL LETTER KA U+043B # CYRILLIC SMALL LETTER EL U+043C # CYRILLIC SMALL LETTER EM U+043D # CYRILLIC SMALL LETTER EN U+043E # CYRILLIC SMALL LETTER O U+043F # CYRILLIC SMALL LETTER PE U+0440 # CYRILLIC SMALL LETTER ER U+0441 # CYRILLIC SMALL LETTER ES U+0442 # CYRILLIC SMALL LETTER TE U+0443 # CYRILLIC SMALL LETTER U U+0444 # CYRILLIC SMALL LETTER EF U+0445 # CYRILLIC SMALL LETTER KHA U+0446 # CYRILLIC SMALL LETTER TSE U+0447 # CYRILLIC SMALL LETTER CHE U+0448 # CYRILLIC SMALL LETTER SHA U+0449 # CYRILLIC SMALL LETTER SHCHA U+044A # CYRILLIC SMALL LETTER HARD SIGN U+044B # CYRILLIC SMALL LETTER YERI U+044C # CYRILLIC -

Proposal to Encode Some Outstanding Early Cyrillic Characters in Unicode
ISO/IEC JTC1/SC2 WG2 N3974 Date: 2011-02-25 PONOMAR PROJECT Proposal to Encode Some Outstanding Early Cyrillic Characters in Unicode n3974 Yuri Shardt, Nikita Simmons, Aleksandr Andreev n3974 1 In old, Slavic documents that come from Eastern Europe in the centuries between A.D. 1400 and 1700, it is possible to come across various unusual characters, whose forms have not yet entered the Unicode repertoire. As well, these symbols can occasionally be found in more resent publications by those Orthodox Christians (Old Believers) that do not accept the typographic changes introduced by Patriarch Nikon in the mid-1600s. The exact forms of these symbols often vary between different places and times. In the interest of creating a standard for faithfully typesetting Slavonic manuscripts, there is a need to include these symbols in Unicode. Since these symbols are often found in Slavonic Church books, these symbols will be encoded in the “Extended Cyrillic Block B” of the Unicode standard. Characters Table 1 presents a summary of the proposed characters for encoding in Unicode: Double O and Crossed O, which are found in many early Slavonic manuscripts. The double o is used in the words двое (two), обо (both), обанадесять (twelve), and двоюнадесять (twelve), where the bold letters denote the usual placement of the proposed double o. This letter would complement the other forms of o that are already present in the Unicode standard, including the monocular o, the binocular o, the double monocular o, and the multiocular o. However, unlike the ocular o’s, which are primarily used in different words denoting eye, the double o is used in words that denote two. -

ISO/IEC International Standard 10646-1
JTC1/SC2/WG2 N3658 Proposed Draft Amendment (PDAM) 8 ISO/IEC 10646:2003/Amd.8:2009 (E) Information technology — Universal Multiple-Octet Coded Character Set (UCS) — AMENDMENT 8: Additional symbols, Bamum supplement, CJK Unified Ideographs Extension D, and other characters Page 2, Clause 3, Normative references Replace the list describing the fields of the linked con- tent (CJKU_SR.txt) and the following paragraph with Update the reference to the Unicode Bidirectional Algo- the following text: rithm and the Unicode Normalization Forms as follows: st • 1 field: BMP or SIP code point (0hhhh), Unicode Standard Annex, UAX#9, The Unicode Bidi- (2hhhh) rectional Algorithm: • 2nd field: Radical Stroke index http://www.unicode.org/reports/tr9/tr9-21.html. (d{1,3}’.d{1,2}), (Radical is one to three di- gits, optionally followed by an apostrophe for alter- Unicode Standard Annex, UAX#15, Unicode Normali- nate radical, followed by a full stop, and ending by zation Forms: one or two digits for the stroke count). http://www.unicode.org/reports/tr15/tr15-31.html. rd • 3 field: Hanzi G sources(G0-hhhh), (G1- hhhh), (G3-hhhh), (G5-hhhh), (G7- Editor’s Note: The versions for the Unicode Standard hhhh), (GS-hhhh), (G8-hhhh), (G9- Annexes mentioned above will be updated as appropri- hhhh), (GE-hhhh), (G_4K), (G_BK), ate in future phases of this amendment process. (G_BKddddd), (G_CH), (G_CY), (G_CYYddddd), (G_CHddddd), (G_FZ), Page 21, Sub-clause 23.1 Source references (G_FZddddd), (G_GHddddd), for CJK Unified Ideographs (G_GFHZBddd), (G_GJZddddd), (G_HC), -

Redalyc.A New Method to Assess Eye Dominance
Psicológica ISSN: 0211-2159 [email protected] Universitat de València España Valle-Inclán, Fernando; Blanco, Manuel J.; Soto, David; Leirós, Luz A new method to assess eye dominance Psicológica, vol. 29, núm. 1, 2008, pp. 55-64 Universitat de València Valencia, España Available in: http://www.redalyc.org/articulo.oa?id=16929103 How to cite Complete issue Scientific Information System More information about this article Network of Scientific Journals from Latin America, the Caribbean, Spain and Portugal Journal's homepage in redalyc.org Non-profit academic project, developed under the open access initiative Psicológica (2008), 29, 55-64. A new method to assess eye dominance Fernando Valle-Inclán* (1), Manuel J. Blanco (2), David Soto (2), & Luz Leirós (2) (1) University of La Coruña, Spain; (2) University of Santiago, Spain People usually show a stable preference for one of their eyes when monocular viewing is required (‘sighting dominance’) or under dichoptic stimulation conditions (‘sensory eye-dominance’). Current procedures to assess this ‘eye dominance’ are prone to error. Here we present a new method that provides a continuous measure of eye dominance and overcomes limitations of previous procedures. We presented dichoptic streams of randomly selected alphanumeric characters at rates around 5 Hz and asked observers to detect a particular character. In most subjects, the dichoptic streams of letters did not perceptually overlap, instead many participants were never aware that two letters were always presented. Interocular differences in target detection were evident in most observers, thus targets presented to one eye were always detected while targets presented to the other eye were generally missed. -
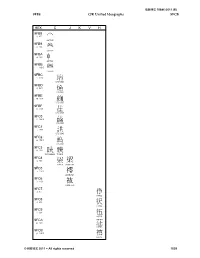
Unibook Document
ISO/IEC 10646:2011 (E) 9FB8 CJK Unified Ideographs 9FCB HEX C JKVH 9FB8 , 42.2 龸 G9-FE6D 9FB9 12.4 龹 G9-FE7E 9FBA 24.6 龺 G9-FE90 9FBB 149.12 龻 G9-FEA0 9FBC " 32.14 UTC-00836 9FBD L 86.11 UTC-00835 9FBE f 107.8 UTC-00837 9FBF 140.8 UTC-00838 9FC0 140.18 UTC-00839 9FC1 149.6 UTC-00840 9FC2 159.11 UTC-00841 9FC3 i 109.7 鿃 鿃 GKX-0809.02 T4-3946 9FC4 I 75.6 鿄 鿄 TC-4A76 JARIB-754F 9FC5 m 113.13 鿅 JARIB-7621 9FC6 m 113.4 舘 JARIB-757D 9FC7 9.6 鿇 H-87C2 9FC8 : 60.4 鿈 H-87D2 9FC9 : 60.4 鿉 H-87D6 9FCA 140.7 鿊 H-87DA 9FCB 145.12 鿋 H-87DF © ISO/IEC 2011 – All rights reserved 1029 ISO/IEC 10646:2011 (E) A000 Yi Syllables A0EF A00 A01 A02 A03 A04 A05 A06 A07 A08 A09 A0A A0B A0C A0D A0E 0 ꀀ ꀐ ꀠ ꀰ ꁀ ꁐ ꁠ ꁰ ꂀ ꂐ ꂠ ꂰ ꃀ ꃐ ꃠ A000 A010 A020 A030 A040 A050 A060 A070 A080 A090 A0A0 A0B0 A0C0 A0D0 A0E0 1 ꀁ ꀑ ꀡ ꀱ ꁁ ꁑ ꁡ ꁱ ꂁ ꂑ ꂡ ꂱ ꃁ ꃑ ꃡ A001 A011 A021 A031 A041 A051 A061 A071 A081 A091 A0A1 A0B1 A0C1 A0D1 A0E1 2 ꀂ ꀒ ꀢ ꀲ ꁂ ꁒ ꁢ ꁲ ꂂ ꂒ ꂢ ꂲ ꃂ ꃒ ꃢ A002 A012 A022 A032 A042 A052 A062 A072 A082 A092 A0A2 A0B2 A0C2 A0D2 A0E2 3 ꀃ ꀓ ꀣ ꀳ ꁃ ꁓ ꁣ ꁳ ꂃ ꂓ ꂣ ꂳ ꃃ ꃓ ꃣ A003 A013 A023 A033 A043 A053 A063 A073 A083 A093 A0A3 A0B3 A0C3 A0D3 A0E3 4 ꀄ ꀔ ꀤ ꀴ ꁄ ꁔ ꁤ ꁴ ꂄ ꂔ ꂤ ꂴ ꃄ ꃔ ꃤ A004 A014 A024 A034 A044 A054 A064 A074 A084 A094 A0A4 A0B4 A0C4 A0D4 A0E4 5 ꀅ ꀕ ꀥ ꀵ ꁅ ꁕ ꁥ ꁵ ꂅ ꂕ ꂥ ꂵ ꃅ ꃕ ꃥ A005 A015 A025 A035 A045 A055 A065 A075 A085 A095 A0A5 A0B5 A0C5 A0D5 A0E5 6 ꀆ ꀖ ꀦ ꀶ ꁆ ꁖ ꁦ ꁶ ꂆ ꂖ ꂦ ꂶ ꃆ ꃖ ꃦ A006 A016 A026 A036 A046 A056 A066 A076 A086 A096 A0A6 A0B6 A0C6 A0D6 A0E6 7 ꀇ ꀗ ꀧ ꀷ ꁇ ꁗ ꁧ ꁷ ꂇ ꂗ ꂧ ꂷ ꃇ ꃗ ꃧ A007 A017 A027 A037 A047 A057 A067 A077 A087 A097 A0A7 A0B7 A0C7 A0D7 A0E7 8 ꀈ ꀘ ꀨ -

Monoculars Monoculaires
CAUTION! Viewing the Sun may cause permanent MONOCULARS eye damage. Do not view the Sun with your monocular! INSTRUCTION MANUAL – ENGLISH PROBLEMS OR REPAIR: If warranty problems arise Thank you for purchasing a Celestron monocular. or repairs are necessary, contact the Celestron We hope it brings you many years of enjoyment. To customer service department if you live in the U.S.A. maximize your use of this monocular, please read or Canada. If you live elsewhere, please contact the these instructions carefully before using. Celestron dealer you purchased the monocular from or the Celestron distributor in your country (listings ADJUSTING FOCUS are available at www.celestron.com). To obtain a sharp view through your monocular, you WARRANTY: Your monocular has the Celestron need to adjust the focus. Rotate the focus wheel Limited Lifetime Warranty for U.S.A. and Canadian until you have a sharp image. Hint: Eyeglasses worn customers. For complete details of eligibility and for nearsightedness should be worn when using for warranty information on customers in other monoculars, as you may not be able to reach a sharp countries visit the Celestron website. focus at infinity without them. Celestron monoculars are designed and intended for SET THE RUBBER EYECUP those 13 years of age and older. To obtain the maximum field of view, twist or fold the FOR COMPLETE SPECifiCATIONS AND PRODUCT INFORMATION, rubber eyecup up if you do not wear eyeglasses and VISIT: WWW.CELESTRON.COM twist or fold it down if you do wear eyeglasses. 2835 Columbia Street • Torrance, CA 90503 U.S.A.