Development of Active Safety Systems for Rollover Prevention of All-Terrain Vehicles
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Review of Rear Axle Steering System Technology for Commercial Vehicles
연구논문 Journal of Drive and Control, Vol.17 No.4 pp.152-159 Dec. 2020 ISSN 2671-7972(print) ISSN 2671-7980(online) http://dx.doi.org/10.7839/ksfc.2020.17.4.152 A Review of Rear Axle Steering System Technology for Commercial Vehicles 하룬 아흐마드 칸1․윤소남2*․정은아2․박정우2,3․유충목4․한성민4 Haroon Ahmad Khan1, So-Nam Yun2*, Eun-A Jeong2, Jeong-Woo Park2,3, Chung-Mok Yoo4 and Sung-Min Han4 Received: 02 Nov. 2020, Revised: 23 Nov. 2020, Accepted: 28 Nov. 2020 Key Words:Rear Axle Steering, Commercial Vehicles, Centering Cylinder, Tag Axle Steering, Maneuverability Abstract: This study reviews the rear or tag axle steering system’s concepts and technology applied to commercial vehicles. Most commercial vehicles are large in size with more than two axles. Maneuvering them around tight corners, narrow roads, and spaces is a difficult job if only the front axle is steerable. Furthermore, wear and tear in tires will increase as turn angle and number of axles are increased. This problem can be solved using rear axle steering technology that is being used in commercial vehicles nowadays. Rear axle steering system technology uses a cylinder mounted on one of rear axles called a steering cylinder. Cylinder control is the primary objective of the real axle steering system. There are two types of such steering mechanisms. One uses master and slave cylinder concept while the other concept is relatively new. It goes by the name of smart axle, self-steered axle, or smart steering axle driven independently from the front wheel steering. All these different types of steering mechanisms are discussed in this study with detailed description, advantages, disadvantages, and safety considerations. -

Meritor® Tire Inflation System (Mtis) by Psi™ Including Meritor Thermalert™
MERITOR® TIRE INFLATION SYSTEM (MTIS) BY PSI™ INCLUDING MERITOR THERMALERT™ PB-9999 TABLE OF CONTENTS Control Box ............................................................................................................6 Exploded Views ......................................................................................................2 Guidelines for Specifying the Correct Kits for the Meritor Tire Infl ation System ......4 Hoses .....................................................................................................................8 Hubcaps ................................................................................................................11 Lights ....................................................................................................................6 Press Plug Kits ......................................................................................................9 Retrofi t Kit .............................................................................................................3 Through-Tees and Stators ......................................................................................8 Tools ......................................................................................................................10 Numerical Parts Listing .........................................................................................12 CONTROL BOX ASSEMBLY DUAL WHEEL END ASSEMBLY 2 U.S. 888-725-9355 Canada 800-387-3889 MERITOR TIRE INFLATION SYSTEM RETROFIT KIT Qty. Per Qty. Per Tandem Tandem -

Supercross Amateur Racing
Supercross Amateur Racing AMATEUR CLASS DESIGNATIONS Class Name Age Displacement Specifications 51cc Limited 4 - 8 0cc-51cc 2-stroke or 4-stroke 51cc Limited 4 - 6 and 51cc Limited 4 – 8 age range minicycles are both approved in this class 51cc Limited 4 - 6 0cc-51cc 2-stroke or 4-stroke Single-speed automatic. Maximum (adjusted length) wheelbase 36 inches. Maximum wheel size 10 inches. Maximum seat height 24 inches. No larger than 14 mm round intake. 51cc Limited 7 - 8 0cc-51cc 2-stroke or 4-stroke Single-speed automatic. Maximum (adjusted length) wheelbase 41 inches. Maximum wheel size 12 inches. Retrofitted 12-inch wheels are permitted on all class 2 minicycles. OEMs part must be used. No larger than 19mm round intake. Ultracross 50’s 4-8 0-51cc 2-stroke or 51cc Limited 4 - 6 and 51cc Limited 4 – 8 age range 4-stroke minicycles are both approved in this class 65cc 7 - 11 59cc-65cc 2-stroke Minimum wheel size 12 inches. Maximum front wheel 14 inches. Maximum (adjusted length) wheelbase 45 inches. Maximum wheelbase must maintain manufacturer specifications. 65cc 7 - 9 59cc-65cc 2-stroke Minimum wheel size 12 inches. Maximum front wheel 14 inches. Maximum (adjusted length) wheelbase 45 inches. Maximum wheelbase must maintain manufacturer specifications. 65cc 10 - 11 59cc-65cc 2-stroke Minimum wheel size 12 inches. Maximum front wheel 14 inches. Maximum (adjusted length) wheelbase 45 inches. Maximum wheelbase must maintain manufacturer specifications. 85cc 9 - 12 79cc-85cc 2-stroke Maximum front wheel 17” Minimum rear wheel 12” Maximum rear wheel 16” Maximum wheel base 51” Mini Senior 12 - 15 79cc-85cc 2-stroke or 75-150cc 4-stroke Maximum front wheel17” Minimum rear wheel 12” Maximum rear wheel 16” Maximum wheel base 51” Supermini 1 9 - 15 79cc-112cc 2-stroke or 75cc-150cc 4-stroke Maximum front wheel 19” Maximum rear wheel 16” Maximum wheel base 52” *Competitors 9 thru 11 yrs of age are only allowed to use a 79cc - 85cc 2-stroke minicycle if competing in this class. -
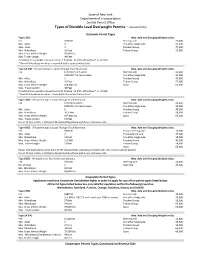
Types of Divisible Load Overweight Permits – Perm 69 (07/09)
State of New York Department of Transportation Central Permit Office Types of Divisible Load Overweight Permits – Perm 69 (07/09) Statewide Permit Types Type 1 (F1) Max. Axle and Grouping Weights in Lbs. Fee $360.00 Steering axle 22,400 Min. Axles 3 Any other Single axle 25,000 Max. Axles 4 Tandem Group 47,000 Min. Wheelbase 16 Feet Tridem Group 57,000 Max. Gross Vehicle Weight 97,400 Lbs. Max. Trailer Length 48 Feet Permitted Gross weight is based on the F1 formula : (1,250 x Wheelbase* ) + 42,500 * Overall Wheelbase in inches is rounded to the nearest whole foot. Type 1A (F1) - This permit type is Large Through Truck Restricted. Max. Axle and Grouping Weights in Lbs. Fee $750.00 (5 or 6 axles) Steering axle 22,400 $900.00 (7 or more axles) Any other Single axle 25,000 Min. Axles 5 Tandem Group 47,000 Min. Wheelbase 16 Feet Tridem Group 57,000 Max. Gross Vehicle Weight 102,000 Lbs. Quad 62,000 Max. Trailer Length 48 Feet Permitted Gross weight is based on the F1 formula : (1,250 x Wheelbase* ) + 42,500 * Overall Wheelbase in inches is rounded to the nearest whole foot. Type 7 (F2) - This permit type is Large Through Truck Restricted. Max. Axle and Grouping Weights in Lbs. Fee $750.00 (6 axles) Steering axle 22,400 $900.00 (7 or more axles) Any other Single axle 25,000 Min. Axles 6 Tandem Group 48,000 Min. Wheelbase 36 ½ feet Tridem Group 58,000 Max. Gross Vehicle Weight 107,000 Lbs. -

Bendix ABS-6 Advanced with ESP Stability System
Bendix® ABS-6 Advanced with ESP® Stability System Frequently Asked Questions to Help You Make an Intelligent Investment in Stability Contents: Key FAQs (Start here!)………….. Pg. 2 Stability Definitions …………….. Pg. 6 System Comparison ……………. Pg. 7 Function/Performance ………….. Pg. 9 Value ………………………………. Pg. 12 Availability/Applications ……….. Pg. 14 Vehicle System Integration …….. Pg. 16 Safety ………………………………. Pg. 17 Take the Next Step ………………. Pg. 18 Please note: This document is designed to assist you in the stability system decision process, not to serve as a performance guarantee. No system will prevent 100% of the incidents you may experience. This information is subject to change without notice © 2007 Bendix Commercial Vehicle Systems LLC, a member of the Knorr-Bremse Group. All Rights Reserved. 03/07 1 Key FAQs What is roll stability? Roll stability counteracts the tendency of a vehicle, or vehicle combination, to tip over while changing direction (typically while turning). The lateral (side) acceleration creates a force at the center of gravity (CG), “pushing” the truck/tractor-trailer horizontally. The friction between the tires and the road opposes that force. If the lateral force is high enough, one side of the vehicle may begin to lift off the ground potentially causing the vehicle to roll over. Factors influencing the sensitivity of a vehicle to lateral forces include: the load CG height, load offset, road adhesion, suspension stiffness, frame stiffness and track width of vehicle. What is yaw stability? Yaw stability counteracts the tendency of a vehicle to spin about its vertical axis. During operation, if the friction between the road surface and the tractor’s tires is not sufficient to oppose lateral (side) forces, one or more of the tires can slide, causing the truck/tractor to spin. -

2021 Ram 1500 Classic
SEDANS MINIVANS/CROSSOVERS SPORT UTILITY TRUCKS/COMMERCIAL LAW ENFORCEMENT 2021 RAM 1500 CLASSIC SELECT STANDARD FEATURES 3.6L Pentastar® V6 / 850RE 8-speed Automatic Air Conditioning — Manual Alternator — 160-amp Axle — 3.21 ratio Battery — 730-amp Cluster — Instrument, with 3.5-inch display screen for Driver Information Display Fuel Tank — 26-gallon Headlamps — Automatic quad-lens halogen with incandescent taillamps Mirrors — 6 x 9-inch Seats — 40/20/40 split-bench front seat with folding front armrest/cup holder, floor-mounted storage tray on Crew Cab (Quad Cab® and Crew Cab models include folding rear bench seat) Shock Absorbers — Heavy-duty, front and rear Spare Tire — Full-size Stabilizer Bar — Front and rear Steering — Electronic, rack and pinion Storage — Front, behind the seats (Regular Cab only) Properly secure all cargo. — Rear, in-floor bins, two with removable liners (Crew Cab only) — Rear, underseat compartment (Quad Cab and Crew Cab models only) Styled Steel Wheels — 17 x 7-inch Suspension — Front, upper and lower A-arms, coil springs, twin-tube shocks — Rear, five-link, coil springs, twin-tube shocks Tires — P265 / 70R17 BSW A/S Transfer Case — Electronic part-time (4x4 models only) Windows — Manual (Regular Cab only) — Power, front and rear with driver’s one-touch up/down (Quad Cab and Crew Cab models only) SAFETY & SECURITY Air Bags(2) — Advanced multistage front — Supplemental side-curtain — Supplemental front-seat side-mounted Brakes — Power-assisted four-wheel antilock disc Electronic Stability Control(3) — Includes Four-wheel Antilock Brake System, Brake Assist, All-Speed Traction Control, Rain Brake Support, Ready Alert Braking, Electronic Roll Mitigation, Hill Start Assist and Trailer Sway Damping(3) ParkView® Rear Back-Up Camera(22) ENGINES HORSEPOWER(17) TORQUE(17) Properly secure all cargo. -

1976 Technical Documentation Locomotive Truck Hunting M.Pdf
TECHNICAL DOCUMENTATION LOCOMOTIVE TRUCK HUNTING MODEL V. K. Garg OHO G. C. Martin P. W. Hartmann J. G. Tolomei mnnnn irnational Government-Industry 04 - Locomotives ch Program on Track Train Dynamics R-219 TE C H N IC A L DOCUMENTATION rnn nnn LOCOMOTIVE TRUCK HUNTING MODEL V. K. Garg G. C. Martin P. W. Hartmann a a J. G. Tolomei dD 11 TT|[inr i3^1 i i H§ic§ An International Government-Industry Research Program on Track Train Dynamics Chairman L. A. Peterson J. L. Cann Director Vice President Office of Rail Safety Research Steering Operation and Maintenance Federal Railroad Administration Canadian National Railways G. E. Reed Vice Chairman Director Committee W. J. Harris, Jr. Railroad Sales Vice President AMCAR Division Research and Test Department ACF Industries Association of American Railroads D. V. Sartore or the E. F. Lind Chief Engineer Design Project Director-Phase I Burlington Northern, Inc. Track Train Dynamics Southern Pacific Transportation Co. P. S. Settle Tack Tain President M. D. Armstrong Railway Maintenance Corporation Chairman Transportation Development Agency W. W. Simpson Dynamics Canadian Ministry of Transport Vice President Engineering W. S. Autrey Southern Railway System Chief Engineer Atchison, Topeka & Santa Fe Railway Co. W. S. Smith Vice President and M. W. Beilis Director of Transportation Manager General Mills, Inc. Locomotive Engineering General Electric Company J. B. Stauffer Director M. Ephraim Transportation Test Center Chief Engineer Federal Railroad Administration Electro Motive Division General Motors Corporation R. D. Spence (Chairman) J. G. German President Vice President ConRail Engineering Missouri Pacific Co. L. S. Crane (Chairman) President and Chief W. -

Specifiers & Installers Guide to TORSION BAR APPLICATIONS
Specifiers & Installers Guide To TORSION BAR APPLICATIONS WELCOME Thank you for specifying Sauber Torsion Bars. By choosing us as your stability partner, you derive the following benefits: * Improved Stability * Stability is safety, and safety is our first concern. A Sauber Torsion Bar can eliminate unwanted counterweight, offering your users an extra safety margin. Because Sauber bars don't rigidize the chassis frame, they always provide a smooth, quiet ride. * Long Life * Premium bronze and galvanized components. Bushings guaranteed and replaced as/if needed for 10 years. 10 Year parts coverage when inspected at no greater than four month intervals. * Excellent Documentation * Our comprehensive applications charts, installation instructions and detailed drawings provide the vital information you and your installers need in an organized format. * Superior Support * Toll-free phone and fax service from anywhere in North America provides easy access to the resources of our organization through your personal company representative. * Lower Life Cycle Costs * Since it takes less time to mount our bar, its installed cost can actually be less than other alternatives. Sauber Torsion Bars are designed and built to last as long as your chassis. * Extensive Inventory * Our inventory power puts our bar on the floor just when you want it. Your production schedule can't wait on your suppliers, and with us as your partner, it won't. * More Choices * Underframe or overframe, nobody provides more installation options than we do. More choices mean a better -

Road Map for the Future Making the Case for Full-Stability
ROAD MAP FOR THE FUTURE MAKING THE CASE FOR FULL-STABILITY Bendix Commercial Vehicle Systems LLC 901 Cleveland Street • Elyria, Ohio 44035 1-800-247-2725 • www.bendix.com/abs6 road map for the future : making the case for full-stability TABLE OF CONTENTS 1 : Important Terms ............................................... 3-4 2 : Executive Summary ............................................. 5-7 3 : Understanding Stability Systems .................................. 8-12 4 : The Difference Between Roll-Only and Full-Stability Systems ...........13-23 5 : Stability for Straight Trucks/Vocational Vehicles ......................24-26 6 : Why Data Supports Full-Stability Systems ..........................27-30 7 : The Safety ROI of Stability Systems ................................31-33 8 : Recognizing the Limitations of Stability Systems ......................34-37 9 : Stability System Maintenance .....................................38-40 10 : Stability as the Foundation for Future Technologies ...................41-42 11 : Conclusion .................................................. 43-44 12 : Appendix A: Analysis of the “Large Truck Crash Causation Study” ..... 45-46 13 : About the Authors ................................................47 road map for the future : making the case for full-stability 1 : 1 2 IMPORtant teRMS Directional Instability Before delving into information about the The loss of the vehicle’s ability to follow the driver’s steering, technological differences acceleration or braking input. between commercial vehicle -

Eaton® Repair Information
® Eaton October, 1991 Hydrostatic Transaxle Repair Information A 751, 851, 771, and 781 Transaxle 1 The following repair information applies to mance. Work in a clean area. After disassem- the Eaton 751, 851,771, and 781 series hydro- bly, wash all parts with clean solvent and blow static transaxles. the parts dry with air. Inspect all mating sur- faces. Replace any damaged parts that could cause internal leakage. Do not use grit paper, files or grinders on finished parts. Note: Whenever a transaxle is disassembled, our recommendation is to replace all seals. Lubricate the new seals with petroleum jelly before installation. Use only clean, recom- mended hydraulic fluid on the finished sur- faces at reassembly. Part Number, Date of Assembly, and Input Rotation Stamped on this Surface 6 The following tools are required for disas- Assembly Date of Part Number Input Rotation Build Code sembly and reassembly of the transaxle. (CW or CCW) • 3/8 in. Socket or End Wrench Customer • 1 in. Socket or End Wrench Part Number XXX-XXX XXX XXXXXX Factory ( if Required ) XXXXXX XX/XX/XX 11 Rebuild • Ratchet Wrench Code • Torque Wrench 300 lb-in [34 Nm] Original Build Factory Rebuild ( example - 010191 ) ( example - 01/01/91 11 ) • 5/32 Hex Wrench 01 01 91 01 01 91 11 • Small screwdriver (4 in [102 mm] to 6 in. Year Number of [150 mm] long) Day Year Times Rebuilt (2) • No. 5 or 7 Internal Retaining Ring Pliers Month Day Month • No. 4 or 5 External Retaining Ring Pliers • 6 in. [150 mm] or 8 In. -

MICHELIN® Truck Tire Reference Chart
MICHELI N® Truck Tire Reference Chart January 2012 MICHELIN ® TRUCK TIRE REFERENCE CHART STEER / ALL-POSITION TIRES (3) XZA3 ®+ EVERTREAD ™ XZA ® (365/70R22.5) XZA2 ® ENERGY • Ultra-fuel-efficient tire (1) that delivers • Advanced Technology ™ compounding • Optimized channel design allows for long our longest mileage in line haul steer offers excellent fuel economy (1) tread life and minimized irregular wear applications • Engineered for irregular wear resistance • Low rolling resistance compounds for fuel • Dual Compound Tread delivers more • Over 7,000 trapezoidal micro sipes on economy (1) in highway service mileage without compromising ultra- groove edges help break water surface • Optimized for steer axle service fuel-efficiency and retreadability tension to promote traction on wet and • Directional tread with enhanced shoulder slippery road surfaces rib designed to deliver even wear to the end • Original shoulder groove design offers • 3-Retread Limited Warranty (2) enhanced resistance to uneven shoulder wear LH R O/O U LH R O/O U LH R O/O U 275/80R22.5 Tread Depth 365/70R22.5 Tread Depth 315/80R22.5 Tread Depth MICHELIN ® XZA3 ®+ EVERTREAD ™ 19 MICHELIN ® XZA ® 19 MICHELIN ® XZA2 ® ENERGY 16 Goodyear ® G395 LHS Fuel Max 18 Goodyear ® N/A Goodyear ® G291 18 Bridgestone ® R287A 16 Bridgestone ® N/A Bridgestone ® R294 19 XZA ®-1+ XZA ®1(3) XZE ® • Decoupling groove built for resistance to • Optimized for all-position heavy axle • Solid shoulders to help resist scrub irregular wear loads • Curb guards on sidewalls • Optimized for steer -

Design of Automotive X-By-Wire Systems Cédric Wilwert, Nicolas Navet, Ye-Qiong Song, Françoise Simonot-Lion
Design of automotive X-by-Wire systems Cédric Wilwert, Nicolas Navet, Ye-Qiong Song, Françoise Simonot-Lion To cite this version: Cédric Wilwert, Nicolas Navet, Ye-Qiong Song, Françoise Simonot-Lion. Design of automotive X-by- Wire systems. Richard Zurawski. The Industrial Communication Technology Handbook, CRC Press, 2005, 0849330777. inria-00000562 HAL Id: inria-00000562 https://hal.inria.fr/inria-00000562 Submitted on 27 Aug 2007 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Design of automotive X-by-Wire systems Cédric Wilwert PSA Peugeot - Citroën 92000 La Garenne Colombe - France Fax: +33 3 83 58 17 01 Phone: +33 3 83 58 17 17 [email protected] Nicolas Navet LORIA UMR 7503 – INRIA Campus Scientifique - BP 239 - 54506 VANDOEUVRE-lès-NANCY CEDEX Fax: +33 3 83 58 17 01 Phone : +33 3 83 58 17 61 [email protected] Ye Qiong Song LORIA UMR 7503 – Université Henri Poincaré Nancy I Campus Scientifique - BP 239 - 54506 VANDOEUVRE-lès-NANCY CEDEX Fax: +33 3 83 58 17 01 Phone : +33 3 83 58 17 64 [email protected] Françoise Simonot-Lion LORIA UMR 7503 – Institut National Polytechnique de Lorraine Campus Scientifique - BP 239 - 54506 VANDOEUVRE-lès-NANCY CEDEX Fax: +33 3 83 27 83 19 Phone : +33 3 83 58 17 62 [email protected] CONTENTS Design of automotive X-by-Wire systems ......................................................................................................