Notes on Cinemetric Data Analysis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Cutting Patterns in DW Griffith's Biographs
Cutting patterns in D.W. Griffith’s Biographs: An experimental statistical study Mike Baxter, 16 Lady Bay Road, West Bridgford, Nottingham, NG2 5BJ, U.K. (e-mail: [email protected]) 1 Introduction A number of recent studies have examined statistical methods for investigating cutting patterns within films, for the purposes of comparing patterns across films and/or for summarising ‘average’ patterns in a body of films. The present paper investigates how different ideas that have been proposed might be combined to identify subsets of similarly constructed films (i.e. exhibiting comparable cutting structures) within a larger body. The ideas explored are illustrated using a sample of 62 D.W Griffith Biograph one-reelers from the years 1909–1913. Yuri Tsivian has suggested that ‘all films are different as far as their SL struc- tures; yet some are less different than others’. Barry Salt, with specific reference to the question of whether or not Griffith’s Biographs ‘have the same large scale variations in their shot lengths along the length of the film’ says the ‘answer to this is quite clearly, no’. This judgment is based on smooths of the data using seventh degree trendlines and the observation that these ‘are nearly all quite different one from another, and too varied to allow any grouping that could be matched against, say, genre’1. While the basis for Salt’s view is clear Tsivian’s apparently oppos- ing position that some films are ‘less different than others’ seems to me to be a reasonably incontestable sentiment. It depends on how much you are prepared to simplify structure by smoothing in order to effect comparisons. -

German Operetta on Broadway and in the West End, 1900–1940
Downloaded from https://www.cambridge.org/core. IP address: 170.106.202.58, on 26 Sep 2021 at 08:28:39, subject to the Cambridge Core terms of use, available at https://www.cambridge.org/core/terms. https://www.cambridge.org/core/product/2CC6B5497775D1B3DC60C36C9801E6B4 Downloaded from https://www.cambridge.org/core. IP address: 170.106.202.58, on 26 Sep 2021 at 08:28:39, subject to the Cambridge Core terms of use, available at https://www.cambridge.org/core/terms. https://www.cambridge.org/core/product/2CC6B5497775D1B3DC60C36C9801E6B4 German Operetta on Broadway and in the West End, 1900–1940 Academic attention has focused on America’sinfluence on European stage works, and yet dozens of operettas from Austria and Germany were produced on Broadway and in the West End, and their impact on the musical life of the early twentieth century is undeniable. In this ground-breaking book, Derek B. Scott examines the cultural transfer of operetta from the German stage to Britain and the USA and offers a historical and critical survey of these operettas and their music. In the period 1900–1940, over sixty operettas were produced in the West End, and over seventy on Broadway. A study of these stage works is important for the light they shine on a variety of social topics of the period – from modernity and gender relations to new technology and new media – and these are investigated in the individual chapters. This book is also available as Open Access on Cambridge Core at doi.org/10.1017/9781108614306. derek b. scott is Professor of Critical Musicology at the University of Leeds. -

Papéis Normativos E Práticas Sociais
Agnes Ayres (1898-194): Rodolfo Valentino e Agnes Ayres em “The Sheik” (1921) The Donovan Affair (1929) The Affairs of Anatol (1921) The Rubaiyat of a Scotch Highball Broken Hearted (1929) Cappy Ricks (1921) (1918) Bye, Bye, Buddy (1929) Too Much Speed (1921) Their Godson (1918) Into the Night (1928) The Love Special (1921) Sweets of the Sour (1918) The Lady of Victories (1928) Forbidden Fruit (1921) Coals for the Fire (1918) Eve's Love Letters (1927) The Furnace (1920) Their Anniversary Feast (1918) The Son of the Sheik (1926) Held by the Enemy (1920) A Four Cornered Triangle (1918) Morals for Men (1925) Go and Get It (1920) Seeking an Oversoul (1918) The Awful Truth (1925) The Inner Voice (1920) A Little Ouija Work (1918) Her Market Value (1925) A Modern Salome (1920) The Purple Dress (1918) Tomorrow's Love (1925) The Ghost of a Chance (1919) His Wife's Hero (1917) Worldly Goods (1924) Sacred Silence (1919) His Wife Got All the Credit (1917) The Story Without a Name (1924) The Gamblers (1919) He Had to Camouflage (1917) Detained (1924) In Honor's Web (1919) Paging Page Two (1917) The Guilty One (1924) The Buried Treasure (1919) A Family Flivver (1917) Bluff (1924) The Guardian of the Accolade (1919) The Renaissance at Charleroi (1917) When a Girl Loves (1924) A Stitch in Time (1919) The Bottom of the Well (1917) Don't Call It Love (1923) Shocks of Doom (1919) The Furnished Room (1917) The Ten Commandments (1923) The Girl Problem (1919) The Defeat of the City (1917) The Marriage Maker (1923) Transients in Arcadia (1918) Richard the Brazen (1917) Racing Hearts (1923) A Bird of Bagdad (1918) The Dazzling Miss Davison (1917) The Heart Raider (1923) Springtime à la Carte (1918) The Mirror (1917) A Daughter of Luxury (1922) Mammon and the Archer (1918) Hedda Gabler (1917) Clarence (1922) One Thousand Dollars (1918) The Debt (1917) Borderland (1922) The Girl and the Graft (1918) Mrs. -

Teacher Support Materials to Use With
Teacher support materials to use with Brief Plot Summary Discussion Questions Historical Drawings and Photos for Discussion Detailed Plot Summary Historical Background What Did You Read? – Form Book Report – Form Word Play Activity Fill in the Blanks Review Activity Brief Plot Summary For Gold and Blood tells the story of two Chinese brothers, Soo and Ping Lee, who, like many Chinese immigrants, leave their home in China to go to California in 1851. They hope to strike it rich in the Gold Rush and send money back to their family. In the gold fields, they make a big strike but are cheated out of it. After 12 years of prospecting, they split up. Soo joins the Chinese workers who build the Central Pacific Railroad, while Ping opens a laundry in San Francisco. With little to show for his work, Soo also goes to San Francisco. Both men face prejudice and violence. In time they join rival factions in the community of Chinatown, Ping with one of the Chinese Six Families and Soo with a secret, illegal tong. The story ends after the 1906 earthquake. This dramatic historical novel portrays the complicated lives of typical immigrants from China and many other countries. Think about it For Gold and Blood Discussion Questions Chapter 1 Leaving Home 1. If you were Ping, would you leave home for the possibility of finding gold so far away? 2. The brothers had to pay money to get out of the country. Does that happen now? 3. Do you think it’s possible to get rich fast without breaking the law? 4. -

Orchestral Music
Orchestral Music No. Composer Arranger Short Title Grade Class Scoring 3052 Thomas C Rudolf C xmas string 3 vlc 3053 Thomas C French Carol C xmas string 3 vlc 3057 Thomas C We Wish You A Merry Christmas C xmas string 4 vlc 2244 Abba Waignein Forever Abba Gold C wind wind/brass/flexible 4 2791 Abba Waignein Forever Abba Gold C wind wind/flexible/brass 4 1950 Abbe, Donald Ten Elementary Percussions D perc perc 3 1798 Abel A London Bridge Sextet C perc perc 5 1801 Abel A Holiday Special Sextet C perc perc 6 2786 Abreu et al Rapp W Tico Tico (Tico NoFuba) B perc perc 6 4019 Adkins & Epworth Moore Skyfall orch strings 199 Adley/Frazer Stone D Encounter B perc perc 8 1368 Adley/Frazer Sounds Latin C perc perc 8 1441 Adley/Frazer Frere Jacques D perc perc 4-8 2478 Albeniz Arnold M Tango in D C orch orch 3077 Albeniz Lewin G Malaguena B wind 4 sax 272 Albinoni Polnauer Sonata for String Orchestra Op6 No2 A orch strings 355 Albinoni Kneusslin Concerto Dmin Op9 No2 Oboe & Strings B orch strings ob 1195 Albinoni Adagio in Gmin Organ & Strings B orch strings organ 1286 Albinoni Concerto in Bb Op7 No3 Oboe & Strings B orch strings ob 1778 Albinoni Wade D Concerto in Emin for Strings & cembalo B orch strings cem 1782 Albinoni Wade D Grave & Allegro B orch strings 2043 Albinoni Polnauer Sonata for String Orchestra Op6 No2 B orch strings 1553 Albright Take That A perc perc 4 1516 Alfieri Fanfare: 6 Tambourines B perc perc 6 1160 Alford Evans Colonel Bogey C orch flexible 288 Alfven Hare Themes 'Swedish Rhapsody' D orch flexible 3063 Alfven Hare Swedish -

"Our Own Flesh and Blood?": Delaware Indians and Moravians in the Eighteenth-Century Ohio Country
Graduate Theses, Dissertations, and Problem Reports 2017 "Our Own Flesh and Blood?": Delaware Indians and Moravians in the Eighteenth-Century Ohio Country. Jennifer L. Miller Follow this and additional works at: https://researchrepository.wvu.edu/etd Recommended Citation Miller, Jennifer L., ""Our Own Flesh and Blood?": Delaware Indians and Moravians in the Eighteenth- Century Ohio Country." (2017). Graduate Theses, Dissertations, and Problem Reports. 8183. https://researchrepository.wvu.edu/etd/8183 This Dissertation is protected by copyright and/or related rights. It has been brought to you by the The Research Repository @ WVU with permission from the rights-holder(s). You are free to use this Dissertation in any way that is permitted by the copyright and related rights legislation that applies to your use. For other uses you must obtain permission from the rights-holder(s) directly, unless additional rights are indicated by a Creative Commons license in the record and/ or on the work itself. This Dissertation has been accepted for inclusion in WVU Graduate Theses, Dissertations, and Problem Reports collection by an authorized administrator of The Research Repository @ WVU. For more information, please contact [email protected]. “Our Own Flesh and Blood?”: Delaware Indians and Moravians in the Eighteenth-Century Ohio Country Jennifer L. Miller Dissertation submitted to the Eberly College of Arts and Sciences At West Virginia University in partial fulfillment of the requirements for the degree of Doctor of Philosophy in History Tyler Boulware, Ph.D., chair Melissa Bingmann, Ph.D. Joseph Hodge, Ph.D. Brian Luskey, Ph.D. Rachel Wheeler, Ph.D. Department of History Morgantown, West Virginia 2017 Keywords: Moravians, Delaware Indians, Ohio Country, Pennsylvania, Seven Years’ War, American Revolution, Bethlehem, Gnadenhütten, Schoenbrunn Copyright 2017 Jennifer L. -

D.W. Griffith
LIGHTS, CAMERA, FILM LITERACY! Framing, Composition, and Distance: Early Narrative Films by D.W. Griffith SOME POSSIBLE ANSWERS TITLE FRAMING COMPOSITION CAMERA DISTANCE 5 shots: water centered: Cart moves lower right to upper left: Long Shots 1) land top and bottom Barrel drops in center 1) Cart close to camera at edge of water The Adventures of Dollie 2) land at top Barrel moves to lower right and moves away from. (1908) 3) waterfall left to right Barrel downward and toward viewer 2) Barrel comes toward camera. land at top/eye slightly above Barrel downward and toward viewer 3) Barrel comes toward camera. 8:10–10:10 4) land on right and left Barrel from upper left to lower right 4) Barrel comes toward camera. 5) land upper right 5) Barrel comes toward camera. WATER ADDS MOVEMENT! Door on left Man standing Medium shot Window on right Girl seated (later stands) The Girl and Her Trust No floor nor ceiling shown Window blind and hanging papers add (1910) Clock pendulum centered on back balance to the differing heights wall… ADDS MOVEMENT! 1:15–1:50 Inner room: Inner room: Medium shots Part of a table on the left Butler stands at center between two The Burglar’s Dilemma Column at back left wall brothers. (1911) Right wall with door and mid-height Popular brother takes up more screen curio cabinet…sculpture on top space…heavier, holds open newspaper, Tall cabinet centered at back wall sits more toward the center 1:34-2:20 No floor nor ceiling shown Tormented one is slender and holds a Outer room: small paperback book or script and sits Door on left close to the right Partial back wall with small table, The women are in the center and turn and a painting above. -

The Bates Student
Bates College SCARAB The aB tes Student Archives and Special Collections 5-1911 The aB tes Student - volume 39 number 05 - May 1911 Bates College Follow this and additional works at: http://scarab.bates.edu/bates_student Recommended Citation Bates College, "The aB tes Student - volume 39 number 05 - May 1911" (1911). The Bates Student. 1826. http://scarab.bates.edu/bates_student/1826 This Newspaper is brought to you for free and open access by the Archives and Special Collections at SCARAB. It has been accepted for inclusion in The aB tes Student by an authorized administrator of SCARAB. For more information, please contact [email protected]. w TM STVMNT MAY 1911„ ■■ • CONTENTS A My Mother Walter James Graham, ' 11 The Cynic of Parker Hall Alton Rocs Hodgkins, '11 145 Two Flag* Irving Hill Blake, '11 149 Dante Vincent Gatto, '14 150 Editorial 155 Local 159 Athletic* 163 Alumni 169 Exchanges • ' .'.:■■ 175 Spice Box 177 - s ■BMB BUSINESS DIRECTORY THE GLOBE STEAM LAUNDRY, 26-36 Temple Street, PORTLAND MUSIC HALL A. P. BIBBER, Manager The Home of High-Class Vaudeville Prices, 5 and 10 Cents Reserved Seats at Night, 15 Cents MOTION PICTURES CALL AT THB STUDIO of FLAGG ©• PLUMMER For the most up-to-date work in Photography OPPOSITE MUSIC HALL BATES FIRST-GLASS WORK STATIONERY AT In Box and Tablet Form Engraving for Commencement Merrill k Butter's A SPECIALTY % Berry Paper Company 189 Main Street, Cor. Park 49 Lisbon Street, LEWISTON BENJAMIN CLOTHES Always attract attention among the college fellows, because they have the snap and style that other lines do not have You can buy these clothes for the next thirty days at a reduction of over 20 per cent L. -
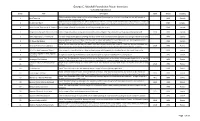
GCMF Poster Inventory
George C. Marshall Foundation Poster Inventory Compiled August 2011 ID No. Title Description Date Period Country A black and white image except for the yellow background. A standing man in a suit is reaching into his right pocket to 1 Back Them Up WWI Canada contribute to the Canadian war effort. A black and white image except for yellow background. There is a smiling soldier in the foreground pointing horizontally to 4 It's Men We Want WWI Canada the right. In the background there is a column of soldiers march in the direction indicated by the foreground soldier's arm. 6 Souscrivez à L'Emprunt de la "Victoire" A color image of a wide-eyed soldier in uniform pointing at the viewer. WWI Canada 2 Bring Him Home with the Victory Loan A color image of a soldier sitting with his gun in his arms and gear. The ocean and two ships are in the background. 1918 WWI Canada 3 Votre Argent plus 5 1/2 d'interet This color image shows gold coins falling into open hands from a Canadian bond against a blue background and red frame. WWI Canada A young blonde girl with a red bow in her hair with a concerned look on her face. Next to her are building blocks which 5 Oh Please Do! Daddy WWI Canada spell out "Buy me a Victory Bond" . There is a gray background against the color image. Poster Text: In memory of the Belgian soldiers who died for their country-The Union of France for Belgium and Allied and 7 Union de France Pour La Belqiue 1916 WWI France Friendly Countries- in the Church of St. -

The Silent Film Project
The Silent Film Project Films that have completed scanning – Significant titles in bold: May 1, 2018 TITLE YEAR STUDIO DIRECTOR STAR 1. [1934 Walt Disney Promo] 1934 Disney 2. 13 Washington Square 1928 Universal Melville W. Brown Alice Joyce 3. Adventures of Bill and [1921] Pathegram Robert N. Bradbury Bob Steele Bob, The (Skunk, The) 4. African Dreams [1922] 5. After the Storm (Poetic [1935] William Pizor Edgar Guest, Gems) Al Shayne 6. Agent (AKA The Yellow 1922 Vitagraph Larry Semon Larry Semon Fear), The 7. Aladdin And The 1917 Fox Film C. M. Franklin Francis Wonderful Lamp Carpenter 8. Alexandria 1921 Burton Holmes Burton Holmes 9. An Evening With Edgar A. [1938] Jam Handy Louis Marlowe Edgar A. Guest Guest 10. Animals of the Cat Tribe 1932 Eastman Teaching 11. Arizona Cyclone, The 1934 Imperial Prod. Robert E. Tansey Wally Wales 12. Aryan, The 1916 Triangle William S. Hart William S. Hart 13. At First Sight 1924 Hal Roach J A. Howe Charley Chase 14. Auntie's Portrait 1914 Vitagraph George D. Baker Ethel Lee 15. Autumn (nature film) 1922 16. Babies Prohibited 1913 Thanhouser Lila Chester 17. Barbed Wire 1927 Paramount Rowland V. Lee Pola Negri 18. Barnyard Cavalier 1922 Christie Bobby Vernon 19. Barnyard Wedding [1920] Hal Roach 20. Battle of the Century 1927 Hal Roach Clyde Bruckman Oliver Hardy, Stan Laurel 21. A Beast at Bay 1912 Biograph D.W. Griffith Mary Pickford 22. Bebe Daniels & Ben Lyon 1931- Bebe Daniels, home movies 1935 Ben Lyon 23. Bell Boy 13 1923 Thomas Ince William Seiter Douglas Maclean 24. -

Operetta After the Habsburg Empire by Ulrike Petersen a Dissertation
Operetta after the Habsburg Empire by Ulrike Petersen A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Music in the Graduate Division of the University of California, Berkeley Committee in Charge: Professor Richard Taruskin, Chair Professor Mary Ann Smart Professor Elaine Tennant Spring 2013 © 2013 Ulrike Petersen All Rights Reserved Abstract Operetta after the Habsburg Empire by Ulrike Petersen Doctor of Philosophy in Music University of California, Berkeley Professor Richard Taruskin, Chair This thesis discusses the political, social, and cultural impact of operetta in Vienna after the collapse of the Habsburg Empire. As an alternative to the prevailing literature, which has approached this form of musical theater mostly through broad surveys and detailed studies of a handful of well‐known masterpieces, my dissertation presents a montage of loosely connected, previously unconsidered case studies. Each chapter examines one or two highly significant, but radically unfamiliar, moments in the history of operetta during Austria’s five successive political eras in the first half of the twentieth century. Exploring operetta’s importance for the image of Vienna, these vignettes aim to supply new glimpses not only of a seemingly obsolete art form but also of the urban and cultural life of which it was a part. My stories evolve around the following works: Der Millionenonkel (1913), Austria’s first feature‐length motion picture, a collage of the most successful stage roles of a celebrated -

Hitchcock's Music
HITCHCOCK’S MUSIC HITCHCOCK’S MUSIC jack sullivan yale university pr ess / new haven and london Copyright © 2006 by Yale University. All rights reserved. This book may not be reproduced, in whole or in part, including illustrations, in any form (beyond that copying permitted by Sections 107 and 108 of the U.S. Copyright Law and except by reviewers for the public press),without written permission from the publishers. Designed by Mary Valencia. Set in Minion type by The Composing Room of Michigan, Inc. Printed in the United States of America by Sheridan Books. Library of Congress Cataloging-in-Publication Data Sullivan, Jack, 1946– Hitchcock’s music / Jack Sullivan. p. cm. Includes bibliographical references and index. ISBN-13: 978-0-300-11050-0 (cloth : alk. paper) ISBN-10: 0-300-11050-2 1. Motion picture music—History and criticism. 2. Television music—History and criticism. 3. Hitchcock, Alfred, 1899–1980—Criticism and interpretation. I. Title. ML2075.S89 2006 781.5Ј42—dc22 2006010348 A catalogue record for this book is available from the British Library. The paper in this book meets the guidelines for permanence and durability of the Committee on Production Guidelines for Book Longevity of the Council on Library Resources. 10987654321 For Robin, Geof frey, and David CONTENTS ACKNOWLEDGMENTS xi OVERTURE xiii CHAPTER 1 The Music Star ts 1 CHAPTER 2 Waltzes from Vienna: Hitchcock’s For gotten Operetta 20 CHAPTER 3 The Man Who Knew Too Much: Storm Clouds over Royal Alber t Hall 31 CHAPTER 4 Musical Minimalism: British Hitchcock 39 CHAPTER