H. Hinsberger,1 S. Miesbach,2 and H. J. Pesch3
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Spielplan Oberliga Süd Hauptrunde 2017-18
Hauptrundenspielplan Oberliga-Süd 2017/2018 Spieltag Datum Uhrzeit Heim Gast Spielort 1 29.09.17 20:00 ECDC Memmingen Indians Selber Wölfe Eissporthalle am Hühnerberg 1 29.09.17 20:00 Blue Devils Weiden Deggendorfer SC Hans-Schröpf-Arena 1 29.09.17 20:00 ERC Bulls Sonthofen EV Lindau Islanders Eissporthalle Sonthofen 1 29.09.17 20:00 TEV Miesbach EC Peiting Eisstadion Miesbach 1 29.09.17 19:30 EV Landshut Eisbären Regensburg Eisstadion am Gutenbergweg 1 29.09.17 19:45 EHC Waldkraiburg "Die Löwen" Starbulls Rosenheim Raiffeisen Arena 2 01.10.17 18:00 Selber Wölfe ERC Bulls Sonthofen Netzsch-Arena 2 01.10.17 18:00 EV Lindau Islanders Blue Devils Weiden Eissportarena Lindau 2 01.10.17 18:30 Deggendorfer SC ECDC Memmingen Indians Eisstadion Deggendorf 2 01.10.17 18:00 EC Peiting EHC Waldkraiburg "Die Löwen" Eisstadion Peiting 2 01.10.17 17:00 Starbulls Rosenheim EV Landshut emilo-Stadion 2 01.10.17 18:00 Eisbären Regensburg TEV Miesbach Donau-Arena 3 06.10.17 20:00 Selber Wölfe Blue Devils Weiden Netzsch-Arena 3 06.10.17 20:00 Deggendorfer SC EV Lindau Islanders Eisstadion Deggendorf 3 06.10.17 20:00 ECDC Memmingen Indians ERC Bulls Sonthofen Eissporthalle am Hühnerberg 3 06.10.17 19:30 EC Peiting EV Landshut Eisstadion Peiting 3 06.10.17 20:00 Eisbären Regensburg Starbulls Rosenheim Donau-Arena 3 06.10.17 20:00 TEV Miesbach EHC Waldkraiburg "Die Löwen" Eisstadion Miesbach 4 08.10.17 18:30 Blue Devils Weiden ECDC Memmingen Indians Hans-Schröpf-Arena 4 08.10.17 18:00 EV Lindau Islanders Selber Wölfe Eissportarena Lindau 4 08.10.17 18:00 ERC -

High Voltage Direct Current Transmission – Proven Technology for Power Exchange
www.siemens.com/energy/hvdc High Voltage Direct Current Transmission – Proven Technology for Power Exchange Answers for energy. 2 Contents Chapter Theme Page 1 Why High Voltage Direct Current? 4 2 Main Types of HVDC Schemes 6 3 Converter Theory 8 4 Principle Arrangement of an HVDC Transmission Project 11 5 Main Components 14 5.1 Thyristor Valves 14 5.2 Converter Transformer 18 5.3 Smoothing Reactor 20 5.4 Harmonic Filters 22 5.4.1 AC Harmonic Filter 22 5.4.2 DC Harmonic Filter 25 5.4.3 Active Harmonic Filter 26 5.5 Surge Arrester 28 5.6 DC Transmission Circuit 31 5.6.1 DC Transmission Line 31 5.6.2 DC Cable 32 5.6.3 High Speed DC Switches 34 5.6.4 Earth Electrode 36 5.7 Control & Protection 38 6 System Studies, Digital Models, Design Specifications 45 7 Project Management 46 3 1 Why High Voltage Direct Current? 1.1 Highlights from the High Voltage Direct In 1941, the first contract for a commercial HVDC Current (HVDC) History system was signed in Germany: 60 MW were to be supplied to the city of Berlin via an underground The transmission and distribution of electrical energy cable of 115 km length. The system with ±200 kV started with direct current. In 1882, a 50-km-long and 150 A was ready for energizing in 1945. It was 2-kV DC transmission line was built between Miesbach never put into operation. and Munich in Germany. At that time, conversion between reasonable consumer voltages and higher Since then, several large HVDC systems have been DC transmission voltages could only be realized by realized with mercury arc valves. -

Erziehungsbeistandschaft in Den Landkreisen Rosenheim Und
So erreichen Sie uns Ansprechpartner Kinder, Jugend und Familie Beraten und unterstützen Uli Meyrl, Bereichsleiter Dipl. Sozialpädagoge (FH) Büro Region Rosenheim Wann hilft die Ludwigsplatz 6a · 83022 Rosenheim Erziehungsbeistandschaft? Mobil: 0151 140 88 441 E-Mail: [email protected] Die Erziehungsbeistandschaft unterstützt Eltern, die sich mit der Erziehung ihres Kindes überfordert fühlen Regionalbüro Mangfalltal, Landkreis Rosenheim und hilft Kindern, Jugendlichen und jungen Volljäh- Hasslerstraße 1b · 83059 Kolbermoor rigen, die wegen Entwicklungsproblemen besonderer Unterstützung bedürfen: Regionalbüro Inntal, Landkreis Rosenheim Bahnhofstraße 51 · 83098 Brannenburg Lebensprobleme zu bewältigen, familiäre Konflikten zu lösen, Regionalbüro Miesbach, Landkreis Miesbach Stadtplatz 12 · 83714 Miesbach in den Bereichen Schule und Ausbildung, bei der Freizeitgestaltung, Irschenberg; Kinderdorf Caritas u. Irrtümervorbehalten, 06/2018, Änderungen + Management; Marketing RELATIONS BFL Gestaltung: und Konzeption Irschenberg Kinderkorf – Caritas 6: U. Meyrl Seite 1-5 – iStockphoto; Seiten Fotos: auf dem Weg in die Selbständigkeit und in eine eigene Wohnung, Erziehungsbeistandschaft ein eigenverantwortliches Lebens zu führen. in den Landkreisen Caritas Kinderdorf Irschenberg Miesbacher Straße 22 · D-83737 Irschenberg Rosenheim und Miesbach Telefon: 08062 70950 · Telefax: 08062 709570 „Gemeinsames Handeln eröffnet neue Chancen! www.kinderdorf.de Vertrauen. In unserer Zusammenarbeit mit Jugendlichen www.caritas-von-anfang-an.de -

German Public Authority
Case Study Landkreis Unterallgäu - Landkreis Landshut - Landratsamt Miesbach German Public Authorities Landkreis Unterallgäu, Landkreis Landshut and Landratsamt Miesbach are only three of many German administrative districts that have implemented UDO in Quick View their evolution from a paper-based to an electronic archiving system. The Bavarian district offices chose Plasmon G-Series libraries Powered by Organisation: UDO (Ultra Density Optical) to archive and manage vehicle registration data Landkreis Unterallgäu and improve services offered to the public through easier and faster access to Landkreis Landshut information data. Landratsamt Miesbach All three customers estimate that their UDO archive not only delivers significant cost savings but also improves the efficiency of their initial archive Industry: application for vehicle registration. Public Authority Customer Profile Germany is divided into over 400 administrative Application: districts, which are at an intermediate level of Electronic archive of vehicle administration between the Länder (German states, registration data which collectively make up the Federal Republic of Germany) and the Gemeinden (municipal level). Most districts are Landkreise or rural districts, with some Integrator: cities being districts in their own right (Stadtkreise or BridgeHead urban districts). Solution: The districts have a wide range of responsibilities which are dictated by federal, regional and local laws and Plasmon UDO Technology which include the building and upkeep of roads, hospitals, schools and libraries; social and youth welfare; support for culture; economy and “Not only was UDO the best solution tourism and vehicle registration. All of these responsibilities demand that these important for our archive requirements, it also records be carefully controlled and helped us financially by creating efficiencies maintained. -

Germany (Territory Under Allied Occupation, 1945-1955 : U.S
http://oac.cdlib.org/findaid/ark:/13030/kt0b69r4qg No online items An Inventory of the Germany (Territory under Allied occupation, 1945-1955 : U.S. Zone) Office of Military Government for Bavaria. Kreis Traunstein records Processed by Lyalya Kharitonova. Hoover Institution Archives Stanford University Stanford, California 94305-6010 Phone: (650) 723-3563 Fax: (650) 725-3445 Email: [email protected] © 2010 Hoover Institution Archives. All rights reserved. XX416 1 An Inventory of the Germany (Territory under Allied occupation, 1945-1955 : U.S. Zone) Office of Military Government for Bavaria. Kreis Traunstein records Hoover Institution Archives Stanford University Stanford, California Processed by: Lyalya Kharitonova Date Completed: 2010 Encoded by: Machine-readable finding aid derived from MARC record by David Sun and Supriya Wronkiewicz. © 2010 Hoover Institution Archives. All rights reserved. Collection Summary Title: Germany (Territory under Allied occupation, 1945-1955 : U.S. Zone) Office of Military Government for Bavaria. Kreis Traunstein records Dates: 1945-1948 Collection Number: XX416 Creator: Germany (Territory under Allied occupation, 1945-1955 : U.S. Zone) Office of Military Government for Bavaria. Kreis Traunstein. Collection Size: 13 manuscript boxes (5.2 linear feet) Repository: Hoover Institution Archives Stanford, California 94305-6010 Abstract: The records of American administration of occupied Germany (U.S. Zone), Kreis Traunstein relating to civil administration, including problems of public health and safety, administration of justice, allocation of economic recourses, organization of labor, denazification, and disposition of displaced persons contain memoranda, reports, correspondence, and office files. The collection also presents annual administrative reports on civilian relief efforts for other districts in Bavaria. Physical Location: Hoover Institution Archives Languages: English German Access Collection is open for research. -

Stadtnachrichten 2018
MIESBACHER STADTNACHRICHTEN Nr. 3/ 2018 INFORMATIONEN / MITTEILUNGEN Grußwort Liebe Mitbürgerinnen und Mitbürger, Städtebauförderung war dieser Bürgerbeteili- verehrte Leserinnen und Leser, gungsprozess „Zukunftsgestaltung Marktplatz Miesbach“ sogar förderfähig. In der Stadtratssitzung vom März 2017 be- klagte Stadtrat Markus Seemüller, dass „in Sachen Marktplatz zu viel untersucht wird und zu wenig vorangehe. Er beantragte, eine kleine Arbeitsgruppe zu installieren, die eine tragfähige Kompromisslösung erarbeiten sol- le. Wenn diese es nicht schafft, könne man später immer noch Nonconform beauftragen.“ So erarbeitete dieser AK Marktplatz, beste- hend aus den Stadtratsmitgliedern Astrid Güldner (Grüne), Paul Fertl (SPD), Markus Seemüller (FW) und Dirk Thelemann (CSU), in vielen Stunden einen Vorschlag zur Um- gestaltung, dem der Stadtrat mehrheitlich grünes Licht gab. Gewerbetreibende und Ge- das Thema „Marktplatz“ bewegt die Gemüter, schäftsleute, sowie die Initiative Marktplatz zumindest im Stadtrat. Seit mehr als 20 Jah- und „Leute, die mit dem AK reden wollten“ ren wird insbesondere von Seiten der SPD (Aussage Herr Fertl) wurden eingebunden. diskutiert, diesen verkehrsberuhigt oder ganz Ziel war es, möglichst viele der Parkplätze zu autofrei zu gestalten. erhalten und die Aufenthaltsqualität zu ver- Doch ich möchte beginnen nach dem Motto bessern. „Wie alles begann ab November 2016“: Die Umgestaltung des Marktplatzes ist keine Doch ist das Ziel tatsächlich erreicht worden? leichte Aufgabe, denn die Höhenunterschiede Ist „unsere gute Stube Marktplatz“ durch die zwischen der West- und Ostseite, die fehlen- asymmetrische Anordnung der Parkplätze, de Barrierefreiheit auf der westlichen Seite, der geänderten Straßenführung und der Möb- der schöne Brunnen und der traditionelle Mai- lierung schöner und verkehrssicherer gewor- baum stellen auch Planer vor große Aufga- den? ben. -

36. Infobrief „Familie“ Ostallgäu – Kaufbeuren
Landratsamt Ostallgäu Stadt Kaufbeuren Jugendamt - Familienbildung Abteilung Gleichstellungs- und Isabel Costian Familienbeauftragte Schwabenstraße 11 Elke Schad 87616 Marktoberdorf Berliner Platz 4 | 87600 Kaufbeuren Tel.: 08342 911-510 Tel.: 08341 437-761 [email protected] [email protected] www.familie-ostallgaeu.de www.familie.kaufbeuren.de 07.12.2020 36. Infobrief „Familie“ Ostallgäu – Kaufbeuren Sehr geehrte Damen und Herren, liebe Kolleginnen, liebe Kollegen und Interessierte, die Corona-Pandemie bringt viele Herausforderungen für Familien mit sich und stellt Einrichtungen, die Eltern unterstützend und beratend zur Seite stehen, vor große Aufgaben. Speziell für Fachkräfte hat das Staatsinstitut für Familienforschung in Abstimmung mit dem Bayerischen Familienministerium eine virtuelle Veranstaltungs- und Fortbildungsreihe zur Stärkung der digitalen Kompetenzen auf die Beine gestellt: „kontakt.los! Digitale Bildung und Beratung für Familien“. Die ersten Fortbildungen beginnen unmittelbar im Dezember; der Anmeldeschluss für die ersten Veranstaltungen endet bereits am Dienstag den 8. Dezember 2020. Das Programm mit weiteren Informationen, Teilnahmebedingungen und Anmeldefristen finden Sie unter: https://www.ifb.bayern.de/projekte/neue/45295/index.php. Wir möchten uns herzlich bei Ihnen für die gute Zusammenarbeit und Unterstützung bedanken und wünschen Ihnen eine schöne Adventszeit, frohe Weihnachten und alles Gute für 2021! Mit freundlichen Grüßen Isabel Costian Elke Schad Jugendamt - Familienbildung Abteilung -

ROOTED in the DARK of the EARTH: BAVARIA's PEASANT-FARMERS and the PROFIT of a MANUFACTURED PARADISE by MICHAEL F. HOWELL (U
ROOTED IN THE DARK OF THE EARTH: BAVARIA’S PEASANT-FARMERS AND THE PROFIT OF A MANUFACTURED PARADISE by MICHAEL F. HOWELL (Under the Direction of John H. Morrow, Jr.) ABSTRACT Pre-modern, agrarian communities typified Bavaria until the late-19th century. Technological innovations, the railroad being perhaps the most important, offered new possibilities for a people who had for generations identified themselves in part through their local communities and also by their labor and status as independent peasant-farmers. These exciting changes, however, increasingly undermined traditional identities with self and community through agricultural labor. In other words, by changing how or what they farmed to increasingly meet the needs of urban markets, Bavarian peasant-farmers also changed the way that they viewed the land and ultimately, how they viewed themselves ― and one another. Nineteenth- century Bavarian peasant-farmers and their changing relationship with urban markets therefore serve as a case study for the earth-shattering dangers that possibly follow when modern societies (and individuals) lose their sense of community by sacrificing their relationship with the land. INDEX WORDS: Bavaria, Peasant-farmers, Agriculture, Modernity, Urban/Rural Economies, Rural Community ROOTED IN THE DARK OF THE EARTH: BAVARIA’S PEASANT-FARMERS AND THE PROFIT OF A MANUFACTURED PARADISE by MICHAEL F. HOWELL B.A., Tulane University, 2002 A Thesis Submitted to the Graduate Faculty of The University of Georgia in Partial Fulfillment of the Requirements for the Degree MASTER OF ARTS ATHENS, GEORGIA 2008 © 2008 Michael F. Howell All Rights Reserved ROOTED IN THE DARK OF THE EARTH: BAVARIA’S PEASANT-FARMERS AND THE PROFIT OF A MANUFACTURED PARADISE by MICHAEL F. -
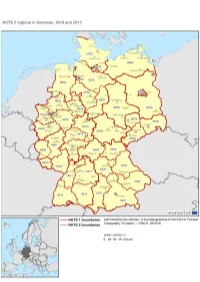
Nuts-Map-DE.Pdf
GERMANY NUTS 2013 Code NUTS 1 NUTS 2 NUTS 3 DE1 BADEN-WÜRTTEMBERG DE11 Stuttgart DE111 Stuttgart, Stadtkreis DE112 Böblingen DE113 Esslingen DE114 Göppingen DE115 Ludwigsburg DE116 Rems-Murr-Kreis DE117 Heilbronn, Stadtkreis DE118 Heilbronn, Landkreis DE119 Hohenlohekreis DE11A Schwäbisch Hall DE11B Main-Tauber-Kreis DE11C Heidenheim DE11D Ostalbkreis DE12 Karlsruhe DE121 Baden-Baden, Stadtkreis DE122 Karlsruhe, Stadtkreis DE123 Karlsruhe, Landkreis DE124 Rastatt DE125 Heidelberg, Stadtkreis DE126 Mannheim, Stadtkreis DE127 Neckar-Odenwald-Kreis DE128 Rhein-Neckar-Kreis DE129 Pforzheim, Stadtkreis DE12A Calw DE12B Enzkreis DE12C Freudenstadt DE13 Freiburg DE131 Freiburg im Breisgau, Stadtkreis DE132 Breisgau-Hochschwarzwald DE133 Emmendingen DE134 Ortenaukreis DE135 Rottweil DE136 Schwarzwald-Baar-Kreis DE137 Tuttlingen DE138 Konstanz DE139 Lörrach DE13A Waldshut DE14 Tübingen DE141 Reutlingen DE142 Tübingen, Landkreis DE143 Zollernalbkreis DE144 Ulm, Stadtkreis DE145 Alb-Donau-Kreis DE146 Biberach DE147 Bodenseekreis DE148 Ravensburg DE149 Sigmaringen DE2 BAYERN DE21 Oberbayern DE211 Ingolstadt, Kreisfreie Stadt DE212 München, Kreisfreie Stadt DE213 Rosenheim, Kreisfreie Stadt DE214 Altötting DE215 Berchtesgadener Land DE216 Bad Tölz-Wolfratshausen DE217 Dachau DE218 Ebersberg DE219 Eichstätt DE21A Erding DE21B Freising DE21C Fürstenfeldbruck DE21D Garmisch-Partenkirchen DE21E Landsberg am Lech DE21F Miesbach DE21G Mühldorf a. Inn DE21H München, Landkreis DE21I Neuburg-Schrobenhausen DE21J Pfaffenhofen a. d. Ilm DE21K Rosenheim, Landkreis DE21L Starnberg DE21M Traunstein DE21N Weilheim-Schongau DE22 Niederbayern DE221 Landshut, Kreisfreie Stadt DE222 Passau, Kreisfreie Stadt DE223 Straubing, Kreisfreie Stadt DE224 Deggendorf DE225 Freyung-Grafenau DE226 Kelheim DE227 Landshut, Landkreis DE228 Passau, Landkreis DE229 Regen DE22A Rottal-Inn DE22B Straubing-Bogen DE22C Dingolfing-Landau DE23 Oberpfalz DE231 Amberg, Kreisfreie Stadt DE232 Regensburg, Kreisfreie Stadt DE233 Weiden i. -

Establishing US Military Government: Law and Order in Southern Bavaria 1945
Portland State University PDXScholar Dissertations and Theses Dissertations and Theses 11-4-1994 Establishing US Military Government: Law and Order in Southern Bavaria 1945 Stephen Frederick Anderson Portland State University Follow this and additional works at: https://pdxscholar.library.pdx.edu/open_access_etds Part of the History Commons Let us know how access to this document benefits ou.y Recommended Citation Anderson, Stephen Frederick, "Establishing US Military Government: Law and Order in Southern Bavaria 1945" (1994). Dissertations and Theses. Paper 4689. https://doi.org/10.15760/etd.6573 This Thesis is brought to you for free and open access. It has been accepted for inclusion in Dissertations and Theses by an authorized administrator of PDXScholar. Please contact us if we can make this document more accessible: [email protected]. THESIS APPROVAL The abstract and thesis of Stephen Frederick Anderson for the Master of Arts in History were presented November 4, 1994. and accepted by the thesis committee and the department. COMMITTEE APPROVALS: Franklin C. West, Chair Charles A. Tracy Representative of the Office of Graduate Stuil DEPARTMENT APPROVAL: David A. Jo Department * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * ACCEPTED FOR PORTLAND STATE UNIVERSITY BY THE LIBRARY on c:z;r 4-M;t?u£;.~ /99'1 ABSTRACT An abstract for the thesis of Stephen Frederick Anderson for the Master of Arts in Histoty presented November 4, 1994. Title: Establishing US Militaty Government: Law and Order in Southern Bavaria 1945. In May 1945, United States Militaty Government (MG) detachments arrived in assigned areas of Bavaria to launch the occupation. By the summer of 1945, the US occupiers became the ironical combination of stern victor and watchful master. -

Military Government Officials, US Policy, and the Occupation of Bavaria, 1945-1949
Coping with Crisis: Military Government Officials, U.S. Policy, and the Occupation of Bavaria, 1945-1949 By Copyright 2017 John D. Hess M.A., University of Kansas, 2013 B.S., Oklahoma State University, 2011 Submitted to the graduate degree program in the Department of History and the Graduate Faculty of the University of Kansas in partial fulfillment of the requirements for the degree of Doctor of Philosophy. Chair: Adrian R. Lewis Theodore A. Wilson Sheyda Jahanbani Erik R. Scott Mariya Omelicheva Date Defended: 28 April 2017 The dissertation committee for John D. Hess certifies that this is the approved version of the following dissertation: Coping with Crisis: Military Government Officials, U.S. Policy, and the Occupation of Bavaria, 1945-1949 Chair: Adrian R. Lewis Date Approved: 28 April 2017 ii Abstract This dissertation explores the implementation of American policy in postwar Germany from the perspective of military government officers and other occupation officials in the Land of Bavaria. It addresses three main questions: How did American military government officials, as part of the institution of the Office of Military Government, Bavaria (OMGB), respond to the challenges of the occupation? How did these individuals interact with American policy towards defeated Germany? And, finally, how did the challenges of postwar Germany shape that relationship with American policy? To answer these questions, this project focuses on the actions of military government officers and officials within OMGB from 1945 through 1949. Operating from this perspective, this dissertation argues that American officials in Bavaria possessed a complicated, often contradictory, relationship with official policy towards postwar Germany. -

OECD Territorial Grids
BETTER POLICIES FOR BETTER LIVES DES POLITIQUES MEILLEURES POUR UNE VIE MEILLEURE OECD Territorial grids August 2021 OECD Centre for Entrepreneurship, SMEs, Regions and Cities Contact: [email protected] 1 TABLE OF CONTENTS Introduction .................................................................................................................................................. 3 Territorial level classification ...................................................................................................................... 3 Map sources ................................................................................................................................................. 3 Map symbols ................................................................................................................................................ 4 Disclaimers .................................................................................................................................................. 4 Australia / Australie ..................................................................................................................................... 6 Austria / Autriche ......................................................................................................................................... 7 Belgium / Belgique ...................................................................................................................................... 9 Canada ......................................................................................................................................................