On the Existence of Partitioned Incomplete Latin Squares with Five Parts
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

12. FORMULATION of the URBAN TRANSPORT MASTER PLAN Development of the RSTP Urban Transportation Master Plan (1) Methodology
The Project on The Revision and Updating of the Strategic Transport Plan for Dhaka (RSTP) Final Report 12. FORMULATION OF THE URBAN TRANSPORT MASTER PLAN Development of the RSTP Urban Transportation Master Plan (1) Methodology The development of the RSTP Urban Transportation Master Plan adopted the following methodology (see Figure 12.1): (i) Elaborate the master plan network through a screen line analysis by comparing the network capacity and future demand. (ii) Identify necessary projects to meet future demand at the same time avoiding excessive capacity. (iii) Conducts economic evaluation of each project to give priority on projects with higher economic return. (iv) Conduct preliminary environmental assessment of every project and consider countermeasures against environmental problems, if any. (v) Make a final prioritization of all physical projects by examining their respective characteristics from different perspectives. (vi) Classify the projects into three categories, namely short-, medium- and long-term projects, by considering the financial constraints. (vii) Prepare an action plan for short-term projects together with “soft” measures. Mid-term Project Source: RSTP Study Team Figure 12.1 Development Procedure for the Master Plan 12-1 The Project on The Revision and Updating of the Strategic Transport Plan for Dhaka (RSTP) Final Report (2) Output of the Transportation Network Plan The RSTP urban transportation network plan was developed based on a review and a modification of the STP network plan. The main points of the modification or adoption of the STP network master plan are as follows: i. Harmonization with future urban structure, land-use plan and development of network plan. -

Effect of Nitrogen and Boron on the Yield of Wheat Cv. Kanchan
J. Bangladesh Agril. Univ. 3(2): 215-220, 2005 ISSN 1810-3030 Effect of nitrogen and boron on the yield of wheat cv. Kanchan M.M. Khan', A.K. Hasan2, M.H. Rashid2, and F. Ahrned3 Palli Karma Sahayak Foundation (PKSF), Sher-e-Banglanagar, Dhaka, 2Department of Agronomy and 3 Department of Agroforestry, Bangladesh Agricultural University, Mymensingh Abstract An experiment was carried out at the Agronomy Field Laboratory, Bangladesh Agricultural University, Mymensingh during the period from January to April 2004 to study the effect of different levels of nitrogen and boron on the yield of wheat cv. Kanchan. The treatments included four levels of nitrogen VIZ., 45, 60, 85 and 110 kg N ha-1 and four levels of boron viz., 0, 1, 2 and 3 kg B ha-1. The experiment was laid out in a Randomized Complete Block Design with three replications. The results revealed that Yield and yield contributing characters were influenced significantly by both levels of nitrogen and boron. Among the levels of nitrogen, 110 kg N ha-1 produced the highest grain (5.54 t ha-1)and straw (8.21 t ha-1 ) yields. The lowest grain (3.23 t ha-1) and straw (5.52 t ha-1) yields were observed with the application of 45 kg N ha-1. The highest grain (4.95 t ha-1)and straw (7.38 t ha 1) yields were produced With 3 kg B ha-1. The minimum grain (3.59 t ha-1)and straw (6.14 t ha-1)yields were found in the control treatment. -

Connecting Bangladesh: Economic Corridor Network
Connecting Bangladesh: Economic Corridor Network Economic corridors are anchored on transport corridors, and international experience suggests that the higher the level of connectivity within and across countries, the higher the level of economic growth. In this paper, a new set of corridors is being proposed for Bangladesh—a nine-corridor comprehensive integrated multimodal economic corridor network resembling the London Tube map. This paper presents the initial results of the research undertaken as an early step of that development effort. It recommends an integrated approach to developing economic corridors in Bangladesh that would provide a strong economic foundation for the construction of world-class infrastructure that, in turn, could support the growth of local enterprises and attract foreign investment. About the Asian Development Bank COnnecTING BANGLADESH: ADB’s vision is an Asia and Pacific region free of poverty. Its mission is to help its developing member countries reduce poverty and improve the quality of life of their people. Despite the region’s many successes, it remains home to a large share of the world’s poor. ADB is committed to reducing poverty through inclusive economic growth, environmentally sustainable growth, and regional integration. ECONOMIC CORRIDOR Based in Manila, ADB is owned by 67 members, including 48 from the region. Its main instruments for helping its developing member countries are policy dialogue, loans, equity investments, guarantees, grants, NETWORK and technical assistance. Mohuiddin Alamgir -

July 2016 Volume 3 No 3
6 VOLUME 3 NO 3 JULY 2016 DHAKA CENTRAL INTERNATIONAL MEDICAL COLLEGE JOURNAL (APPROVED BY BMDC) July 2016, Vol. 3 No. 3 Contents From the Desk of Editor-in-Chief 3 Instructions for Authors 4 Editorial Novel Treatment of Diabetic Nephropathy 12 Original Articles Incidence of Malignancy in Thyroid Nodule 14 Abedin SAMA, Alam MM, Islam MS, Fakir MAY Dyslipidemia and Atherogenic Index among the 21 Young Female Doctors ofBangladesh. Khanduker S, Hoque MM, Khanduker N, Chowdhury MAA, Nazneen M A Study on Stroke in Young Patients due to Cardiac 26 Disease in a Tertiary Care Hospital in Dhaka City Mukta M, Mohammad QD, Mir AS Variation of Transverse Diameter ofDry Ossified 33 Human Atlas Vertebra of Male and Female Rahman S, Ara S, Sayeed S, Rashid S, Ferdous Z, Kashem K Study on Health Effects of Teenage Pregnancies among the Patients 36 Attending Antenatal Care Centre of Chittagong Medical College Hospital Tarafdar MA, Begum N, Das SR, Begum S, Sultana A, Rahman R, Begum R Identification ofDifferent Clinical Features and Complications of 41 Type 2 Diabetes Mellitus in Bengaladeshi Males Begum F, Shamim KM, Akter S, Hossain S, Nazma N, Afrin M, Moureen A Review Articles Female Genital Tuberculosis- A Review Article 46 Shaheed S, Mamun SMAA, Khanom M Case Reports Round Worm induced Acute Appendicitis- an Incidental 51 Finding during Colonoscopy Masum QAA, Islam MN 1 Dhaka Central International Medical College Journal Vol.13 No. 3July 2016 An Official Organ of Dhaka Central International Medical College CHIEF PATRON ADVISORS The Dhaka Central International Prof. Md. Anwarul Islam Md. -
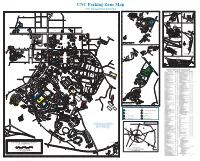
UNC Parking Zone Map UNC Transportation & Parking
UNC Parking Zone Map UNC Transportation & Parking Q R S T U V W X Y Z A B C D E F G H I J K L M N O P 26 **UNC LEASES SPACE CAROLINA . ROAD IN THESE BUILDINGS 21 21 MT HOMESTEAD NORTH LAND MGMT. PINEY OPERATIONS CTR. VD. (NC OFFICE HORACE WILLIAMS AIRPORT VD., HILL , JR. BL “RR” 41 1 1 Resident 41 CommuterRR Lot R12 UNC VD AND CHAPEL (XEROX) TE 40 MLK BL A PRINTING RIVE EXTENSION MLK BL ESTES D SERVICES TIN LUTHER KING TERST PLANT N O I AHEC T EHS HOMESTEAD ROAD MAR HANGER VD. 86) O I-40 STORAGE T R11 TH (SEE OTHER MAPS) 22 22 O 720, 725, & 730 MLK, JR. BL R1 T PHYSICAL NOR NORTH STREET ENVRNMEN HL .3 MILES TO TH. & SAFETY ESTES DRIVE 42 COMMUTER LOT T. 42 ER NC86 ELECTRICAL DISTRICENTBUTION OPERATIONS SURPLUS WA REHOUSE N1 ST GENERAL OREROOM 2 23 23 2 R1 CHAPEL HILL ES MLK JR. BOULE NORTH R1 ARKING ARD ILITI R1 / R2OVERFLOW ZONEP V VICES C R A F SHOPS GY SE EY 43 RN 43 ENERBUILDING CONSTRUCTION PRITCHARD STREET R1 NC 86 CHURCH STREET . HO , JR. BOULE ES F R1 / V STREET SER L BUILDING VICE ARD A ST ATIO GI EET N TR AIRPOR R2 S T DRIVE IN LUTHER KING BRANCH T L MAR HIL TH WEST ROSEMARY STREET EAST ROSEMARY STREET L R ACILITIES DRIVE F A NO 24 STUDRT 24 TH COLUMBI IO CHAPE R ADMINIST OFF R NO BUILDINGICE ATIVE R10 1700 N9 MLK 208 WEST 3 N10 FRANKLIN ST. -

Supporting Material 1,2,4,3-Triazaborole-Based Neutral
Electronic Supplementary Material (ESI) for ChemComm. This journal is © The Royal Society of Chemistry 2014 Supporting Material 1,2,4,3-Triazaborole-based Neutral Oxoborane Stabilized by a Lewis Acid Ying Kai Loh,‡ Che Chang Chong,‡ Rakesh Ganguly, Yongxin Li, Dragoslav Vidovic, and Rei Kinjo* Division of Chemistry and Biological Chemistry School of Physical and Mathematical Sciences Nanyang Technological University 21 Nanyang link Singapore 637371 (Singapore) Contents: Synthesis, physical and spectroscopic data for all new compounds Theoretical results and IR spectrum References NMR spectra 1. Synthesis, physical and spectroscopic data for all new compounds General considerations: All reactions were performed under an atmosphere of argon by using standard Schlenk or dry box techniques; solvents were dried over Na metal, K metal or CaH2. Reagents were of analytical grade, obtained from commercial suppliers and used without further purification. 1H, 13C, 11B, and 27Al{1H} NMR spectra were obtained with a Bruker AV 300, Bruker AV 400 or Bruker AVIII 400MHz BBFO1, spectrometers at 298 K unless otherwise stated. NMR multiplicities are abbreviated as follows: s = singlet, d = doublet, t = triplet, sept = septet, m = multiplet, br = broad signal. Coupling constants J are given in Hz. Electrospray ionization (ESI) mass spectra were obtained at the Mass Spectrometry Laboratory at the Division of Chemistry and Biological Chemistry, Nanyang Technological University. Melting points were measured with OptiMelt Stanford Research System. IR spectrum was measured using Shimadzu IR Prestige-21 FITR spectrometer. N-(2,6-diisopropylphenyl)pivalimidoyl chloride [(DippN=C(tBu)Cl)] was synthesized according to literature report.[1] Synthesis of compound 1: 1 was generated in situ using a modified literature procedure.[2] Phenyl hydrazine (0.99 t mL, 10.0 mmol) and NEt3 (2.09 mL, 15.0 mmol) were added dropwise to a THF solution of [(DippN=C( Bu)Cl)] (2.80 g, 10.0 mmol). -

Connecting South Asia and Southeast Asia: a Bangladesh Country Study
ADBI Working Paper Series Connecting South Asia and Southeast Asia: A Bangladesh Country Study Mustafizur Rahman, Khondaker Golam Moazzem, Mehruna Islam Chowdhury, and Farzana Sehrin No. 500 September 2014 Asian Development Bank Institute Mustafizur Rahman is executive director, Centre for Policy Dialogue (CPD), Bangladesh. Khondaker Golam Moazzem is an additional research director, CPD. Mehruna Islam Chowdhury is a senior research associate, CPD. Farzana Sehrin is a research associate, CPD. The authors would like to thank the paper reviewers and participants at the meeting organized by ADB in Manila, 6–7 November 2013. They also would like to express their sincere appreciation for the support provided by the ADBI staff who helped in preparing this manuscript for publication. The views expressed in this paper are the views of the authors and do not necessarily reflect the views or policies of ADBI, ADB, its Board of Directors, or the governments they represent. ADBI does not guarantee the accuracy of the data included in this paper and accepts no responsibility for any consequences of their use. Terminology used may not necessarily be consistent with ADB official terms. Working papers are subject to formal revision and correction before they are finalized and considered published. The Working Paper series is a continuation of the formerly named Discussion Paper series; the numbering of the papers continued without interruption or change. ADBI’s working papers reflect initial ideas on a topic and are posted online for discussion. ADBI encourages readers to post their comments on the main page for each working paper (given in the citation below). -
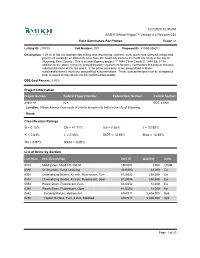
Classification Ratings Project Information B = 0.12% Cb = 41.71
12/7/2020 12:35 PM AASHTOWare Project™ Version 4.4 Revision 034 Cost Summaries For Primes Report v1 Letting ID: 210108 Call Number: 001 Proposal ID: 41000-206011 Description: 1.29 mi of hot mix asphalt cold milling and resurfacing, concrete curb, gutter and sidewalk ramps and pavement markings on Wilson Avenue from the south city limits to the north city limits in the city of Wyoming, Kent County. This is a Local Agency project. ** 1444 Cb or Comb/Jt. 1444 Ea, J **In addition to the above minimum prequalification requirement for prime contractors this project includes subclassifications of Cb, Ea and J. If the prime contractor is not prequalified in those subclassifications it must use prequalified subcontractors. Those subcontractors must be designated prior to award of the contract to the confirmed low bidder. DBE Goal Percent: 0.00% Project Information Project Number Federal Project Number Federal Item Number Control Section 206011A N/A EDC 41000 Location: Wilson Avenue from south city limits to north city limits in the city of Wyoming. Route: Classification Ratings B = 0.12% Cb = 41.71% Ea = 7.86% J = 12.92% K = 2.83% L = 0.48% MOT = 13.65% Misc = 13.46% N3 = 0.97% N93A = 6.00% List of Items by Section Line Num Item Description Item ID Quantity Units 0010 Mobilization, Max$131,300.00 1500001 1.000 LSUM 0090 Dr Structure, Temp Lowering 4030390 44.000 Ea 0300 Channelizing Device, 42 inch, Fluorescent, Furn 8120035 250.000 Ea 0310 Channelizing Device, 42 inch, Fluorescent, Oper 8120036 250.000 Ea 0350 Plastic Drum, Fluorescent, Furn -
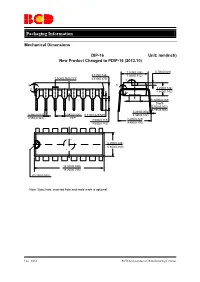
Mechanical-Dimensions-BCD.Pdf
Packaging Information Mechanical Dimensions DIP-16 Unit: mm(inch) New Product Changed to PDIP-16 (2013.10) 7.320(0.288) 0.700(0.028) 3.710(0.146) 7.920(0.312) 1.524(0.060) TYP 4.310(0.170) 5° 6° 6° 4° 3.200(0.126) 4° 3.600(0.142) Φ3.000(0.118) Depth 0.050(0.002) 0.150(0.006) 0.204(0.008) 0.360(0.014) 2.540(0.100) 0.510(0.020)MIN 0.360(0.014) 0.560(0.022) TYP 3.000(0.118) 8.200(0.323) 3.600(0.142) 9.400(0.370) 6.200(0.244) 6.600(0.260) 18.800(0.740) 19.200(0.756) R0.750(0.030) Note: Eject hole, oriented hole and mold mark is optional. Dec. 2014 BCD Semiconductor Manufacturing Limited Packaging Information Mechanical Dimensions DIP-16 (Special for AZ4052) Unit: mm(inch) 7.320(0.288) 0.700(0.028) 3.710(0.146) 7.920(0.312) 1.524(0.060)T YP 4.310(0.170) 5 ° 6 ° 6 ° 4 ° 3.200(0.126) 4 ° 3.600(0.142) Φ3.000(0.118) Depth 0.050(0.002) 0.150(0.006) 0.204(0.008) 0.360(0.014) 2.540(0.100) 0.510(0.020)MIN 0.360(0.014 ) 0.560(0.022) TYP 3.000(0.118) 8.500(0.335) 3.600(0.142) TYP 6.200(0.244) 6.600(0.260) 18.800(0.740) 19.200(0.756) R0.750(0.030) Note: Eject hole, oriented hole and mold mark is optiona.l Dec. -

The Completeness and Vulnerability of Road Network in Bangladesh
M. A. Ali, S. M. Seraj and S. Ahmad (eds): ISBN 984-823-002-5 The Completeness and Vulnerability of Road Network in Bangladesh A. S. M. Abdul Quium and S. A. M. Aminul Hoque Department of Urban and Regional Planning Bangladesh University of Engineering and Technology, Dhaka-1000, Bangladesh Abstract Road transportation has emerged as the most popular mode of transportation in Bangladesh. Despite being the most popular mode, it suffers heavily from network failures due to natural as well as man-made disruptions. This paper presents the major findings of a study relating to the completeness of the road network with respect to the pattern of traffic flow and its vulnerability with reference to the disruptions caused by the flood of 1998. The study considered development of road network by regions on the basis of degree of network completeness by connectivity indices namely, γ and α indices that apply the Graph Theory to measure the geometric pattern of a network. The analysis revealed that the road network development in Bangladesh at the national and regional levels is still in its early stage. The existing network has a very few circuits for movement at all the levels and, therefore, susceptible to high risk of disruption. In terms of circuitry, the network has a bare marginal grid configuration at the divisional and national levels. The present overwhelming dependence on road transportation system will continue in the future. In this context, completeness of the whole road network should be considered in all future road planning exercises. Assessment of vulnerability of links around Dhaka deserves special consideration as any link failure of the national highways around Dhaka affects almost the whole system. -

Land Resource Appraisal of Bangladesh for Agricultural
BGD/81/035 Technical Report 3 Volume II LAND RESOURCES APPRAISAL OF BANGLADESH FOR AGRICULTURAL DEVELOPMENT REPORT 3 LAND RESOURCES DATA BASE VOLUME II SOIL, LANDFORM AND HYDROLOGICAL DATA BASE A /UNITED NATIONS DEVELOPMENT PROGRAMME FAo FOOD AND AGRICULTURE ORGANIZATION vJ OF THE UNITED NATIONS BGD/81/035 Technical Report 3 Volume II LAND RESOURCES APPRAISAL OF BANGLADESH FOR AGRICULTURALDEVELOPMENT REPORT 3 LAND RESOURCES DATA BASE VOLUME II SOIL, LANDFORM AND HYDROLOGICAL DATA BASE Report prepared for the Government of the People's Republic of Bangladesh by the Food and Agriculture Organization of the United Nations acting as executing agency for the United Nations Development Programme based on the work of H. Brammer Agricultural Development Adviser J. Antoine Data Base Management Expert and A.H. Kassam and H.T. van Velthuizen Land Resources and Agricultural Consultants UNITED NATIONS DEVELOPMENT PROGRAMME FOOD AND AGRICULTURE ORGANIZATION OF THE UNITED NATIONS Rome, 1988 The designations employed and the presentation of material in this publication do not imply the expression of any opinion whatsoever on the part of the Food and AgricultureOrganization of the United Nations concerning the legal status of any country, territory, city or area or of its authorities, or concerning the delimitation of its frontiers or boundaries. All rights reserved. No part of this publication may be reproduced, stored ina retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopyingor otherwise, without the prior perrnission of (he copyright owner. Applications for such permission,with a statement of the purpose and extent of the reproduction, should be addressedto the Director, Publications Division, Food and Agriculture Organization of the United Nations, Viadelle Terme di Caracarla, 00100 Home, Italy. -

Bangladesh Agron
Bangladesh Agron. J. 2015, 18(1): 89-98 GROWTH, YIELD AND QUALITY OF WHEAT VARITIES AS AFFECTED BY DIFFERENT LEVELS OF NITROGEN H. Mondal1, S. Mazumder2, S. K. Roy3, T. A. Mujahidi4 and S. K. Paul5 1Department of Agronomy, Sher-e-Bangla Agricultural University, Dhaka-1207, Bangladesh 2Sher-e-Bangla Nagar Adorsha Mohila College, Dhaka-1207, Bangladesh, 3Department of Genetics and Plant Breeding, Sher-e-Bangla Agricultural University, Dhaka-1207, Bangladesh 4Plant Breeding Division, Bangladesh Agricultural Research Institute, Joydebpur, Gazipur-1701, Bangladesh 5Agronomy Division, Bangladesh Agricultural Research Institute, Joydebpur, Gazipur-1701, Bangladesh. E-mail: [email protected] Key Words: Wheat variety, Nitrogen, Protein, Grain quality Abstract A field experiment was conducted at the experimental field of Sher-e-Bangla Agricultural University, Dhaka, Bangladesh during November 2012 to March 2013 to evaluate the response of three (3) wheat varieties viz., BARI Gom23, BARI Gom24 and BARI Gom25 under four levels of nitrogen fertilizer i.e, 75, 100, 125 and 150 kg N ha-1. The experiment was laid out in Randomized Complete Block Design (RCBD) with three replications. Results showed that plant height, number of leaves plant-1, leaf length and dry matter content were significantly affected due to varieties and/or nitrogen levels. Grains ear-1, number of fertile grains plant-1, 1000-grain weight, grain yield and harvest index were also significantly influenced by varieties and/or nitrogen levels. The value of all parameters studied in this experiment increased with increasing nitrogen levels up to 125 kg N ha-1 and thereafter decreased with fertilizer increasing level. Combination results showed that BARI Gom-24 with application of 125 kg N ha-1 gave the maximum grain yield (4.71 t ha-1), harvest index (49.37 %) and protein content (10.88%).