Wavelength Beam Combining for Power and Brightness Scaling of Laser Systems
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

High-Power Solid-State Lasers from a Laser Glass Perspective
LLNL-JRNL-464385 High-Power Solid-State Lasers from a Laser Glass Perspective J. H. Campbell, J. S. Hayden, A. J. Marker December 22, 2010 Internationakl Journal of Applied Glass Science Disclaimer This document was prepared as an account of work sponsored by an agency of the United States government. Neither the United States government nor Lawrence Livermore National Security, LLC, nor any of their employees makes any warranty, expressed or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States government or Lawrence Livermore National Security, LLC. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States government or Lawrence Livermore National Security, LLC, and shall not be used for advertising or product endorsement purposes. High-Power Solid-State Lasers from a Laser Glass Perspective John H. Campbell, Lawrence Livermore National Laboratory, Livermore, CA Joseph S. Hayden and Alex Marker, Schott North America, Inc., Duryea, PA Abstract Advances in laser glass compositions and manufacturing have enabled a new class of high-energy/high- power (HEHP), petawatt (PW) and high-average-power (HAP) laser systems that are being used for fusion energy ignition demonstration, fundamental physics research and materials processing, respectively. The requirements for these three laser systems are different necessitating different glasses or groups of glasses. -
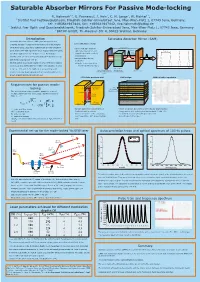
Saturable Absorber Mirrors for Passive Mode-Locking
Saturable Absorber Mirrors For Passive Mode-locking R. Hohmuth1 3, G. Paunescu2, J. Hein2, C. H. Lange3, W. Richter1 3, 1 Institut fuer Festkoerperphysik, Friedrich-Schiller-Universitaet Jena, Max-Wien-Platz 1, 07743 Jena, Germany, tel: +493641947444, fax: +493641947442, [email protected] 2 Institut fuer Optik und Quantenelektronik, Friedrich-Schiller-Universitaet Jena, Max-Wien-Platz 1, 07743 Jena, Germany 3 BATOP GmbH, Th.-Koerner-Str. 4, 99425 Weimar, Germany Introduction Saturable Absorber Mirror (SAM) Saturable absorber mirrors (SAMs) are inexpensive and schematic laser set-up compact devices for passive mode-locking of diode pumped solid state lasers. Such laser systems can provide ultrashort cavity, length L -cavity with gain medium pulse trains with high repetition rates. Typical values for pulse pulse -high reflective mirror and TRT=2L/c ) t output mirror with partially ( duration ranging from 100 fs up to 10 ps. For instance a I y t transmission i s Nd:YAG laser can be mode-locked with pulse duration of 8 ps n e -saturable absorber as t n and mean output power of 6 W. I modulator On this poster we present results for a Yb: KYW laser passive =>pulse trains spaced by mode-locked by SAMs with three different modulation depths round-trip time TRT=2L/c time t between 0.6% and 2.0%. SAMs were prepared by solid- gain medium high reflective mirror (pumped e.g. output mirror source molecular beam epitaxy with a low-temperature (LT) with saturable absorber by laser diode) (SAM) grown InGaAs absorbing quantum well. LT InGaAs quantum well SAM design SAM reflection spectrum Ta O or SiO / dielectric cover Requirements for passive mode- 25 2 conduction 71.2 nm GaAs / barrier E 7 nm c1 71.2 nm GaAs / barrier locking band Ec LT InGaAs 74.7 nm GaAs The mode-locking regime is stable agaist the onset of quantum well InGaAs 88.4 nm AlAs multiple pulsing as long as the pulse duration is smaller energy : 25x Bragg mirror than t . -
![Arxiv:1911.10820V2 [Physics.Optics] 18 Dec 2019](https://docslib.b-cdn.net/cover/7640/arxiv-1911-10820v2-physics-optics-18-dec-2019-2347640.webp)
Arxiv:1911.10820V2 [Physics.Optics] 18 Dec 2019
Hybrid integrated semiconductor lasers with silicon nitride feedback circuits Klaus-J. Boller1,3,*, Albert van Rees1, Youwen Fan1,2, Jesse Mak1, Rob E.M. Lammerink1, Cornelis A.A. Franken1, Peter J.M. van der Slot1, David A.I. Marpaung1, Carsten Fallnich3,1, J¨ornP. Epping2, Ruud M. Oldenbeuving2, Dimitri Geskus2, Ronald Dekker2, Ilka Visscher2, Robert Grootjans2, Chris G.H. Roeloffzen2, Marcel Hoekman2, Edwin J. Klein2, Arne Leinse2, and Ren´eG. Heideman2 1Laser Physics and Nonlinear Optics, Mesa+ Institute for Nanotechnology, Department for Science and Technology, Applied Nanophotonics, University of Twente, Enschede, The Netherlands 2LioniX International BV, Enschede, The Netherlands 3University of M¨unster,Institute of Applied Physics, Germany *Corresponding author: [email protected] December 19, 2019 Abstract Hybrid integrated semiconductor laser sources offering extremely narrow spectral linewidth as well as compati- bility for embedding into integrated photonic circuits are of high importance for a wide range of applications. We present an overview on our recently developed hybrid-integrated diode lasers with feedback from low-loss silicon nitride (Si3N4 in SiO2) circuits, to provide sub-100-Hz-level intrinsic linewidths, up to 120 nm spectral coverage around 1.55 µm wavelength, and an output power above 100 mW. We show dual-wavelength operation, dual-gain operation, laser frequency comb generation, and present work towards realizing a visible-light hybrid integrated diode laser. 1 Introduction The extreme coherence of light generated with lasers has been the key to great progress in science, for instance in testing natures fundamental symmetries [1, 2], properties of matter [3, 4], or for the detection of gravitational waves [5]. -

Laser Output Couplers
Nd:YAG LASER OPTICS LASER OUTPUT COUPLERS An output coupler is a partially reflecting dielectric mirror used in a SUBSTRATE laser cavity. It transmits a part of the circulating intracavity power for Material UV grade Fused Silica or BK7 glass generating a useful output from the laser. S1 Surface Flatness λ/10 typical at 633 nm A low transmission output coupler leads to a low laser threshold, but S1 Surface Quality 20 –10 scratch & dig (MIL-PRF-13830B) also possibly to poor laser efficiency if the losses due to output coupling S2 Surface Flatness λ/10 typical at 633 nm do not dominate over other parasitic losses in the laser cavity. The S2 Surface Quality 20 –10 scratch & dig (MIL-PRF-13830B) output coupler transmission is often chosen to maximize the achieved Diameter Tolerance +0.00 mm; -0.12 mm output power, although its optimum value may be lower or higher if Thickness Tolerance ±0.25 mm there are other design purposes (minimizing the intracavity intensities Parallelism 30 arcsec or suppressing Q-switching instabilities in a passively mode-locked Chamfer 0.3 mm at 45° typical laser). COATING Technology Electron beam multilayer dielectric Adhesion and Durability Per MIL-C-675A. Insoluble in lab solvents Clear Aperture Exceeds central 85% of diameter OPTICS LASER :YAG Damage Threshold: Nd BK7 >3 J/cm2, 8 nsec pulse, 1064 nm typical UV FS >6 J/cm2, 8 nsec pulse, 1064 nm typical Coated Surface Flatness λ/10 at 633 nm over clear aperture Angle of Incidence 0 – 8° (normal) Back side antireflection coated R < 0.2% LASER OUTPUT COUPLERS SIZE -

A Mode Locked Uv-Fel
578 P. Parvin et al. / Proceedings of the 2004 FEL Conference, 578-581 A MODE LOCKED UV-FEL P. Parvin* (AUT, IR-Tehran; AEOI-RCLA, IR-Tehran), G. R. Davoud-Abadi (AUT, IR-Tehran), A. Basam (IHU, IR-Tehran), B. Jaleh (BASU, IR-Hamadan), Z. Zamanipour (AEOI-RCLA, IR- Tehran), B. Sajad (AU, IR-Tehran), F. Ebadpour (AUT, IR-Tehran) Abstract FEL mode-locking phenomena for shorter wavelengths in An appropriate resonator has been designed to generate far-infrared and infrared range of spectrum [13, 14]. femtosecond mode locked pulses in a UV FEL with the In free-electron laser operating at the FIR and IR modulator performance based on the gain switching. The spectral regions, using a radio-frequency accelerator for gain broadening due to electron energy spread affects on the electron beam, when the electron pulse length can be the gain parameters, small signal gain γ0 and saturation of the same order as the slippage length or even shorter, intensity Is, to determine the optimum output coupling as the laser emits short pulses of multimode broad-band well. radiation [14]. INTRODUCTION On the other hand, Storage ring FEL represents a very Today, there is an increasing interest in the generation competitive technical approach to produce photons with of intense, tunable, coherent light in short wavelength these characteristics. After the first lasing of a storage region. Laser pulses of very short duration in UV/VUV ring FEL (SRFEL) in visible [15], the operation spectrum, find applications in large number of areas, such wavelength has been pushed to shorter values in various as analysis of transit-response of atoms and molecules, laboratories. -

Laser Safety
Laser Safety Ronald Breedijk LCAM safety talk Laser Components • Light Amplification by Stimulated Emission of Radiation OPTICAL RESONATOR LASER beam Active medium high reflectance output coupler mirror mirror excitation Associated hazards: 1. Laser Beam: eye injury, burns, skin cancer (UV), fire hazard 2. Excitation source: high voltage, water cooling Ordinary Light vs. Laser Light 1. Many wavelengths 1. Monochromatic 2. Multidirectional 2. Directional 3. Incoherent 3. Coherent These three properties of laser light are what can make it more hazardous than ordinary light. Laser light can deposit a lot of energy within a small area. LASER SPECTRUM Gamma Rays X-Rays Ultra- Visible Infrared Micro- Radar TV Radio violet waves waves waves waves 10-13 10-12 10-11 10-10 10-9 10-8 10-7 10-6 10-5 10-4 10-3 10-2 10-1 1 10 102 Wavelength (m) LASERS Retinal Hazard Region Ultraviolet Visible Near Infrared Far Infrared 200 300 400 500 600 700 800 900 1000 1100 1200 1300 1400 1500 10600 Wavelength (nm) Laser-Professionals.com Setup LSM 510 Argon UV laser – 351nm and 365nm Diode laser – 440nm Argon laser – 488nm and 514nm Hene laser – 543nm DPSS laser – 561nm Hene laser – 633nm Ti:Sapphire laser – 700nm – 1000nm (two photon) SetupA1 excitation Nikon options A1 4 laser box Transmission 640 nm 561 nm 457 nm 405 nm Diode Dpss 488 nm Mercury diode 514 nm AOTF Objectives 1. Plan Apo VC 60x, NA1.40 (oil) 2. Plan Fluor 40x, NA1.3 (oil) 3. Plan Fluor 20x, NA0.75 (M im.) Main dichroic 1. -

The Lasing Characteristics of a Passively Q-Switched Nd:YVO4 Laser Using a Cr:YAG Saturable Absorber
Journal of the Korean Physical Society, Vol. 51, No. 1, July 2007, pp. 322∼326 The Lasing Characteristics of a Passively Q-Switched Nd:YVO4 Laser Using a Cr:YAG Saturable Absorber Jonghoon Yi∗ and Jin Hyuk Kwon Department of Physics, Yeungnam University, Kyungsan 712-749 (Received 31 January 2007) A diode-pumped, passively Q-switched Nd:YVO4 laser was fabricated. A composite crystal, 0.6 % Nd doped YVO4 crystal block bonded with an undoped YVO4 crystal cap, was used. The end cap reduced thermal lensing as well as thermal stress, when the crystal was end pumped by using a fiber coupled diode laser. Cr:YAG crystals with initial transmission of 80 % or 90 % were used as saturable absorbers. For each Cr:YAG crystal, several output couplers with different reflectivity were tested. The variations in the pulsewidth, the pulse repetition rate, and the average output power of the passively Q-switched laser were measured while varying the diode pump power for each value of the output coupler reflectivity and the Cr:YAG initial transmission. The dependences of the lasing characteristics on the output coupler reflectivity and the Cr:YAG initial transmission were explained. PACS numbers: 42.55.Xi, 42.60.Gd, 42.60.Jf Keywords: Cr:YAG laser, Nd:YVO4 laser, Passive Q-switching, Diode-pumped laser, Solid state laser I. INTRODUCTION medium is simple in structure, and small scale lasers can be easily fabricated. Although the thermal problem remains, bulk crystals with both ends diffusion bonded The trend of current laser development targets ro- with undoped crystal can reduce the thermal problem bust, maintenance-free, small, and efficient laser sources. -

LASER (Basic) Light Amplification by Stimulated Emission of Radiation 雷射 (激光)
LASER (basic) Light Amplification by Stimulated Emission of Radiation 雷射 (激光) 倪其焜 中央研究院原子與分子科學研究所 Part I: How does a laser work? -Ei / kT Boltzmann distribution: Pi = Di xe Pi > Pj when Ei < Ej Interaction between light and atoms (molecules) absorption emission Stimulated emission -Ei / kT Boltzmann distribution: Pi = Di x e Pi > Pj when Ei < Ej In average: absorption Population inversion Pi > Pj if Ei > Ej Stimulated emission Design (Population inversion) Gain medium High reflector Output coupler Rear mirror Cavity Intra cavity laser beam > output laser beam At least three energy levels are required 1 laser Pump 2 3 Design Optical switch Gain medium High reflector Output coupler Rear mirror Laser modes of operation • Continuous wave operation (CW) I time • Pulsed operation I time At least three energy levels are required 1 laser Pump 2 3 Design Gain medium High reflector Output coupler Rear mirror Gain medium Output coupler High reflector Rear mirror Part II: More details of lasers Cavity: stable cavity unstable cavity Standing waves Laser modes Cylindrical transverse mode Rectangular transverse patterns TEM(pl) mode patterns TEM(mn) Different modes: different frequencies Single mode laser A single mode laser is called a single frequency laser. The linewidth can be very small and the coherent length is long. Multimode laser A multimode operation causes the linewidth to be wide:a multiple of the mode spacing of the resonator. Polarization Definition: direction of the electric field oscillation Linear polarization horizontal polarization vertical polarization Circular polarization right left Electric field of a laser pulse Beam Divergence • Definition: a measure for how fast a laser beam expands far from its focus • lower-divergence beam is preferable • divergence of a laser beam is proportional to its wavelength and inversely proportional to the diameter of the beam at its narrowest point. -

Development of Laser Technology in Poland – 2016
Development of Laser Technology in Poland – 2016 Zdzisław Jankiewicz1, Jan K. Jabczyński1, Ryszard S. Romaniuk2 1Institute of Optoelectronics, Military University of Technology, Warsaw, Poland 2Institute of Electronic Systems, Warsaw University of Technology, Poland ABSTRACT The paper is an introduction to the volume of proceedings and a concise digest of works presented during the XIth National Symposium on Laser Technology (SLT2016) [1]. The Symposium is organized since 1984 every three years [2-8]. SLT2016 was organized by the Institute of Optoelectronics, Military University of Technology (IO, WAT) [9], Warsaw, with cooperation of Warsaw University of Technology (WUT) [10], in Jastarnia on 27-30 September 2016. Symposium Proceedings are traditionally published by SPIE [11-19]. The meeting has gathered around 150 participants who presented around 120 research and technical papers. The Symposium, organized every 3 years is a good portrait of laser technology and laser applications development in Poland at university laboratories, governmental institutes, company R&D laboratories, etc. The SLT also presents the current technical projects under realization by the national research, development and industrial teams. Topical tracks of the Symposium, traditionally divided to two large areas – sources and applications, were: laser sources in near and medium infrared, picosecond and femtosecond lasers, optical fiber lasers and amplifiers, semiconductor lasers, high power and high energy lasers and their applications, new materials and components for laser technology, applications of laser technology in measurements, metrology and science, military applications of laser technology, laser applications in environment protection and remote detection of trace substances, laser applications in medicine and biomedical engineering, laser applications in industry, technologies and material engineering. -

The Dye Laser •••: »
CHAPTER 2. THE DYE LASER •••: » •1 THE DYE OSCILLATOR AND WAVELENGTH MONITORING UNIT [THE DYE OSCILLATOR (CLOSE UP) 2.1 INTRODUCTION It is a wellknown fact, that the lasers have played a key- role in the foundation and development of modern spectroscopic techniques. The organic dye lasers in particular, have captured a great deal of attention due to their continuous wavelength tunability, indeed, many visible wavelength lasers are known but have been eclipsed by this important advantage of organic dye lasers. In other words, this laser is the spectroscopist's dream, in that its wavelength can be precisely controlled in every applicable parameter space. Both, the output wavelength and the bandwidth can be accurately determined. In addition, the time duration of the output is variable from continuous wave to subpicosecond pulse regime. Moreover these lasers operate with competitive working efficiencies with other lasers and cover not only the entire visible region but also the ultra-violet and infra-red region of the electro-magnetic spectrum. No wonder, dye lasers have found various diversified field applications. The complete design and fabricational details of a narrow linewidth, multiple prism pulsed dye oscillator is presented in this chapter. The technological development in the design modification of the dye resonators, their comparative study, the design and fabrication considerations and the working of the dye oscillator along with the laser parametric measurements are thoroughly discussed. A brief description of the nitrogen laser, used to pump the dye laser, is also incorporated in this chapter. 2.2 SPECTROSCOPY OF TEE DYE MOLECULE The laser action in the solution containing organic dye was realized, first, by P.P. -

Terahertz Time Domain Spectroscopy and Fresnel Coefficient Based Predictive Model
Wright State University CORE Scholar Browse all Theses and Dissertations Theses and Dissertations 2012 Terahertz Time Domain Spectroscopy and Fresnel Coefficient Based Predictive Model Justin C. Wheatcroft Wright State University Follow this and additional works at: https://corescholar.libraries.wright.edu/etd_all Part of the Physics Commons Repository Citation Wheatcroft, Justin C., "Terahertz Time Domain Spectroscopy and Fresnel Coefficient Based edictivPr e Model" (2012). Browse all Theses and Dissertations. 623. https://corescholar.libraries.wright.edu/etd_all/623 This Thesis is brought to you for free and open access by the Theses and Dissertations at CORE Scholar. It has been accepted for inclusion in Browse all Theses and Dissertations by an authorized administrator of CORE Scholar. For more information, please contact [email protected]. TERAHERTZ TIME-DOMAIN SPECTROSCOPY AND FRESNEL COEFFICIENT BASED PREDICTIVE MODEL A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science By JUSTIN C. WHEATCROFT B.S., Kent State University, 2009 2012 Wright State University WRIGHT STATE UNIVERSITY GRADUATE SCHOOL August 31, 2012 I HEREBY RECOMMEND THAT THE THESIS PREPARED UNDER MY SUPERVISION BY Justin C. Wheatcroft ENTITLED Terahertz time domain spectroscopy and Fresnel coefficient based predictive model BE ACCEPTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF Master of Science. ________________________________ Jason A. Deibel, Ph.D. Thesis Director ________________________________ Committee on Final Examination Douglas T. Petkie, Ph.D. Chair, Department of Physics ________________________________ Jason A. Deibel, Ph.D. ________________________________ Douglas T. Petkie, Ph.D. ________________________________ Gregory Kozlowski, Ph.D. ________________________________ Andrew Hsu, Ph.D. Dean, Graduate School ABSTRACT Wheatcroft, Justin C. -

Radiant Dyes Laser & Acc. Gmbh
Radiant Dyes Laser & Acc. GmbH Broadband- & Midband - pulsed dye laser Broadband pulsed dye laser RDP-1 Broadband- dye laser with non-selective cavity. The laser can be equipped with the following pump mirror sets: 2: Beam splitter • Mirror set 1: 330 - 420 nm 3: Lens • Mirror set 2: 420 - 720 nm 4: Output coupler 5: End mirror • Mirror set 3: 550 - 900 nm 6: Dye Cell Dye circulator system RD 250 FC 20 with 20 mm flow cell unit, suitable up to 100 Hz 100 mJ pump energy. This system is also available with RD 1000 FC 40 with 40mm flow cell unit and water cooling for pump energy up to 400 mJ. Conversion efficiency is very high, hardly any losses: Excimer laser pumped [308 nm]: 20% - 473 nm Nd:YAG-laser pumped [532 nm]: 30% - 570 nm Bandwidth (typically): 3 - 5 nm (at the maximum of the laser dye) Midband Pulsed Dye Laser RDP-1M Tunable dye laser, resonator with prism as disperse element and one dye circulator RD 250 FC 20, 10x beam expander Linewidth (typically): approx. 1-2 nm Maximum pump energy: 80 mJ 1: Mirror Tuning range: 330-850 nm 2: Beam splitter 3: Lens 4: End mirror 5: Prism RDP-2M 6: Beam expander 7: Output coupler This system is very close to RDP-1M, 8: Polarisator but with oscillator and 9: Turning Prism amplifier in one 20 mm dye cell. 11: Dye Cell Max. pump energy: 160 mJ. RDP-3M This system is close to RDP-2M, but with oscillator, amplifier in one 20 mm dye cell and main amplifier in a 40 mm dye cell.