DOCSLIB.ORG

Geometric Algebra Primer

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Geometric Algebra Primer Geometric Algebra Primer Jaap Suter March 12, 2003 Abstract Adopted with great enthusiasm in physics, geometric algebra slowly emerges in computational science. Its elegance and ease of use is unparalleled. By introducing two simple concepts, the multivector and its geometric product, we obtain an algebra that allows subspace arithmetic. It turns out that being able to ‘calculate’ with subspaces is extremely powerful, and solves many of the hacks required by traditional methods. This paper provides an introduction to geometric algebra. The intention is to give the reader an understanding of the basic concepts, so advanced material becomes more accessible. Copyright °c 2003 Jaap Suter. Permission to make digital or hard copies of part of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation. Abstracting with credit is per- mitted. To copy otherwise, to republish, to post on servers, or to redistribute to lists, requires prior specific permission and/or a fee. Request permission through email at cliff[email protected]. See http://www.jaapsuter.com for more infor- mation. Contents 1 Introduction 4 1.1 Rationale ............................... 4 1.2 Overview ............................... 4 1.3 Acknowledgements .......................... 5 1.4 Disclaimer ............................... 5 2 Subspaces 6 2.1 Bivectors ............................... 7 2.1.1 The Euclidian Plane ..................... 8 2.1.2 Three Dimensions ...................... 10 2.2 Trivectors ............................... 12 2.3 Blades ................................. 14 3 Geometric Algebra 16 3.1 The Geometric Product ....................... 17 3.2 Multivectors .............................. 17 3.3 The Geometric Product Continued ................. 18 3.4 The Dot and Outer Product revisited ............... 22 3.5 The Inner Product .......................... 23 3.6 Inner, Outer and Geometric ..................... 25 4 Tools 27 4.1 Grades ................................. 27 4.2 The Inverse .............................. 28 4.3 Pseudoscalars ............................. 29 4.4 The Dual ............................... 30 4.5 Projection and Rejection ....................... 31 4.6 Reflections ............................... 34 4.7 The Meet ............................... 36 5 Applications 37 5.1 The Euclidian Plane ......................... 37 5.1.1 Complex Numbers ...................... 37 5.1.2 Rotations ........................... 38 1 5.1.3 Lines .............................. 41 5.2 Euclidian Space ............................ 43 5.2.1 Rotations ........................... 43 5.2.2 Lines .............................. 53 5.2.3 Planes ............................. 53 5.3 Homogeneous Space ......................... 55 5.3.1 Three dimensional homogeneous space ........... 55 5.3.2 Four dimensional homogeneous space ............ 58 5.3.3 Concluding Homogeneous Space .............. 60 6 Conclusion 61 6.1 The future of geometric algebra ................... 62 6.2 Further Reading ........................... 62 2 List of Figures 2.1 The dot product ........................... 6 2.2 Vector a extended along vector b .................. 7 2.3 Vector b extended along vector a .................. 7 2.4 A two dimensional basis ....................... 9 2.5 A 3-dimensional bivector basis ................... 10 2.6 A Trivector .............................. 12 2.7 Basis blades in 2 dimensions ..................... 14 2.8 Basis blades in 3 dimensions ..................... 14 2.9 Basis blades in 4 dimensions ..................... 14 3.1 Multiplication Table for basis blades in C`2 ............ 21 3.2 Multiplication Table for basis blades in C`3 ............ 22 3.3 The dot product of a bivector and a vector ............ 24 4.1 Projection and rejection of vector a in bivector B ......... 32 4.2 Reflection ............................... 35 4.3 The Meet ............................... 36 5.1 Lines in the Euclidian plane ..................... 42 5.2 Rotation in an arbitrary plane ................... 44 5.3 An arbitrary rotation ......................... 48 5.4 A rotation using two reflections ................... 51 5.5 A two dimensional line in the homogeneous model ........ 56 5.6 An homogeneous intersection .................... 57 3 Chapter 1 Introduction 1.1 Rationale Information about geometric algebra is widely available in the field of physics. Knowledge applicable to computer science, graphics in particular, is lacking. As Leo Dorst [1] puts it: “. A computer scientist first pointed to geometric algebra as a promising way to ‘do geometry’ is likely to find a rather confusing collection of material, of which very little is experienced as imme- diately relevant to the kind of geometrical problems occurring in practice. After perusing some of these, the computer scientist may well wonder what all the fuss is about, and decide to stick with the old way of doing things . ” And indeed, disappointed by the mathematical obscurity many people dis- card geometric algebra as something for academics only. Unfortunately they miss out on the elegance and power that geometric algebra has to offer. Not only does geometric algebra provide us with new ways to reason about computational geometry, it also embeds and explains all existing theories in- cluding complex numbers, quaternions, matrix-algebra, and Pl¨uckerspace. Geo- metric algebra gives us the necessary and unifying tools to express geometry and its relations without the need for tricks or special cases. Ultimately, it makes communicating ideas easier. 1.2 Overview The layout of the paper is as follows; I start out by talking a bit about sub- spaces, what they are, what we can do with them and how traditional vectors or one-dimensional subspaces fit in the picture. After that I will define what a 4 geometric algebra is, and what the fundamental concepts are. This chapter is the most important as all other theory builds upon it. The following chapter will introduce some common and handy concepts which I call tools. They are not fundamental, but useful in many applications. Once we have mastered the fundamentals, and armed with our tools, we can tackle some applications of geometric algebra. It is this chapter that tries to demonstrate the elegance of geometric algebra, and how and where it replaces traditional methods. Finally, I wrap things up, and provide a few references and a roadmap on how to continue a study of geometric algebra.. 1.3 Acknowledgements I would like to thank David Hestenes for his books [7][8] and papers [10] and Leo Dorst for the papers on his website [6]. Anything you learn from this introduction, you indirectly learned from them. My gratitude to Per Vognsen for explaining many of the mathematical ob- scurities that I encountered, and providing me with some of the proofs in this paper. Thanks to Kurt Miller, Conor Stokes, Patrick Harty, Matt Newport, Willem De Boer, Frank A. Krueger and Robert Valkenburg for comments. Fi- nally, I am greatly indebted to Dirk Gerrits. His excellent skills as an editor and his thorough proofreading allowed me to correct many errors. 1.4 Disclaimer Of course, any mistakes in this text are entirely mine. I only hope to provide an easy-to-read introduction. Proofs will be omitted if the required mathematics are beyond the scope of this paper. Many times only an example or an intuitive outline will be given. I am certain that some of my reasoning won’t hold in a thorough mathematical review, but at least you should get an impression. The enthusiastic reader should pick up some of the references to extend his knowledge, learn about some of the subtleties and find the actual proofs. 5 Chapter 2 Subspaces It is often neglected that vectors represent 1-dimensional subspaces. This is mainly due to the fact that it seems the only concept at hand. Hence we abuse vectors to form higher-dimensional subspaces. We use them to represent planes by defining normals. We combine them in strange ways to create oriented subspaces. Some papers even mention quaternions as vectors on a 4-dimensional unit hypersphere. For no apparent reason we have been denying the existence of 2-, 3- and higher-dimensional subspaces as simple concepts, similar to the vector. Ge- ometric algebra introduces these and even defines the operators to perform arithmetic with them. Using geometric algebra we can finally represent planes as true 2-dimensional subspaces, define oriented subspaces, and reveal the true identity of quaternions. We can add and subtract subspaces of different dimen- sions, and even multiply and divide them, resulting in powerful expressions that can express any geometric relation or concept. This chapter will demonstrate how vectors represent 1-dimensional subspaces and uses this knowledge to express subspaces of arbitrary dimensions. However, before we get to that, let us consider the very basics by using a familiar example. a b Figure 2.1: The dot product What if we project a 1-dimensional subspace onto another? The answer is well known; For vectors a and b, the dot product a ¢ b projects a onto b resulting in the scalar magnitude of the projection relative to b’s magnitude. This is 6 depicted in figure 2.1 for the case where b is a unit vector. Scalars can be treated as 0-dimensional subspaces. Thus, the projection of a 1-dimensional subspace onto another results in a 0-dimensional subspace. 2.1 Bivectors Geometric algebra introduces an operator that is in some ways
Load more

Recommended publications
  • 21. Orthonormal Bases
    21. Orthonormal Bases The canonical/standard basis 011 001 001 B C B C B C B0C B1C B0C e1 = B.C ; e2 = B.C ; : : : ; en = B.C B.C B.C B.C @.A @.A @.A 0 0 1 has many useful properties. • Each of the standard basis vectors has unit length: q p T jjeijj = ei ei = ei ei = 1: • The standard basis vectors are orthogonal (in other words, at right angles or perpendicular). T ei ej = ei ej = 0 when i 6= j This is summarized by ( 1 i = j eT e = δ = ; i j ij 0 i 6= j where δij is the Kronecker delta. Notice that the Kronecker delta gives the entries of the identity matrix. Given column vectors v and w, we have seen that the dot product v w is the same as the matrix multiplication vT w. This is the inner product on n T R . We can also form the outer product vw , which gives a square matrix. 1 The outer product on the standard basis vectors is interesting. Set T Π1 = e1e1 011 B C B0C = B.C 1 0 ::: 0 B.C @.A 0 01 0 ::: 01 B C B0 0 ::: 0C = B. .C B. .C @. .A 0 0 ::: 0 . T Πn = enen 001 B C B0C = B.C 0 0 ::: 1 B.C @.A 1 00 0 ::: 01 B C B0 0 ::: 0C = B. .C B. .C @. .A 0 0 ::: 1 In short, Πi is the diagonal square matrix with a 1 in the ith diagonal position and zeros everywhere else.
    [Show full text]
  • Glossary of Linear Algebra Terms
    INNER PRODUCT SPACES AND THE GRAM-SCHMIDT PROCESS A. HAVENS 1. The Dot Product and Orthogonality 1.1. Review of the Dot Product. We first recall the notion of the dot product, which gives us a familiar example of an inner product structure on the real vector spaces Rn. This product is connected to the Euclidean geometry of Rn, via lengths and angles measured in Rn. Later, we will introduce inner product spaces in general, and use their structure to define general notions of length and angle on other vector spaces. Definition 1.1. The dot product of real n-vectors in the Euclidean vector space Rn is the scalar product · : Rn × Rn ! R given by the rule n n ! n X X X (u; v) = uiei; viei 7! uivi : i=1 i=1 i n Here BS := (e1;:::; en) is the standard basis of R . With respect to our conventions on basis and matrix multiplication, we may also express the dot product as the matrix-vector product 2 3 v1 6 7 t î ó 6 . 7 u v = u1 : : : un 6 . 7 : 4 5 vn It is a good exercise to verify the following proposition. Proposition 1.1. Let u; v; w 2 Rn be any real n-vectors, and s; t 2 R be any scalars. The Euclidean dot product (u; v) 7! u · v satisfies the following properties. (i:) The dot product is symmetric: u · v = v · u. (ii:) The dot product is bilinear: • (su) · v = s(u · v) = u · (sv), • (u + v) · w = u · w + v · w.
    [Show full text]
  • A Some Basic Rules of Tensor Calculus
    A Some Basic Rules of Tensor Calculus The tensor calculus is a powerful tool for the description of the fundamentals in con- tinuum mechanics and the derivation of the governing equations for applied prob- lems. In general, there are two possibilities for the representation of the tensors and the tensorial equations: – the direct (symbolic) notation and – the index (component) notation The direct notation operates with scalars, vectors and tensors as physical objects defined in the three dimensional space. A vector (first rank tensor) a is considered as a directed line segment rather than a triple of numbers (coordinates). A second rank tensor A is any finite sum of ordered vector pairs A = a b + ... +c d. The scalars, vectors and tensors are handled as invariant (independent⊗ from the choice⊗ of the coordinate system) objects. This is the reason for the use of the direct notation in the modern literature of mechanics and rheology, e.g. [29, 32, 49, 123, 131, 199, 246, 313, 334] among others. The index notation deals with components or coordinates of vectors and tensors. For a selected basis, e.g. gi, i = 1, 2, 3 one can write a = aig , A = aibj + ... + cidj g g i i ⊗ j Here the Einstein’s summation convention is used: in one expression the twice re- peated indices are summed up from 1 to 3, e.g. 3 3 k k ik ik a gk ∑ a gk, A bk ∑ A bk ≡ k=1 ≡ k=1 In the above examples k is a so-called dummy index. Within the index notation the basic operations with tensors are defined with respect to their coordinates, e.
    [Show full text]
  • The Dot Product
    The Dot Product In this section, we will now concentrate on the vector operation called the dot product. The dot product of two vectors will produce a scalar instead of a vector as in the other operations that we examined in the previous section. The dot product is equal to the sum of the product of the horizontal components and the product of the vertical components. If v = a1 i + b1 j and w = a2 i + b2 j are vectors then their dot product is given by: v · w = a1 a2 + b1 b2 Properties of the Dot Product If u, v, and w are vectors and c is a scalar then: u · v = v · u u · (v + w) = u · v + u · w 0 · v = 0 v · v = || v || 2 (cu) · v = c(u · v) = u · (cv) Example 1: If v = 5i + 2j and w = 3i – 7j then find v · w. Solution: v · w = a1 a2 + b1 b2 v · w = (5)(3) + (2)(-7) v · w = 15 – 14 v · w = 1 Example 2: If u = –i + 3j, v = 7i – 4j and w = 2i + j then find (3u) · (v + w). Solution: Find 3u 3u = 3(–i + 3j) 3u = –3i + 9j Find v + w v + w = (7i – 4j) + (2i + j) v + w = (7 + 2) i + (–4 + 1) j v + w = 9i – 3j Example 2 (Continued): Find the dot product between (3u) and (v + w) (3u) · (v + w) = (–3i + 9j) · (9i – 3j) (3u) · (v + w) = (–3)(9) + (9)(-3) (3u) · (v + w) = –27 – 27 (3u) · (v + w) = –54 An alternate formula for the dot product is available by using the angle between the two vectors.
    [Show full text]
  • Concept of a Dyad and Dyadic: Consider Two Vectors a and B Dyad: It Consists of a Pair of Vectors a B for Two Vectors a a N D B
    1/11/2010 CHAPTER 1 Introductory Concepts • Elements of Vector Analysis • Newton’s Laws • Units • The basis of Newtonian Mechanics • D’Alembert’s Principle 1 Science of Mechanics: It is concerned with the motion of material bodies. • Bodies have different scales: Microscropic, macroscopic and astronomic scales. In mechanics - mostly macroscopic bodies are considered. • Speed of motion - serves as another important variable - small and high (approaching speed of light). 2 1 1/11/2010 • In Newtonian mechanics - study motion of bodies much bigger than particles at atomic scale, and moving at relative motions (speeds) much smaller than the speed of light. • Two general approaches: – Vectorial dynamics: uses Newton’s laws to write the equations of motion of a system, motion is described in physical coordinates and their derivatives; – Analytical dynamics: uses energy like quantities to define the equations of motion, uses the generalized coordinates to describe motion. 3 1.1 Vector Analysis: • Scalars, vectors, tensors: – Scalar: It is a quantity expressible by a single real number. Examples include: mass, time, temperature, energy, etc. – Vector: It is a quantity which needs both direction and magnitude for complete specification. – Actually (mathematically), it must also have certain transformation properties. 4 2 1/11/2010 These properties are: vector magnitude remains unchanged under rotation of axes. ex: force, moment of a force, velocity, acceleration, etc. – geometrically, vectors are shown or depicted as directed line segments of proper magnitude and direction. 5 e (unit vector) A A = A e – if we use a coordinate system, we define a basis set (iˆ , ˆj , k ˆ ): we can write A = Axi + Ay j + Azk Z or, we can also use the A three components and Y define X T {A}={Ax,Ay,Az} 6 3 1/11/2010 – The three components Ax , Ay , Az can be used as 3-dimensional vector elements to specify the vector.
    [Show full text]
  • Derivation of the Two-Dimensional Dot Product
    Derivation of the two-dimensional dot product Content 1. Motivation ....................................................................................................................................... 1 2. Derivation of the dot product in R2 ................................................................................................. 1 2.1. Area of a rectangle ...................................................................................................................... 2 2.2. Area of a right-angled triangle .................................................................................................... 2 2.3. Pythagorean Theorem ................................................................................................................. 2 2.4. Area of a general triangle using the law of cosines ..................................................................... 3 2.5. Derivation of the dot product from the law of cosines ............................................................... 5 3. Geometric Interpretation ................................................................................................................ 5 3.1. Basics ........................................................................................................................................... 5 3.2. Projection .................................................................................................................................... 6 4. Summary.........................................................................................................................................
    [Show full text]
  • Tropical Arithmetics and Dot Product Representations of Graphs
    Utah State University DigitalCommons@USU All Graduate Theses and Dissertations Graduate Studies 5-2015 Tropical Arithmetics and Dot Product Representations of Graphs Nicole Turner Utah State University Follow this and additional works at: https://digitalcommons.usu.edu/etd Part of the Mathematics Commons Recommended Citation Turner, Nicole, "Tropical Arithmetics and Dot Product Representations of Graphs" (2015). All Graduate Theses and Dissertations. 4460. https://digitalcommons.usu.edu/etd/4460 This Thesis is brought to you for free and open access by the Graduate Studies at DigitalCommons@USU. It has been accepted for inclusion in All Graduate Theses and Dissertations by an authorized administrator of DigitalCommons@USU. For more information, please contact [email protected]. TROPICAL ARITHMETICS AND DOT PRODUCT REPRESENTATIONS OF GRAPHS by Nicole Turner A thesis submitted in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE in Mathematics Approved: David E. Brown Brynja Kohler Major Professor Committee Member LeRoy Beasley Mark McLellan Committee Member Vice President for Research Dean of the School of Graduate Studies UTAH STATE UNIVERSITY Logan, Utah 2015 ii Copyright c Nicole Turner 2015 All Rights Reserved iii ABSTRACT Tropical Arithmetics and Dot Product Representations of Graphs by Nicole Turner, Master of Science Utah State University, 2015 Major Professor: Dr. David Brown Department: Mathematics and Statistics A dot product representation (DPR) of a graph is a function that maps each vertex to a vector and two vertices are adjacent if and only if the dot product of their function values is greater than a given threshold. A tropical algebra is the antinegative semiring on IR[f1; −∞} with either minfa; bg replacing a+b and a+b replacing a·b (min-plus), or maxfa; bg replacing a + b and a + b replacing a · b (max-plus), and the symbol 1 is the additive identity in min-plus while −∞ is the additive identity in max-plus; the multiplicative identity is 0 in min-plus and in max-plus.
    [Show full text]
  • Inner Product Spaces
    CHAPTER 6 Woman teaching geometry, from a fourteenth-century edition of Euclid’s geometry book. Inner Product Spaces In making the definition of a vector space, we generalized the linear structure (addition and scalar multiplication) of R2 and R3. We ignored other important features, such as the notions of length and angle. These ideas are embedded in the concept we now investigate, inner products. Our standing assumptions are as follows: 6.1 Notation F, V F denotes R or C. V denotes a vector space over F. LEARNING OBJECTIVES FOR THIS CHAPTER Cauchy–Schwarz Inequality Gram–Schmidt Procedure linear functionals on inner product spaces calculating minimum distance to a subspace Linear Algebra Done Right, third edition, by Sheldon Axler 164 CHAPTER 6 Inner Product Spaces 6.A Inner Products and Norms Inner Products To motivate the concept of inner prod- 2 3 x1 , x 2 uct, think of vectors in R and R as x arrows with initial point at the origin. x R2 R3 H L The length of a vector in or is called the norm of x, denoted x . 2 k k Thus for x .x1; x2/ R , we have The length of this vector x is p D2 2 2 x x1 x2 . p 2 2 x1 x2 . k k D C 3 C Similarly, if x .x1; x2; x3/ R , p 2D 2 2 2 then x x1 x2 x3 . k k D C C Even though we cannot draw pictures in higher dimensions, the gener- n n alization to R is obvious: we define the norm of x .x1; : : : ; xn/ R D 2 by p 2 2 x x1 xn : k k D C C The norm is not linear on Rn.
    [Show full text]
  • 1 Vectors & Tensors
    1 Vectors & Tensors The mathematical modeling of the physical world requires knowledge of quite a few different mathematics subjects, such as Calculus, Differential Equations and Linear Algebra. These topics are usually encountered in fundamental mathematics courses. However, in a more thorough and in-depth treatment of mechanics, it is essential to describe the physical world using the concept of the tensor, and so we begin this book with a comprehensive chapter on the tensor. The chapter is divided into three parts. The first part covers vectors (§1.1-1.7). The second part is concerned with second, and higher-order, tensors (§1.8-1.15). The second part covers much of the same ground as done in the first part, mainly generalizing the vector concepts and expressions to tensors. The final part (§1.16-1.19) (not required in the vast majority of applications) is concerned with generalizing the earlier work to curvilinear coordinate systems. The first part comprises basic vector algebra, such as the dot product and the cross product; the mathematics of how the components of a vector transform between different coordinate systems; the symbolic, index and matrix notations for vectors; the differentiation of vectors, including the gradient, the divergence and the curl; the integration of vectors, including line, double, surface and volume integrals, and the integral theorems. The second part comprises the definition of the tensor (and a re-definition of the vector); dyads and dyadics; the manipulation of tensors; properties of tensors, such as the trace, transpose, norm, determinant and principal values; special tensors, such as the spherical, identity and orthogonal tensors; the transformation of tensor components between different coordinate systems; the calculus of tensors, including the gradient of vectors and higher order tensors and the divergence of higher order tensors and special fourth order tensors.
    [Show full text]
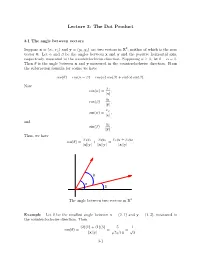
  • The Dot Product
    Lecture 3: The Dot Product 3.1 The angle between vectors 2 Suppose x = (x1; x2) and y = (y1; y2) are two vectors in R , neither of which is the zero vector 0. Let α and β be the angles between x and y and the positive horizontal axis, respectively, measured in the counterclockwise direction. Supposing α β, let θ = α β. Then θ is the angle between x and y measured in the counterclockwise≥ direction. From− the subtraction formula for cosine we have cos(θ) = cos(α β) = cos(α) cos(β) + sin(α) sin(β): − Now x cos(α) = 1 ; x j j y cos(β) = 1 ; y j j x sin(α) = 2 ; x j j and y sin(β) = 2 : y j j Thus, we have x y x y x y + x y cos(θ) = 1 1 + 2 2 = 1 1 2 2 : x y x y x y j jj j j jj j j jj j θ α β The angle between two vectors in R2 Example Let θ be the smallest angle between x = (2; 1) and y = (1; 3), measured in the counterclockwise direction. Then (2)(1) + (1)(3) 5 1 cos(θ) = = = : x y p5p10 p2 j jj j 3-1 Lecture 3: The Dot Product 3-2 Hence 1 1 π θ = cos− = : p2 4 With more work it is possible to show that if x = (x1; x2; x3) and y = (y1; y2; y3) are two vectors in R3, neither of which is the zero vector 0, and θ is the smallest positive angle between x and y, then x y + x y + x y cos(θ) = 1 1 2 2 3 3 x y j jj j 3.2 The dot product n Definition If x = (x1; x2; : : : ; xn) and y = (y1; y2; : : : ; yn) are vectors in R , then the dot product of x and y, denoted x y, is given by · x y = x1y1 + x2y2 + + xnyn: · ··· Note that the dot product of two vectors is a scalar, not another vector.
    [Show full text]
  • 16 the Transpose
    The Transpose Learning Goals: to expose some properties of the transpose We would like to see what happens with our factorization if we get zeroes in the pivot positions and have to employ row exchanges. To do this we need to look at permutation matrices. But to study these effectively, we need to know something about the transpose. So the transpose of a matrix is what you get by swapping rows for columns. In symbols, T ⎡2 −1⎤ T ⎡ 2 0 4⎤ ⎢ ⎥ A ij = Aji. By example, ⎢ ⎥ = 0 3 . ⎣−1 3 5⎦ ⎢ ⎥ ⎣⎢4 5 ⎦⎥ Let’s take a look at how the transpose interacts with algebra: T T T T • (A + B) = A + B . This is simple in symbols because (A + B) ij = (A + B)ji = Aji + Bji = Y T T T A ij + B ij = (A + B )ij. In practical terms, it just doesn’t matter if we add first and then flip or flip first and then add • (AB)T = BTAT. We can do this in symbols, but it really doesn’t help explain why this is n true: (AB)T = (AB) = T T = (BTAT) . To get a better idea of what is ij ji ∑a jkbki = ∑b ika kj ij k =1 really going on, look at what happens if B is a single column b. Then Ab is a combination of the columns of A. If we transpose this, we get a row which is a combination of the rows of AT. In other words, (Ab)T = bTAT. Then we get the whole picture of (AB)T by placing several columns side-by-side, which is putting a whole bunch of rows on top of each other in BT.
    [Show full text]
  • VISUALIZING EXTERIOR CALCULUS Contents Introduction 1 1. Exterior
    VISUALIZING EXTERIOR CALCULUS GREGORY BIXLER Abstract. Exterior calculus, broadly, is the structure of differential forms. These are usually presented algebraically, or as computational tools to simplify Stokes' Theorem. But geometric objects like forms should be visualized! Here, I present visualizations of forms that attempt to capture their geometry. Contents Introduction 1 1. Exterior algebra 2 1.1. Vectors and dual vectors 2 1.2. The wedge of two vectors 3 1.3. Defining the exterior algebra 4 1.4. The wedge of two dual vectors 5 1.5. R3 has no mixed wedges 6 1.6. Interior multiplication 7 2. Integration 8 2.1. Differential forms 9 2.2. Visualizing differential forms 9 2.3. Integrating differential forms over manifolds 9 3. Differentiation 11 3.1. Exterior Derivative 11 3.2. Visualizing the exterior derivative 13 3.3. Closed and exact forms 14 3.4. Future work: Lie derivative 15 Acknowledgments 16 References 16 Introduction What's the natural way to integrate over a smooth manifold? Well, a k-dimensional manifold is (locally) parametrized by k coordinate functions. At each point we get k tangent vectors, which together form an infinitesimal k-dimensional volume ele- ment. And how should we measure this element? It seems reasonable to ask for a function f taking k vectors, so that • f is linear in each vector • f is zero for degenerate elements (i.e. when vectors are linearly dependent) • f is smooth These are the properties of a differential form. 1 2 GREGORY BIXLER Introducing structure to a manifold usually follows a certain pattern: • Create it in Rn.
    [Show full text]